A Book of Abstract Algebra, Second Edition (1982)
Chapter 14. HOMOMORPHISMS
We have seen that if two groups are isomorphic, this means there is a one-to-one correspondence between them which transforms one of the groups into the other. Now if G and H are any groups, it may happen that there is a function which transforms G into H, although this function is not a one-to-one correspondence. For example, ![]() 6 is transformed into
6 is transformed into ![]() 3 by
3 by
![]()
as we may verify by comparing their tables:

If G and H are any groups, and there is a function f which transforms G into H, we say that if is a homomorphic image of G. The function f is called a homomorphism from G to f. This notion of homomorphism is one of the skeleton keys of algebra, and this chapter is devoted to explaining it and defining it precisely.
First, let us examine carefully what we mean by saying that “f transforms G into H.” To begin with, f must be a function from G onto H; but that is not all, because f must also transform the table of G into the table of H. To accomplish this, f must have the following property: for any two elements a and b in G,
if f(a) = a′ and f(b) = b′, then f(ab) = a′ b′ (1)
Graphically,
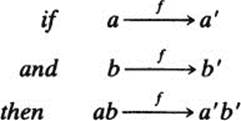
Condition (1) may be written more succinctly as follows:
f(ab) = f(a)f(b) (2)
Thus,
Definition if G and H are groups, a homomorphism from G to H is a function f: G →H such that for any two elements a and b in G,
f(ab) = f(a)f(b)
If there exists a homomorphism from G onto H, we say that H is a homomorphic image of G.
Groups have a very important and privileged relationship with their homomorphic images, as the next few examples will show.
Let P denote the group consisting of two elements, e and o, with the table
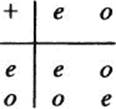
We call this group the parity group of even and odd numbers. We should think of e as “even” and o as “odd,” and the table as describing the rule for adding even and odd numbers. For example, even + odd = odd, odd + odd = even, and so on.
The function f: ![]() →P which carries every even integer to e and every odd integer to o is clearly a homomorphism from
→P which carries every even integer to e and every odd integer to o is clearly a homomorphism from ![]() to P. This is easy to check because there are only four different cases: for arbitrary integers r and s, r and s are either both even, both odd, or mixed. For example, if r and s are both odd, their sum is even, so f(r) = 0, f(s) = o, and f(r + s) = e. Since e = o + o,
to P. This is easy to check because there are only four different cases: for arbitrary integers r and s, r and s are either both even, both odd, or mixed. For example, if r and s are both odd, their sum is even, so f(r) = 0, f(s) = o, and f(r + s) = e. Since e = o + o,
f(r+ s) = f(r)+f(s)
This equation holds analogously in the remaining three cases; hence f is a homomorphism. (Note that the symbol + is used on both sides of the above equation because the operation, in ![]() as well as in P, is denoted by +.)
as well as in P, is denoted by +.)
It follows that P is a homomorphic image of ![]() !
!
Now, what do P and ![]() have in common? P is a much smaller group than
have in common? P is a much smaller group than ![]() , therefore it is not surprising that very few properties of the integers are to be found in P. Nevertheless, one aspect of the structure of
, therefore it is not surprising that very few properties of the integers are to be found in P. Nevertheless, one aspect of the structure of ![]() is retained absolutely intact in P, namely, the structure of the odd and even numbers. (The fact of being odd or even is called the parity of integers.) In other words, as we pass from
is retained absolutely intact in P, namely, the structure of the odd and even numbers. (The fact of being odd or even is called the parity of integers.) In other words, as we pass from ![]() to P we deliberately lose every aspect of the integers except their parity ; their parity alone (with its arithmetic) is retained, and faithfully preserved.
to P we deliberately lose every aspect of the integers except their parity ; their parity alone (with its arithmetic) is retained, and faithfully preserved.
Another example will make this point clearer. Remember that D4 is the group of the symmetries of the square. Now, every symmetry of the
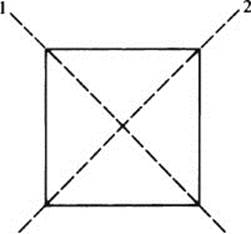
square either interchanges the two diagonals here labeled 1 and 2, or leaves them as they were. In other words, every symmetry of the square brings about one of the permutations
![]()
of the diagonals.
For each Ri ∈ D4, let f(Ri) be the permutation of the diagonals produced by Ri Then f is clearly a homomorphism from D4 onto S2. Indeed, it is clear on geometrical grounds that when we perform the motion Ri followed by the motion Rj on the square, we are, at the same time, carrying out the motions f(Ri) followed by f(Rj) on the diagonals. Thus,
f(RjºRi) = f(Rj)ºf(Ri)
It follows that 52 is a homomorphic image of D4. Now S2 is a smaller group than D4, and therefore very few of the features of D4 are to be found in S2. Nevertheless, one aspect of the structure of D4 is retained absolutely intact in S2, namely, the diagonal motions. Thus, as we pass from D4 to 52, we deliberately lose every aspect of plane motions except the motions of the diagonals; these alone are retained and faithfully preserved.
A final example may be of some help; it relates to the group ![]() described in Chapter 3, Exercise E. Here, briefly, is the context in which this group arises: The most basic way of transmitting information is to code it into strings of Os and Is, such as 0010111, 1010011, etc. Such strings are called binary words, and the number of 0s and Is in any binary word is called its length. The symbol
described in Chapter 3, Exercise E. Here, briefly, is the context in which this group arises: The most basic way of transmitting information is to code it into strings of Os and Is, such as 0010111, 1010011, etc. Such strings are called binary words, and the number of 0s and Is in any binary word is called its length. The symbol ![]() designates the group consisting of all binary words of length n, with an operation of addition described in Chapter 3, Exercise E.
designates the group consisting of all binary words of length n, with an operation of addition described in Chapter 3, Exercise E.
Consider the function f: ![]() →
→![]() which consists of dropping the last two digits of every seven-digit word. This kind of function arises in many practical situations: for example, it frequently happens that the first five digits of a word carry the message while the last two digits are an error check. Thus, f separates the message from the error check.
which consists of dropping the last two digits of every seven-digit word. This kind of function arises in many practical situations: for example, it frequently happens that the first five digits of a word carry the message while the last two digits are an error check. Thus, f separates the message from the error check.
It is easy to verify that f is a homomorphism; hence ![]() is a homomorphic image of
is a homomorphic image of ![]() . As we pass from
. As we pass from ![]() to
to ![]() , the message component of words in
, the message component of words in ![]() is exactly preserved while the error check is deliberately lost.
is exactly preserved while the error check is deliberately lost.
These examples illustrate the basic idea inherent in the concept of a homomorphic image. The cases which arise in practice are not always so clear-cut as these, but the underlying idea is still the same: In a homomorphic image of G, some aspect of G is isolated and faithfully preserved while all else is deliberately lost.
The next theorem presents two eleirientary properties of homomorphisms.
Theorem 1 Let G and H be groups, and f: G → H a homomorphism. Then
(i)f(e) = e, and
(ii)f(a−l) = [f(a)]−l for every element a ∈ G.
In the equation f(e) = e, the letter e on the left refers to the neutral element in G, whereas the letter e on the right refers to the neutral element in H.
To prove (i), we note that in any group,
ifyy = y then y = e
(Use the cancellation law on the equation yy = ye.) Now, f(e)f(e) = f(ee) = f(e); hence f(e) = e.
To prove (ii), note that f(a)f(a−1) = f(aa−1) = f(e). But f(e) = e, so f(a)f(a−1) = e. It follows by Theorem 2 of Chapter 4 that f(a−1) is the inverse of f(a), that is, f(a−l) = [f(a)]−1.
Before going on with our study of homomorphisms, we must be introduced to an important new concept. If a is an element of a group G, a conjugate of α is any element of the form xax−l, where x ∈G. For example, the conjugates of α in S3 are
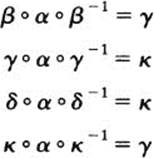
as well as a itself, which may be written in two ways, as ε ∘ α ∘ ε −1 or as α ∘ α ∘ α −1. if H is any subset of a group G, we say that H is closed with respect to conjugates if every conjugate of every element of H is in H. Finally,
Definition Let H be a subgroup of a group G. H is called a normal subgroup of G if it is closed with respect to conjugates, that is, if
for anya ∈ Handx ∈ G xax−l ∈ H
(Note that according to this definition, a normal subgroup of G is any nonempty subset of G which is closed with respect to products, with respect to inverses, and with respect to conjugates.)
We now return to our discussion of homomorphisms.
Definition Let f : G → H be a homomorphism. The kernel of f is the set K of all the elements of G which are carried by f onto the neutral element of H. That is,
K = {x ∈ G: f(x) = e}
Theorem 2 Let f : G → H be a homomorphism.
(i)The kernel of f is a normal subgroup of G, and
(ii)The range of f is a subgroup of H.
PROOF: Let K denote the kernel of f. If a, b ∈ K, this means that f(a) = e and f(b) = e. Thus, f(ab) = f(a)f(b) = ee = e; hence ab ∈ k.
If a ∈ k, then f(a) = e. Thus, f(a−l) = [f(a)]−1 = e−1 = e, so a−1 ∈ K.
Finally, if a − K and x ∈ G, then f(xax−l) = f(x)f(a)f(x−l) = f(x)f(a)[f(x)]−1 = e, which shows that xax−l ∈ K. Thus, K is a normal subgroup of G.
Now we must prove part (ii). If f(a) and f(b) are in the range of f, then their product f(a)f(b) =f(ab) is also in the range of f.
If f(a) is in the range of f, its inverse is [f(a)]−l = f(a−l), which is also in the range of f. Thus, the range of f is a subgroup of H. ■
If f is a homomorphism, we represent the kernel of f and the range of f with the symbols
ker(f)andran(f)
EXERCISES
A. Examples of Homomorphisms of Finite Groups
1 Consider the function f : ![]() 8 →
8 → ![]() 4 given by
4 given by
![]()
Verify that f is a homomorphism, find its kernel K, and list the cosets of K. [REMARK: To verify that f is a homomorphism, you must show that f(a + b) = f(a) + f(b) for all choices of a and b in ![]() 8; there are 64 choices. This may be accomplished by checking that f transforms the table of
8; there are 64 choices. This may be accomplished by checking that f transforms the table of ![]() 8 to the table of
8 to the table of ![]() 4, as on page 136.]
4, as on page 136.]
2 Consider the function f : S3 → ![]() 2 given by
2 given by
![]()
Verify that f is a homomorphism, find its kernel K, and list the cosets of K.
3 Find a homomorphism f:![]() 15 →
15 → ![]() 5, and indicate its kernel. (Do not actually verify that f is a homomorphism.)
5, and indicate its kernel. (Do not actually verify that f is a homomorphism.)
4 Imagine a square as a piece of paper lying on a table. The side facing you is side

A. The side hidden from view is side B. Every motion of the square either interchanges the two sides (that is, side B becomes visible and side A hidden) or leaves the sides as they were. In other words, every motion Ri of the square brings about one of the permutations
![]()
of the sides; call it g(Ri). Verify that g: D4 ![]() S2 is a homomorphism, and give its kernel.
S2 is a homomorphism, and give its kernel.
5 Every motion of the regular hexagon brings about a permutation of its diagonals, labeled 1, 2, and 3. For each Ri ∈ D6, let f(Ri) be the permutation of
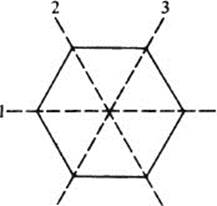
the diagonals produced by Ri Argue informally (appealing to geometric intuition) to explain why f: D6∈ S3 is a homomorphism. Then complete the following:
![]()
(That is, find the value of f on all 12 elements of D6.)
# 6 Let B ⊂ A. Let h : PA → PB be defined by h(C) = C = C ![]() B. For A = {1,2,3} and B = {1, 2}, complete the following:
B. For A = {1,2,3} and B = {1, 2}, complete the following:
![]()
For any A and B ⊂ A, show that h is a homomorphism.
B. Examples of Homomorphisms of Infinite Groups
Prove that each of the following is a homomorphism, and describe its kernel.
1 The function ϕ : ![]() (
(![]() )→
)→ ![]() given by ϕ(f) = f(0).
given by ϕ(f) = f(0).
2 The function ϕ : ![]() (
(![]() ) →
) → ![]() (
(![]() ) given by ϕ(f) = f ′.
) given by ϕ(f) = f ′. ![]() (R) is the group of differentiable functions from
(R) is the group of differentiable functions from ![]() to
to ![]() f′ is the derivative of f.
f′ is the derivative of f.
3 The function f:![]() ×
× ![]() →
→ ![]() given by f(x, y) = x + y.
given by f(x, y) = x + y.
4 The function f :![]() * →
* → ![]() pos defined by f(x) = |x|.
pos defined by f(x) = |x|.
5 The function f : ![]() * →
* → ![]() pos defined by f(a + bi) =
pos defined by f(a + bi) = ![]() .
.
6 Let G be the multiplicative group of all 2 × 2 matrices
![]()
satisfying ad − bc ≠ 0. Let f: G → ![]() * be given by f(A) = determinant of A = ad − bc.
* be given by f(A) = determinant of A = ad − bc.
C. Elementary Properties of Homomorphisms
Let G, H, and K be groups. Prove the following:
1 If f : G → G and g :H →K are homomorphisms, then their composite gº f: G→ K is a homomorphism.
# 2 If f : G → H is a homomorphism with kernel K, then f is injective iff K = {e}.
3 If f : G → H is a homomorphism and is any subgroup of G, then f(K) = {f(x) : x ∈ K} is a subgroup of H.
4 If f : G → H is a homomorphism and j is any subgroup of H, then
f−1(J) = {x ∈G: f(x)∈J}
is a subgroup of G. Furthermore, ker f ⊆ f−1(J).
5 If f : G → H is a homomorphism with kernel K, and J is a subgroup of G, letfJ designate the restriction of f to J. (In other words fJ is the same function as f, except that its domain is restricted to J.) Then ker fJ = J ![]() K.
K.
6 For any group G, the function f: G → G defined by f(x) = e is a homomorphism.
7 For any group G, {e} and G are homomorphic images of G.
8 The function f: G→G defined by f(x) = x2 is a homomorphism iff G is abelian.
9 The functions f1(x, y) = x and f2(x, y) = y, from G × H to G and H, respectively, are homomorphisms.
D. Basic Properties of Normal Subgroups
In the following, let G denote an arbitrary group.
1 Find all the normal subgroups (a) of S3 and (b) of D4.
Prove the following:
2 Every subgroup of an abelian group is normal.
3 The center of any group G is a normal subgroup of G.
4 Let H be a subgroup of G. H is normal iff it has the following property: For all a and b in G, ab ∈ H iff ba ∈ H.
5 Let H be a subgroup of G. H is normal iff aH = Ha for every a ∈ G.
6 Any intersection of normal subgroups of G is a normal subgroup of G.
E. Further Properties of Normal Subgroups
Let G denote a group, and H a subgroup of G. Prove the following:
# 1 If H has index 2 in G, then H is normal. (HINT: Use Exercise D5.)
2 Suppose an element a ∈ G has order 2. Then (⟨a⟩) is a normal subgroup of G iff a is in the center of G.
3 If a is any element of G, (⟨a⟩) is a normal subgroup of G iff a has the following property: For any x ∈ G, there is a positive integer k such that xa = akx.
4 In a group G, a commutator is any product of the form aba−1b−1, where a and b are any elements of G. If a subgroup H of G contains all the commutators of G, then H is normal.
5 If H and K are subgroups of G, and K is normal, then HK is a subgroup of G. (HK denotes the set of all products hk as h ranges over H and k ranges over K.)
# 6 Let S be the union of all the cosets Ha such that Ha = aH. Then S is a subgroup of G, and H is a normal subgroup of S.
F. Homomorphism and the Order of Elements
If f : G → H is a homomorphism, prove each of the following:
1 For each element a ∈G, the order of f(a) is a divisor of the order of a.
2 The order of any element b ≠ e in the range of f is a common divisor of |G| and |H|. (Use part 1.)
3 If the range of f has n elements, then xn ∈ ker f for every x ∈ G.
4 Let m be an integer such that m and |H| are relatively prime. For any x ∈ G, if xm ∈ ker f, then x ∈ ker f.
5 Let the range of f have m elements. If a ∈ G has order n, where m and n are relatively prime, then a is in the kernel of f. (Use part 1.)
6 Let p be a prime. If ran f has an element of order p, then G has an element of order p.
G. Properties Preserved under Homomorphism
A property of groups is said to be “preserved under homomorphism” if, whenever a group G has that property, every homomorphic image of G does also. In this exercise set, we will survey a few typical properties preserved under homomorphism. If f : G → H is a homomorphism of G onto H, prove each of the following:
1 If G is abelian, then H is abelian.
2 If G is cyclic, then H is cyclic.
3 If every element of G has finite order, then every element of H has finite order.
4 If every element of G is its own inverse, every element of H is its own inverse.
5 If every element of G has a square root, then every element of H has a square root.
6 If G is finitely generated, then H is finitely generated. (A group is said to be “finitely generated” if it is generated by finitely many of its elements.)
† H. Inner Direct Products
If G is any group, let H and K be normal subgroups of G such that H ![]() K = {e}. Prove the following:
K = {e}. Prove the following:
1 Let h1 and h2 be any two elements of H, and k1 and k2 any two elements of K.
h1k1 = h2k impliesh1 = h2andk1 = k2
(HINT: If h1k1 = h2k2, then ![]() h1 ∈ H
h1 ∈ H ![]() K and k2
K and k2![]() ∈ H
∈ H ![]() K. Explain why.)
K. Explain why.)
2 For any h ∈ H and k ∈ K, hk = kh. (HINT: hk = kh iff hkh−lk−l = e. Use the fact that H and K are normal.)
3 Now, make the additional assumption that G = HK that is, every x in G can be written as x = hk for some h ∈ H and k ∈ K. Then the function ϕ(h,k) = hk is an isomorphism from H × K onto G.
We have thus proved the following: If H and K are normal subgroups of G,such that H ![]() K= {e} and G = HK, then G ≅ H × K. G is sometimes called the inner direct product of H and K.
K= {e} and G = HK, then G ≅ H × K. G is sometimes called the inner direct product of H and K.
† I. Conjugate Subgroups
Let H be a subgroup of G. For any a ∈ G, let aHa−l = {axa−l :x ∈H}; aHa−l is called a conjugate of H. Prove the following:
1 For each a ∈ G, aHa−l is a subgroup of G.
2 For each a ∈ G, H ≅ aHa−1.
3 H is a normal subgroup of G iff H = aHa−1 for every a ∈ G.
In the remaining exercises of this set, let G be a finite group. By the normalizer of H we mean the set N(H) = {a ∈G: axa−1 ∈ H for every x ∈ H}.
# 4 If a∈ N(H), then aHa−1 = H. (Remember that G is now a finite group.)
5 N(H) is a subgroup of G.
6 H ⊆ N(H). Furthermore, H is a normal subgroup of N(H).
In parts 7–10, let N = N(H).
7 For any a,b ∈G, aHa−1 = bHb−1 iff b−1a∈N(H).
# 8 There is a one-to-one correspondence between the set of conjugates of H and the set of cosets of N. (Thus, there are as many conjugates of H as cosets of N.)
9 H has exactly (G :N) conjugates. In particular, the number of distinct conjugates of if H is a divisor of |G|.
10 Let K be any subgroup of G, let K* = {Na : a ∈ K}, and let
XK = {aHa−l: a ∈ K}
Argue as in part 8 to prove that XK is in one-to-one correspondence with K*. Conclude that the number of elements in XK is a divisor of |K|.