A Book of Abstract Algebra, Second Edition (1982)
Chapter 1. WHY ABSTRACT ALGEBRA?
When we open a textbook of abstract algebra for the first time and peruse the table of contents, we are struck by the unfamiliarity of almost every topic we see listed. Algebra is a subject we know well, but here it looks surprisingly different. What are these differences, and how fundamental are they?
First, there is a major difference in emphasis. In elementary algebra we learned the basic symbolism and methodology of algebra; we came to see how problems of the real world can be reduced to sets of equations and how these equations can be solved to yield numerical answers. This technique for translating complicated problems into symbols is the basis for all further work in mathematics and the exact sciences, and is one of the triumphs of the human mind. However, algebra is not only a technique, it is also a branch of learning, a discipline, like calculus or physics or chemistry. It is a coherent and unified body of knowledge which may be studied systematically, starting from first principles and building up. So the first difference between the elementary and the more advanced course in algebra is that, whereas earlier we concentrated on technique, we will now develop that branch of mathematics called algebra in a systematic way. Ideas and general principles will take precedence over problem solving. (By the way, this does not mean that modern algebra has no applications—quite the opposite is true, as we will see soon.)
Algebra at the more advanced level is often described as modern or abstract algebra. In fact, both of these descriptions are partly misleading. Some of the great discoveries in the upper reaches of present-day algebra (for example, the so-called Galois theory) were known many years before the American Civil War ; and the broad aims of algebra today were clearly stated by Leibniz in the seventeenth century. Thus, “modern” algebra is not so very modern, after all! To what extent is it abstract? Well, abstraction is all relative; one person’s abstraction is another person’s bread and butter. The abstract tendency in mathematics is a little like the situation of changing moral codes, or changing tastes in music: What shocks one generation becomes the norm in the next. This has been true throughout the history of mathematics.
For example, 1000 years ago negative numbers were considered to be an outrageous idea. After all, it was said, numbers are for counting: we may have one orange, or two oranges, or no oranges at all; but how can we have minus an orange? The logisticians, or professional calculators, of those days used negative numbers as an aid in their computations; they considered these numbers to be a useful fiction, for if you believe in them then every linear equation ax + b = 0 has a solution (namely x = −b/a, provided a ≠ 0). Even the great Diophantus once described the solution of 4x + 6 = 2 as an absurd number. The idea of a system of numeration which included negative numbers was far too abstract for many of the learned heads of the tenth century!
The history of the complex numbers (numbers which involve ![]() ) is very much the same. For hundreds of years, mathematicians refused to accept them because they couldn’t find concrete examples or applications. (They are now a basic tool of physics.)
) is very much the same. For hundreds of years, mathematicians refused to accept them because they couldn’t find concrete examples or applications. (They are now a basic tool of physics.)
Set theory was considered to be highly abstract a few years ago, and so were other commonplaces of today. Many of the abstractions of modern algebra are already being used by scientists, engineers, and computer specialists in their everyday work. They will soon be common fare, respectably “concrete,” and by then there will be new “abstractions.”
Later in this chapter we will take a closer look at the particular brand of abstraction used in algebra. We will consider how it came about and why it is useful.
Algebra has evolved considerably, especially during the past 100 years. Its growth has been closely linked with the development of other branches of mathematics, and it has been deeply influenced by philosophical ideas on the nature of mathematics and the role of logic. To help us understand the nature and spirit of modern algebra, we should take a brief look at its origins.
ORIGINS
The order in which subjects follow each other in our mathematical education tends to repeat the historical stages in the evolution of mathematics. In this scheme, elementary algebra corresponds to the great classical age of algebra, which spans about 300 years from the sixteenth through the eighteenth centuries. It was during these years that the art of solving equations became highly developed and modern symbolism was invented.
The word “algebra”—al jebr in Arabic—was first used by Mohammed of Kharizm, who taught mathematics in Baghdad during the ninth century. The word may be roughly translated as “reunion,” and describes his method for collecting the terms of an equation in order to solve it. It is an amusing fact that the word “algebra” was first used in Europe in quite another context. In Spain barbers were called algebristas, or bonesetters (they reunited broken bones), because medieval barbers did bonesetting and bloodletting as a sideline to their usual business.
The origin of the word clearly reflects the actual context of algebra at that time, for it was mainly concerned with ways of solving equations. In fact, Omar Khayyam, who is best remembered for his brilliant verses on wine, song, love, and friendship which are collected in the Rubaiyat—but who was also a great mathematician—explicitly defined algebra as the science of solving equations.
Thus, as we enter upon the threshold of the classical age of algebra, its central theme is clearly identified as that of solving equations. Methods of solving the linear equation ax + b = 0 and the quadratic ax2 + bx + c = 0 were well known even before the Greeks. But nobody had yet found a general solution for cubic equations
x3 + ax2 + bx = c
or quartic (fourth-degree) equations
x4 + ax3 + bx2 + cx = d
This great accomplishment was the triumph of sixteenth century algebra.
The setting is Italy and the time is the Renaissance—an age of high adventure and brilliant achievement, when the wide world was reawakening after the long austerity of the Middle Ages. America had just been discovered, classical knowledge had been brought to light, and prosperity had returned to the great cities of Europe. It was a heady age when nothing seemed impossible and even the old barriers of birth and rank could be overcome. Courageous individuals set out for great adventures in the far corners of the earth, while others, now confident once again of the power of the human mind, were boldly exploring the limits of knowledge in the sciences and the arts. The ideal was to be bold and many-faceted, to “know something of everything, and everything of at least one thing.” The great traders were patrons of the arts, the finest minds in science were adepts at political intrigue and high finance. The study of algebra was reborn in this lively milieu.
Those men who brought algebra to a high level of perfection at the beginning of its classical age—all typical products of the Italian Renaissanee —were as colorful and extraordinary a lot as have ever appeared in a chapter of history. Arrogant and unscrupulous, brilliant, flamboyant, swaggering, and remarkable, they lived their lives as they did their work: with style and panache, in brilliant dashes and inspired leaps of the imagination.
The spirit of scholarship was not exactly as it is today. These men, instead of publishing their discoveries, kept them as well-guarded secrets to be used against each other in problem-solving competitions. Such contests were a popular attraction: heavy bets were made on the rival parties, and their reputations (as well as a substantial purse) depended on the outcome.
One of the most remarkable of these men was Girolamo Cardan. Cardan was born in 1501 as the illegitimate son of a famous jurist of the city of Pavia. A man of passionate contrasts, he was destined to become famous as a physician, astrologer, and mathematician—and notorious as a compulsive gambler, scoundrel, and heretic. After he graduated in medicine, his efforts to build up a medical practice were so unsuccessful that he and his wife were forced to seek refuge in the poorhouse. With the help of friends he became a lecturer in mathematics, and, after he cured the child of a senator from Milan, his medical career also picked up. He was finally admitted to the college of physicians and soon became its rector. A brilliant doctor, he gave the first clinical description of typhus fever, and as his fame spread he became the personal physician of many of the high and mighty of his day.
Cardan’s early interest in mathematics was not without a practical side. As an inveterate gambler he was fascinated by what he recognized to be the laws of chance. He wrote a gamblers’ manual entitled Book on Games of Chance, which presents the first systematic computations of probabilities. He also needed mathematics as a tool in casting horoscopes, for his fame as an astrologer was great and his predictions were highly regarded and sought after. His most important achievement was the publication of a book called Ars Magna (The Great Art), in which he presented systematically all the algebraic knowledge of his time. However, as already stated, much of this knowledge was the personal secret of its practitioners, and had to be wheedled out of them by cunning and deceit. The most important accomplishment of the day, the general solution of the cubic equation which had been discovered by Tartaglia, was obtained in that fashion.
Tartaglia’s life was as turbulent as any in those days. Born with the name of Niccolo Fontana about 1500, he was present at the occupation of Brescia by the French in 1512. He and his father fled with many others into a cathedral for sanctuary, but in the heat of battle the soldiers massacred the hapless citizens even in that holy place. The father was killed, and the boy, with a split skull and a deep saber cut across his jaws and palate, was left for dead. At night his mother stole into the cathedral and managed to carry him off; miraculously he survived. The horror of what he had witnessed caused him to stammer for the rest of his life, earning him the nickname Tartaglia, “the stammerer,” which he eventually adopted.
Tartaglia received no formal schooling, for that was a privilege of rank and wealth. However, he taught himself mathematics and became one of the most gifted mathematicians of his day. He translated Euclid and Archimedes and may be said to have originated the science of ballistics, for he wrote a treatise on gunnery which was a pioneering effort on the laws of falling bodies.
In 1535 Tartaglia found a way of solving any cubic equation of the form x3 + ax2 = b (that is, without an x term). When be announced his accomplishment (without giving any details, of course), he was challenged to an algebra contest by a certain Antonio Fior, a pupil of the celebrated professor of mathematics Scipio del Ferro. Scipio had already found a method for solving any cubic equation of the form x3 + ax = b (that is, without an x2 term), and had confided his secret to his pupil Fior. It was agreed that each contestant was to draw up 30 problems and hand the list to his opponent. Whoever solved the greater number of problems would receive a sum of money deposited with a lawyer. A few days before the contest, Tartaglia found a way of extending his method so as to solve any cubic equation. In less than 2 hours he solved all his opponent’s problems, while his opponent failed to solve even one of those proposed by Tartaglia.
For some time Tartaglia kept his method for solving cubic equations to himself, but in the end he succumbed to Cardan’s accomplished powers of persuasion. Influenced by Cardan’s promise to help him become artillery adviser to the Spanish army, he revealed the details of his method to Cardan under the promise of strict secrecy. A few years later, to Tartaglia’s unbelieving amazement and indignation, Cardan published Tartaglia’s method in his book Ars Magna. Even though he gave Tartaglia full credit as the originator of the method, there can be no doubt that he broke his solemn promise. A bitter dispute arose between the mathematicians, from which Tartaglia was perhaps lucky to escape alive. He lost his position as public lecturer at Brescia, and lived out his remaining years in obscurity.
The next great step in the progress of algebra was made by another member of the same circle. It was Ludovico Ferrari who discovered the general method for solving quartic equations—equations of the form
x4 + ax3 + bx2 + cx = d
Ferrari was Cardan’s personal servant. As a boy in Cardan’s service he learned Latin, Greek, and mathematics. He won fame after defeating Tartaglia in a contest in 1548, and received an appointment as supervisor of tax assessments in Mantua. This position brought him wealth and influence, but he was not able to dominate his own violent disposition. He quarreled with the regent of Mantua, lost his position, and died at the age of 43. Tradition has it that he was poisoned by his sister.
As for Cardan, after a long career of brilliant and unscrupulous achievement, his luck finally abandoned him. Cardan’s son poisoned his unfaithful wife and was executed in 1560. Ten years later, Cardan was arrested for heresy because he published a horoscope of Christ’s life. He spent several months in jail and was released after renouncing his heresy privately, but lost his university position and the right to publish books. He was left with a small pension which had been granted to him, for some unaccountable reason, by the Pope.
As this colorful time draws to a close, algebra emerges as a major branch of mathematics. It became clear that methods can be found to solve many different types of equations. In particular, formulas had been discovered which yielded the roots of all cubic and quartic equations. Now the challenge was clearly out to take the next step, namely, to find a formula for the roots of equations of degree 5 or higher (in other words, equations with an x5 term, or an x6 term, or higher). During the next 200 years, there was hardly a mathematician of distinction who did not try to solve this problem, but none succeeded. Progress was made in new parts of algebra, and algebra was linked to geometry with the invention of analytic geometry. But the problem of solving equations of degree higher than 4 remained unsettled. It was, in the expression of Lagrange, “a challenge to the human mind.”
It was therefore a great surprise to all mathematicians when in 1824 the work of a young Norwegian prodigy named Niels Abel came to light. In his work, Abel showed that there does not exist any formula (in the conventional sense we have in mind) for the roots of an algebraic equation whose degree is 5 or greater. This sensational discovery brings to a close what is called the classical age of algebra. Throughout this age algebra was conceived essentially as the science of solving equations, and now the outer limits of this quest had apparently been reached. In the years ahead, algebra was to strike out in new directions.
THE MODERN AGE
About the time Niels Abel made his remarkable discovery, several mathematicians, working independently in different parts of Europe, began raising questions about algebra which had never been considered before. Their researches in different branches of mathematics had led them to investigate “algebras” of a very unconventional kind—and in connection with these algebras they had to find answers to questions which had nothing to do with solving equations. Their work had important applications, and was soon to compel mathematicians to greatly enlarge their conception of what algebra is about.
The new varieties of algebra arose as a perfectly natural development in connection with the application of mathematics to practical problems. This is certainly true for the example we are about to look at first.
The Algebra of Matrices
A matrix is a rectangular array of numbers such as
![]()
Such arrays come up naturally in many situations, for example, in the solution of simultaneous linear equations. The above matrix, for instance, is the matrix of coefficients of the pair of equations
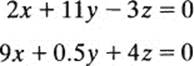
Since the solution of this pair of equations depends only on the coefficients, we may solve it by working on the matrix of coefficients alone and ignoring everything else.
We may consider the entries of a matrix to be arranged in rows and columns; the above matrix has two rows which are
(2 11 −3) and (9 0.5 4)
and three columns which are
![]()
It is a 2 × 3 matrix.
To simplify our discussion, we will consider only 2 × 2 matrices in the remainder of this section.
Matrices are added by adding corresponding entries:
![]()
The matrix
![]()
is called the zero matrix and behaves, under addition, like the number zero.
The multiplication of matrices is a little more difficult. First, let us recall that the dot product of two vectors (a, b) and (a′,b′) is
(a,b) · (a′, b′) = aa′ + bb′
that is, we multiply corresponding components and add. Now, suppose we want to multiply two matrices A and B; we obtain the product AB as follows:
The entry in the first row and first column of AB, that is, in this position
![]()
is equal to the dot product of the first row of A by the first column of B. The entry in the first row and second column of AB, in other words, this position
![]()
is equal to the dot product of the first row of A by the second column of B. And so on. For example,
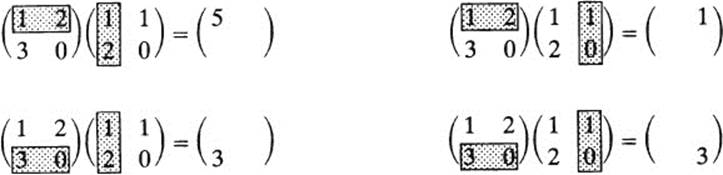
So finally,
![]()
The rules of algebra for matrices are very different from the rules of “conventional” algebra. For instance, the commutative law of multplica-tion, AB = BA, is not true. Here is a simple example:
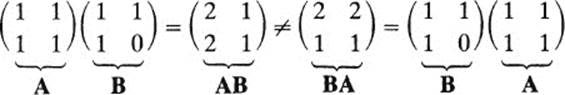
If A is a real number and A2 = 0, then necessarily A = 0; but this is not true of matrices. For example,
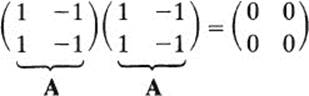
that is, A2 = 0 although A ≠ 0.
In the algebra of numbers, if AB = AC where A ≠ 0, we may cancel A and conclude that B = C. In matrix algebra we cannot. For example,
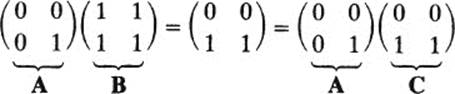
that is, AB = AC, A ≠ 0, yet B ≠ C.
The identity matrix
![]()
corresponds in matrix multiplication to the number 1; for we have AI = IA = A for every 2 × 2 matrix A. If A is a number and A2 = 1, we conclude that A = ±1 Matrices do not obey this rule. For example,
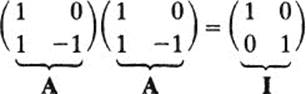
that is, A2 = I, and yet A is neither I nor −I.
No more will be said about the algebra of matrices at this point, except that we must be aware, once again, that it is a new game whose rules are quite different from those we apply in conventional algebra.
Boolean Algebra
An even more bizarre kind of algebra was developed in the mid-nineteenth century by an Englishman named George Boole. This algebra—subsequently named boolean algebra after its inventor—has a myriad of applications today. It is formally the same as the algebra of sets.
If S is a set, we may consider union and intersection to be operations on the subsets of 5. Let us agree provisionally to write
A + B for A ∪ B
and
A · B for A ∩ B
(This convention is not unusual.) Then,
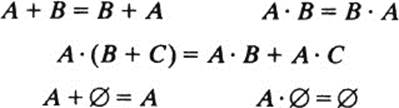
and so on.
These identities are analogous to the ones we use in elementary algebra. But the following identities are also true, and they have no counterpart in conventional algebra:
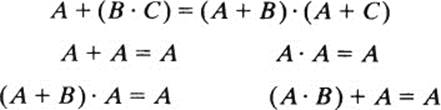
and so on.
This unusual algebra has become a familiar tool for people who work with electrical networks, computer systems, codes, and so on. It is as different from the algebra of numbers as it is from the algebra of matrices.
Other exotic algebras arose in a variety of contexts, often in connection with scientific problems. There were “complex” and “hypercomplex” algebras, algebras of vectors and tensors, and many others. Today it is estimated that over 200 different kinds of algebraic systems have been studied, each of which arose in connection with some application or specific need.
Algebraic Structures
As legions of new algebras began to occupy the attention of mathematicians, the awareness grew that algebra can no longer be conceived merely as the science of solving equations. It had to be viewed much more broadly as a branch of mathematics capable of revealing general principles which apply equally to all known and all possible algebras.
What is it that all algebras have in common? What trait do they share which lets us refer to all of them as “algebras”? In the most general sense, every algebra consists of a set (a set of numbers, a set of matrices, a set of switching components, or any other kind of set) and certain operations on that set. An operation is simply a way of combining any two members of a set to produce a unique third member of the same set.
Thus, we are led to the modern notion of algebraic structure. An algebraic structure is understood to be an arbitrary set, with one or more operations defined on it. And algebra, then, is defined to be the study of algebraic structures.
It is important that we be awakened to the full generality of the notion of algebraic structure. We must make an effort to discard all our preconceived notions of what an algebra is, and look at this new notion of algebraic structure in its naked simplicity. Any set, with a rule (or rules) for combining its elements, is already an algebraic structure. There does not need to be any connection with known mathematics. For example, consider the set of all colors (pure colors as well as color combinations), and the operation of mixing any two colors to produce a new color. This may be conceived as an algebraic structure. It obeys certain rules, such as the commutative law (mixing red and blue is the same as mixing blue and red). In a similar vein, consider the set of all musical sounds with the operation of combining any two sounds to produce a new (harmonious or disharmonious) combination.
As another example, imagine that the guests at a family reunion have made up a rule for picking the closest common relative of any two persons present at the reunion (and suppose that, for any two people at the reunion, their closest common relative is also present at the reunion). This too, is an algebraic structure: we have a set (namely the set of persons at the reunion) and an operation on that set (namely the “closest common relative” operation).
As the general notion of algebraic structure became more familiar (it was not fully accepted until the early part of the twentieth century), it was bound to have a profound influence on what mathematicians perceived algebra to be. In the end it became clear that the purpose of algebra is to study algebraic structures, and nothing less than that. Ideally it should aim to be a general science of algebraic structures whose results should have applications to particular cases, thereby making contact with the older parts of algebra. Before we take a closer look at this program, we must briefly examine another aspect of modern mathematics, namely, the increasing use of the axiomatic method.
AXIOMS
The axiomatic method is beyond doubt the most remarkable invention of antiquity, and in a sense the most puzzling. It appeared suddenly in Greek geometry in a highly developed form—already sophisticated, elegant, and thoroughly modern in style. Nothing seems to have foreshadowed it and it was unknown to ancient mathematicians before the Greeks. It appears for the first time in the light of history in the great textbook of early geometry, Euclid’s Elements. Its origins—the first tentative experiments in formal deductive reasoning which must have preceded it—remain steeped in mystery.
Euclid’s Elements embodies the axiomatic method in its purest form. This amazing book contains 465 geometric propositions, some fairly simple, some of astounding complexity. What is really remarkable, though, is that the 465 propositions, forming the largest body of scientific knowledge in the ancient world, are derived logically from only 10 premises which would pass as trivial observations of common sense. Typical of the premises are the following:
Things equal to the same thing are equal to each other.
The whole is greater than the part.
A straight line can be drawn through any two points.
All right angles are equal.
So great was the impression made by Euclid’s Elements on following generations that it became the model of correct mathematical form and remains so to this day.
It would be wrong to believe there was no notion of demonstrative mathematics before the time of Euclid. There is evidence that the earliest geometers of the ancient Middle East used reasoning to discover geometric principles. They found proofs and must have hit upon many of the same proofs we find in Euclid. The difference is that Egyptian and Babylonian mathematicians considered logical demonstration to be an auxiliary process, like the preliminary sketch made by artists—a private mental process which guided them to a result but did not deserve to be recorded. Such an attitude shows little understanding of the true nature of geometry and does not contain the seeds of the axiomatic method.
It is also known today that many—maybe most—of the geometric theorems in Euclid’s Elements came from more ancient times, and were probably borrowed by Euclid from Egyptian and Babylonian sources. However, this does not detract from the greatness of his work. Important as are the contents of the Elements, what has proved far more important for posterity is the formal manner in which Euclid presented these contents. The heart of the matter was the way he organized geometric facts—arranged them into a logical sequence where each theorem builds on preceding theorems and then forms the logical basis for other theorems.
(We must carefully note that the axiomatic method is not a way of discovering facts but of organizing them. New facts in mathematics are found, as often as not, by inspired guesses or experienced intuition. To be accepted, however, they should be supported by proof in an axiomatic system.)
Euclid’s Elements has stood throughout the ages as the model of organized, rational thought carried to its ultimate perfection. Mathematicians and philosophers in every generation have tried to imitate its lucid perfection and flawless simplicity. Descartes and Leibniz dreamed of organizing all human knowledge into an axiomatic system, and Spinoza created a deductive system of ethics patterned after Euclid’s geometry. While many of these dreams have proved to be impractical, the method popularized by Euclid has become the prototype of modern mathematical form. Since the middle of the nineteenth century, the axiomatic method has been accepted as the only correct way of organizing mathematical knowledge.
To perceive why the axiomatic method is truly central to mathematics, we must keep one thing in mind: mathematics by its nature is essentially abstract. For example, in geometry straight lines are not stretched threads, but a concept obtained by disregarding all the properties of stretched threads except that of extending in one direction. Similarly, the concept of a geometric figure is the result of idealizing from all the properties of actual objects and retaining only their spatial relationships. Now, since the objects of mathematics are abstractions, it stands to reason that we must acquire knowledge about them by logic and not by observation or experiment (for how can one experiment with an abstract thought?).
This remark applies very aptly to modern algebra. The notion of algebraic structure is obtained by idealizing from all particular, concrete systems of algebra. We choose to ignore the properties of the actual objects in a system of algebra (they may be numbers, or matrices, or whatever—we disregard what they are), and we turn our attention simply to the way they combine under the given operations. In fact, just as we disregard what the objects in a system are, we also disregard what the operations do to them. We retain only the equations and inequalities which hold in the system, for only these are relevant to algebra. Everything else may be discarded. Finally, equations and inequalities may be deduced from one another logically, just as spatial relationships are deduced from each other in geometry.
THE AXIOMATICS OF ALGEBRA
Let us remember that in the mid-nineteenth century, when eccentric new algebras seemed to show up at every turn in mathematical research, it was finally understood that sacrosanct laws such as the identities ab = ba and a(bc) = (ab)c are not inviolable—for there are algebras in which they do not hold. By varying or deleting some of these identities, or by replacing them by new ones, an enormous variety of new systems can be created.
Most importantly, mathematicians slowly discovered that all the algebraic laws which hold in any system can be derived from a few simple, basic ones. This is a genuinely remarkable fact, for it parallels the discovery made by Euclid that a few very simple geometric postulates are sufficient to prove all the theorems of geometry. As it turns out, then, we have the same phenomenon in algebra: a few simple algebraic equations offer themselves naturally as axioms, and from them all other facts may be proved.
These basic algebraic laws are familiar to most high school students today. We list them here for reference. We assume that A is any set and there is an operation on A which we designate with the symbol *
a * b = b * a(1)
If Equation (1) is true for any two elements a and b in A, we say that the operation * is commutative. What it means, of course, is that the value of a * b (or b * a) is independent of the order in which a and b are taken.
a * (b * c) = (a * b) *c(2)
If Equation (2) is true for any three elements a, b, and c in A, we say the operation * is associative. Remember that an operation is a rule for combining any two elements, so if we want to combine three elements, we can do so in different ways. If we want to combine a, b, and c without changing their order, we may either combine a with the result of combining b and c, which produces a *(b * c); or we may first combine a with b, and then combine the result with c, producing (a * b)* c. The associative law asserts that these two possible ways of combining three elements (without changing their order) yield the same result.
There exists an element e in A such that
e * a = a and a * e = a for every a in A(3)
If such an element e exists in A, we call it an identity element for the operation *. An identity element is sometimes called a “neutral” element, for it may be combined with any element a without altering a. For example, 0 is an identity element for addition, and 1 is an identity element for multiplication.
For every element a in A, there is an element a−l (“a inverse”) in A such that
a * a−l = e and a−1 * a = e(4)
If statement (4) is true in a system of algebra, we say that every element has an inverse with respect to the operation *. The meaning of the inverse should be clear: the combination of any element with its inverse produces the neutral element (one might roughly say that the inverse of a “neutralizes” a). For example, if A is a set of numbers and the operation is addition, then the inverse of any number a is (−a); if the operation is multiplication, the inverse of any a≠ 0 is 1/a.
Let us assume now that the same set A has a second operation, symbolized by ⊥, as well as the operation * :
a * (b ⊥ c) = (a * b) ⊥ (a * c)(5)
If Equation (5) holds for any three elements a, b, and c in A, we say that * is distributive over ⊥. If there are two operations in a system, they must interact in some way; otherwise there would be no need to consider them together. The distributive law is the most common way (but not the only possible one) for two operations to be related to one another.
There are other “basic” laws besides the five we have just seen, but these are the most common ones. The most important algebraic systems have axioms chosen from among them. For example, when a mathematician nowadays speaks of a ring, the mathematician is referring to a set A with two operations, usually symbolized by + and ·, having the following axioms:
Addition is commutative and associative, it has a neutral element commonly symbolized by 0, and every element a has an inverse –a with respect to addition. Multiplication is associative, has a neutral element 1, and is distributive over addition.
Matrix algebra is a particular example of a ring, and all the laws of matrix algebra may be proved from the preceding axioms. However, there are many other examples of rings: rings of numbers, rings of functions, rings of code “words,” rings of switching components, and a great many more. Every algebraic law which can be proved in a ring (from the preceding axioms) is true in every example of a ring. In other words, instead of proving the same formula repeatedly—once for numbers, once for matrices, once for switching components, and so on—it is sufficient nowadays to prove only that the formula holds in rings, and then of necessity it will be true in all the hundreds of different concrete examples of rings.
By varying the possible choices of axioms, we can keep creating new axiomatic systems of algebra endlessly. We may well ask: is it legitimate to study any axiomatic system, with any choice of axioms, regardless of usefulness, relevance, or applicability? There are “radicals” in mathematics who claim the freedom for mathematicians to study any system they wish, without the need to justify it. However, the practice in established mathematics is more conservative: particular axiomatic systems are investigated on account of their relevance to new and traditional problems and other parts of mathematics, or because they correspond to particular applications.
In practice, how is a particular choice of algebraic axioms made? Very simply: when mathematicians look at different parts of algebra and notice that a common pattern of proofs keeps recurring, and essentially the same assumptions need to be made each time, they find it natural to single out this choice of assumptions as the axioms for a new system. All the important new systems of algebra were created in this fashion.
ABSTRACTION REVISITED
Another important aspect of axiomatic mathematics is this: when we capture mathematical facts in an axiomatic system, we never try to reproduce the facts in full, but only that side of them which is important or relevant in a particular context. This process of selecting what is relevant and disregarding everything else is the very essence of abstraction.
This kind of abstraction is so natural to us as human beings that we practice it all the time without being aware of doing so. Like the Bourgeois Gentleman in Molière’s play who was amazed to learn that he spoke in prose, some of us may be surprised to discover how much we think in abstractions. Nature presents us with a myriad of interwoven facts and sensations, and we are challenged at every instant to single out those which are immediately relevant and discard the rest. In order to make our surroundings comprehensible, we must continually pick out certain data and separate them from everything else.
For natural scientists, this process is the very core and essence of what they do. Nature is not made up of forces, velocities, and moments of inertia. Nature is a whole—nature simply is! The physicist isolates certain aspects of nature from the rest and finds the laws which govern these abstractions.
It is the same with mathematics. For example, the system of the integers (whole numbers), as known by our intuition, is a complex reality with many facets. The mathematician separates these facets from one another and studies them individually. From one point of view the set of the integers, with addition and multiplication, forms a ring (that is, it satisfies the axioms stated previously). From another point of view it is an ordered set, and satisfies special axioms of ordering. On a different level, the positive integers form the basis of “recursion theory,” which singles out the particular way positive integers may be constructed, beginning with 1 and adding 1 each time.
It therefore happens that the traditional subdivision of mathematics into subject matters has been radically altered. No longer are the integers one subject, complex numbers another, matrices another, and so on; instead, particular aspects of these systems are isolated, put in axiomatic form, and studied abstractly without reference to any specific objects. The other side of the coin is that each aspect is shared by many of the traditional systems: for example, algebraically the integers form a ring, and so do the complex numbers, matrices, and many other kinds of objects.
There is nothing intrinsically new about this process of divorcing properties from the actual objects having the properties; as we have seen, it is precisely what geometry has done for more than 2000 years. Somehow, it took longer for this process to take hold in algebra.
The movement toward axiomatics and abstraction in modern algebra began about the 1830s and was completed 100 years later. The movement was tentative at first, not quite conscious of its aims, but it gained momentum as it converged with similar trends in other parts of mathematics. The thinking of many great mathematicians played a decisive role, but none left a deeper or longer lasting impression than a very young Frenchman by the name of Évariste Galois.
The story of Évariste Galois is probably the most fantastic and tragic in the history of mathematics. A sensitive and prodigiously gifted young man, he was killed in a duel at the age of 20, ending a life which in its brief span had offered him nothing but tragedy and frustration. When he was only a youth his father commited suicide, and Galois was left to fend for himself in the labyrinthine world of French university life and student politics. He was twice refused admittance to the Ecole Polytechnique, the most prestigious scientific establishment of its day, probably because his answers to the entrance examination were too original and unorthodox. When he presented an early version of his important discoveries in algebra to the great academician Cauchy, this gentleman did not read the young student’s paper, but lost it. Later, Galois gave his results to Fourier in the hope of winning the mathematics prize of the Academy of Sciences. But Fourier died, and that paper, too, was lost. Another paper submitted to Poisson was eventually returned because Poisson did not have the interest to read it through.
Galois finally gained admittance to the École Normale, another focal point of research in mathematics, but he was soon expelled for writing an essay which attacked the king. He was jailed twice for political agitation in the student world of Paris. In the midst of such a turbulent life, it is hard to believe that Galois found time to create his colossally original theories on algebra.
What Galois did was to tie in the problem of finding the roots of equations with new discoveries on groups of permutations. He explained exactly which equations of degree 5 or higher have solutions of the traditional kind—and which others do not. Along the way, he introduced some amazingly original and powerful concepts, which form the framework of much algebraic thinking to this day. Although Galois did not work explicitly in axiomatic algebra (which was unknown in his day), the abstract notion of algebraic structure is clearly prefigured in his work.
In 1832, when Galois was only 20 years old, he was challenged to a duel. What argument led to the challenge is not clear: some say the issue was political, while others maintain the duel was fought over a fickle lady’s wavering love. The truth may never be known, but the turbulent, brilliant, and idealistic Galois died of his wounds. Fortunately for mathematics, the night before the duel he wrote down his main mathematical results and entrusted them to a friend. This time, they weren’t lost—but they were only published 15 years after his death. The mathematical world was not ready for them before then!
Algebra today is organized axiomatically, and as such it is abstract. Mathematicians study algebraic structures from a general point of view, compare different structures, and find relationships between them. This abstraction and generalization might appear to be hopelessly impractical—but it is not! The general approach in algebra has produced powerful new methods for “algebraizing” different parts of mathematics and science, formulating problems which could never have been formulated before, and finding entirely new kinds of solutions.
Such excursions into pure mathematical fancy have an odd way of running ahead of physical science, providing a theoretical framework to account for facts even before those facts are fully known. This pattern is so characteristic that many mathematicians see themselves as pioneers in a world of possibilities rather than facts. Mathematicians study structure independently of content, and their science is a voyage of exploration through all the kinds of structure and order which the human mind is capable of discerning.