A Book of Abstract Algebra, Second Edition (1982)
Chapter 24. RINGS OF POLYNOMIALS
In elementary algebra an important role is played by polynomials in an unknown x. These are expressions such as
![]()
whose terms are grouped in powers of x. The exponents, of course, are positive integers and the coefficients are real or complex numbers.
Polynomials are involved in countless applications—applications of every kind and description. For example, polynomial functions are the easiest functions to compute, and therefore one commonly attempts to approximate arbitrary functions by polynomial functions. A great deal of effort has been expended by mathematicians to find ways of achieving this.
Aside from their uses in science and computation, polynomials come up very naturally in the general study of rings, as the following example will show:
Suppose we wish to enlarge the ring ![]() by adding to it the number π. It is easy to see that we will have to adjoin to
by adding to it the number π. It is easy to see that we will have to adjoin to ![]() other new numbers besides just π; for the enlarged ring (containing π as well as all the integers) will also contain such things as − π, π + 7, 6π2 − 11, and so on.
other new numbers besides just π; for the enlarged ring (containing π as well as all the integers) will also contain such things as − π, π + 7, 6π2 − 11, and so on.
As a matter of fact, any ring which contains ![]() as a subring and which also contains the number π will have to contain every number of the form
as a subring and which also contains the number π will have to contain every number of the form
aπn + bπn”1 + ⋯ + kπ + l
where a, b, …, k, l are integers. In other words, it will contain all the polynomial expressions in π with integer coefficients.
But the set of all the polynomial expressions in π with integer coefficients is a ring. (It is a subring of ![]() because it is obvious that the sum and product of any two polynomials in π is again a polynomial in π.) This ring contains
because it is obvious that the sum and product of any two polynomials in π is again a polynomial in π.) This ring contains ![]() because every integer a is a polynomial with a constant term only, and it also contains π.
because every integer a is a polynomial with a constant term only, and it also contains π.
Thus, if we wish to enlarge the ring ![]() by adjoining to it the new number π, it turns out that the “next largest” ring after
by adjoining to it the new number π, it turns out that the “next largest” ring after ![]() which contains
which contains ![]() as a subring and includes π, is exactly the ring of all the polynomials in π with coefficients in
as a subring and includes π, is exactly the ring of all the polynomials in π with coefficients in ![]() .
.
As this example shows, aside from their practical applications, polynomials play an important role in the scheme of ring theory because they are precisely what we need when we wish to enlarge a ring by adding new elements to it.
In elementary algebra one considers polynomials whose coefficients are real numbers, or in some cases, complex numbers. As a matter of fact, the properties of polynomials are pretty much independent of the exact nature of their coefficients. All we need to know is that the coefficients are contained in some ring. For convenience, we will assume this ring is a commutative ring with unity.
Let A be a commutative ring with unity. Up to now we have used letters to denote elements or sets, but now we will use the letter x in a different way. In a polynomial expression such as ax2 + bx + c, where a, b, c ∈ A, we do not consider x to be an element of A, but rather x is a symbol which we use in an entirely formal way. Later we will allow the substitution of other things for x, but at present x is simply a placeholder.
Notationally, the terms of a polynomial may be listed in either ascending or descending order. For example, 4x3 – 3x2 + x + 1 and 1 + x – 3x2 + 4x3 denote the same polynomial. In elementary algebra descending order is preferred, but for our purposes ascending order is more convenient.
Let A be a commutative ring with unity, and x an arbitrary symbol. Every expression of the form
a0 + a1x + a2x2 + ⋯ + anxn
is called a polynomial in x with coefficients in A, or more simply, a polynomial in x over A. The expressions akxk, for k ∈ {1, …, n},are called the terms of the polynomial.
Polynomials in x are designated by symbols such as a(x), b(x), q(x), and so on. If a(x) = a0 + a1x + ⋯ + anxn is any polynomial and akxk is any one of its terms, ak is called the coefficient of xk. By the degree of a polynomial a(x) we mean the greatest n such that the coefficient of xn is not zero. In other words, if a(x) has degree n, this means that an ≠ 0 but am = 0 for every m > n. The degree of a(x) is symbolized by
deg a(x)
For example, 1 + 2x − 3x2 + x3 is a polynomial degree 3.
The polynomial 0 + 0x + 0x2 + ⋯ all of whose coefficients are equal to zero is called the zero polynomial, and is symbolized by 0. It is the only polynomial whose degree is not defined (because it has no nonzero coefficient).
If a nonzero polynomial a(x) = a0 + a1x + ⋯ + anxn has degree n, then an is called its leading coefficient: it is the last nonzero coefficient of a(x). The term anxn is then called its leading term, while a0 is called its constant term.
If a polynomial a(x) has degree zero, this means that its constant term a0 is its only nonzero term: a(x) is a constant polynomial. Beware of confusing a polynomial of degree zero with the zero polynomial.
Two polynomials a(x) and b(x) are equal if they have the same degree and corresponding coefficients are equal. Thus, if a(x) = a0 + ⋯ + anxn is of degree n, and b(x) = b0 + ⋯ + bmxm is of degree m, then a(x) = b(x) iff n = m and ak = bk for each k from 0 to n.
The familiar sigma notation for sums is useful for polynomials. Thus,
![]()
with the understanding that x0 = 1.
Addition and multiplication of polynomials is familiar from elementary algebra. We will now define these operations formally. Throughout these definitions we let a(x) and b(x) stand for the following polynomials:
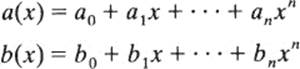
Here we do not assume that a(x) and b(x) have the same degree, but allow ourselves to insert zero coefficients if necessary to achieve uniformity of appearance.
We add polynomials by adding corresponding coefficients. Thus,
a(x) + b(x) = (a0 + b0) + (a1, + b1)x + ⋯ + (an + bn)xn
Note that the degree of a(x) + b(x) is less than or equal to the higher of the two degrees, deg a(x) and deg b(x).
Multiplication is more difficult, but quite familiar:
a(x)b(x)
= a0b0 + (a0b1 + b0a1)x + (a0b2 + a1 b1 + a2 b0)x2 + ⋯ + an bn x2n
In other words, the product of a(x) and b(x) is the polynomial
c(x) = c0 + c1x + ⋯ + c2n x2n
whose kth coefficient (for any k from 0 to 2n) is
![]()
This is the sum of all the aibj for which i + j = k. Note that deg [a(x)b(x)] ≤ deg a(x) + deg b(x).
If A is any ring, the symbol
A[x]
designates the set of all the polynomials in x whose coefficients are in A, with addition and multiplication of polynomials as we have just defined them.
Theorem 1 Let A be a commutative ring with unity. Then A[x] is a commutative ring with unity.
PROOF: To prove this theorem, we must show systematically that A[x] satisfies all the axioms of a commutative ring with unity. Throughout the proof, let a(x), b(x), and c(x) stand for the following polynomials:
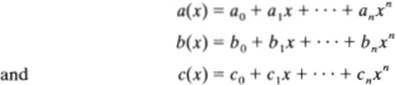
The axioms which involve only addition are easy to check: for example, addition is commutative because
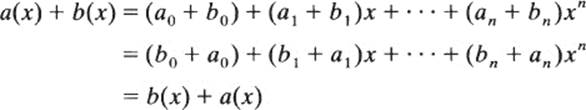
The associative law of addition is proved similarly, and is left as an exercise. The zero polynomial has already been described, and the negative of a(x) is
– a(x) = (– a0) + (– a1)x + ⋯ + (– an)xn
To prove that multiplication is associative requires some care. Let b(x)c(x) = d(x), where d(x) = d0 + d1x + ⋯ + d2nx2n. By the definition of polynomial multiplication, the kth coefficient of b(x)c(x) is
![]()
Then a(x)[b(x)c(x)] = a(x)d(x) = e(x), where e(x) = e0 + e1x + ⋯ + e3nx3n. Now, the lth coefficient of a(x)d(x) is
![]()
It is easy to see that the sum on the right consists of all the terms ah bi cj such that h + i + j = l Thus,
![]()
For each l from 0 to 3n, el is the lth coefficient of a(x)[b(x)c(x)].
If we repeat this process to find the lth coefficient of [a(x) b(x)]c(x), we discover that it, too, is el Thus,
a(x)[b(x)c(x)] = [a(x)b(x)]c(x)
To prove the distributive law, let a(x)[b(x) + c(x)] = d{x) where d(x) = d0 + d1x + ⋯ + d2nx2n. By the definitions of polynomial addition and multiplication, the kth coefficient a(x)[b(x) + c(x)] is
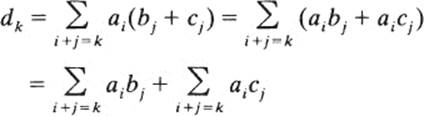
But Σi+j = k aibj. is exactly the kth coefficient of a(x) b(x), and Σi + j = k aicj is the kth coefficient of a(x)c(x), hence dk is equal to the kth coefficient of a(x) b(x) + a(x)c(x). This proves that
a(x)[b(x) + c(x)] = a(x)b(x) + a(x)c(x)
The commutative law of multiplication is simple to verify and is left to the student. Finally, the unity polynomial is the constant polynomial 1. ■
Theorem 2 If A is an integral domain, then A[x] is an integral domain.
PROOF: If a(x) and b(x) are nonzero polynomials, we must show that their product a(x) b(x) is not zero. Let an be the leading coefficient of a(x), and bm the leading coefficient of b(x). By definition, an ≠ 0, and bm ≠ 0. Thus anbm≠ 0 because A is an integral domain. It follows that a(x) b(x) has a nonzero coefficient (namely, an bm), so it is not the zero polynomial. ■
If A is an integral domain, we refer to A[x] as a domain of polynomials, because A[x] is an integral domain. Note that by the preceding proof, if an and bm are the leading coefficients of a(x) and b(x), then anbm is the leading coefficient of a(x) b(x). Thus, deg a(x)b(x) = n + m: In a domain of polynomials A[x], where A is an integral domain,
deg[a(x) · b(x)] = deg a(x) + deg b(x)
In the remainder of this chapter we will look at a property of polynomials which is of special interest when all the coefficients lie in a field. Thus, from this point forward, let F be a field, and let us consider polynomials belonging to F[x].
It would be tempting to believe that if F is a field then F[x] also is a field. However, this is not so, for one can easily see that the multiplicative inverse of a polynomial is not generally a polynomial. Nevertheless, by Theorem 2, F[x] is an integral domain.
Domains of polynomials over a field do, however, have a very special property: any polynomial a(x) may be divided by any nonzero polynomial b(x) to yield a quotient q(x) and a remainder r(x). The remainder is either 0, or if not, its degree is less than the degree of the divisor b(x). For example, x2 may be divided by x – 2 to give a quotient of x + 2 and a remainder of 4:
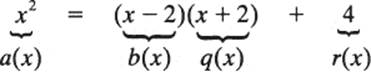
This kind of polynomial division is familiar to every student of elementary algebra. It is customarily set up as follows:
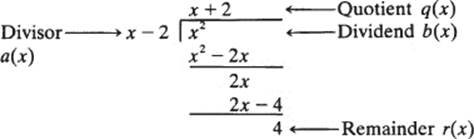
The process of polynomial division is formalized in the next theorem.
Theorem 3: Division algorithm for polynomials If a(x) and b(x) are polynomials over a field F, and b(x) ≠ 0, there exist polynomials q(x) and r(x) over F such that
a(x) = b(x)q(x) + r(x)
and
r(x) = 0 or deg r(x) < deg b(x)
PROOF: Let b(x) remain fixed, and let us show that every polynomial a(x) satisfies the following condition:
There exist polynomials q(x) and r(x) over F such that a(x) = b(x) q(x) + r(x), and r(x) = 0 or deg r(x) < deg b(x).
We will assume there are polynomials a(x) which do not fulfill the condition, and from this assumption we will derive a contradiction. Let a(x) be a polynomial of lowest degree which fails to satisfy the conditions. Note that a(x) cannot be zero, because we can express 0 as 0 = b(x) · 0 + 0, whereby a(x) would satisfy the conditions. Furthermore, deg a(x) ≥ deg b(x), for if deg a(x) < deg b(x) then we could write a(x) = b(x) · 0 + a(x), so again a(x) would satisfy the given conditions.
Let a(x) = a0 + ⋯ + anxn and b(x) = b0 + ⋯ + bmxm. Define a new polynomial
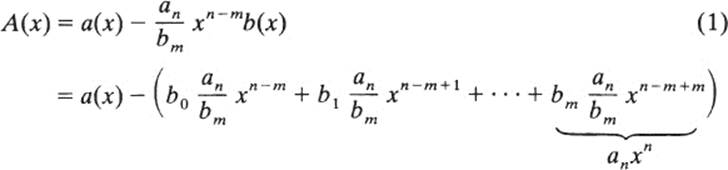
This expression is the difference of two polynomials both of degree n and both having the same leading term anxn. Because anxn cancels in the subtraction, A(x) has degree less than n.
Remember that a(x) is a polynomial of least degree which fails to satisfy the given condition; hence A(x) does satisfy it. This means there are polynomials p(x) and r(x) such that
A(x) = b(x)p(x) + r(x)
where r(x) = 0 or deg r(x) < deg b(x). But then
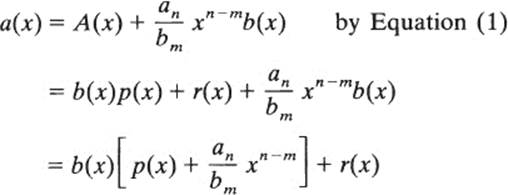
If we let p(x) + (an/bm)xn – m be renamed q(x), then a(x) = b(x)q(x) + r(x), so a(x) fulfills the given condition. This is a contradiction, as required. ■
EXERCISES
A. Elementary Computation in Domains of Polynomials
REMARK ON NOTATION: In some of the problems which follow, we consider polynomials with coefficients in ![]() n for various n. To simplify notation, we denote the elements of
n for various n. To simplify notation, we denote the elements of ![]() n by 1, 2, …, n – 1 rather than the more correct
n by 1, 2, …, n – 1 rather than the more correct ![]() .
.
# 1 Let a(x) = 2x2 + 3x + 1 and b(x) = x3 + 5x2 + x. Compute a(x) + b(x), a(x) – b(x) and a(x)b(x) in ![]() [x],
[x], ![]() 5[x],
5[x], ![]() 6[x], and
6[x], and ![]() 7[x].
7[x].
2 Find the quotient and remainder when x3 + x2 + x + 1 is divided by x2 + 3x + 2 in ![]() [x] and in
[x] and in ![]() 5[x].
5[x].
3 Find the quotient and remainder when x3 + 2 is divided by 2x2 + 3x + 4 in ![]() [x], in
[x], in ![]() 3[x], and in
3[x], and in ![]() 5[x].
5[x].
We call b(x) a factor of a(x) if a(x) = b(x)q(x) for some q(x), that is, if the remainder when a(x) is divided by b(x) is equal to zero.
4 Show that the following is true in A[x] for any ring A: For any odd n,
(a) x + 1 is a factor of xn + 1.
(b) x + 1 is a factor of xn + xn–1 + ⋯ + x + 1.
5 Prove the following: In ![]() 3[x], x + 2 is a factor of xm + 2, for all m. In
3[x], x + 2 is a factor of xm + 2, for all m. In ![]() n[x], x + (x – 1) is a factor of xm + (n − 1), for all m and n.
n[x], x + (x – 1) is a factor of xm + (n − 1), for all m and n.
6 Prove that there is no integer m such that 3x2 + 4x + m is a factor of 6x4 + 50 in ![]() [x].
[x].
7 For what values of n is x2 + 1 a factor of x5 + 5x + 6 in ![]() n[x]?
n[x]?
B. Problems Involving Concepts and Definitions
1 Is x8 + 1 = x3 + 1 in ![]() 5[x]? Explain your answer.
5[x]? Explain your answer.
2 Is there any ring A such that in A[x], some polynomial of degree 2 is equal to a polynomial of degree 4? Explain.
# 3 Write all the quadratic polynomials in ![]() 5[x]. How many are there? How many cubic polynomials are there in
5[x]. How many are there? How many cubic polynomials are there in ![]() 5[x]? More generally, how many polynomials of degree m are there in
5[x]? More generally, how many polynomials of degree m are there in ![]() n[x]?
n[x]?
4 Let A be an integral domain; prove the following:
If (x + 1)2 = x2 + 1 in A[x], then A must have characteristic 2.
If (x + 1)4 = x4 + 1 in A[x], then A must have characteristic 2.
If (x + 1)6 = x6 + 2x3 + 1 in A[x], then A must have characteristic 3.
5 Find an example of each of the following in ![]() 8[x]: a divisor of zero, an invertible element. (Find nonconstant examples.)
8[x]: a divisor of zero, an invertible element. (Find nonconstant examples.)
6 Explain why x cannot be invertible in any A[x], hence no domain of polynomials can ever be a field.
7 There are rings such as P3 in which every element ≠0,1 is a divisor of zero. Explain why this cannot happen in any ring of polynomials A[x], even when A is not an integral domain.
8 Show that in every A[x], there are elements ≠0,1 which are not idempotent, and elements ≠0,1 which are not nilpotent.
C. Rings A[x] Where A Is Not an Integral Domain
1 Prove: If A is not an integral domain, neither is A[x].
2 Give examples of divisors of zero, of degrees 0, 1, and 2, in ![]() 4[x].
4[x].
3 In ![]() 10[x], (2x + 2)(2x + 2) = (2x + 2)(5x3 + 2x + 2), yet (2x + 2) cannot be canceled in this equation. Explain why this is possible in
10[x], (2x + 2)(2x + 2) = (2x + 2)(5x3 + 2x + 2), yet (2x + 2) cannot be canceled in this equation. Explain why this is possible in ![]() 10[x], but not in
10[x], but not in ![]() 5[x].
5[x].
4 Give examples in ![]() 4[x], in
4[x], in ![]() 6[x], and in Z9[x] of polynomials a(x) and b(x) such that deg a(x)b(x) < deg a(x) + deg b(x).
6[x], and in Z9[x] of polynomials a(x) and b(x) such that deg a(x)b(x) < deg a(x) + deg b(x).
5 If A is an integral domain, we have seen that in A[x],
deg a(x)b(x) = deg a(x) + deg b(x)
Show that if A is not an integral domain, we can always find polynomials a(x) and b(x) such that deg a(x)b(x) < deg a(x) + deg b(x).
6 Show that if A is an integral domain, the only invertible elements in A[x] are the constant polynomials with inverses in A. Then show that in ![]() 4[x] there are invertible polynomials of all degrees.
4[x] there are invertible polynomials of all degrees.
# 7 Give all the ways of factoring x2 into polynomials of degree 1 in ![]() 9[x]; in
9[x]; in ![]() 5[x]. Explain the difference in behavior.
5[x]. Explain the difference in behavior.
8 Find all the square roots of x2 + x + 4 in ![]() 5[x]. Show that in
5[x]. Show that in ![]() 8[x], there are infinitely many square roots of 1.
8[x], there are infinitely many square roots of 1.
D. Domains A[x] Where A Has Finite Characteristic
In each of the following, let A be an integral domain:
1 Prove that if A has characteristic p, then A[x] has characteristic p.
2 Use part 1 to give an example of an infinite integral domain with finite characteristic.
3 Prove: If A has characteristic 3, then x + 2 is a factor of xm + 2 for all m. More generally, if A has characteristic p, then x + (p – 1)isa factor of xm + (p − 1) for all m.
4 Prove that if A has characteristic p, then in A[x], (x + c)p = xp + cp. (You may use essentially the same argument as in the proof of Theorem 3, Chapter 20.)
5 Explain why the following “proof of part 4 is not valid: (x + c)p = xp + cp in A[x] because (a + c)p = ap + cp for all a, c ∈ A. (Note the following example: in ![]() 2, a2 + 1 = a4 + 1 for every a, yet x2 + 1 ≠ x4 + 1 in
2, a2 + 1 = a4 + 1 for every a, yet x2 + 1 ≠ x4 + 1 in ![]() 2[x].)
2[x].)
# 6 Use the same argument as in part 4 to prove that if A has characteristic p, then [a(x) + b(x)]p = a(x)p + b(x)p for any a(x), b(x) ∈ A[x]. Use this to prove:
![]()
E. Subrings and Ideals in A[x]
1 Show that if B is a subring of A, then B[x] is a subring of A[x].
2 If B is an ideal of A, B[x] is an ideal of A[x].
3 Let S be the set of all the polynomials a(x) in A[x] for which every coefficient ai for odd i is equal to zero. Show that S is a subring of A[x]. Why is the same not true when “odd” is replaced by “even”?
4 Let J consist of all the elements in A[x] whose constant coefficient is equal to zero. Prove that J is an ideal of A[x].
# 5 Let J consist of all the polynomials a0 + a1x + ⋯ + anxn in A[x] such that a0 + a1 + ⋯ + an = 0. Prove that J is an ideal of A[x].
6 Prove that the ideals in both parts 4 and 5 are prime ideals. (Assume A is an integral domain.)
F. Homomorphisms of Domains of Polynomials
Let A be an integral domain.
1 Let h : A[x]→ A map every polynomial to its constant coefficient; that is,
h(a0 + a1x + ⋯ + anxn) = a0
Prove that h is a homomorphism from A[x] onto A, and describe its kernel.
2 Explain why the kernel of h in part 1 consists of all the products xa(x), for all a(x) ∈ A[x]. Why is this the same as the principal ideal ⟨x⟩ in A[x]?
3 Using parts 1 and 2, explain why A[x]/⟨x⟩ ≅ A.
4 Let g : A[x] → A send every polynomial to the sum of its coefficients. Prove that g is a surjective homomorphism, and describe its kernel.
5 If c ∈ A, let h : A[x] → A[x] be defined by h(a(x)) = a(cx), that is,
h(a0 + a1x + ⋯ + anxn) = a0 + a1cx + a2c2x2 + ⋯ + ancnxn
Prove that h is a homomorphism and describe its kernel.
6 If h is the homomorphism of part 5, prove that h is an automorphism (isomorphism from A[x] to itself) iff c is invertible.
G. Homomorphisms of Polynomial Domains Induced by a Homomorphism of the Ring of Coefficients
Let A and B be rings and let h : A → B be a homomorphism with kernel K. Define ![]() : A[x] → B[x] by
: A[x] → B[x] by
![]() (a0 + a1x + ⋯ + anxn) = h(a0) + h(a1)x + ⋯ + h(an)xn
(a0 + a1x + ⋯ + anxn) = h(a0) + h(a1)x + ⋯ + h(an)xn
(We say that ![]() is induced by h.)
is induced by h.)
1 Prove that ![]() is a homomorphism from A[x] to B[x].
is a homomorphism from A[x] to B[x].
2 Describe the kernel ![]() of
of ![]() .
.
# 3 Prove that ![]() is surjective iff h is surjective.
is surjective iff h is surjective.
4 Prove that ![]() is injective iff h is injective.
is injective iff h is injective.
5 Prove that if a(x) is a factor of b(x), then ![]() (a(x)) is a factor of
(a(x)) is a factor of ![]() (b{x)).
(b{x)).
6 If h : ![]() →
→ ![]() n is the natural homomorphism, let
n is the natural homomorphism, let ![]() :
: ![]() [x] →
[x] → ![]() n[x] be the homomorphism induced by h. Prove that
n[x] be the homomorphism induced by h. Prove that ![]() (a(x)) = 0 iff n divides every coefficient of a(x).
(a(x)) = 0 iff n divides every coefficient of a(x).
7 Let ![]() be as in part 6, and let n be a prime. Prove that if a(x)b(x) ∈ ker
be as in part 6, and let n be a prime. Prove that if a(x)b(x) ∈ ker ![]() , then either a(x) or b(x) is in ker
, then either a(x) or b(x) is in ker ![]() . (HINT: Use Exercise F2 of Chapter 19.)
. (HINT: Use Exercise F2 of Chapter 19.)
H. Polynomials in Several Variables
A[x1, x2] denotes the ring of all the polynomials in two letters x1 and x2 with coefficients in A. For example, x2 – 2xy + y2 + x − 5 is a quadratic polynomial in ![]() [x, y]. More generally, A[x1, …, xn] is the ring of the polynomials in n letters x1, …, xn with coefficients in A. Formally it is defined as follows: Let A[x1] be denoted by A1; then A1[x2] is A[x1, x2]. Continuing in this fashion, we may adjoin one new letter xi at a time, to get A[x1, …, xn].
[x, y]. More generally, A[x1, …, xn] is the ring of the polynomials in n letters x1, …, xn with coefficients in A. Formally it is defined as follows: Let A[x1] be denoted by A1; then A1[x2] is A[x1, x2]. Continuing in this fashion, we may adjoin one new letter xi at a time, to get A[x1, …, xn].
1 Prove that if A is an integral domain, then A[x1, …, xn] is an integral domain.
2 Give a reasonable definition of the degree of any polynomial p(x, y) in A[x, y] and then list all the polynomials of degree ≤ 3 in Z3[x, y].
Let us denote an arbitrary polynomial p(x, y) in A[x, y] by Σ aijxiyj where Σ ranges over some pairs i, j of nonnegative integers.
3 Imitating the definitions of sum and product of polynomials in A[x], give a definition of sum and product of polynomials in A[x, y].
4 Prove that deg a(x, y)b(x, y) = deg a(x, y) + deg b(x, y) if A is an integral domain.
I. Fields of Polynomial Quotients
Let A be an integral domain. By the closing part of Chapter 20, every integral domain can be extended to a “field of quotients.” Thus, A[x] can be extended to a field of polynomial quotients, which is denoted by A(x). Note that A(x) consists of all the fractions a(x)/b(x) for a(x) and b(x) ≠ 0 in A[x], and these fractions are added, subtracted, multiplied, and divided in the customary way.
1 Show that A(x) has the same characteristic as A.
2 Using part 1, explain why there is an infinite field of characteristic p, for every prime p.
3 If A and B are integral domains and h : A → B is an isomorphism, prove that h determines an isomorphism ![]() : A(x) → B(x).
: A(x) → B(x).
J. Division Algorithm: Uniqueness of Quotient and Remainder
In the division algorithm, prove that q(x) and r(x) are uniquely determined. [HINT: Suppose a(x) = b(x)q1(x) + r1(x) = b(x)q2(x) + r2(x), and subtract these two expressions, which are both equal to a(x).]