A Book of Abstract Algebra, Second Edition (1982)

Chapter 30. RULER AND COMPASS

The ancient Greek geometers considered the circle and straight line to be the most basic of all geometric figures, other figures being merely variants and combinations of these basic ones. To understand this view we must remember that construction played a very important role in Greek geometry: when a figure was defined, a method was also given for constructing it. Certainly the circle and the straight line are the easiest figures to construct, for they require only the most rudimentary of all geometric instruments: the ruler and the compass. Furthermore, the ruler, in this case, is a simple, unmarked straightedge.

Rudimentary as these instruments may be, they can be used to carry out a surprising variety of geometric constructions. Lines can be divided into any number of equal segments, and any angle can be bisected. From any polygon it is possible to construct a square having the same area, or twice or three times the area. With amazing ingenuity, Greek geometers devised ways to cleverly use the ruler and compass, unaided by any other instrument, to perform all kinds of intricate and beautiful constructions. They were so successful that it was hard to believe they were unable to perform three little tasks which, at first sight, appear to be very simple: doubling the cube, trisecting any angle, and squaring the circle. The first task demands that a cube be constructed having twice the volume of a given cube. The second asks that any angle be divided into three equal parts. The third requires the construction of a square whose area is equal to that of a given circle. Remember, only a ruler and compass are to be used!

Mathematicians, in Greek antiquity and throughout the Renaissance, devoted a great deal of attention to these problems, and came up with many brilliant ideas. But they never found ways of performing the above three constructions. This is not surprising, for these constructions are impossible! Of course, the Greeks had no way of knowing that fact, for the mathematical machinery needed to prove that these constructions are impossible—in fact, the very notion that one could prove a construction to be impossible—was still two millennia away.

The final resolution of these problems, by proving that the required constructions are impossible, came from a most unlikely source: it was a by-product of the arcane study of field extensions, in the upper reaches of modern algebra.

To understand how all this works, we will see how the process of ruler-and-compass constructions can be placed in the framework of field theory. Clearly, we will be making use of analytic geometry.

If is any set of points in the plane, consider operations of the following two kinds:

1.Ruler operation: Through any two points in , draw a straight line.

2.Compass operation: Given three points A, B, and C in , draw a circle with center C and radius equal in length to the segment AB.

The points of intersection of any two of these figures (line-line, line-circle, or circle-circle) are said to be constructible in one step from . A point P is called constructible from if there are points P₁, P₂, …, P_n = P such that P₁ is constructible in one step from , P₂ is constructible in one step from , and so on, so that P_i is constructible in one step from .

As a simple example, let us see that the midpoint of a line segment AB is constructible from the two points A and B in the above sense. Well, given A and B, first draw the line AB. Then, draw the circle with center A and radius and the circle with center A and radius ; let C and D be the points of intersection of these circles. C and D are constructible in one step from {A, B}. Finally, draw the line through C and D; the intersection of this line with AB is the required midpoint. It is constructible from {A, B}.

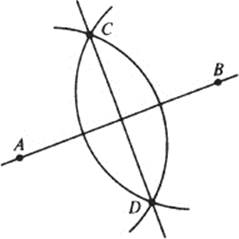
As this example shows, the notion of constructible points is the correct formalization of the intuitive idea of ruler-and-compass constructions.

We call a point in the plane constructible if it is constructible from × , that is, from the set of all points in the plane with rational coefficients.

How does field theory fit into this scheme? Obviously by associating with every point its coordinates. More exactly, with every constructible point P we associate a certain field extension of , obtained as follows:

Suppose P has coordinates (a, b) and is constructed from × in one step. We associate with P the field (a, b), obtained by adjoining to the coordinates of P. More generally, suppose P is constructible from × in nsteps: there are then n points P₁, P₂, …, P_n = P such that each P_i is constructible in one step from × {P₁, …, P_{i −1}}. Let the coordinates of P₁, …, P_n be (a₁, b₁), …, (a_n, b_n), respectively. With the points P₁, …, P_n we associate fields K₁, …, K_n where K₁ = (a₁, b₁), and for each i > 1,

K_i = K_{i − 1} (a_i,b_i)

Thus, K₁ = (a₁, b₁), K₂ = K₁(a₂, b₂), and so on: beginning with , we adjoin first the coordinates of P₁, then the coordinates of P₂, and so on successively, yielding the sequence of extensions

⊆ K₁ ⊆ K₂ ⊆ · · · ⊆ K_n = K

We call K the field extension associated with the point P.

Everything we will have to say in the sequel follows easily from the next lemma.

Lemma If K₁, …, K_n are as defined previously, then [K_i : K_{i − 1}] = 1,2, or 4.

PROOF: Remember that K_{i − 1} already contains the coordinates of P₁,. . ., P_{i − 1}, and K_i is obtained by adjoining to K_{i − 1} the coordinates x_i, y_i of P_i. But P_i is constructible in one step from × {P₁,. . ., P_{i − 1}}, so we must consider three cases, corresponding to the three kinds of intersection which may produce P_i, namely: line intersects line, line intersects circle, and circle intersects circle.

Line intersects line: Suppose one line passes through the points (a₁, a₂) and (b₁, b₂), and the other line passes through (c₁, c₂) and (d₁, d₂). We may write equations for these lines in terms of the constants a₁, a₂, b₁, b₂, c₁, c₂and d₁, d₂ (all of which are in K_{i − 1}), and then solve these equations simultaneously to give the coordinates x, y of the point of intersection. Clearly, these values of x and y are expressed in terms of a₁, a₂, b₁, b₂, c₁, c₂, d₁, d₂, hence are still in K_{i − 1}. Thus, K_i, = K_{i − 1}.

Line intersects circle: Consider the line AB and the circle with center C and radius equal to the distance . Let A, B, C have coordinates (a₁, a₂), (b₁, b₂), and (c₁, c₂), respectively. By hypothesis, K_{i − 1} contains the numbers a₁, a₂, b₁, b₂, c₁, c₂, as well as k² = the square of the distance . (To understand the last assertion, remember that K_{i − 1} contains the coordinates of D and E; see the figure and use the Pythagorean theorem.)

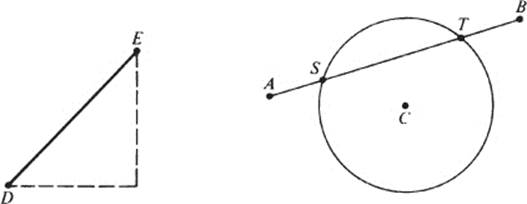
Now, the line AB has equation

and the circle has equation

(x − c₁)² + (y − c₂)² = k² (2)

Solving for x in (1) and substituting into (2) gives

This is obviously a quadratic equation, and its roots are the x coordinates of S and T. Thus, the x coordinates of both points of intersection are roots of a quadratic polynomial with coefficients in K_{i − 1}. The same is true of the ycoordinates. Thus, if K_i = K_{i − 1}(x_i, y_i) where (x_i, y_i) is one of the points of intersection, then

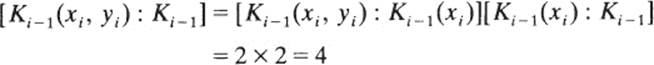
{This assumes that x_i, y_i, ∉ K_{i − 1}. If either x_i or y_i, or both are already in K_{i − 1}, then [K_{i − 1},(x_i, y_i) : K_{i − 1}] = 1 or 2.}

Circle intersects circle: Suppose the two circles have equations

x² + y² + ax + by + c = 0 (3)

and

x² + y² + dx + ey + f = 0 (4)

Then both points of intersection satisfy

(a − d)x + (b − e)y + (c − f) = 0 (5)

obtained simply by subtracting (4) from (3). Thus, x and y may be found by solving (4) and (5) simultaneously, which is exactly the preceding case. ■

We are now in a position to prove the main result of this chapter:

Theorem 1: Basic theorem on constructible points If the point with coordinates (a, b) is constructible, then the degree of (a) over is a power of 2, and likewise for the degree of (b) over .

PROOF: Let P be a constructible point; by definition, there are points P₁. . ., P_n with coordinates (a₁, b₁), …, (a_n, b_n) such that each P_i is constructible in one step from × {P₁,..., P_{i − 1}}, and P_n = P. Let the fields associated with P₁,. . ., P_n be K₁,. . ., K_n. Then

[K_n : ] = [K_n : K_{n − 1}] [K_{n − 1} : K_{n − 2}] ⋯ [K₁ : ]

and by the preceding lemma this is a power of 2, say 2^m. But

[K_n : ] = [K_n : (a)][(a):]

hence[(a) : ] is a factor of 2^m, hence also a power of 2. ■

We will now use this theorem to prove that ruler-and-compass constructions cannot possibly exist for the three classical problems described in the opening to this chapter.

Theorem 2 “Doubling the cube” is impossible by ruler and compass.

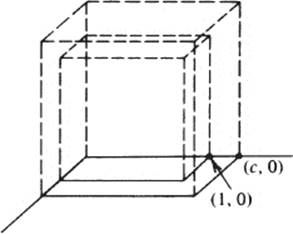
PROOF: Let us place the cube on a coordinate system so that one edge of the cube coincides with the unit interval on the x axis. That is, its endpoints are (0,0) and (1,0). If we were able to double the cube by ruler and compass, this means we could construct a point (c, 0) such that c³ = 2. However, by Theorem 1, [(c) : ] would have to be a power of 2, whereas in fact it is obviously 3. This contradiction proves that it is impossible to double the cube using only a ruler and compass. ■

Theorem 3 “Trisecting the angle” by ruler and compass is impossible. That is, there exist angles which cannot be trisected using a ruler and compass.

PROOF: We will show specifically that an angle of 60° cannot be trisected. If we could trisect an angle of 60°, we would be able to construct a point (c, 0) (see figure) where c = cos 20°; hence certainly we could construct (b,0) where b =2 cos 20°.

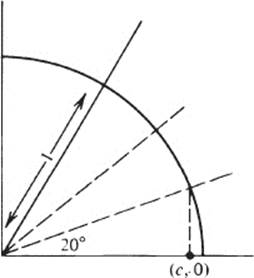
But from elementary trigonometry

cos 3θ = 4 cos³ θ − 3 cos θ

hence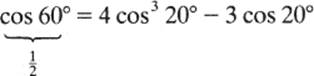

Thus, b = 2 cos 20° satisfies b³ − 3b − 1 = 0. The polynomial

p(x) = x³ − 3x − 1

is irreducible over because p(x + 1) = x³ + 3x² − 3 is irreducible by Eisenstein’s criterion. It follows that (b) has degree 3 over , contradicting the requirement (in Theorem 1) that this degree has to be a power of 2. ■

Theorem 4 “Squaring the circle” by ruler and compass is impossible.

PROOF. If we were able to square the circle by ruler and compass, it would be possible to construct the point ; hence by Theorem 1, would be a power of 2. But it is well known that π is transcendental over . By Theorem 3 of Chapter 29, the square of an algebraic element is algebraic; hence is transcendental. It follows that is not even a finite extension of , much less an extension of some degree 2^m as required. ■

EXERCISES

† A. Constructible Numbers

If O and I are any two points in the plane, consider a coordinate system such that

the interval OI coincides with the unit interval on the x axis. Let be the set of real numbers such that iff the point (a, 0) is constructible from {O, I}. Prove the following:

1 If , then and .

2 If , then . (HINT: Use similar triangles. See the accompanying figure.)

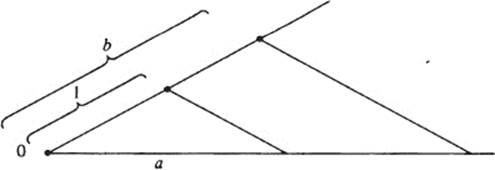
3 If , then . (Use the same figure as in part 2.)

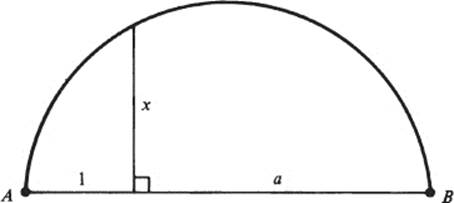
4 If a > 0 and , then . (HINT: In the accompanying figure, AB is the diameter of a circle. Use an elementary property of chords of a circle to show that .)

It follows from parts 1 to 4 that is a field, closed with respect to taking square roots of positive numbers. is called the field of constructible numbers.

5 .

6 If a is a real root of any quadratic polynomial with coefficients in , then . (HINT: Complete the square and use part 4.)

† B. Constructible Points and Constructible Numbers

Prove each of the following:

1 Let be any set of points in the plane; (a, b) is constructible from iff (a, 0) and (0, b) are constructible from .

2 If a point P is constructible from {O,I} [that is, from (0, 0) and (1, 0)], then P is constructible from × .

# 3 Every point in × is constructible from {O, I}. (Use Exercise A5 and the definition of .)

4 If a point P is constructible from × , it is constructible from {O, I}.

By combining parts 2 and 4, we get the following important fact: Any point P is constructible from × iff P is constructible from {O,I}. Thus, we may define a point to be constructible iff it is constructible from {O, I}.

5 A point P is constructible iff both its coordinates are constructible numbers.

† C. Constructible Angles

An angle α is called constructible iff there exist constructible points A, B, and C such that ∠LABC= α. Prove the following:

1 The angle α is constructible iff sin α and cos α are constructible numbers.

2 cos iff sin .

3 If cos α, cos , then cos (α + ß), cos .

4 cos iff cos .

5 If α and β are constructible angles, so are , and nα for any positive integer n.

# 6 The following angles are constructible: .

7 The following angles are not constructible: 20°; 40°, 140°. (HINT: Use the proof of Theorem 3.)

D. Constructible Polygons

A polygon is called constructible iff its vertices are constructible points. Prove the following:

# 1 The regular n-gon is constructible iff the angle 2π/n is constructible.

2 The regular hexagon is constructible.

3 The regular polygon of nine sides is not constructible.

† E. A Constructible Polygon

We will show that 2π/5 is a constructible angle, and it will follow that the regular pentagon is constructible.

1 If r = cos k + i sin k is a complex number, prove that 1/r = cos k − i sin k. Conclude that r + 1/r = 2 cos k.

By de Moivre’s theorem,

is a complex fifth root of unity. Since

x⁵ − 1 = (x − 1)(x⁴ + x³ + x² + x + 1)

ω is a root of p(x) = x⁴ + x³ + x² + x + 1.

2 Prove that ω² + ω + 1 + ω⁻¹ + ω⁻² = 0.

3 Prove that

(HINT: Use parts 1 and 2.) Conclude that cos (2π/5) is a root of the quadratic 4x² − 2x − 1.

4 Use part 3 and A6 to prove that cos (2π/5) is a constructible number.

5 Prove that 2π/5 is a constructible angle.

6 Prove that the regular pentagon is constructible.

† F. A Nonconstructible Polygon

By de Moivre’s theorem,

is a complex seventh root of unity. Since

x⁷ − 1 = (x − 1)(x⁶ + x⁵ + x⁴ + x³ + x² + x + 1)

ω is a root of x⁶ + x⁵ + x⁴ + x³ + x² + x + 1.

1 Prove that ω³ + ω² + ω + 1 + ω⁻¹ + ω⁻² + ω⁻³ = 0.

2 Prove that

(Use part 1 and Exercise El.) Conclude that cos (2π/7) is a root of 8x³ + 4x² − 4x− 1.

3 Prove that 8x³ + 4x² − 4x − 1 has no rational roots. Conclude that it is irreducible over .

4 Conclude from part 3 that cos (2π/7) is not a constructible number.

5 Prove that 2π/7 is not a constructible angle.

6 Prove that the regular polygon of seven sides is not constructible.

G. Further Properties of Constructible Numbers and Figures

Prove each of the following:

1 If the number a is a root of an irreducible polynomial p(x) ∈ [x] whose degree is not a power of 2, then a is not a constructible number.

# 2 Any constructible number can be obtained from rational numbers by repeated addition, subtraction, multiplication, division, and taking square roots of positive numbers.

3 is the smallest field extension of closed with respect to square roots of positive numbers (that is, any field extension of closed with respect to square roots contains ). (Use part 2 and Exercise A.)

4 All the roots of the polynomial x⁴ − 3x² + 1 are constructible numbers.

A line is called constructible if it passes through two constructible points. A circle is called constructible if its center and radius are constructible.

5 The line ax + by + c = 0 is constructible if .

6 The circle x² + y² + ax + by + c = 0 is constructible if .