A Book of Abstract Algebra, Second Edition (1982)

Chapter 33. SOLVING EQUATIONS BY RADICALS

In this final chapter, Galois theory will be used explicitly to answer practical questions about solving equations.

In the introduction to this book we saw that classical algebra was devoted largely to finding methods for solving polynomial equations. The quadratic formula yields the solutions of every equation of degree 2, and similar formulas have been found for polynomials of degrees 3 and 4. But every attempt to find explicit formulas, of the same kind as the quadratic formula, which would solve a general equation of degree 5 or higher ended in failure. The reason for this was finally discovered by the young Galois, who showed that an equation is solvable by the kind of explicit formula we have in mind if and only if its group of symmetries has certain properties. The group of symmetries is, of course, the Galois group which we have already defined, and the required group properties will be formulated in the next few pages.

Galois showed that the groups of symmetries of all equations of degree ≤4 have the properties needed for solvability, whereas equations of degree 5 or more do not always have them. Thus, not only is the classical quest for radical formulas to solve all equations of degree > 4 shown to be futile, but a criterion is made available to test any equation and determine if it has solutions given by a radical formula. All this will be made clear in the following pages.

Every quadratic equation ax² + bx + c = 0 has its roots given by the formula

Equations of degree 3 and 4 can be solved by similar formulas. For example, the cubic equation x³ + ax + b = 0 has a solution given by

Such expressions are built up from the coefficients of the given polynomials by repeated addition, subtraction, multiplication, division, and taking roots. Because of their use of radicals, they are called radical expressions or radical formulas. A polynomial a(x) is solvable by radicals if there is a radical expression giving its roots in terms of its coefficients.

Let us return to the example of x³ + ax + b = 0, where a and b are rational, and look again at Formula (1). We may interpret this formula to assert that if we start with the field of coefficients , adjoin the square root , then adjoin the cube roots , we reach a field in which x³ + ax + b = 0 has its roots.

In general, to say that the roots of a(x) are given by a radical expression is the same as saying that we can extend the field of coefficients of a(x) by successively adjoining nth roots (for various n), and in this way obtain a field which contains the roots of a(x). We will express this notion formally now, in the language of field theory.

F(c₁, …, c_n) is called a radical extension of F if, for each i, some power of c_i is in F(c₁, …, c_{i − 1}). In other words, F(c₁, …, c_n) is an iterated extension of F obtained by successively adjoining nth roots, for various n. We say that a polynomial a(x) in F[x] is solvable by radicals if there is a radical extension of F containing all the roots of a(x), that is, containing the root field of a(x).

To deal effectively with nth roots we must know a little about them. To begin with, the nth roots of 1, called nth roots of unity, are, of course, the solutions of xⁿ − 1 = 0. Thus, for each n, there are exactly n nth roots of unity. As we shall see, everything we need to know about roots will follow from properties of the roots of unity.

In the nth roots of unity are obtained by de Moivre’s theorem. They consist of a number ω and its first n powers: 1 = ω⁰, ω, ω², …, ω^{n − 1}. We will not review de Moivre’s theorem here because, remarkably, the main facts about roots of unity are true in every field of characteristic zero. Everything we need to know emerges from the following theorem:

Theorem 1 Any finite group of nonzero elements in a field is a cyclic group. (The operation in the group is the field’s multiplication.)

PROOF: If F* denotes the set of nonzero elements of F, suppose that G ⊆ F*, and that G, with the field’s “multiply” operation, is a group of n elements. We will compare G with _n and show that G, like _n, has an element of order n and is therefore cyclic.

For any integer k, let g(k) be the number of elements of order k in G, and let z(k) be the number of elements of order k in _n. For every positive integer k which is a factor of n, the equation x^k = 1 has at most k solutions in F; thus,

(*) G contains at most k elements whose order is a factor of k.

If G has an element a of order k, then ⟨a⟩ = {e, a, a², …, a^{k − 1}) are all the distinct elements of G whose order is a factor of k. [By (*), there cannot be any others.] In _n, the subgroup

contains all the elements of _n whose order is a factor of k.

Since ⟨a⟩ and ⟨n/k⟩ are cyclic groups with the same number of elements, they are isomorphic; thus, the number of elements of order k in ⟨a⟩ is the same as the number of elements of order k in ⟨n/k⟩. Thus, g(k) = z(k).

Let us recapitulate: if G has an element of order k, then g(k) = z(k); but if G has no such elements, then g(k) = 0. Thus, for each positive integer k which is a factor of n, the number of elements of order k in G is less than (or equal to) the number of elements of order k in _n.

Now, every element of G (as well as every element of _n) has a well-defined order, which is a divisor of n. Imagine the elements of both groups to be partitioned into classes according to their order, and compare the classes in Gwith the corresponding classes in _n. For each k, G has as many or fewer elements of order k than _n does. So if G had no elements of order n (while _n does have one), this would mean that G has fewer elements than _n, which is false. Thus, G must have an element of order n, and therefore G is cyclic. ■

The nth roots of unity (which are contained in F or a suitable extension of F) obviously form a group with respect to multiplication. By Theorem 1, it is a cyclic group. Any generator of this group is called a primitive nth root of unity. Thus, if ω is a primitive nth root of unity, the set of all the nth roots of unity is

1, ω, ω², …, ω^{n − 1}

If ω is a primitive nth root of unity, F(ω) is an abelian extension of F in the sense that g ∘ h = h ∘ g for any two F-fixing automorphisms g and h of F(ω)). Indeed, any automorphism must obviously send nth roots of unity to nth roots of unity. So if g(ω) = ω^r and h(ω) = ω^s, then g ∘ h(ω) = g(ω^s) = ω^rs and analogously, h ∘ g(ω) = ω^rs. Thus, g ∘ h(ω) = h ∘ g(ω). Since g and h fix F, and every element of F(ω) is a linear combination of powers of ω with coefficients in F, g ∘ h = h ∘ g.

Now, let F contain a primitive nth root of unity, and therefore all the nth roots of unity. Suppose a ∈ F, and a has an nth root b in F. It follows, then, that all the nth roots of a are in F, for they are b, bω, bω², …, bω^{n − 1}. Indeed, if c is any other nth root of a, then clearly c/b is an nth root of 1, say ω^r; hence c = bω⁴. We may infer from the above that if F contains a primitive nth root of unity, and b is an nth root of a, then F(b) is the root field of xⁿ − a over F.

In particular, F(b) is an abelian extension of F. Indeed, any F-fixing automorphism of F(b) must send nth roots of a to nth roots of a: for if c is any nth root of a and g is an F-fixing automorphism, then g(c)ⁿ = g(cⁿ) = g(a) = a; hence g(c) is an nth root of a. So if g(b) = bω^r and h(b) = bω^s, then

g ∘ h(b) = g(bω^s) = bω^rω^s = bω^{r + s}

and

h ∘ g(b) = h(bω^r) = bω^sω^r = bw^{r + s}

hence g ∘ h(b) = h ∘ g(b). Since g and h fix F, and every element in F(b) is a linear combination of powers of b with coefficients in F, it follows that g ∘ h = h ∘ g.

If a(x) is in F[x], remember that a(x) is solvable by radicals just as long as there exists some radical extension of F containing the roots of a(x). [Any radical extension of F containing the roots of a(x) will do.] Thus, we may as well assume that any radical extension used here begins by adjoining to F the appropriate roots of unity; henceforth we will make this assumption. Thus, if K = F(c₁, …, c_n) is a radical extension of F, then

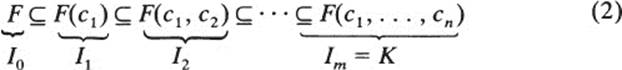
is a sequence of simple abelian extensions. (The extensions are all abelian by the comments in the preceding three paragraphs.)

Still, this is not quite enough for our purposes: In order to use the machinery which was set up in the previous chapter, we must be able to say that each field in (2) is a root field over F. This may be accomplished as follows: Suppose we have already constructed the extensions I₀ ⊆ I₁ ⊆ ⋯ ⊆ I_q in (2) so that I_q is a root field over F. We must extend I_q to I_{q + 1}, so I_{q + 1} is a root field over F. Also, I_{q + 1} must include the element c_{q + 1}, which is the nth root of some element a ∈ I_q.

Let H = {h₁, …, h_r) be the group of all the F-fixing automorphisms of I_q, and consider the polynomial

b(x) = [xⁿ − h₁(a)][xⁿ − h₂(a)] ⋯ [xⁿ − h_r(a)]

By the proof of the lemma on page 327, one factor of b(x) is (xⁿ − a); hence c_{q + 1} is a root of b(x). Moreover, by the same lemma, every coefficient of b(x) is in the fixfield of H, that is, in F. We now define I_{q + 1} to be the root field of b(x) over F. Since all the roots of b(x) are nth roots of elements in I_q, it follows that I_{q + 1} is a radical extension of I_q. The roots may be adjoined one by one, yielding a succession of abelian extensions, as discussed previously. To conclude, we may assume in (2) that K is a root field over F.

If G denotes the Galois group of K over F, each of these fields I_k has a fixer which is a subgroup of G. These fixers form a sequence

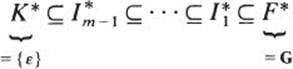
For each k, by Theorem 4 of Chapter 32, is a normal subgroup of , and ≅ Gal(I_{k + 1}: I_k which is abelian because is an abelian extension of I_k. The following definition was invented precisely to account for this situation.

A group G is called solvable if it has a sequence of subgroups {e} = H₀ ⊆ H₁ ⊆ ⋯ ⊆ H_m = G such that for each k, G_k is a normal subgroup of G_{k + 1} and G_{k + 1}/G_k is abelian.

We have shown that if K is a radical extension of F, then Gal(K: F) is a solvable group. We wish to go further and prove that if a(x) is any polynomial which is solvable by radicals, its Galois group is solvable. To do so, we must first prove that any homomorphic image of a solvable group is solvable. A key ingredient of our proof is the following simple fact, which was explained on page 152: G/H is abelian iff H contains all the products xyx^{− 1}y ^{− 1} for all x and y in G. (The products xyx^{− 1}y^{− 1} are called “commutators” of G.)

Theorem 2 Any homomorphic image of a solvable group is a solvable group.

PROOF: Let G be a solvable group, with a sequence of subgroups

{e) ⊆ H₁ ⊆ ⋯ ⊆ H_m = G

as specified in the definition. Let f: G → X be a homomorphism from G onto a group X. Then f(H₀), f(H₁), …, f(H_m) are subgroups of X, and clearly {e} ⊆ f(H₀) ⊆ f(H₁) ⊆ ⋯ ⊆ f(H_m) = X. For each i we have the following: if f(a)∈ f(H_i) and f(x) ∈ f(H_{i + 1}), then a ∈ H_i and x ∈ H_{i + 1}; hence xax^{− 1} ∈ H_i and therefore f(x)f(a)f(x)^{− 1} ∈ f(H_i). So f(H_i) is a normal subgroup of f(H_{i + 1}). Finally, since H_{i + 1}/H_i is abelian, every commutator xyx^{− 1}y^{− 1} (for all x and y in H_{i + 1}) is in H_i; hence every f(x)f(y)f(x)^{− 1}f(y)^{− 1} is in f(H_i). Thus, f(H_{i + 1})/f(H_i) is abelian. ■

Now we can prove the main result of this chapter:

Theorem 3 Let a(x) be a polynomial over a field F. If a(x) is solvable by radicals, its Galois group is a solvable group.

PROOF: By definition, if K is the root field of a(x), there is an extension by radicals F(c₁, …, c_n) such that F ⊆ K ⊆ F (c₁, …, c_n). It follows by Theorem 4 of Chapter 32 that Gal(F(c₁, …, c_n): F)/Gal(F(c₁, …, c_n): K)≅ Gal(K: F); hence by that theorem, Gal(K: F) is a homomorphic image of Gal(F(c₁, …, c_n): F) which we know to be solvable. Thus, by Theorem 2 Gal(K: F) is solvable. ■

Actually, the converse of Theorem 3 is true also. All we need to show is that, if K is an extension of F whose Galois group over F is solvable, then K may be further extended to a radical extension of F. The details are not too difficult and are assigned as Exercise E at the end of this chapter.

Theorem 3 together with its converse say that a polynomial a(x) is solvable by radicals iff its Galois group is solvable.

We bring this chapter to a close by showing that there exist groups which are not solvable, and there exist polynomials having such groups as their Galois group. In other words, there are unsolvable polynomials. First, here is an unsolvable group:

Theorem 4 The symmetric group S₅ is not a solvable group.

PROOF: Suppose S₅ has a sequence of subgroups

{e} = H₀ ⊆ H₁ ⊆ … ⊆ H_m = S₅

as in the definition of solvable group. Consider the subset of S₅ containing all the cycles (ijk) of length 3. We will show that if H_i contains all the cycles of length 3, so does the next smaller group H_{i − 1}. It would follow in m steps that H₀ = {e} contains all the cycles of length 3, which is absurd.

So let H_i contain all the cycles of length 3 in S₅. Remember that if α and β are in H_i, then their commutator αβα⁻¹β⁻¹ is in H_{i − 1}. But any cycle (ijk) is equal to the commutator

(ilj)(jkm)(ilj)⁻¹(jkm)⁻¹ = (ilj)(jkm)(jli)(mkj) = (ijk)

hence every (ijk) is in H_{i − 1}, as claimed. ■

Before drawing our argument toward a close, we need to know one more fact about groups; it is contained in the following classical result of group theory:

Cauchy’s theorem Let G be a finite group of n elements. If p is any prime number which divides n, then G has an element of order p.

For example, if G is a group of 30 elements, it has elements of orders 2, 3, and 5. To give our proof a trimmer appearance, we will prove Cauchy’s theorem specifically for p = 5 (the only case we will use here, anyway). However, the same argument works for any value of p.

PROOF: Consider all possible 5-tuples (a, b, c, d, k) of elements of G whose product abcdk = e. How many distinct 5-tuples of this kind are there? Well, if we select a, b, c, and d at random, there is a unique k = d⁻¹c⁻¹b⁻¹a⁻¹ in Gmaking abcdk = e. Thus, there are n⁴ such 5-tuples.

Call two 5-tuples equivalent if one is merely a cyclic permutation of the other. Thus, (a, b, c, d, k) is equivalent to exactly five distinct 5-tuples, namely, (a, b, c, d, k), (b, c, d, k, a), (c, d, k, a, b), (d, k, a, b, c) and (k, a, b, c, d). The only exception occurs when a 5-tuple is of the form (a, a, a, a, a) with all its components equal; it is equivalent only to itself. Thus, the equivalence class of any 5-tuple of the form (a, a, a, a, a) has a single member, while all the other equivalence classes have five members.

Are there any equivalence classes, other than {(e, e, e, e, e)}, with a single member? If not, then 5|(n⁴ − 1) [for there are n⁴ 5-tuples under consideration, less (e, e, e, e, e)]; hence n⁴ ≡ 1 (mod 5). But we are assuming that 5|n; hence n⁴ ≡ 0 (mod 5), which is a contradiction.

This contradiction shows that there must be a 5-tuple (a, a, a, a, a) ≠ (e, e, e, e, e) such that aaaaa = a⁵ = e. Thus, there is an element a ∈ G of order 5. ■

We will now exhibit a polynomial in [x] having S₅ as its Galois group (remember that S₅ is not a solvable group).

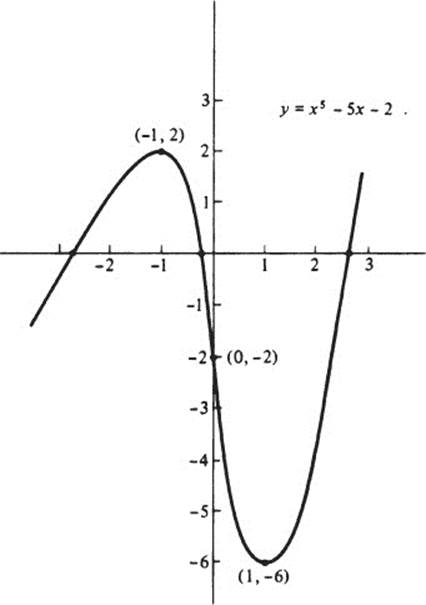
Let a(x) = x⁵ − 5x − 2. By Eisenstein’s criterion, a(x + 2) is irreducible over ; hence a(x) also is irreducible over . By elementary calculus, a{x) has a single maximum at (−1, 2), a single minimum at (1, −6), and a single point of inflection at (0, −2). Thus (see figure), its graph intersects the x axis exactly three times. This means that a(x) has three real roots, r₁, r₂, and r₃, and therefore two complex roots, r₄ and r₅, which must be complex conjugates of each other.

Let K denote the root field of a(x) over , and G the Galois group of a(x). As we have already noted, every element of G may be identified with a permutation of the roots r₁, r₂, r₃, r₄, r₅ of a(x), so G may be viewed as a subgroup of S₅. We will show that G is all of S₅.

Now, [(r₁): ] = 5 because r₁ is a root of an irreducible polynomial of degree 5 over . Since [K: ] = [K: (r₁)][(r₁): ], it follows that 5 is a factor of [K: ]. Then, by Cauchy’s theorem, G contains an element of order 5. This element must be a cycle of length 5: for by Chapter 8, every other element of S₅ is a product of two or more disjoint cycles of length <5, and such products cannot have order 5. (Try the typical cases.) Thus, G contains a cycle of length 5.

Furthermore, G contains a transposition because complex conjugation a + bi → a − bi is obviously a -fixing automorphism of K; it interchanges the complex roots r₄ and r₅ while leaving r₁, r₂, and r₃ fixed.

Any subgroup G ⊆ S₅ which contains a transposition τ and a cycle σ of length 5 necessarily contains all the transpositions. (They are στσ⁻¹, σ²τσ⁻², σ³τσ⁻³, σ⁴τσ⁻⁴, and their products; check this by direct computation!) Finally, if G contains all the transpositions, it contains everything else: for every member of S₅ is a product of transpositions. Thus, G = S₅.

We have just given an example of a polynomial a(x) of degree 5 over whose Galois group S₅ is not solvable. Thus, a(x) is an example of a polynomial of degree 5 which cannot be solved by radicals. In particular, there cannot be a radical formula (on the model of the quadratic formula) to solve all polynomial equations of degree 5, since this would imply that every polynomial equation of degree 5 has a radical solution, and we have just exhibited one which does not have such a solution.

In Exercise B it is shown that S₃, S₄, and all their subgroups are solvable; hence every polynomial of degree ≤4 is solvable by radicals.

EXERCISES

A. Finding Radical Extensions

1 Find radical extensions of containing the following complex numbers:

(a)

(b)

(c)

2 Show that the following polynomials in [x] are not solvable by radicals:

# (a)2x⁵ − 5x⁴ + 5

(b)x⁵ − 4x² + 2

(c)x⁵ − 4x⁴ + 2x + 2

3 Show that a(x) = x⁵ − 10x⁴ + 40x³ − 80x² + 79x − 30 is solvable by radicals over , and give its root field. [HINT: Compute (x − 2)⁵ − (x − 2).]

4 Show that ax⁸ + bx⁶ + cx⁴ + dx² + e is solvable by radicals over any field. (HINT: Let y = x; use the fact that every fourth-degree polynomial is solvable by radicals.)

5 Explain why parts 3 and 4 do not contradict the principal finding of this chapter: that polynomial equations of degree n ≥ 5 do not have a general solution by radicals.

† B. Solvable Groups

Let G be a group. The symbol H G is commonly used as an abbreviation of “H is a normal subgroup of G.” A normal series of G is a finite sequence H₀, H₁, …,H_n of subgroups of G such that

{e} = H₀ H₁ ⋯ H_n = G

Such a series is called a solvable series if each quotient group H_{i + 1}/H_i is abelian. G is called a solvable group if it has a solvable series.

1 Explain why every abelian group is, trivially, a solvable group.

2 Let G be a solvable group, with a solvable series H₀, …, H_n. Let K be a subgroup of G. Show that J₀ = K ∩ H₀, …, J_n = K ∩ H_n is a normal series of K.

# 3 Use the remark immediately preceding Theorem 2 to prove that J₀, …, J_n is a solvable series of K.

4 Use parts 2 and 3 to prove: Every subgroup of a solvable group is solvable.

5 Verify that {ε} ⊆ {ε, β, δ} ⊆ S₃ is a solvable series for S₃. Conclude that S₃, and all of its subgroups, are solvable.

6 In S₄, let A₄ be the group of all the even permutations, and let

B = {ε, (12)(34), (13)(24), (14)(23)}

Show that {ε} ⊆ B ⊆ A₄ ⊆ S₄ is a solvable series for S₄. Conclude that S₄ and all its subgroups are solvable.

The next three sets of exercises are devoted to proving the converse of Theorem 3: If the Galois group of a(x) is solvable, then a(x) is solvable by radicals.

† C. pth Roots of Elements in a Field

Let p be a prime number, and ω a primitive pth root of unity in the field F.

1 If d is any root of x^p − a ∈ F[x], show that F(ω, d) is a root field of x^p − a. Suppose x^p − a is not irreducible in F[x].

2 Explain why x^p − a factors in F[x] as x^p − a = p(x)f(x), where both factors have degree ≤2.

# 3 If deg p(x) = m, explain why the constant term of p(x) (let us call it b) is equal to the product of m pth roots of a. Conclude that b = ω^kd^m for some k.

4 Use part 3 to prove that b^p = a^m.

5 Explain why m and p are relatively prime. Explain why it follows that there are integers s and t such that sm + tp = 1.

6 Explain why b^sp = a^sm. Use this to show that (b^sa^t)^p = a.

7 Conclude: If x^p − a is not irreducible in F[x], it has a root (namely, b^sa^t) in F.

We have proved: x^p − a either has a root in. F or is irreducible over F.

† D. Another Way of Defining Solvable Groups

Let G be a group. The symbol H G should be read, “H is a normal subgroup of G.” A maximal normal subgroup of G is an H G such that, if H J G, then necessarily J = H or J = G. Prove the following:

1 If G is a finite group, every normal subgroup of G is contained in a maximal normal subgroup.

2 Let f: G → H be a homomorphism. If J H, then f⁻¹(J) < G.

# 3 Let K G. If is a subgroup of G/K, let denote the union of all the cosets which are members of . If G/K, then G. (Use part 2.)

4 If K is a maximal normal subgroup of G, then G/K has no nontrivial normal subgroups. (Use part 3.)

5 If an abelian group G has no nontrivial subgroups, G must be a cyclic group of prime order. (Otherwise, choose some a ∈ G such that ⟨a⟩ is a proper subgroup of G.)

6 If H K G, then G/K is a homomorphic image of G/H.

# 7 Let H G, where G/H is abelian. Then G has subgroups H₀, …, H_q such that H = H₀ H₁ ⋯ H_q = G, where each quotient group H_{i + 1}/H_i is cyclic of prime order.

It follows from part 7 that if G is a solvable group, then, by “filling in gaps, ” G has a normal series in which all the quotient groups are cyclic of prime order. Solvable groups are often defined in this fashion.

E. If Gal(K: F) Is Solvable, K Is a Radical Extension of F

Let K be a finite extension of F, where K is a root field over F, with G = Gal(K: F) a solvable group. As remarked in the text, we will assume that F contains the required roots of unity. By Exercise D, let H₀, …, H_n be a solvable series for G in which every quotient H_{i + 1}/H_i is cyclic of prime order. For any i = 1, …, n, let F_i. and F_{i + 1} be the fixfields of H_i and H_{i + 1}.

1 Prove: F_i is a normal extension of F_{i + 1}, and [F_i: F_{i + 1}] is a prime p.

2 Let π be a generator of Gal(F_i: F_{i + 1}), ω a pth root of unity in F_{i + 1}, and b ∈ F_i. Set

c = b + ωπ⁻¹(b) + ω²π⁻²(b) + ⋯ + ω^{p − 1}π^{−(p − 1)}(b)

Show that π(c) = ωc.

3 Use part 2 to prove that π^k(c^p) = c^p for every k, and deduce from this that c^p ∈ F_{i + 1}

4 Prove that F_i is the root field of x^p − c^p over F_{i + 1}.

5 Conclude that K is a radical extension of F.