A Book of Abstract Algebra, Second Edition (1982)
Chapter 4. ELEMENTARY PROPERTIES OF GROUPS
Is it possible for a group to have two different identity elements? Well, suppose e1 and e2 are identity elements of some group G. Then
|
e1 * e2 = e2 |
because e1 is an identity element, and |
|
e1 * e2 = e1 |
because e2 is an identity element |
Therefore
e1 = e2
This shows that in every group there is exactly one identity element.
Can an element a in a group have two different inverses! Well, if a1 and a2 are both inverses of a, then
a1 * (a * a2) = a1* e = a1
and
(a1 * a)*a2 = e*a2 = a2
By the associative law, a1 * (a * a2) = (a1 * a) * a) * a2; hence a1 = a2. This shows that in every group, each element has exactly one inverse.
Up to now we have used the symbol * to designate the group operation. Other, more commonly used symbols are + and · (“plus” and “multiply”). When + is used to denote the group operation, we say we are using additive notation, and we refer to a + b as the sum of a and b. (Remember that a and b do not have to be numbers and therefore “sum” does not, in general, refer to adding numbers.) When · is used to denote the group operation, we say we are using multiplicative notation’, we usually write ab instead of a-b, and call ab the product of a and b. (Once again, remember that “product” does not, in general, refer to multiplying numbers.) Multiplicative notation is the most popular because it is simple and saves space. In the remainder of this book multiplicative notation will be used except where otherwise indicated. In particular, when we represent a group by a letter such as G or H, it will be understood that the group’s operation is written as multiplication.
There is common agreement that in additive notation the identity element is denoted by 0, and the inverse of a is written as −a. (It is called the negative of a.) In multiplicative notation the identity element is e and the inverse of a is written as a−1 (“a inverse”). It is also a tradition that + is to be used only for commutative operations.
The most basic rule of calculation in groups is the cancellation law, which allows us to cancel the factor a in the equations ab = ac and ab = ca. This will be our first theorem about groups.
Theorem 1 If G is a group and a, b, c are elements of G, then
(i) ab = acimpliesb = c and
(ii) ba = caimpliesb = c
It is easy to see why this is true: if we multiply (on the left) both sides of the equation ab = ac by a−1, we get b = c. In the case of ba = ca, we multiply on the right by a−1. This is the idea of the proof; now here is the proof:
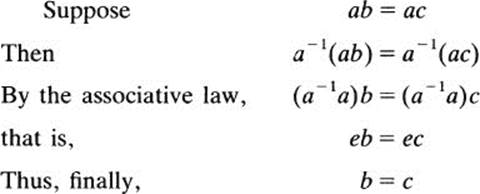
Part (ii) is proved analogously.
In general, we cannot cancel a in the equation ab = ca. (Why not?)
Theorem 2 If G is a group and a, b are elements of G, then
ab=eimpliesa=b−1andb = a−l
The proof is very simple: if ab = e, then ab = aa−1 so by the cancellation law, b = a−1. Analogously, a = b−l.
This theorem tells us that if the product of two elements is equal to e, these elements are inverses of each other. In particular, if a is the inverse of b, then b is the inverse of a.
The next theorem gives us important information about computing inverses.
Theorem 3 If G is a group and a, b are elements of G, then
(i) (ab−1 = b−1a−1and
(ii) (a−1)−1=a
The first formula tells us that the inverse of a product is the product of the inverses in reverse order. The next formula tells us that a is the inverse of the inverse of a. The proof of (i) is as follows:
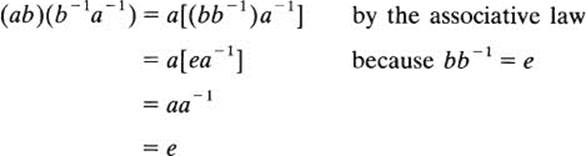
Since the product of ab and b−1a−1 is equal to e, it follows by Theorem 2 that they are each other’s inverses. Thus, (ab)−1 = b−1a−1. The proof of (ii) is analogous but simpler: aa−l = e, so by Theorem 2 a is the inverse of a−1, that is, a= (a−1)−1.
The associative law states that the two products a(bc) and (ab)c are equal; for this reason, no confusion can result if we denote either of these products by writing abc (without any parentheses), and call abc the product of these three elements in this order.
We may next define the product of any four elements a, b, c, and d in G by
abcd = a(bcd)
By successive uses of the associative law we find that
a(bc)d = ab(cd) = (ab)(cd) = (ab)cd
Hence the product abed (without parentheses, but without changing the order of its factors) is defined without ambiguity.
In general, any two products, each involving the same factors in the same order, are equal. The net effect of the associative law is that parentheses are redundant.
Having made this observation, we may feel free to use products of several factors, such as a1a2 ··· an, without parentheses, whenever it is convenient. Incidentally, by using the identity (ab)−l = b−la−l repeatedly, we find that
![]()
If G is a finite group, the number of elements in G is called the order of G. It is customary to denote the order of G by the symbol
|G|
EXERCISES
Remark on notation In the exercises below, the exponential notation an is used in the following sense: if a is any element of a group G, then a2 means aa, a3 means aaa, and, in general, a1 is the product of n factors of a, for any positive integer n.
A. Solving Equations in Groups
Let a, b, c, and x be elements of a group G. In each of the following, solve for x in terms of a, b, and c.
Example Solve simultaneously: x2 =b and x5 = e
From the first equation, b = x2
Squaring, b2 = x4
Multiplying on the left by x, xb2 = xx4 = x5 = e. (Note: x5 = e was given.)
Multiplying by (b2)−1,xb2(b2)−1. Therefore, x = (b2)−1.
Solve:
1 axb = c
2 x2b = xa−1c
Solve simultaneously:
# 3 x2a = bxc−1 and acx = xac
4 ax2 = b and x3 = e
5 x2 = a2andx5 = e
6 (xax)3 = bxand x2a = (xa)−l
B. Rules of Algebra in Groups
For each of the following rules, either prove that it is true in every group G, or give a counterexample to show that it is false in some groups. (All the counterexamples you need may be found in the group of matrices {I, A, B, C, D, K} described on page 28.)
1 If x2 = e, then x = e.
2 If x2 = a2, then x = a.
3 (ab)2 = a2b2
4 If x2 = x, then x = e.
5 For every x ∈ G, there is some y ∈ G such that x = y2. (This is the same as saying that every element of G has a “square root.”)
6 For any two elements x and y in G, there is an element z in G such that y = xz.
C. Elements That Commute
If a and b are in G and ab = ba, we say that a and b commute. Assuming that a and b commute, prove the following:
# 1 a−1 and b−1 commute.
2 a and b−1 commute. (HINT: First show that a = b−1ab.)
3 a commutes with ab.
4 a2 commutes with b2.
5 xax−1 commutes with xbx−1, for any x ∈ G.
6 ab = ba iff aba∈1 = b.
(The abbreviation iff stands for “if and only if.” Thus, first prove that if ab = ba, then aba−1 = b. Next, prove that if aba−1 = b, then ab = ba. Proceed roughly as in Exercise A. Thus, assuming ab = ba, solve for b. Next, assuming aba−1 = b, solve for ab.)
7 ab = baiffaba−1b−1 = e.
† D. Group Elements and Their Inverses1
Let G be a group. Let a, b, c denote elements of G, and let e be the neutral element of G.
1 Prove that if ab = e, then ba = e. (HINT: See Theorem 2.)
# 2 Prove that if abc = e, then cab = e and bca = e.
3 State a generalization of parts 1 and 2
Prove the following:
4 If xay = a−1, then yax = a−1.
5 Let a, b, and c each be equal to its own inverse. If ab = c, then bc = a and ca = b.
6 If abc is its own inverse, then bca is its own inverse, and cab is its own inverse.
7 Let a and b each be equal to its own inverse. Then ba is the inverse of ab.
8 a = a−1iffaa = e. (That is, a is its own inverse iff a2 = e.)
9 Let c = c−1. Thenab = c iffxy2 abc = e.
† E. Counting Elements and Their Inverses
Let G be a finite group, and let S be the set of all the elements of G which are not equal to their own inverse. That is, S = {x ∈ G : x ≠ x−1}. The set S can be divided up into pairs so that each element is paired off with its own inverse. (See diagram on the next page.) Prove the following:
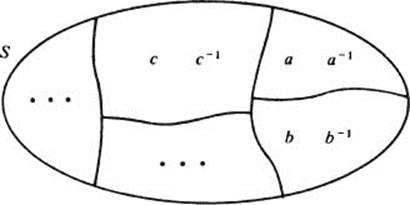
1 In any finite group G, the number of elements not equal to their own inverse is an even number.
2 The number of elements of G equal to their own inverse is odd or even, depending on whether the number of elements in G is odd or even.
3 If the order of G is even, there is at least one element x in G such that x ≠e and x = x−1.
In parts 4 to 6, let G be a finite abelian group, say, G = {e, a1, a2,…, an}. Prove the following:
4 (a1a2 ⋯ an)2 = e
5 If there is no element x ≠ e in G such that x = x−1, then a1a2 ⋯ an = e.
6 If there is exactly one x ≠ e in G such that x = x−1, then a1a2 ⋯ an = x.
† F. Constructing Small Groups
In each of the following, let G be any group. Let e denote the neutral element of G.
1 If a, b are any elements of G, prove each of the following:
(a) If a2 = a, then a = e.
(b) If ab = a, then b = e.
(c) If ab = b, then a = e.
2 Explain why every row of a group table must contain each element of the group exactly once. (HINT: Suppose jc appears twice in the row of a:
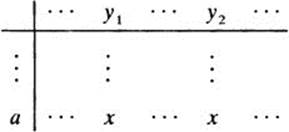
Now use the cancellation law for groups.)
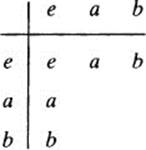
3 There is exactly one group on any set of three distinct elements, say the set {e, a, b}. Indeed, keeping in mind parts 1 and 2 above, there is only one way of completing the following table. Do so! You need not prove associativity.
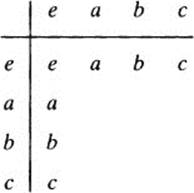
4 There is exactly one group G of four elements, say G = {e, a, b, c}, satisfying the additional property that xx = e for every x ∈ G. Using only part 1 above, complete the following group table of G:
5 There is exactly one group G of four elements, say G = {e, a, b, c}, such that xx = e for some x ≠ e in G, and yy ≠ e for some y ∈ G (say, aa = e and bb ≠ e). Complete the group table of G, as in the preceding exercise.
6 Use Exercise E3 to explain why the groups in parts 4 and 5 are the only possible groups of four elements (except for renaming the elements with different symbols).
G. Direct Products of Groups
If G and H are any two groups, their direct product is a new group, denoted by G × H, and defined as follows: G × H consists of all the ordered pairs (x, y) where x is in G and y is in H. That is,
G × H = {(x, y) : x ∈ Gandy ∈ H}
The operation of G × H consists of multiplying corresponding components:
(x, y) · (x′ y′) = (xx′, yy′)
If G and H are denoted additively, it is customary to denote G × H additively:
(x, y) + (x′ y′)=(x+x′,y+y′)
1 Prove that G × H is a group by checking the three group axioms, (Gl) to (G3):
(G1) (x1,y1)[(x2,y2)(x3,y3)] = (,)
[(x1,y1)(x2,y2)](x3,y3) = (,)
(G2) Let eG be the identity element of G, and eH the identity element of H.
The identity element of G × H is (,). Check
(G3) For each (a, b) ∈ G × H, the inverse of (a, b) is (,). Check.
2 List the elements of ![]() 2 ×
2 × ![]() 3, and write its operation table. (NOTE: There are six elements, each of which is an ordered pair. The notation is additive.)
3, and write its operation table. (NOTE: There are six elements, each of which is an ordered pair. The notation is additive.)
# 3 If G and H are abelian, prove that G × H is abelian.
4 Suppose the groups G and H both have the following property:
Every element of the group is its own inverse.
Prove that G × H also has this property.
H. Powers and Roots of Group Elements
Let G be a group, and a, b ∈ G. For any positive integer n we define an by
![]()
If there is an element x ∈ G such that a = x2, we say that a has a square root in G. Similarly, if a = y3 for some y ∈ G, we say a has a cube root in G. In general, a has an nth root in G if a = zn for some z ∈ G. Prove the following:
1 (bab−l)n = banb−l, for every positive integer Prove by induction. (Remember that to prove a formula such as this one by induction, you first prove it for n = l; next you prove that if it is true for n = k, then it must be true for n = k + 1. You may conclude that it is true for every positive integer n. Induction is explained more fully in Appendix C.)
2 If ab = ba, then (ab)n = anbn for every positive integer n. Prove by induction.
3 If xax = e, then (xa)2n = an.
4 If a3 = e, then a has a square root.
5 If a2 = e, then a has a cube root.
6 If a∈1 has a cube root, so does a.
7 If x2ax = a−1, then a has a cube root. (HINT: Show that xax is a cube root of a−1.)
8 If xax = b, then 06 has a square root.
1 When the exercises in a set are related, with some exercises building on preceding ones so that they must be done in sequence, this is indicated with a symbol t in the margin to the left of the heading.