A Book of Abstract Algebra, Second Edition (1982)

Chapter 5. SUBGROUPS

Let G be a group, and S a nonempty subset of G. It may happen (though it doesn’t have to) that the product of every pair of elements of S is in S. If it happens, we say that S is closed with respect to multiplication. Then, it may happen that the inverse of every element of S is in S. In that case, we say that S is closed with respect to inverses. If both these things happen, we call S a subgroup of G.

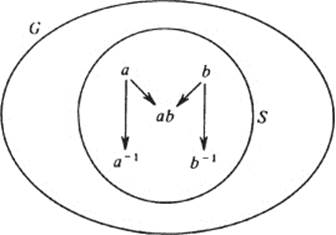
When the operation of G is denoted by the symbol +, the wording of these definitions must be adjusted: if the sum of every pair of elements of S is in S, we say that S is closed with respect to addition. If the negative of every element of S is in S, we say that S is closed with respect to negatives. If both these things happen, S is a subgroup of G.

For example, the set of all the even integers is a subgroup of the additive group of the integers. Indeed, the sum of any two even integers is an even integer, and the negative of any even integer is an even integer.

As another example, * (the group of the nonzero rational numbers, under multiplication) is a subgroup of * (the group of the nonzero real numbers, under multiplication). Indeed, * ⊆ * because every rational number is a real number. Furthermore, the product of any two rational numbers is rational, and the inverse (that is, the reciprocal) of any rational number is a rational number.

An important point to be noted is this: if S is a subgroup of G, the operation of S is the same as the operation of G. In other words, if a and b are elements of S, the product ab computed in S is precisely the product ab computed in G.

For example, it would be meaningless to say that ⟨*, ·⟩ is a subgroup of ⟨, +⟩; for although it is true that * is a subset of , the operations on these two groups are different.

The importance of the notion of subgroup stems from the following fact: if G is a group and S is a subgroup of G, then S itself is a group.

It is easy to see why this is true. To begin with, the operation of G, restricted to elements of S, is certainly an operation on S. It is associative: for if a, b, and c are in S, they are in G (because S ⊆ G); but G is a group, so a(bc) = (ab)c. Next, the identity element e of G is in S (and continues to be an identity element in S) for S is nonempty, so S contains an element a; but S is closed with respect to inverses, so S also contains a^–1; thus, S contains aa^–1 = e, because S is closed with respect to multiplication. Finally, every element of S has an inverse in S because S is closed with respect to inverses. Thus, S is a group!

One reason why the notion of subgroup is useful is that it provides us with an easy way of showing that certain things are groups. Indeed, if G is already known to be a group, and S is a subgroup of G, we may conclude that S is a group without having to check all the items in the definition of “group.” This conclusion is illustrated by the next example.

Many of the groups we use in mathematics are groups whose elements are functions. In fact, historically, the first groups ever studied as such were groups of functions.

() represents the set of all functions from to , that is, the set of all real-valued functions of a real variable. In calculus we learned how to add functions: if f and g are functions from to , their sum is the function f + ggiven by

[f + g](x) = f(x) + g(x) for every real number x

Clearly, f + g is again a function from to , and is uniquely determined by f and g.

(), with the operation + for adding functions, is the group ⟨(),+⟩, or simply (). The details are simple, but first, let us remember what it means for two functions to be equal. If f and g are functions from to , then fand g are equal (that is, f = g) if and only if f(x) = g(x) for every real number x. In other words, to be equal, f and g must yield the same value when applied to every real number x.

To check that + is associative, we must show that f + [g + h] = [f + g] + h, for every three functions, f, g, and h in (). This means that for any real number x, {f + [g + h]}(x) = {[f + g] + h}(x). Well,

{f + [g + h]}(x) = f(x) + [g + h] (x) = f(x) + g(x) + h(x)

and {[f + g] + h}(x) has the same value.

The neutral element of () is the function given by

(x) = 0 for every real number x

To show that + f = f, one must show that [ + f](x) = f(x) for every real number x. This is true because [ + f](x) = (x) + f(x) = 0 + f(x) = f(x).

Finally, the inverse of any function f is the function –f given by

[–f](x) = –f(x) for every real number x

One perceives immediately that f + [–f] = , for every function f.

() represents the set of all continuous functions from to . Now, (), with the operation +, is a subgroup of (), because we know from calculus that the sum of any two continuous functions is a continuous function, and the negative –f of any continuous function f is a continuous function. Because any subgroup of a group is itself a group, we may conclude that (), with the operation +, is a group. It is denoted by ⟨(), +⟩, or simply ().

() represents the set of all the differentiable functions from to . It is a subgroup of () because the sum of any two differentiable functions is differentiable, and the negative of any differentiable function is differentiable. Thus, (), with the operation of adding functions, is a group denoted by ⟨(), +⟩, or simply ().

By the way, in any group G the one-element subset {e}, containing only the neutral element, is a subgroup. It is closed with respect to multiplication because ee = e, and closed with respect to inverses because e^–1 = e. At the other extreme, the whole group G is obviously a subgroup of itself. These two examples are, respectively, the smallest and largest possible subgroups of G. They are called the trivial subgroups of G. All the other subgroups of G are called proper subgroups.

Suppose G is a group and a, b, and c are elements of G. Define S to be the subset of G which contains all the possible products of a, b, c, and their inverses, in any order, with repetition of factors permitted. Thus, typical elements of S would be

abac^–1

c^–1a^–1bbc

and so on. It is easy to see that S is a subgroup of G: for if two elements of S are multiplied together, they yield an element of S, and the inverse of any element of S is an element of S. For example, the product of aba and cb^–1ac is

abacb^–1ac

and the inverse of ab^–1c^–1a is

a^–1cba^–1

S is called the subgroup of G generated by a, b, and c.

If a₁, …, a_n are any finite number of elements of G, we may define the subgroup generated by a₁, …, a_n in the same way. In particular, if a is a single element of G, we may consider the subgroup generated by a. This subgroup is designated by the symbol ⟨a⟩, and is called a cyclic subgroup of G; a is called its generator. Note that ⟨a⟩ consists of all the possible products of a and a⁻¹, for example, a^–1aaa^–1 and aaa^–1aa^–1. However, since factors of a^–1cancel factors of a, there is no need to consider products involving both a and a^–1 side by side. Thus, ⟨a⟩ contains

a, aa, aaa,. . .,

a^–1, a^–1a^–1, a^–1a^–1a¹, …,

as well as aa^–1 = e.

If the operation of G is denoted by +, the same definitions can be given with “sums” instead of “products.”

In the group of matrices whose table appears on page 28, the subgroup generated by D is ⟨D⟩ = {I, B, D} and the subgroup generated by A is ⟨A⟩ = {I, A}. (The student should check the table to verify this.) In fact, the entire group G of that example is generated by the two elements A and B.

If a group G is generated by a single element a, we call G a cyclic group, and write G − ⟨a⟩. For example, the additive group ₆ is cyclic. (What is its generator?)

Every finite group G is generated by one or more of its elements (obviously). A set of equations, involving only the generators and their inverses, is called a set of defining equations for G if these equations completely determine the multiplication table of G.

For example, let G be the group {e, a, b, b², ab, ab²} whose generators a and b satisfy the equations

a² = e b³ = e ba = ab² (1)

These three equations do indeed determine the multiplication table of G. To see this, note first that the equation ba = ab² allows us to switch powers of a with powers of b, bringing powers of a to the left, and powers of b to the right. For example, to find the product of ab and ab², we compute as follows:

But by Equations (1), a² = e and b⁴ = b³b = b; so finally, (ab)(ab²) = b. All the entries in the table of G may be computed in the same fashion.

When a group is determined by a set of generators and defining equations, its structure can be efficiently represented in a diagram called a Cayley diagram. These diagrams are explained in Exercise G.

EXERCISES

A. Recognizing Subgroups

In parts 1–6 below, determine whether or not H is a subgroup of G. (Assume that the operation of H is the same as that of G.)

Instructions If H is a subgroup of G, show that both conditions in the definition of “subgroup” are satisfied. If H is not a subgroup of G, explain which condition fails.

Example G = *, the multiplicative group of the real numbers.

H = {2ⁿ : n ∈ } H is is not □ a subgroup of G.

(i) If 2ⁿ, 2^m ∈ H, then 2ⁿ2^m = 2^n+m. But n + m ∈ , so 2^n+m ∈ H.

(ii) If 2ⁿ ∈ H, then 1/2ⁿ = 2^–n. But –n ∈ , so 2^n+m ∈ H.

(Note that in this example the operation of G and H is multiplication. In the next problem, it is addition.)

1 G = ⟨, +⟩, H = {log a : a ∈ , a > 0}. H is □ is not □ a subgroup of G.

2 G = ⟨, +⟩, H = {log n : n ∈ , n > 0}. H is □ is not □ a subgroup of G.

3 G = ⟨, +⟩, H = {x ∈ : tan x ∈ }. H is □ is not □ a subgroup of G.

HINT: Use the following formula from trigonometry:

4 G = ⟨*, ·⟩, H = {2ⁿ3^m : m, n ∈ }. H is □ is not □ a subgroup of G.

5 G = ⟨ × , +⟩, H = {(x, y) : y = 2x}. H is □ is not □ a subgroup of G.

6 G = ⟨ × , +⟨, H = {(x, y) : x² + y² > 0}. H is □ is not □ a subgroup of G.

7 Let C and D be sets, with C ⊆ D. Prove that P_C is a subgroup of P_D. (See Chapter 3, Exercise C.)

B. Subgroups of Functions

In each of the following, show that H is a subgroup of G.

Example G = ⟨(), +⟩, H = {f ∈ () : f(0) = 0}

(i) Suppose f, g ∈ H; then f(0) = 0 and g(0) = 0, so [f + g](0) = f(0) + g(0) = 0 + 0 = 0. Thus, f + g ∈ H.

(ii) If f ∈ H, then f(0) = 0. Thus, [–f](0) = –f(0) = –0 =0, so –f ∈ H.

1 G = ⟨(), +⟩, H = {f ∈ () : f(x) = 0 for every x ∈ [0,1]}

2 G = ⟨(), +⟩, H = {f ∈ () : f(–x) = –f(x)}

3 G = ⟨(), +⟩, H = {f ∈ () : f is periodic of period π}

REMARK: A function f is said to be periodic of period a if there is a number a, called the period of f, such that f(x) = f(x + na) for every x ∈ and n ∈ .

4 G = ⟨ (), +⟩, H = {f ∈ () :

# 5 G = ⟨(),+⟩, H = {f∈() : df/dx is constant}

6 G = ⟨(),+⟩, H = {f ∈ () : f(x)∈ for every x∈}

C. Subgroups of Abelian Groups

In the following exercises, let G be an abelian group.

1 If H = {x ∈ G : x = x^–1}, that is, H consists of all the elements of G which are their own inverses, prove that H is a subgroup of G.

2 Let n be a fixed integer, and let H = {x ∈ G : xⁿ = e}. Prove that H is a subgroup of G.

3 Let H = {x ∈ G : x = y² for some y ∈ G}; that is, let H be the set of all the elements of G which have a square root. Prove that H is a subgroup of G.

4 Let Hbe a subgroup of G, and let K = {x ∈ G : x² ∈ H}. Prove that K is a subgroup of G.

# 5. Let H be a subgroup of G, and let K consist of all the elements x in G such that some power of x is in H. That is, K = {x ∈ G : for some integer n > 0, xⁿ ∈ H). Prove that K is a subgroup of G.

6 Suppose H and K are subgroups of G, and define HK as follows:

HK = {xy : x ∈ H and y ∈ K}

Prove that HK is a subgroup of G.

7 Explain why parts 4–6 are not true if G is not abelian.

D. Subgroups of an Arbitrary Group

Let G be a group.

1 If H and K are subgroups of a group G, prove that H ∩ K is a subgroup of G. (Remember that x ∈ H ∩ K iff x ∈ H and x ∈ K.)

2 Let H and K be subgroups of G. Prove that if H ⊆ K, then H is a subgroup of K.

3 By the center of a group G we mean the set of all the elements of G which commute with every element of G, that is,

C = {a ∈ G : ax = xa for every x ∈ G)

Prove that C is a subgroup of G.

4 Let C′ = {a ∈ G: (ax)² = (xa)² for every x ∈ G). Prove that C′ is a subgroup of G.

# 5 Let G be a finite group, and let S be a nonempty subset of G. Suppose S is closed with respect to multiplication. Prove that S is a subgroup of G. (HINT: It remains to prove that S contains e and is closed with respect to inverses. Let S = {a₁, …, a_n}. If a_i ∈ S, consider the distinct elements a_ia₁, a_ia₂, …, a_ia_n.)

6 Let G be a group and f : G → G a function. A period of f is any element a in G such that f(x) = f(ax) for every x ∈ G. Prove: The set of all the periods of f is a subgroup of G.

# 7 Let H be a subgroup of G, and let K = {x ∈ G : xax⁻¹ ∈ H iff a ∈ H}. Prove:

(a) K is a subgroup of G.

(b) H is a subgroup of K.

8 Let G and H be groups, and G × H their direct product.

(a) Prove that {(x, e) : x ∈ G} is a subgroup of G × H.

(b) Prove that {(x, x) : x ∈ G} is a subgroup of G × G.

E. Generators of Groups

1 List all the cyclic subgroups of ⟨₁₀, +⟩.

2 Show that ₁₀ is generated by 2 and 5.

3 Describe the subgroup of ₁₂ generated by 6 and 9.

4 Describe the subgroup of generated by 10 and 15.

5 Show that is generated by 5 and 7.

6 Show that ₂ × ₃ is a cyclic group. Show that ₃ × ₄ is a cyclic group.

# 7 Show that ₂ × ₄ is not a cyclic group, but is generated by (1, 1) and (1, 2).

8 Suppose a group G is generated by two elements a and b. If ab = ba, prove that G is abelian.

F. Groups Determined by Generators and Defining Equations

# 1 Let G be the group {e, a, b, b², ab, ab²} whose generators satisfy a² = e, b³ = e, ba = ab². Write the table of G.

2 Let G be the group {e, a, b, b², b³, ab, ab², ab³} whose generators satisfy a² = e, b⁴ = e, ba = ab³. Write the table of G. (G is called the dihedral group D₄.)

3 Let G be the group {e, a, b, b², b³, ab, ab², ab³} whose, generators satisfy a⁴ = e, a² = b², ba = ab³. Write the table of G. (G is called the quaternion group.)

4 Let G be the commutative group {e, a, b, c, ab, be, ac, abc} whose generators satisfy a² = b² = c² = e. Write the table of G.

G. Cayley Diagrams

Every finite group may be represented by a diagram known as a Cayley diagram. A Cayley diagram consists of points joined by arrows.

There is one point for every element of the group.

The arrows represent the result of multiplying by a generator.

For example, if G has only one generator a (that is, G is the cyclic group ⟨a⟩), then the arrow → represents the operation “multiply by a”:

e→a→a²→a³ · · ·

If the group has two generators, say a and b, we need two kinds of arrows, say and →, where means “multiply by a,” and → means “multiply by b.”

For example, the group G = {e, a, b, b², ab, ab²} where a² = e, b³ = e, and ba = ab² (see page 47) has the following Cayley diagram:

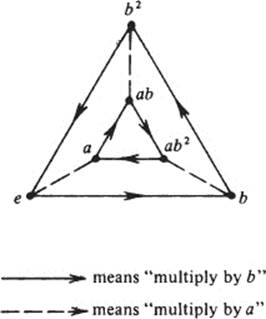
Moving in the forward direction of the arrow → means multiplying by b,

whereas moving in the backward direction of the arrow means multiplying by b^–1:

(Note that “multiplying x by b” is understood to mean multiplying on the right by b: it means xb, not bx.) It is also a convention that if a² = e (hence a = a^–1), then no arrowhead is used:

for if a = a^–1, then multiplying by a is the same as multiplying by a^–1.

The Cayley diagram of a group contains the same information as the group’s table. For instance, to find the product (ab)(ab²) in the figure on page 51, we start at ab and follow the path corresponding to ab² (multiplying by a, then by b, then again by b), which is

This path leads to b; hence (ab)(ab²) = b.

As another example, the inverse of ab² is the path which leads from ab² back to e. We note instantly that this is ba.

A point-and-arrow diagram is the Cayley diagram of a group iff it has the following two properties: (a) For each point x and generator a, there is exactly one a-arrow starting at x, and exactly one a-arrow ending at x; furthermore, at most one arrow goes from x to another point y. (b) If two different paths starting at x lead to the same destination, then these two paths, starting at any point y, lead to the same destination.

Cayley diagrams are a useful way of finding new groups.

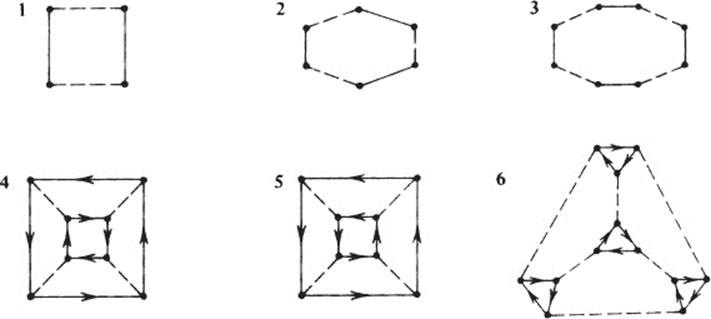
Write the table of the groups having the following Cayley diagrams: (REMARK: You may take any point to represent e, because there is perfect symmetry in a Cayley diagram. Choose e, then label the diagram and proceed.)

H. Coding Theory: Generator Matrix and Parity-Check Matrix of a Code

For the reader who does not know the subject, linear algebra will be developed in Chapter 28. However, some rudiments of vector and matrix multiplication will be needed in this exercise; they are given here:

A vector with n components is a sequence of n numbers: (a₁, a₂, …, a_n). The dot product of two vectors with n components, say the vectors a = (a₁, a₂, …, a_n) and b = (b₁, b₂, …, b_n), is defined by

a · b = (a₁, a₂, …, a_n) · (b₁, b₂, …, b_n) = a₁b₁ + a₂b₂ + · · · + a_nb_n

that is, you multiply corresponding components and add. For example,

(1,4, –2, 3) · (6, 2, 4, –2) = 1(6) + 4(2) + (–2)4 + 3(–2) = 0

When a · b = 0, as in the last example, we say that a and b are orthogonal.

A matrix is a rectangular array of numbers. An “m by n matrix” (m × n matrix) has m rows and n columns. For example,

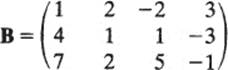
is a 3 × 4 matrix: It has three rows and four columns. Notice that each row of B is a vector with four components, and each column of B is a vector with three components.

If A is any m × n matrix, let a₁, a₂, …, a_n be the columns of A. (Each column of A is a vector with m components.) If x is any vector with m components, xA denotes the vector

xA = (x·a₁, x·a₂, …, x·a_n)

That is, the components of xA are obtained by dot multiplying x by the successive columns of A. For example, if B is the matrix of the previous paragraph and x = (3,1, –2), then the components of xB are

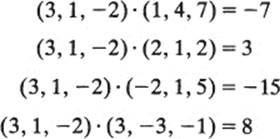
that is, xB = (−7, 3, −15, 8).

If A is an m × n matrix, let a⁽¹⁾, a⁽²⁾, …, a^(m) be the rows of A. If y is any vector with n components, Ay denotes the vector

Ay = (y · a⁽¹⁾, y · a⁽²⁾, …, y · a^(m))

That is, the components of Ay are obtained by dot multiplying y with the successive rows of A. (Clearly, Ay is not the same as yA.) From linear algebra, A(x + y) = Ax + Ay and (A + B)x = Ax + Bx.

We shall now continue the discussion of codes begun in Exercises F and G of Chapter 3. Recall that is the set of all vectors of length n whose entries are 0s and 1s. In Exercise F, page 32, it was shown that is a group. A code is defined to be any subset C of . A code is called a group code if C is a subgroup of . The codes described in Chapter 3, as well as all those to be mentioned in this exercise, are group codes.

An m × n matrix G is a generator matrix for the code C if C is the group generated by the rows of G. For example, if C₁ is the code given on page 34, its generator matrix is

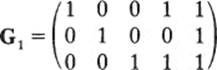
You may check that all eight codewords of C₁ are sums of the rows of G₁.

Recall that every codeword consists of information digits and parity-check digits. In the code C₁ the first three digits of every codeword are information digits, and make up the message; the last two digits are parity-check digits. Encoding a message is the process of adding the parity-check digits to the end of the message. If x is a message, then E(x) denotes the encoded word. For example, recall that in C₁ the parity-check equations are a₄ = a₁ + a₃and a₅ = a₁ + a₂ + a₃. Thus, a three-digit message a₁a₂a₃ is encoded as follows:

E(a₁, a₂, a₃) = (a₁, a₂, a₃, a₁ + a₃, a₁ + a₂ + a₃)

The two digits added at the end of a word are those dictated by the parity check equations. You may verify that

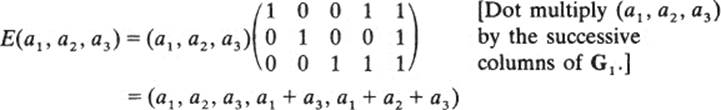
This is true in all cases: If G is the generator matrix of a code and x is a message, then E(x) is equal to the product xG. Thus, encoding using the generator matrix is very easy: you simply multiply the message x by the generator matrix G.

Now, the parity-check equations of C₁ (namely, a₄ = a₁ + a₃ and a₅ = a₁ + a₂ + a₃) can be written in the form

a₁ + a₃ + a₄ = 0 and a₁ + a₂ + a₃ + a₅ = 0

which is equivalent to

(a₁, a₂, a₃, a₄, a₅) · (1, 0, 1, 1, 0) = 0

and

(a₁, a₂, a₃, a₄, a₅) · (1, 1, 1, 0, 1) = 0

The last two equations show that a word a₁a₂a₃a₄a₅ is a codeword (that is, satisfies the parity-check equations) if and only if (a₁, a₂, a₃, a₄, a₅) is orthogonal to both rows of the matrix:

H is called the parity-check matrix of the code C₁. This conclusion may be stated as a theorem:

Theorem 1 Let H be the parity-check matrix of a code C in . A word x in is a codeword if and only if Hx = 0.

(Remember that Hx is obtained by dot multiplying x by the rows of H.)

1 Find the generator matrix G₂ and the parity-check matrix H₂ of the code C₂ described in Exercise G2 of Chapter 3.

2 Let C₃ be the following code in : the first four positions are information positions, and the parity-check equations are a₅ = a₂ + a₃ + a₄, a₆ = a₁ + a₃ + a₄, and a₇ = a₁ + a₂ + a₄. (C₃ is called the Hamming code.) Find the generator matrix G₃ and parity-check matrix H₃ of C₃.

The weight of a word x is the number of Is in the word and is denoted by w(x). For example, w(11011) = 4. The minimum weight of a code C is the weight of the nonzero codeword of smallest weight in the code. (See the definitions of “distance” and “minimum distance” on page 34.) Prove the following:

# 3 d(x, y) = w(x + y).

4 w(x) = d(x, 0), where 0 is the word whose digits are all 0s.

5 The minimum distance of a group code C is equal to the minimum weight of C.

6 (a) If x and y have even weight, so does x + y.

(b) If x and y have odd weight, x + y has even weight.

(c) If x has odd and y has even weight, then x + y has odd weight.

7 In any group code, either all the words have even weight, or half the words have even weight and half the words have odd weight. (Use part 6 in your proof.)

8 H(x + y) = 0 if and only if Hx = Hy, where H denotes the parity-check matrix of a code in and x and y are any two words in ).