A Book of Abstract Algebra, Second Edition (1982)

Chapter 7. GROUPS OF PERMUTATIONS

In this chapter we continue our discussion of functions, but we confine our discussions to functions from a set to itself. In other words, we consider only functions f : A → A whose domain is a set A and whose range is in the same set A.

To begin with, we note that any two functions f and g (from A to A) are equal if and only if f(x) = g(x) for every element x in A.

If f and g are functions from A to A, their composite f ∘ g is also a function from A to A. We recall that it is the function defined by

[f ∘ g](x) = f(g(x)) for every x in A (1)

It is a very important fact that the composition of functions is associative. Thus, if f, g, and h are three functions from A to A, then

f ∘ (g ∘ h) = (f ∘ g) ∘ h

To prove that the functions f ∘ (g ∘ h) and (f ∘ g) ∘ h are equal, one must show that for every element x in A,

{f ∘ [g ∘ h]}(x) = {[f ∘ g] ∘ h}(x)

We get this by repeated use of Equation (1):

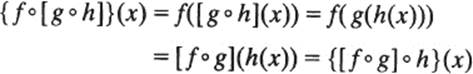
By a permutationof a set A we mean a bijective function from A to A, that is, a one-to-one correspondence between A and itself. In elementary

algebra we learned to think of a permutation as a rearrangement of the elements of a set. Thus, for the set {1,2,3,4,5}, we may consider the rearrangement which changes (1,2,3,4,5) to (3,2,1,5,4); this rearrangement may be identified with the function

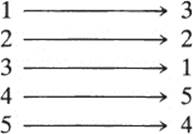
which is obviously a one-to-one correspondence between the set {1,2,3,4,5} and itself. It is clear, therefore, that there is no real difference between the new definition of permutation and the old. The new definition, however, is more general in a very useful way since it allows us to speak of permutations of sets A even when A has infinitely many elements.

In Chapter 6 we saw that the composite of any two bijective functions is a bijective function. Thus, the composite of any two permutations of A is a permutation of A. It follows that we may regard the operation ∘ of composition as an operation on the set of all the permutations of A. We have just seen that composition is an associative operation. Is there a neutral element for composition?

For any set A, the identity function on A, symbolized by ε_A or simply ε, is the function x → x which carries every element of A to itself. That is, it is defined by

ε(x) = x for every element x ∈ A

It is easy to see that ε is a permutation of A (it is a one-to-one correspondence between A and itself); and if f is any other permutation of A, then

f ∘ ε = f and ε ∘ f = f

The first of these equations asserts that [f ∘ ε](x) = f(x) for every element x in A, which is quite obvious, since [f ∘ ε](x)= f(ε(x))= f(x). The second equation is proved analogously.

We saw in Chapter 6 that the inverse of any bijective function exists and is a bijective function. Thus, the inverse of any permutation of A is a permutation of A. Furthermore, if f is any permutation of A and f⁻¹ is its inverse, then

f⁻¹ ∘ f= ε and f ∘ f⁻¹ = ε

The first of these equations asserts that for any element x in A,

[f⁻¹ ∘ f](x) = ε(x)

that is, f⁻¹(f(x)) = x:

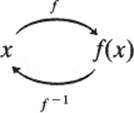
This is obviously true, by the definition of the inverse of a function. The second equation is proved analogously.

Let us recapitulate: The operation ∘ of composition of functions qualifies as an operation on the set of all the permutations of A. This operation is associative. There is a permutation ε such that ε ∘ f = f and f ∘ ε = f for any permutation f of A. Finally, for every permutation f of A there is another permutation f⁻¹ of A such that f ∘ f⁻¹ = ε and f⁻¹ ∘ f = ε. Thus, the set of all the permutations of A, with the operation ∘ of composition, is a group.

For any set A, the group of all the permutations of A is called the symmetric group on A, and it is represented by the symbol S_A. For any positive integer n, the symmetric group on the set {1, 2, 3,. . ., n} is called the symmetric group on η elements, and is denoted by S_n.

Let us take a look at S₃. First, we list all the permutations of the set {1,2,3}:

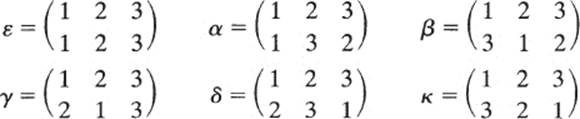
This notation for functions was explained on page 57; for example,

is the function such that β(1) = 3, β(2) = 1, and β(3) = 2. A more graphic way of representing the same function would be

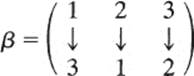
The operation on elements of S₃ is composition. To find α ∘ β, we note that

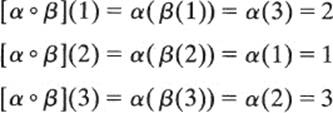
Thus

Note that in α ∘ β, β is applied first and α next. A graphic way of representing this is

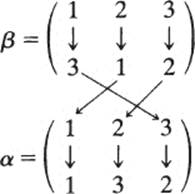
The other combinations of elements of S₃ may be computed in the same fashion. The student should check the following table, which is the table of the group S₃:

By a group of permutations we mean any group S_A or S_n, or any subgroup of one of these groups. Among the most interesting groups of permutations are the groups of symmetries of geometric figures. We will see how such groups arise by considering the group of symmetries of the square.

We may think of a symmetry of the square as any way of moving a square to make it coincide with its former position. Every time we do this, vertices will coincide with vertices, so a symmetry is completely described by its effect on the vertices.

Let us number the vertices as in the following diagram:

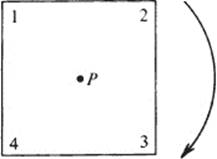
The most obvious symmetries are obtained by rotating the square clockwise about its center P, through angles of 90°, 180°, and 270°, respectively. We indicate each symmetry as a permutation of the vertices; thus a clockwise rotation of 90° yields the symmetry

for this rotation carries vertex 1 to 2,2 to 3, 3 to 4, and 4 to 1. Rotations of 180° and 270° yield the following symmetries, respectively:

The remaining symmetries are flips of the square about its axes A, B, C, and D:

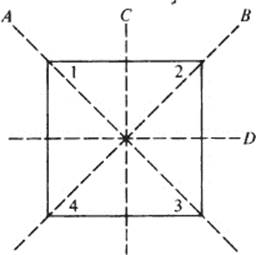
For example, when we flip the square about the axis A, vertices 1 and 3 stay put, but 2 and 4 change places; so we get the symmetry

In the same way, the other flips are

and

One last symmetry is the identity

which leaves the square as it was.

The operation on symmetries is composition: R_i ∘ R_j is the result of first performing R_j, and then R_i. For example, R₁ ∘ R₄ is the result of first flipping the square about its axis A, then rotating it clockwise 90°:

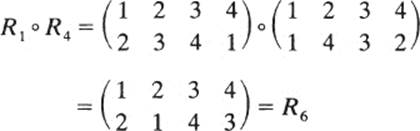
Thus, the net effect is the same as if the square had been flipped about its axis C.

The eight symmetries of the square form a group under the operation ∘ of composition, called the group of symmetries of the square.

For every positive integer n ≥ 3, the regular polygon with n sides has a group of symmetries, symbolized by D_n, which may be found as we did here. These groups are called the dihedral groups. For example, the group of the square is D₄, the group of the pentagon is D₅, and so on.

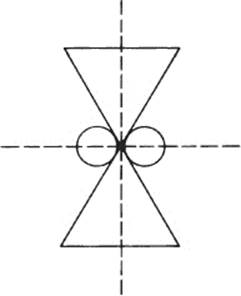
Every plane figure which exhibits regularities has a group of symmetries. For example, the following figure, has a group of symmetries consisting of two rotations (180° and 360°) and two flips about the indicated axes. Artificial as well as natural objects often have a surprising number of symmetries.

Far more complicated than the plane symmetries are the symmetries of objects in space. Modern-day crystallography and crystal physics, for example, rely very heavily on knowledge about groups of symmetries of three-dimensional shapes.

Groups of symmetry are widely employed also in the theory of electron structure and of molecular vibrations. In elementary particle physics, such groups have been used to predict the existence of certain elementary particles before they were found experimentally!

Symmetries and their groups arise everywhere in nature: in quantum physics, flower petals, cell division, the work habits of bees in the hive, snowflakes, music, and Romanesque cathedrals.

EXERCISES

A. Computing Elements of S₆

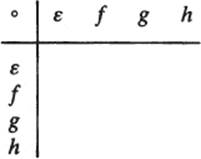
1 Consider the following permutations f, g, and h in S₆:

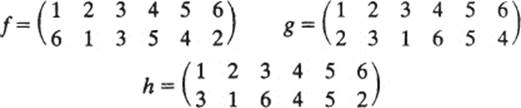
Compute the following:

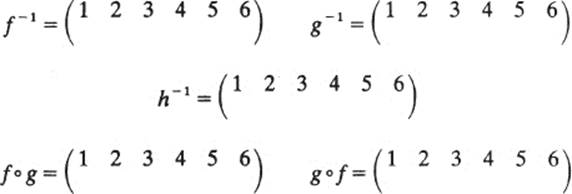
2 f °(g ∘ h) =

3 g ∘ h⁻¹ =

4 h ∘ g⁻¹° f⁻¹ =

5 g ∘ g ∘ g =

B. Examples of Groups of Permutations

1 Let G be the subset of S₄ consisting of the permutations

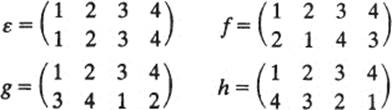
Show that G is a group of permutations, and write its table:

2 List the elements of the cyclic subgroup of S₆ generated by

3 Find a four-element abelian subgroup of S₅. Write its table.

4 The subgroup of S₅ generated by

has six elements. List them, then write the table of this group:

C. Groups of Permutations of

In each of the following, A is a subset of and G is a set of permutations of A. Show that G is a subgroup of S_A, and write the table of G.

1 A is the set of all x ∈ such that x ≠ 0,1. G = {ε, f, g}, where f(x) = 1 /(1 − x) and g(x) = (x − 1) /x.

2 A is the set of all the nonzero real numbers. G = {ε, f, g, h}, where f(x) = 1/x, g(x) = −x, and h(x) = –1/x.

3 A is the set of all the real numbers x ≠ 0, 1. G = {ε, f, g, h, k}, where f(x) = 1 − x, g(x) = 1/x, h(x) = 1/(1 − x), j(x) = (x − 1)/x, and k(x) = x/(x − 1).

4 A is the set of all the real numbers x ≠ 0,1,2. G is the subgroup of S_A generated by f(x) = 2 − x and g(x) = 2/x. (G has eight elements. List them, and write the table of G.)

† D. A Cyclic Group of Permutations

For each integer n, define f_n by f_n(x) = x + n.

1 Prove: For each integer n, f_n is a permutation of , that is, f_n ∈ S_R.

# 2 Prove that f_n ∘ f_m = f_{n + m} and .

3 Let G = {f_n : n ∈ }. Prove that G is a subgroup of S_R.

4 Prove that G is cyclic. (Indicate a generator of G.)

† E. A Subgroup of S

For any pair of real numbers a ≠ 0 and b, define a function f_a,b as follows:

f_a,b (x) = ax + b

1 Prove that f_{a, b} is a permutation of , that is, f_a,b ∈ S.

2 Prove that f_a,b ∘ f_c,d = f_{ac, ad + b}.

# 3 Prove that .

4 Let G = {f_a,b : a ∈ , b ∈ , a ≠ 0}. Show that G is a subgroup of S_R.

F. Symmetries of Geometric Figures

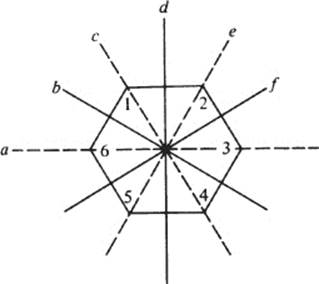
1 Let G be the group of symmetries of the regular hexagon. List the elements of G (there are 12 of them), then write the table of G.

2 Let G be the group of symmetries of the rectangle. List the elements of G (there are four of them), and write the table of G.

3 List the symmetries of the letter Z and give the table of this group of symmetries. Do the same for the letters V and H.

4 List the symmetries of the following shape, and give the table of their group.

(Assume that the three arms are of equal length, and the three central angles are equal.)

G. Symmetries of Polynomials

Consider the polynomial p = (x₁ − x₂)² + (x₃ − x₄)². It is unaltered when the subscripts undergo any of the following permutations:

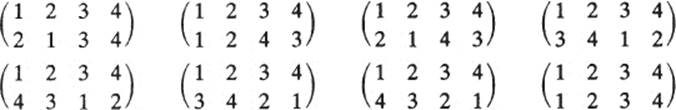
For example, the first of these permutations replaces p by

(x₂ − x₁)² + (x₃ − x₄)²

the second permutation replaces p by (x₁ − x₂)² + (x₄ − x₃)²; and so on. The symmetries of a polynomial ρ are all the permutations of the subscripts which leave ρ unchanged. They form a group of permutations.

List the symmetries of each of the following polynomials, and write their group table.

1p = x₁x₂ + x₂x₃

2p = (x₁ − x₂)(x₂ − x₃)(x₁ − x₃)

3p = x₁x₂ + x₂x₃ + x₁x₃

4p = (x₁ − x₂)(x₃ − x₄)

H. Properties of Permutations of a Set A

1 Let A be a set and a ∈ A. Let G be the subset of S_A consisting of all the permutations f of A such that f(a) = a. Prove that G is a subgroup of S_A.

# 2 If f is a permutation of A and a ∈ A, we say that f moves a if f (a) ≠ a. Let A be an infinite set, and let G be the subset of S_A which consists of all the permutations f of A which move only α finite number of elements of A. Prove that G is a subgroup of S_A.

3 Let A be a finite set, and B a subset of A. Let G be the subset of S_A consisting of all the permutations f of A such that f(x) ∈ B for every x ∈ B. Prove that G is a subgroup of S_A.

4 Give an example to show that the conclusion of part 3 is not necessarily true if A is an infinite set.

I. Algebra of Kinship Structures (Anthropology)

Anthropologists have used groups of permutations to describe kinship systems in primitive societies. The algebraic model for kinship structures described here is adapted from An Anatomy of Kinship by H. C. White. The model is based on the following assumptions, which are widely supported by anthropological research:

(i)The entire population of the society is divided into clans. Every person belongs tö one, and only one, clan. Let us call the clans k₁, k₂,..., k_n.

(ii)In every clan k_i, all the men must choose their wives from among the women of a specified clan k_j. We symbolize this by writing w(k_i) = k_j.

(iii)Men from two different clans cannot marry women from the same clan. That is, if k_i ≠ k_j, then w(k_i) ≠ w(k_j).

(iv)All the children of a couple are assigned to some fixed clan. So if a man belongs to clan k_i, all his children belong to a clan which we symbolize by c(k_i).

(v)Children whose fathers belong to different clans must themselves be in different clans. That is, if k_i ≠ k_j, then c(k_i) ≠ c(k_j).

(vi)A man cannot marry a woman of his own clan. That is, w(k_i) ≠ k_i.

Now let K = {k₁,k₂,. . ., k_n} be the set of all the distinct clans. By (ii), w is a function from K to K, and by (iv), c is a function from K to K. By (iii), w is an injective function; hence (see Exercise F2 of Chapter 6) w is a permutation of K. Likewise, by (v), c is a permutation of K.

Let G be the group of permutations generated by c and w; that is, G consists of c, w, c⁻¹, w⁻¹, and all possible composites which can be formed from these —for example, c ∘ w ∘ w ∘ c⁻¹ ∘ w⁻¹. Clearly the identity function ε is in G since, for example, ε = c ∘ c⁻¹. Here are two final assumptions:

(vii)Every person, in any clan, has a relation in every other clan. This means that for any k_i and k_j in K, there is a permutation α in G such that α(k_i) = k_j

(viii)Rules of kinship apply uniformly to all clans. Thus, for any α and β in G, if α(k_j) = β(k_j) for some specific clan k_j, it necessarily follows that α(k_i) = β(k_i) for every clan k_i

Prove parts 1–3:

1 Let α ∈ G. If α(k_i) = k_i for any given k_i, then α = ε.

2 Let a α G. There is a positive integer m ≤ n such that α^m = ε.

[α^m = α ∘ α ∘ ··· ∘ α (m factors of α). HINT: Consider α(k₁), α²(k₁), etc.]

3 The group G consists of exactly n permutations.

Explain parts 4–9.

4 If a person belongs to clan k_i, that person’s father belongs to clan c⁻¹(k_i). If a woman belongs to clan k_j, her husband belongs to clan w⁻¹(k_j).

5 If any man is in the same clan as his son, then c = ε. If any woman is in the same clan as her son, then c = w.

6 If a person belongs to clan k_i, the son of his mother’s sister belongs to clan c ∘ w⁻¹ ∘ w ∘ c⁻¹(k_i). Conclude that marriage between matrilateral parallel cousins (marriage between a woman and the son of her mother’s sister) is prohibited.

7 Marriage between a man and the daughter of his father’s sister is prohibited.

8 If matrilateral cross-cousins may marry (that is, a woman may marry the son of her mother’s brother), then c ∘ w = w⁻¹ ∘ c.

9 If patrilateral cross-cousins may marry (a woman may marry the son of her father’s sister), then c and w⁻¹ commute.