ACT Math For Dummies (2011)

Part III. Digging In to Intermediate Algebra and Coordinate Geometry

Chapter 9. Practice Problems for Intermediate Algebra and Coordinate Geometry

Ready for some practice questions on intermediate algebra and coordinate geometry from the material in Chapters 7 and 8? Sure you are! This chapter provides you with plenty of practice as well as detailed explanations of how to arrive at the correct answers. If you find you’re struggling with any particular concepts, refer to Chapter 7 or 8 again for some more review.

Intermediate Algebra and Coordinate Geometry Practice Problems

Here are 30 questions that cover what you need to know about inequalities, systems of equations, graphing, functions, and much more. When you’re finished with the questions, check your answers later in the chapter.

1. Which of the following is equivalent to the inequality –5(3x – 2) < 25 – 12x?

(A) x > 5

(B) x < 5

(C) x > –5

(D) x < –5

(E) x ≤ 5

2. In the following figure, which line segment has a slope of ?

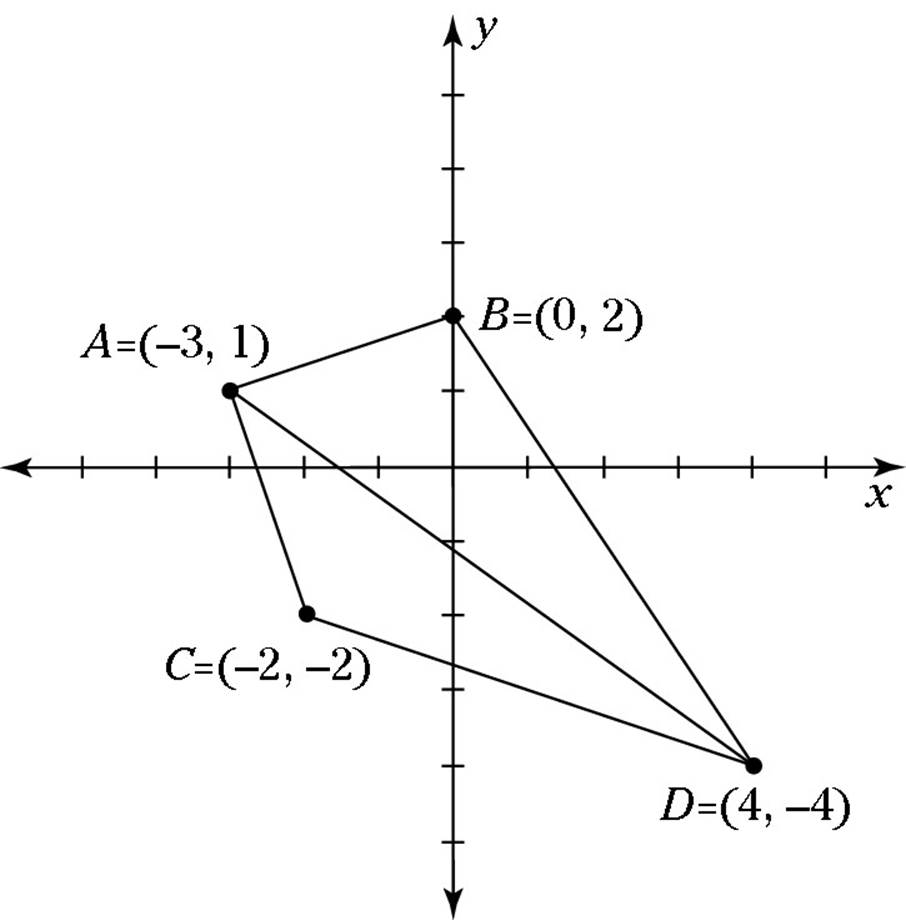
(F)

(G)

(H)

(J)

(K)

3. Anne and Bette are both celebrating their birthdays today. If Anne were ten years older and Bette were three years younger, then Anne would be twice as old as Bette. And if Anne were three years older and Bette were twice her current age, Anne’s age would be that of Bette. How old is Bette?

(A) 26

(B) 28

(C) 32

(D) 35

(E) 36

4. If a and b are the two values that satisfy the equation x² – 9x + 20 = 0, what is the value of a² + b²?

(F) 25

(G) 41

(H) 100

(J) 104

(K) 401

5. What is the formula of a line that is perpendicular to y = 5x + 11 and includes the point (0, 9)?

(A) y = 5x + 9

(B)

(C)

(D)

(E)

6. If f(x) = 8x² and g(x) = 2x – 3, what is the value of ?

(F) –1

(G) –9

(H) –15

(J) –19

(K) –21

7. In the following figure, what would be the midpoint of ?

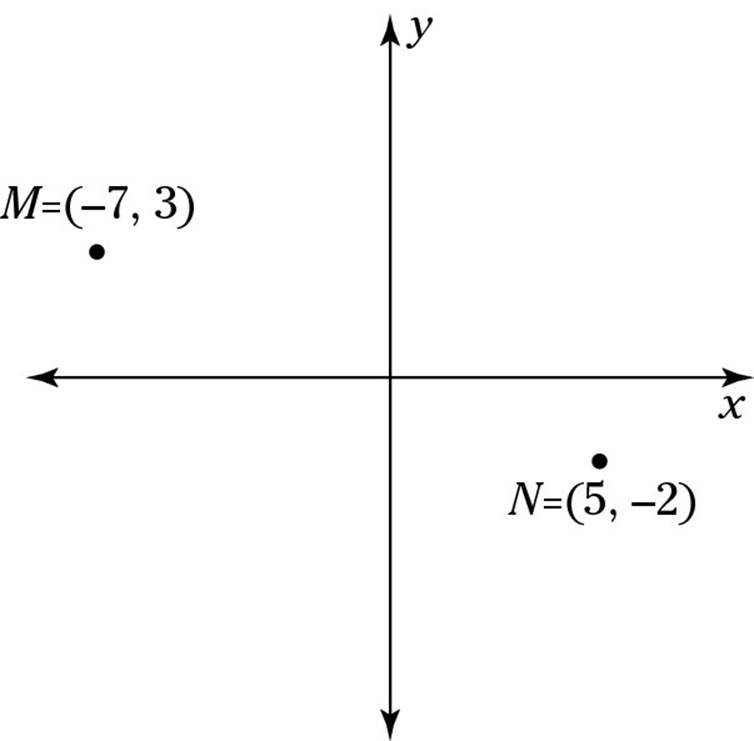
(A)

(B)

(C)

(D)

(E)

8. In the following figure, if g(x) is the reflection across the x-axis of f(x) = 2x² + 1, then g(x) =

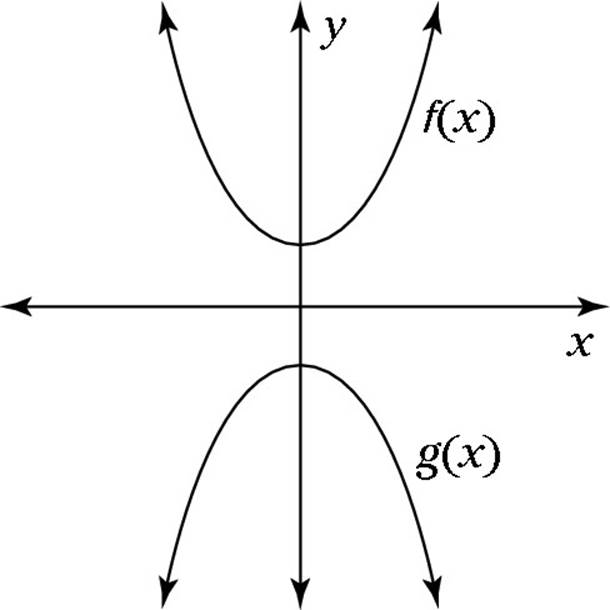
(F) 2x² + 1

(G) 2x² – 1

(H) –2x² + 1

(J) –2x² – 1

(K) 2(–x)² + 1

9. What is the slope of a line that includes the point (3, 2) and crosses the x-axis at x = 9?

(A) 3

(B) –3

(C)

(D)

(E) Cannot be determined from the information given.

10. If 3x² + 12x + 4 = 0, which of the following is a possible value of x?

(F)

(G)

(H)

(J)

(K)

11. What is the formula of a line with a slope of –2 that includes the point (7, 1)?

(A) y = –2x – 13

(B) y = –2x + 15

(C)

(D)

(E)

12. Two values a and b are inversely proportional such that if a = 3, then b = 10. Which of the following is true?

(F) If a = 1, then

(G) If a = 5, then b = 6

(H) If a = 6, then b = 20

(J) If a = 6.5, then b = 6.5

(K) If a = 30, then b = 0

13. In the following figure, what is the length of ?

(A)

(B)

(C)

(D)

(E)

14. Which of the following could be the graph of the equation y = 3x² – 10x – 2?

(F)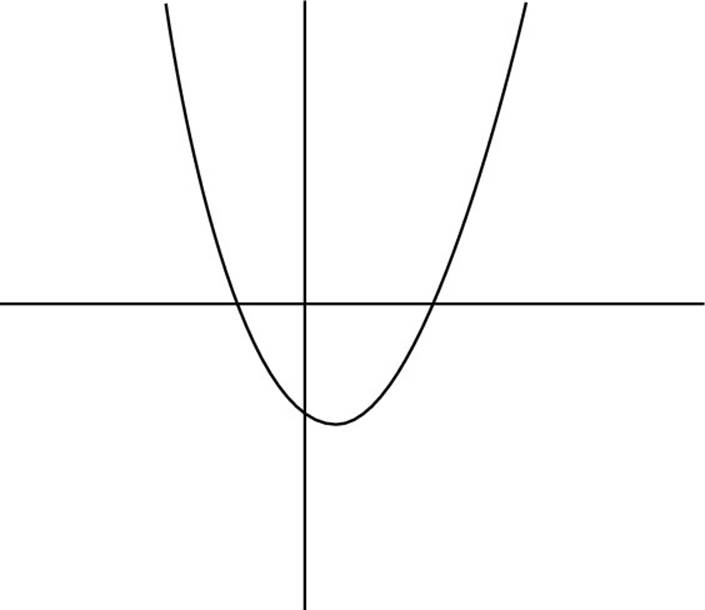

(G)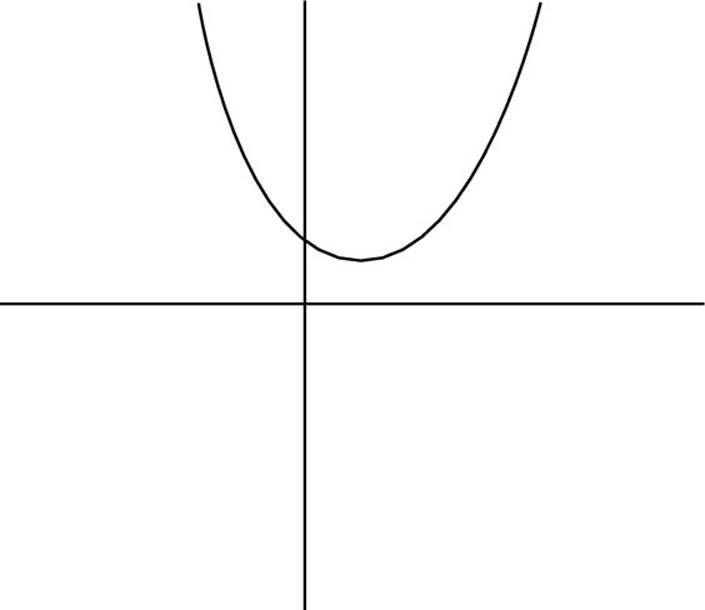

(H)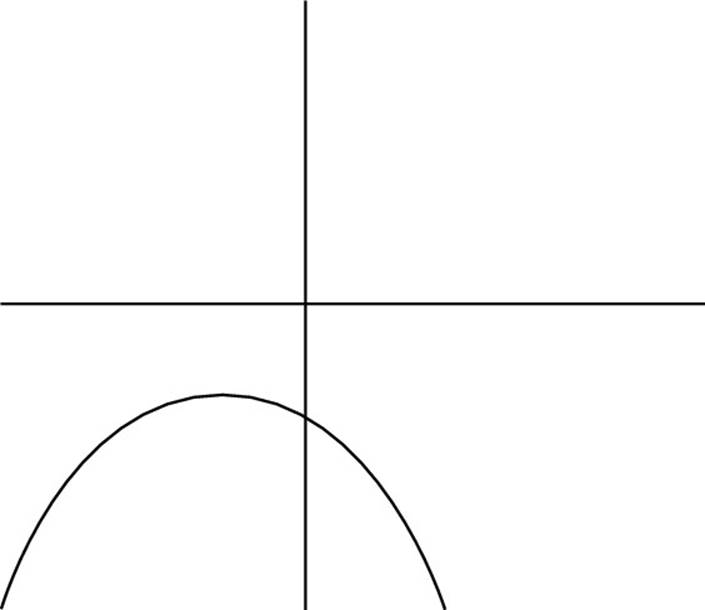

(J)

(K)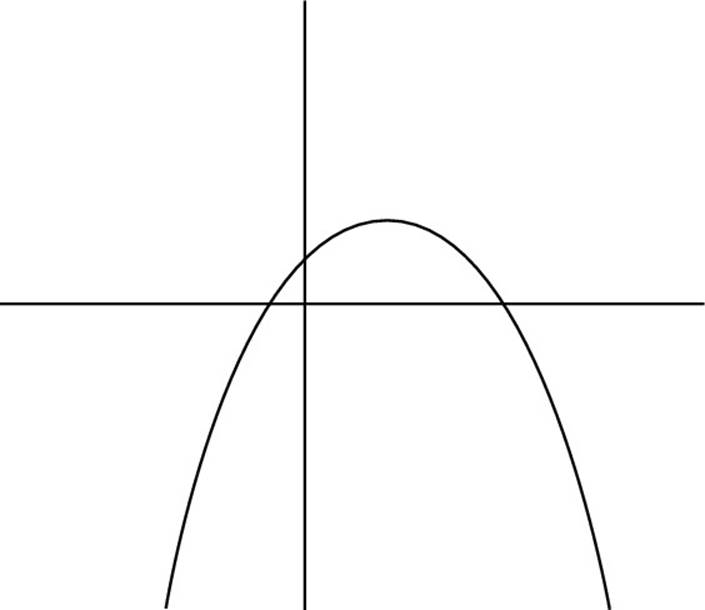

15. Which of the following is the solution set for n for the inequality |5 – 2n| > 9?

(A) 2 < n < 7

(B) –2 < n < 7

(C) –7 < n < 2

(D) n < –2 or n > 7

(E) n < –7 or n > 2

16. Which of the following transformations shifts y = x² + 2x + 3 horizontally one unit to the right?

(F) y = x² + 2

(G) y = x² + 3

(H) y = x² + 2x + 2

(J) y = x² + 2x + 4

(K) y = x² + 4x + 6

Questions 17 and 18 are based on the following information: The Kleen-Pro Housecleaning Company charges a flat rate of $150 for an initial visit of four hours and $20 per hour for each subsequent visit.

17. Which of the following functions outputs the dollar cost of x hours of service by Kleen-Pro for any value of x ≥ 4?

(A) f(x) = 20x + 70

(B) f(x) = 20x – 70

(C) f(x) = 20x + 150

(D) f(x) = 20x – 150

(E) f(x) = 20x + 220

18. What is the cost of 20 hours of Kleen-Pro service?

(F) $250

(G) $300

(H) $400

(J) $470

(K) $550

19. If g(x) shifts the function f(x) three units down and six units to the left, then g(x) =

(A) f(x + 3) – 6

(B) f(x – 3) + 6

(C) f(x – 3) – 6

(D) f(x + 6) – 3

(E) f(x – 6) – 3

20. Which of the following are the coordinates of the vertex for the parabola whose equation is y = x² + 6x + 5?

(F) (3, 4)

(G) (–3, 4)

(H) (–3, –4)

(J) (4, –3)

(K) (–4, –3)

21. Which of the following values of x does NOT satisfy the inequality 2x² – x – 10 < 0?

(A)

(B)

(C)

(D)

(E)

22. On an xy-graph, line r and line s are perpendicular to each other, line r intersects (0, 11), and the equation of line s is y = 3x + 1. At what point do line r and line s intersect?

(F) (3, 8)

(G) (3, 9)

(H) (3, 10)

(J) (4, 9)

(K) (4, 10)

23. If 3p + 4q = –14 and 7p + 5q = 15, what is the value of p + q?

(A) –1

(B) –2

(C) –3

(D) –4

(E) –5

24. If Equation 1 is y = x + 1 and Equation 2 is y = x³, which of the following is true?

(F) Equation 1 is quadratic.

(G) Equation 1 is cubic.

(H) Equation 2 is linear.

(J) Equation 2 is quadratic.

(K) Equation 2 is cubic.

25. Which of the following values is in the domain of the function ?

(A) 1

(B) 2

(C) 3

(D) 4

(E) 5

26. In the following figure, the equation for the parabola is y = x² + 1. The line crosses the origin and is tangent to the parabola at x = 1. What is the equation of the line?

(F) y = x

(G) y = 2x

(H) y = 2x + 1

(J)

(K)

27. In the following figure, the circle is centered at K and includes the origin. Which of the following is the formula for this circle?

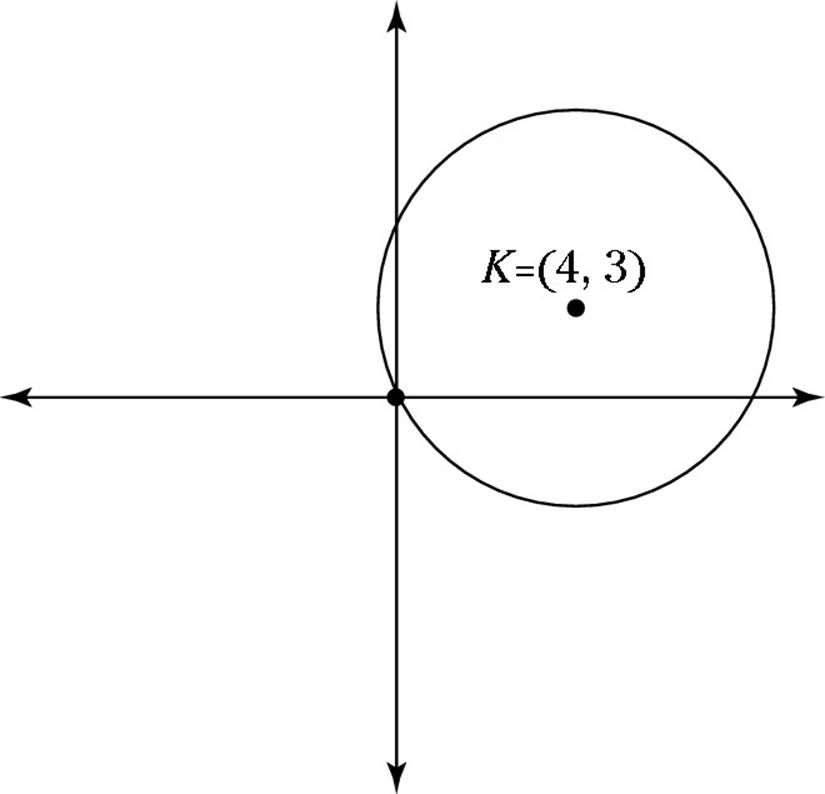
(A) (x + 4)² + (y + 3)² = 5

(B) (x – 4)² – (y – 3)² = 5

(C) (x + 4)² + (y + 3)² = 25

(D) (x – 4)² + (y – 3)² = 25

(E) (x + 4)² – (y + 3)² = 25

28. What is the range of f(t) = (t² + 1)² – 1?

(F) f(t) ≥ 0

(G) f(t) ≥ 1

(H) f(t) ≥ –1

(J) f(t) ≥ 2

(K) f(t) ≥ –2

29. Which of the following graphs is a function but not a polynomial?

(A)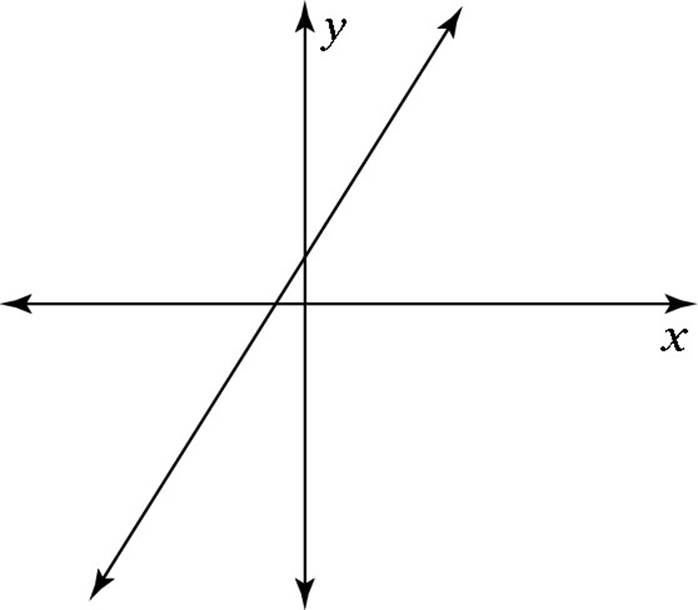

(B)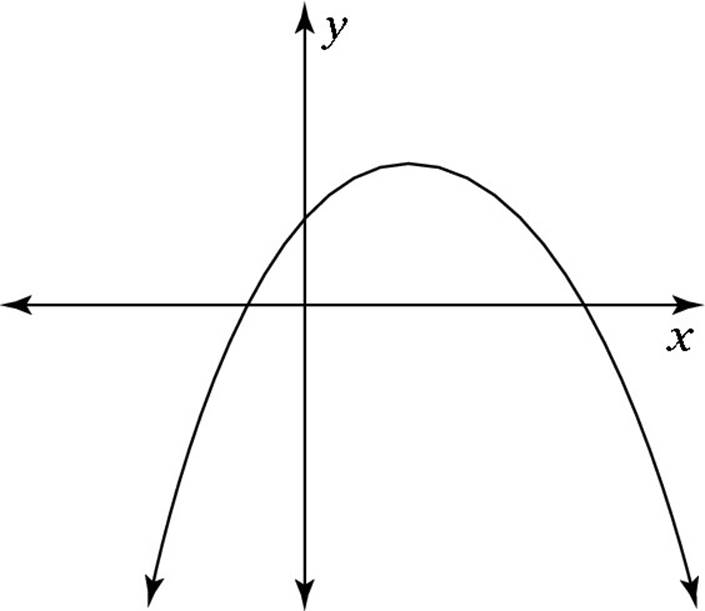

(C)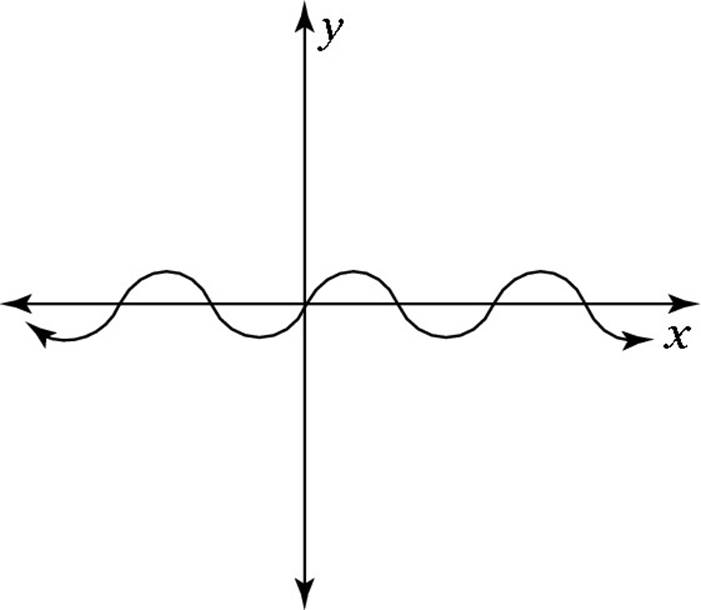

(D)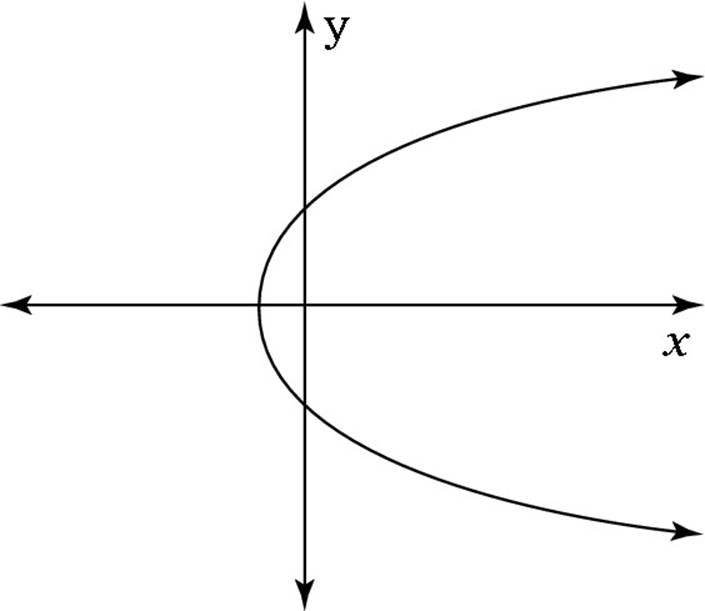

(E)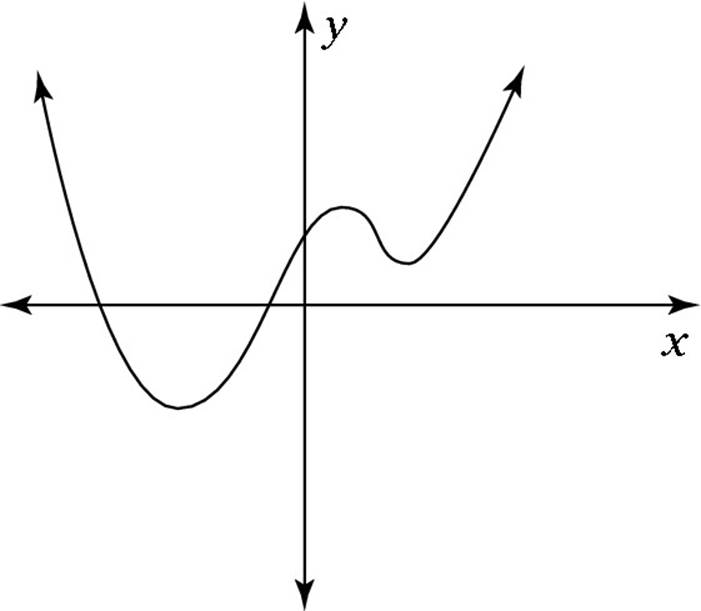

30. Pam, Rhoda, and Tanya all work as servers at a local restaurant. This week, Pam and Rhoda together worked 3 times as many hours as Tanya. Pam and Tanya together worked 1.5 times as many hours as Rhoda. Rhoda and Tanya together worked 36 hours more than Pam. What is the sum of their hours?

(F) 96

(G) 108

(H) 120

(J) 132

(K) 144

Solutions to Intermediate Algebra and Coordinate Geometry Practice Problems

In this section, you find the answers to the 30 practice questions from the preceding section. We include the answers as well as the worked-out solutions.

1. C. First, notice that the inequality (<) is exclusive, so any equivalent inequality is also exclusive; therefore, you can rule out Choice (E). Simplify the inequality by distributing and combining like terms:

–5(3x – 2) < 25 – 12x

–15x + 10 < 25 – 12x

–3x + 10 < 25

–3x < 15

Divide both sides by –3 and reverse the inequality:

x > –5

2. K. A negative slope slants down as the line goes from left to right, so you can rule out Choice (F). Use the rise-run slope formula for each of the remaining line segments:

3. A. Let a be Anne’s age and b be Bette’s age. If Anne were ten years older (a + 10) and Bette were three years younger (b – 3), then Anne would be twice as old as Bette, so:

a + 10 = 2(b – 3)

a + 10 = 2b – 6

a = 2b – 16

If Anne were three years older (a + 3) and Bette were twice her current age (2b), Anne’s age would be that of Bette, so:

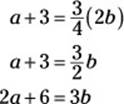
Substitute 2b – 16 for a into the last equation:

2(2b – 16) + 6 = 3b

4b – 32 + 6 = 3b

4b – 26 = 3b

–26 = –b

26 = b

4. G. Begin to solve this equation by factoring:

x² – 9x + 20 = 0

(x )(x ) = 0

List all of the combinations (including negatives) that multiply to 20:

1 × 20 2 × 10 4 × 5

–1 × –20 –2 × –10 –4 × –5

To factor, use the combination whose sum is –9; that is, use –4 + (–5) = –9:

(x – 4)(x – 5) = 0

Next, break the equation into two separate equations and solve:

x – 4 = 0 x – 5 = 0

x = 4 x = 5

Thus, the values of a and b are 4 and 5, so

a² + b² = 4² + 5² = 16 + 25 = 41

5. D. A line that’s perpendicular to y = 5x + 11 has a slope that’s the negative reciprocal of 5, so its slope is . The line also includes the point (0, 9), which is the y-intercept, so b = 9. Plug these values into the slope-intercept formula to get your answer:

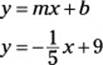
6. H. Begin by substituting values into the functions:

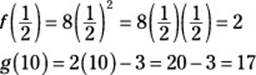
Now substitute:

7. B. M = (–7, 3) and N = (5, –2). So, to find your answer, plug these four values into the midpoint formula:

8. J. The function g(x) is a reflection of f(x) = 2x² + 1 vertically across the x-axis, so g(x) equals the negation of f(x):

g(x) = –(2x² + 1) = –2x² – 1

9. D. The line that includes the point (3, 2) and crosses the x-axis at x = 9 also includes the point (9, 0). Plug these values into the two-point formula for slope:

10. H. The equation 3x² + 12x + 4 = 0 can’t be solved by factoring, so use the quadratic formula:

Now simplify:

This answer provides two possible solutions, so the correct answer is Choice (H).

11. B. The line has a slope of –2, so m = –2. You need to find the y-intercept, so plug in x = 7 and y = 1 into the slope-intercept form and solve for b:

y = mx + b

1 = –2(7) + b

1 = –14 + b

15 = b

Now plug b = 15 and m = –2 back into the slope-intercept form:

y = –2x + 15

12. G. When two values are inversely proportional, their product equals a constant k. If a = 3, then b = 10, so ab = 30. Thus, if a = 5, then b = 6 (because 5 × 6 = 30). As a result, the correct answer is Choice (G).

13. D. U = (–1, –8) and V = (3, 2). To find your answer, simply plug these values into the distance formula:

Now simplify:

14. F. In the equation y = 3x² – 10x – 2, a = 3, b = –10, and c = –2. The coefficient a is positive, so the graph is concave up, which rules out Choices (H) and (K). The coefficients a and b have different signs, which shifts the graph to the right, so Choice (J) also is ruled out. And the coefficient c is negative, which rules out Choice (G). So the only answer left is Choice (F).

15. D. To drop the absolute value bars, split the inequality |5 – 2n| > 9 into two separate inequalities as follows:

5 – 2n > 9 5 – 2n < –9

Solve both equations for n:

5 – 2n > 9 5 – 2n < –9

–2n > 4 –2n < –14

n < –2 n > 7

16. F. To shift y = x² + 2x + 3 horizontally one unit to the right, change each x to x – 1 and simplify:

y = (x – 1)² + 2(x – 1) + 3

y = (x – 1)(x – 1) + 2(x – 1) + 3

y = x² – 2x + 1 + 2x – 2 + 3

y = x² + 2

17. A. The first 4 hours of service cost $150, and each subsequent hour costs $20. Thus, when counting hours, you need to subtract 4 hours before multiplying this count by 20, and then you add in $150. Here’s what the initial function will look like:

f(x) = 20(x – 4) + 150

Then you simplify it like this:

f(x) = 20x – 80 + 150

f(x) = 20x + 70

18. J. Plug 20 for x into the function f(x) = 20x + 70, which you found in the previous problem:

f(20) = 20(20) + 70 = 400 + 70 = 470

19. D. To shift the function f(x) units down, subtract 3 from the entire function f(x), which changes it to f(x) – 3. To shift it 6 units to the left, change x to x + 6, which changes the function to f(x + 6) – 3. That’s it. The correct answer is Choice (D).

20. H. In the equation y = x² + 6x + 5, a = 1, b = 6, and c = 5. Plug these numbers into the formula for the vertex (if you don’t remember this formula, you can draw a graph or use your calculator to draw one):

Next, simplify:

21. A. Begin by treating the quadratic inequality as a quadratic equation:

2x² – x – 10 = 0

Next factor the equation:

(2x – 5)(x + 2) = 0

Now split it into two separate equations and solve for x:

 x + 2 = 0

 x = –2

The parabola for this function is concave up because the x² term is positive and crosses the x-axis at and –2. Because the function produces negative values between these two values of x, the inequality is satisfied between these two values. Thus, the inequality isn’t satisfied when x is , making the correct answer Choice (A).

22. H. To answer the question, you first need to find the equation of line r. It’s perpendicular to line s, whose slope is 3, so the slope of line r is . It intersects (0, 11), so the y-intercept of line r is b = 11. Plug these values into the slope-intercept form to get the equation for line r:

The equations for line r and line s form a system of equations. Set the right sides of both equations equal to each other and then solve for x:

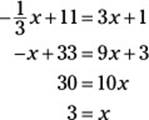
Now substitute 3 for x into either equation. The easier one is the equation for line s, so try that one:

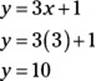
Thus, x = 3 and y = 10. So the correct answer is (3, 10).

23. A. This system of equations solves more easily by combining equations. Multiply the first equation by 5 and the second equation by 4:

3p + 4q = –14 becomes  15p + 20q = –70

7p + 5q = 15 becomes  28p + 20q = 60

Now subtract the second equation from the first:

15p + 20q = –70

– 28p + 20q = 60

–13p = –130

Solve for p:

p = 10

Finally, substitute 10 for p in one of the equations. The first equation looks easier, so go for that one:

3p + 4q = –14

3(10) + 4q = –14

30 + 4q = –14

4q = –44

q = –11

Thus, p + q = 10 + (–11) = –1, so the correct answer is Choice (A).

24. K. Equation 1 is a first-degree equation, so it’s linear. Equation 2 is a third-degree equation, so it’s cubic. Thus, the correct answer is Choice (K).

25. B. The denominator can’t equal 0. So you know that x isn’t 1, because then 1 – x = 1 – 1 = 0. Thus, Choice (A) is wrong. The value inside the square root also can’t be a negative number, so:

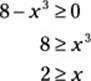
As a result, x must be less than or equal to 2, so x can’t equal 3, 4, or 5, which rules out Choices (C), (D), and (E). The correct answer has to be Choice (B).

26. G. The line is tangent to the parabola, so they share exactly one point. The x value of this point is 1, so plug it into the equation of the parabola and solve for y:

y = x² + 1 = 1² + 1 = 2

So the coordinates of this point is (1, 2). The line includes this point and the origin (0, 0), so use the rise-run slope formula:

Thus, the slope of the line is m = 2 and its y-intercept is b = 0. Plug these values into the slope-intercept form to get your answer:

y = mx + b

y = 2x + 0

y = 2x

27. D. The formula for a circle centered at (h, k) with radius r is

(x – h)² + (y – k)² = r²

The circle is centered at (4, 3), so

(x – 4)² + (y – 3)² = r²

Thus, you can rule out Choices (A), (C), and (E). The radius is the distance from (4, 3) to any point on the circle, which includes (0, 0), so use the distance formula to calculate the radius:

Now simplify:

The radius is r = 5, so the formula is as follows:

(x – 4)² + (y – 3)² = 5²

(x – 4)² + (y – 3)² = 25

28. F. Start from the inside of the function f(t) = (t² + 1)² – 1 and work your way out: The value of t² can’t be negative, so its lowest value is 0; therefore, the range of f(t) = t² is f(t) ≥ 0. So when you add 1 to this function, its lowest value becomes 1; therefore, the range of f(t) = t² + 1 is f(t) ≥ 1. When you square this function, its lowest value remains 1; therefore, the range of f(t) = (t² + 1)² is f(t) ≥ 1. Finally, when you subtract 1 from this function, its lowest value becomes 0; therefore, the range of f(t) =(t² + 1)² – 1 is f(t) ≥ 0. To test this, notice that when t = 0, f(t) = 0, but at all other values of t, f(t) > 0.

29. C. Choice (D) isn’t a function, because at least one x-value has more than one y-value (that is, a vertical line can pass through it twice). So you can rule that choice out. Choices (A), (B), and (E) are all polynomials — linear, quadratic, and fourth-degree, respectively — so you can rule them out as well. The correct answer is Choice (C), which is a function but not a polynomial.

30. H. Let p, r, and t, respectively, be the number of hours that Pam, Rhoda, and Tanya worked. With those variables you can make these three equations:

p + r = 3t

p + t = 1.5r

r + t = p + 36

Subtract r from both sides of the first equation:

p = 3t – r

Now substitute 3t – r for p into the second and third equations:

3t – r + t = 1.5r

r + t = 3t – r + 36

Combine like terms in these two equations:

4t = 2.5r

2r = 2t + 36

You can further simplify these by multiplying the first equation by 2 and dividing the second equation by 2:

8t = 5r

r = t + 18

Substitute t + 18 for r in the first equation and solve for t:

8t = 5(t + 18)

8t = 5t + 90

3t = 90

t = 30

Substitute 30 for t back into one of the two previous equations (r = t + 18 looks easiest) and solve for r:

r = 30 + 18

r = 48

Finally, substitute 30 for t and 48 for r into any of the original equations (p + r = 3t looks easiest) and solve for p:

p + 48 = 3(30)

p + 48 = 90

p = 42

Thus, the sum of their hours is p + r + t = 42 + 48 + 30 = 120, making Choice (H) the correct answer.