ACT Math For Dummies (2011)
Part V. Tracking Your Progress with Practice Tests
Chapter 14. Practice Test 1: Answers and Explanations
Congratulations! You’ve completed Practice Test 1! You’re now ready to check your answers to see how you fared. In this chapter, I provide the answers, including detailed explanations and a bare-bones answer key. The answer key is great for when you’re checking your answers in a hurry, but I suggest that you review the detailed explanations for each question — even those you answered correctly. You’ll be surprised at how many tips and tricks you find throughout these explanations. Good luck!
Mathematics Test
1. D. The numbers increase at a somewhat steady rate, so you have to figure out how much you have to add to each number to produce the next in the sequence: 3 + 5 = 8; 8 + 6 = 14; 14 + 7 = 21; 21 + 8 = 29, and so on. The rule for the sequence is to add successively larger numbers to each number; therefore, the next number is 29 + 9 = 38.
2. H. Six hours equals 360 minutes, so Beth paints 5 rooms in 360 minutes. She paints 1 room in 360 ÷ 5 = 72 minutes, which equals 1 hour and 12 minutes.
3. D. Solve for x:
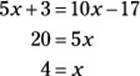
4. F. The greatest of the five possible answers is 20, so k is less than 20. Use trial and error to find the value of k:
Factors of 5: 1 5
Factors of 6: 1 2 3 6
Factors of 7: 1 7
Factors of 8: 1 2 4 8
Factors of 9: 1 3 9
Thus, k = 9, and the sum of the factors of k is 1 + 3 + 9 = 13.
5. E. William earned $3,200 × 10 = $32,000 as a teacher, and he earned $2,000 × 2 = $4,000 as a barista. So he earned $32,000 + $4,000 = $36,000 over the 12 months. Plug these values into the formula for the mean:
6. F. Let x equal the number and then change the words into an equation and solve for x:
4x – 7 = 11(x – 7)
4x – 7 = 11x – 77
70 = 7x
10 = x
7. B. The number line includes all values that are both greater than or equal –5, but strictly less than 5, so the correct answer is Choice (B).
8. J. The small triangle has a side with the length of 3, and the large triangle has a corresponding side with the length of 6, which is twice as long. The triangles are similar, so each side of the large triangle is twice the length of the corresponding side of the small triangle. One side of the small triangle has a length of 2, so the corresponding side of the large triangle is 4; thus, x = 4. One side of the small triangle has a length of 4, so the corresponding side of the large triangle is 8; thus, y = 8. Therefore, y = x + 4.
9. B. If n = 11, then:
(n – 3)2 = (11 – 3)2 = 82 = 64
Substitute 11 for n into each answer until you find one that equals 64:
(n + 6)(n – 6) = (17)(5) = 85 Wrong!
(n + 5)(n – 7) = (16)(4) = 64 You’ve found a match!
10. J. The area of the field is 22,500 square feet, so plug this value into the formula for the area of a square to find the length of the side:
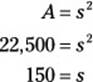
So the side of the field measures 150 feet. The diagonal of a square is the hypotenuse of a 45-45-90 triangle, which has three sides in a ratio of 
. Thus, the length of this diagonal is 
. (You can also use the Pythagorean theorem to find this result.)
11. C. Plug the values for the coordinates into the formula for the slope of a line:
12. H. To begin, find the area of each of the two sections by multiplying the lengths of the sides:
30 feet × 40 feet = 1,200 square feet
60 feet × 80 feet = 4,800 square feet
The total area that needs sod has an area of 1,200 + 4,800 = 6,000 square feet. Each individual square is 2 feet by 2 feet, so each has an area of 4 square feet. Because all the numbers are even, there will be no waste when the squares of sod are placed. Therefore, you just have to find the number of squares needed by dividing:
6,000 ÷ 4 = 1,500
13. C. The secant of an angle equals the hypotenuse over the adjacent angle, so
14. H. Solve the equation pq – 3r = 2 in terms of p and r by isolating the q on one side of the equal sign as follows:
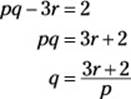
15. C. The problem states that f(x) = 4x2 – 5x – 5, so
f(–5) = 4(–5)2 – 5(–5) – 5 = 100 + 25 – 5 = 120
You also know that g(x) = 2x – 4, so
g(6) = 26 – 4 = 64 – 4 = 60
Therefore:
16. J. Let the two integers equal x and y, and then create the following equation and simplify:
xy + 4 = 40
xy = 36
So x and y are a pair of integers that equal 36. Try adding all possible combinations of two integers that multiply out to 36:
1 × 36 = 36 1 + 36 = 37
2 × 18 = 36 2 + 18 = 20
3 × 12 = 36 3 + 12 = 15
4 × 9 = 36 4 + 9 = 13
6 × 6 = 36 6 + 6 = 12
This list of sums includes 12, 13, 15, and 20, but not 18. Thus, no pair of integers both satisfies the original equation and adds up to 18.
17. B. ∠p and ∠r are opposite angles on the parallel lines, so they total 180°, which rules out Choice (A). The same is true of ∠q and ∠s, ruling out Choice (C). ∠t and ∠u are supplementary, so they add up to 180°, which rules out Choice (E). Finally, ∠r, ∠s, and ∠t are all vertical angles with the three interior angles of a triangle, so they total 180°, ruling out Choice (D). By elimination, the correct answer is Choice (B).
18. F. Factor the left side of the equation:
t2 – 6t + 8 = 0
(t – 2)(t – 4) = 0
Split this equation into two equations and solve:
t – 2 = 0 t – 4 = 0
t = 2 t = 4
Thus, a = 4 and b = 2. So a – b = 4 – 2 = 2.
19. D. The box has dimensions of 3 and 9 and a volume of 135, so plug these values into the formula for the volume of a box:
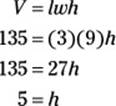
So the remaining dimension of the box is 5. The two longest dimensions are 5 and 9, so the area of the largest side is 5 × 9 = 45.
20. G. Solve the two equations, 3x + 2y = –2 and 5x – y = 14, as a system of equations. To do this, multiply the second equation by 2 and then add it to the first equation:
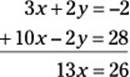
Now solve for x:
x = 2
Replace x with 2 in either equation and solve for y:
3(2) + 2y = –2
6 + 2y = –2
2y = –8
y = –4
At the point of intersection, x = 2 and y = –4, so this point is (2, –4).
21. B. The greatest common factor among the three terms in 12x2y3z4 – 30xy2 + 24x2y5z is 6xy2, so you can rule out Choices (C), (D), and (E). When you factor out 6xy2, the first term reduces to 2xyz4, so you also can rule out Choice (A).
22. K. The area of the square is 100, so each side of the square is 10 (because 102 = 100). The diameter of the circle is 10, so its radius is 5. Plug this value into the area formula for a circle:
The shaded region is half of this area, which is 
.
23. C. For m > 1,000 — that is, beyond 1,000 minutes of usage — the plan charges a usage fee based on the number of minutes used plus a flat rate of $50. With this information, you can create the following function:
f(m) = Usage fee + 50
The usage fee is $0.25 per minute; however, the first 1,000 minutes are already paid for. So the usage fee is 0.25(m – 1,000). Plug this value into the preceding function and simplify:
f(m) = 0.25(m – 1,000) + 50
f(m) = 0.25m – 250 + 50
f(m) = 0.25m – 200
24. J. First, plot the point (3, 4) on a graph. A slope of 2 means “up 2, over 1,” so plot this point on a graph, too. Here’s the resulting graph:
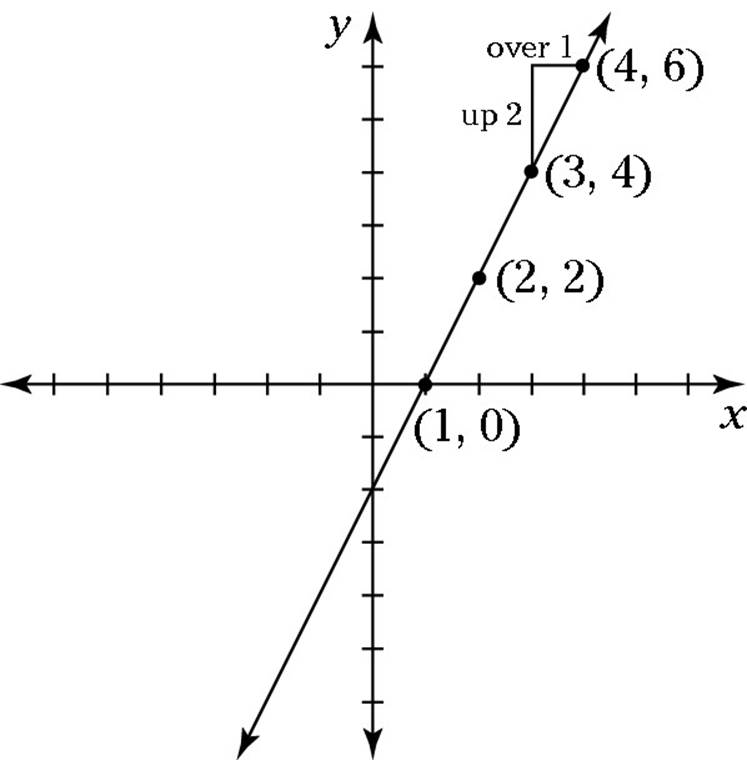
The line passes through the x-axis at 1, making the correct answer Choice (J).
25. D. Toni Morrison received 20% of the vote and John Steinbeck received 10%, so together they received 30%.
26. J. Cormac McCarthy received 15% of the vote, so use your calculator to find 15% of 260 = 39.
27. E. If Anne had $150 less, Katherine would have three times more than Anne. Make this statement into an equation and simplify:
3(a – 150) = k
3a – 450 = k
And if Katherine had twice as much, she would have three times more than Anne:
2k = 3a
Substitute 3a – 450 for k into the last equation and solve for a
2(3a – 450) = 3a
6a – 900 = 3a
–900 = –3a
300 = a
Now substitute 300 for a into the same equation and solve for k:
2k = 3(300)
2k = 900
k = 450
Thus, together Anne and Katherine have 300 + 450 = 750, so the right answer is Choice (E).
28. K. Split the inequality |2x + 7| > 11 into two inequalities: 2x + 7 > 11 and 2x + 7 < –11. Solve both for x:
2x + 7 > 11 2x + 7 < –11
2x > 4 2x < –18
x > 2 x < –9
Therefore, x < –9 or x > 2.
29. E. Plug the values into the distance formula:
Simplify:
30. F. To answer this question, you first have to solve for x. To do so, turn the log into an exponent:
log5 x = 2 means 52 = x
Thus, x = 25. The question asks for 
, so here’s your answer:
31. A. To begin, isolate the q and r terms in the first equation:
pq + 12 = 3p + pr
pq – pr + 12 = 3p
pq – pr = 3p – 12
Now factor out p on the left side of the equation:
p(q – r) = 3p – 12
Substitute 7 for q – r and solve for p:
7p = 3p – 12
4p = –12
p = –3
32. K. Anthony completed 30 push-ups the first day, 33 the second day, 36 the third day, and so on. Make a chart as follows:
1 2 3 4 5 . . . 10 . . . 15 . . . 20 . . . 25 . . . 30
30 33 36 39 42 57 72 87 102 117
To save time adding all these numbers, notice that the total of the first and 30th numbers is 30 + 117 = 147. This total is the same for the 2nd and 29th, the 3rd and 28th, and so on all the way to the 15th and 16th. Therefore, you have 15 pairings of days on which Anthony completed 147 pushups. You can simply multiply to find the total: 147 × 15 = 2,205.
33. D. A quadrilateral has four angles that add up to 360°, so make an equation as follows:
90 + 2x + x + x = 360
90 + 4x = 360
4x = 270
x = 67.5
34. H. Plug k into the formula for the volume of a cube and 10k into the formula for the volume of the surface area of a cube:
Substitute s3 for k in the second equation and solve for s:
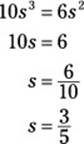
35. D. To begin, put the equation in terms of two powers with the same base. A good base to use is 2:
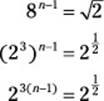
Because the bases are the same, the exponents are also the same. As a result, you can drop the bases and make an equation by setting the exponents equal to each other:
Now solve for n:
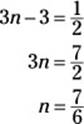
36. J. To answer this question, you simply use the midpoint formula:
37. C. To begin, simplify the problem to remove the fractions:
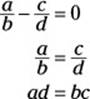
Now substitute 7 for bc:
ad = 7
Because ad equals a constant, a and d are inversely proportional.
38. G. Plug the radius of 10 into the formula for the circumference of a circle:
The area of the shaded region is 10% of the area of the circle, so the arc length from P to Q is 10% of the circumference of the circle. Therefore, the arc length is 2π.
39. B. To begin, FOIL the values in the parentheses:
(4 + 2i)(4 – 2i) = 16 – 8i + 8i – 4i2 = 16 – 4i2
Substitute –1 for i2:
= 16 – 4(–1) = 16 + 4 = 20
40. G. In this quadratic function of the form y = ax2 + bx + c, a = 175, b = –33, and c = –2,000. Because a is positive, the parabola is concave up, which rules out Choices (H) and (J). Because c is negative, the y intercept is below the origin, which rules out Choice (K). Because a and b have different signs, the graph shifts to the right, which rules out Choice (F). So, by elimination, you know that the correct answer is Choice (G).
41. D. The tip is a percent increase of 15%, which is 115%. Let x equal the price before the tip. Thus, 115% of this price equals $35.19:
1.15x = 35.19
Divide both sides by 1.15:
42. H. The sine of an angle is the length of the opposite side over the length of the hypotenuse (
). So
You know the lengths of one leg and the hypotenuse of this triangle, so use the Pythagorean theorem to find length of the remaining adjacent leg:
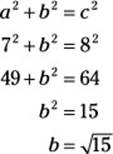
Now you can plug the values into the cosine formula:
43. B. The domain of the function can’t include a negative value inside the radical, so set the value inside the radical greater than or equal to 0 and solve for x:
The domain also can’t include 0 in the denominator, so set the denominator equal to 0 and solve for x to find excluded values:
x – 3 = 0
x = 3
The value 3 also is excluded from the domain, so x > 3.
44. J. Let a equal the number of minutes that Andrea had been waiting two minutes ago. At that time, Zach had been waiting for twice as long as Andrea, so he had been waiting for 2a minutes. Three minutes from now, both Andrea and Zach will each have been waiting for 5 minutes longer:
Three minutes from now, Andrea will have been waiting for 
as long as Zach, so make an equation as follows:
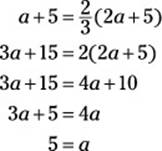
Thus, two minutes ago, at 11:28, Andrea had been waiting for 5 minutes. So she arrived at 11:23.
45. A. Let x equal the radius of a shaded circle, and then plug this value into the formula for the area of a circle:
The area of the shaded region is two of these circles, so it’s 2πx2. The shaded circles are identical, so the radius of a shaded circle is half that of the large circle. As a result, the radius of the large circle is 2x. Use the formula for the area of the circle:
You already know that 2πx2 of this area is shaded, so the other 2πx2 is not. Thus, the shaded and nonshaded regions are the same size. In other words, they’re in a 1:1 ratio.
46. K. The line that’s shown in the figure passes through (0, 0) and (1, 3), so its slope is “up 3, over 1”:
Thus, the new line that’s perpendicular to this line, and passing through P = (1, 3), will have a negative reciprocal slope, which is 
. To find the equation of this line, plug these numbers into the slope-intercept form to get b:
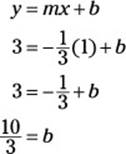
Finally, plug in the values to get the equation for this line:
47. E. To add two matrices, you add the corresponding components. So this matrix equation yields the following three equations:
6 + x = 9
x + y = 7
y + z = 5
In the first equation, x = 3. Substituting 3 for x in the second equation gives you 3 + y = 7, so y = 4. If you substitute 4 for y in the third equation, you get 4 + z = 5; therefore, z = 1. Therefore, x + y + z = 3 + 4 + 1 = 8.
48. J. To begin, add a line to the figure, cutting off a 30-60-90 triangle on the left side of the trapezoid, as shown here:
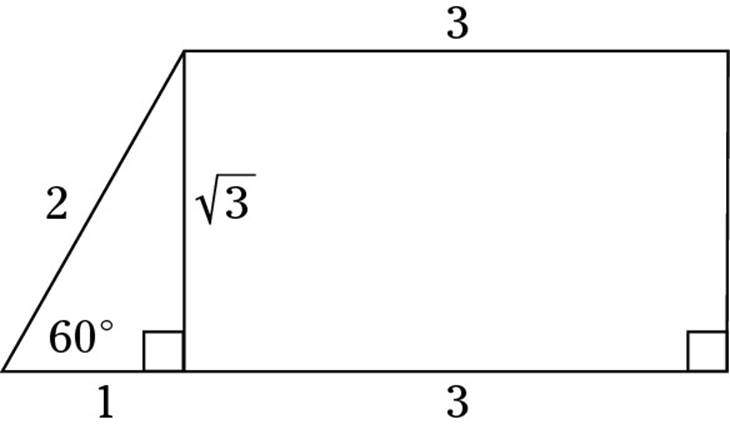
Notice that the short leg of this triangle has a length of 1, so the height of the trapezoid is 
. Plug this value, plus the lengths of the two bases, into the formula for a trapezoid to get your answer:
49. C. Place the numbers of accounts sold in order from smallest to largest:
7 8 9 10 11 12 12 14
The middle two numbers are 10 and 11, so the median is the average of these two numbers, which is 10.5.
50. J. Begin by treating the inequality x2 – x – 2 > 0 as if it were an equation. Factor to find the zeros:
x2 – x – 2 = 0
(x + 1)(x – 2) = 0
x = –1 and x = 2
The graph of this function is a parabola that crosses the x-axis at –1 and 2. This graph is concave up because the coefficient of the x2 term (that is, a) is positive. The parabola dips below the x-axis when –1 < x < 2, so these values do not satisfy the equation. Therefore, the correct answer is Choice (J). (If you doubt this answer, note that when x = 0, x2 – x – 2 = –2, which is less than 0. So 0 is not in the solution set.)
51. C. The formula for a circle with a radius r centered at (a, b) is (x – a)2 + (y – b)2 = r2. Thus, x2 + (y – 2)2 = 4 has a radius of 2 and is centered at (0, 2), as shown here:
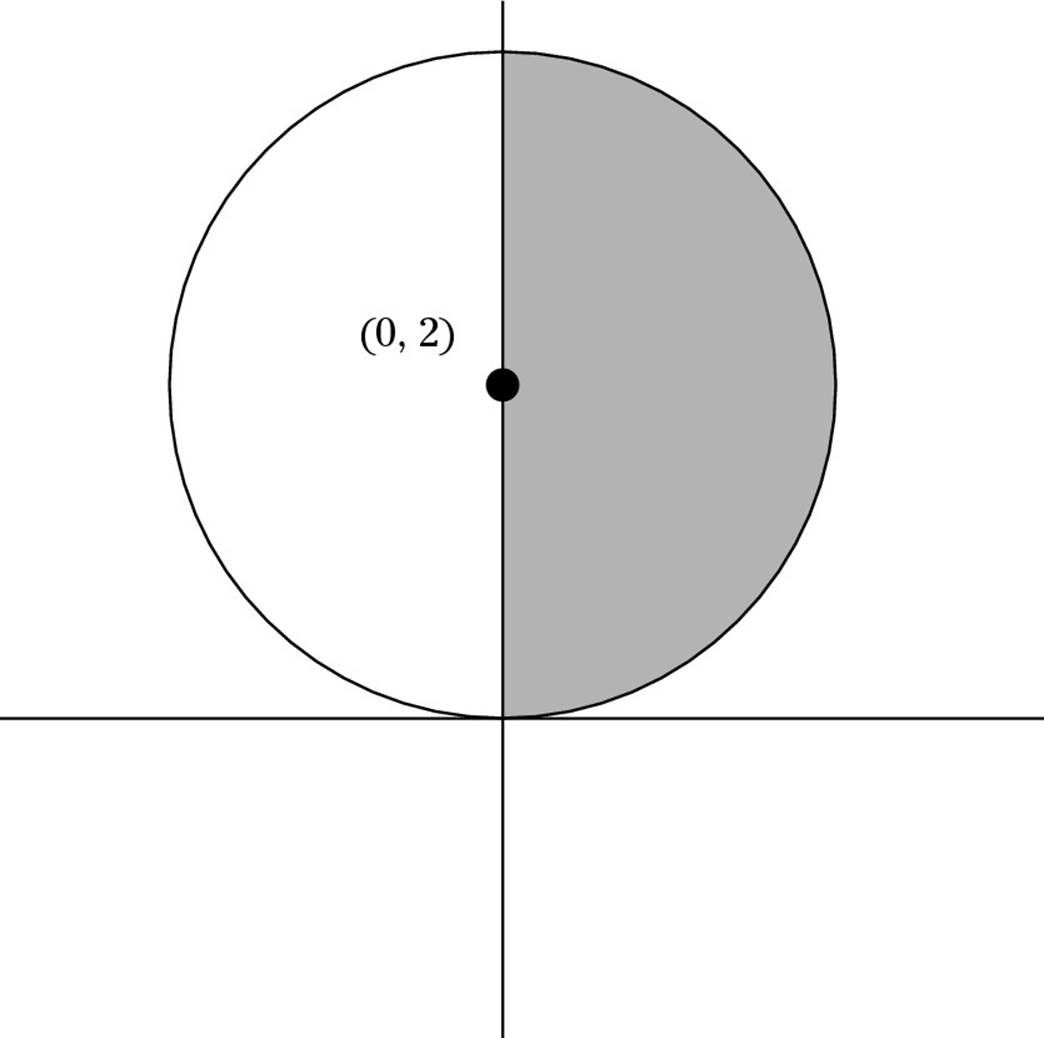
This circle has a radius of 2, so calculate its total area as follows:
Because half the circle is in Quadrant 1, the area of this region is 2π.
52. F. Begin by finding the value of 
:
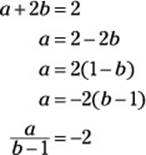
Now substitute –2 for to get your answer:
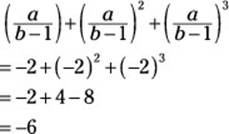
53. D. A good way to begin is to draw a picture showing the three points given, including possible places where a fourth point would form a parallelogram. Here’s what your picture may look like:
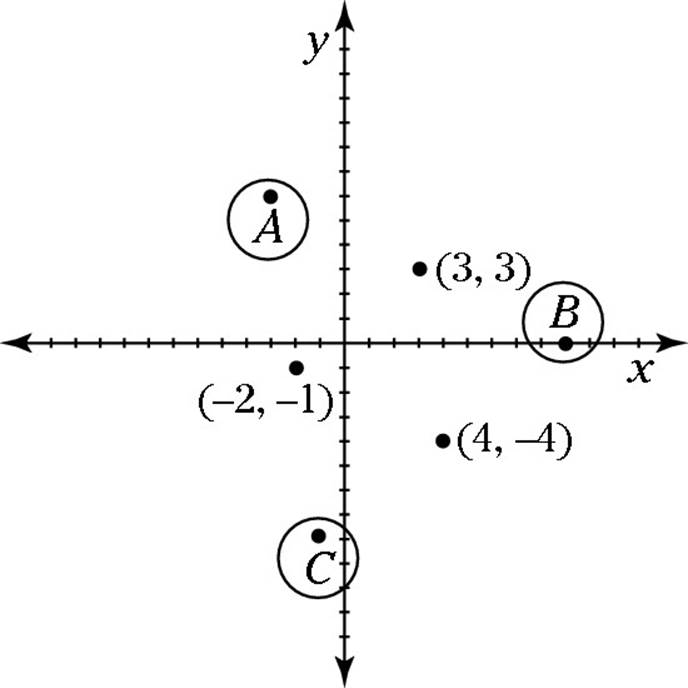
This figure shows three possible points for the remaining corner of the parallelogram: A, B, and C. To find the exact coordinates of these three additional points, choose any of the given points and count up and over (or down and over) to a second given point. Then, starting from the third given point, count the same number of steps up and over (or down and over) and label the point where you end up.
By this method, you find that A = (–3, 6), B = (9, 0), and C = (–1, –8). Only point A is listed as an answer.
54. G. Doug runs 2 miles an hour faster than Matt, so let Matt’s speed equal x miles per hour. Then Doug’s speed equals x + 2 miles per hour. Each lap is one-quarter of a mile, so Doug runs 1.5 miles in the time it takes Matt to run 1.25 miles. Place this information in a chart:
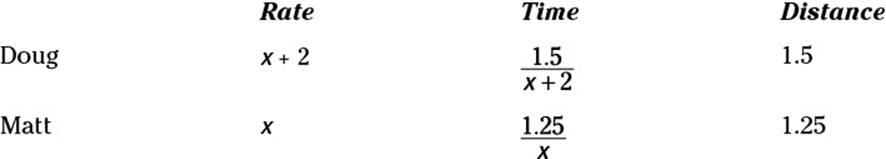
The two boys took the same amount of time from the time Doug started, so make an equation by setting the two times in the chart equal to each other, and then solve for x:
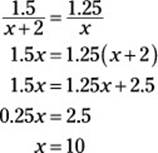
So Matt ran at 10 miles per hour.
55. B. For income less than p dollars, the tax rate is $0, so the line should begin at the origin; therefore, you can rule out Choices (A) and (E). For income greater than p dollars, the tax rate increases at a steady rate without leveling off, so you can rule out Choices (C) and (D). By elimination you know that the correct answer is Choice (B).
56. H. The amplitude is the vertical distance from the midpoint to the crest, so in this case it’s 5. The period is the horizontal distance between two adjacent crests, so it’s 4π.
57. E. Given that the equation x2 + mx + n = 0 has two solutions, x = k and x = 2k, you can work backward to build the original equation. Here’s how:
x = k x = 2k
x – k = 0 x – 2k = 0
Now take the two equations and combine them:
(x – k)(x – 2k) = 0
x2 – 2kx – kx + 2k2 = 0
x2 – 3kx + 2k2 = 0
As you can see, m = –3k and n = 2k2, so mn = –6k3.
58. H. The first character of the password can be any letter or number, so Eloise has ten options. Her second choice must be from the set (letter or number) not yet used, so she has five options. Choice 3 is from the same set as Choice 1, and she has four options left. Choice 4 is the second item from the same set as Choice 2, so she has four options. Choices 5 and 6 are from different sets, each with three options; Choices 7 and 8 are from different sets, each with two options; Choices 9 and 10 are from different sets, each with only one option remaining. You can see this information in the following chart:
1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th
10 5 4 4 3 3 2 2 1 1
To find the total number of possible passwords, multiply these numbers together:
10 × 5 × 4 × 4 × 3 × 3 × 2 × 2 × 1 × 1 = 28,800
59. C. To begin, notice that 540 isn’t a multiple of 24, so you can rule out Choice (B). Now find the least common multiple (LCM) of 9, 10, and 12. The LCM of 9 and 10 is 90, so the LCM of 9, 10, and 12 must be a multiple of 90. Here are the first six multiples of 90:
90, 180, 270, 360, 450, 540
The number 180 is a multiple of 12 as well, so the LCM of 9, 10, and 12 is 180. However, 180 also is a multiple of 18, 36, and 45. So if any of these numbers were v, the LCM of 9, 10, 12, and v would be 180. As a result, you can rule out Choices (A), (D), and (E), leaving Choice (C) as your only answer.
60. H. To begin, plug x = 0 and y = 2 into the equation y = axb + c. Note that the first term drops out:
2 = a(0)b + c
2 = c
Now you can substitute 2 for c in the original equation, giving you y = axb + 2. Next, plug in x = 1 and y = 7. Notice that everything drops out except for the coefficient of the first term:
7 = a(1)b + 2
5 = a
You can now substitute 5 for a in the equation, giving you y = 5xb + 2. Now plug in x = 2 and y = 42:
42 = 5(2)b + 2
40 = 5(2)b
8 = 2b
23 = 2b
3 = b
Finally, you can see that abc = (5)(3)(2) = 30.
Answer Key for Practice Test 1
1. D
2. H
3. D
4. F
5. E
6. F
7. B
8. J
9. B
10. J
11. C
12. H
13. C
14. H
15. C
16. J
17. B
18. F
19. D
20. G
21. B
22. K
23. C
24. J
25. D
26. J
27. E
28. K
29. E
30. F
31. A
32. K
33. D
34. H
35. D
36. J
37. C
38. G
39. B
40. G
41. D
42. H
43. B
44. J
45. A
46. K
47. E
48. J
49. C
50. J
51. C
52. F
53. D
54. G
55. B
56. H
57. E
58. H
59. C
60. H