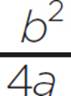High School Algebra I Unlocked (2016)
Chapter 6. Quadratic Equations and Inequalities
GOALS
By the end of this chapter, you will be able to:
•Explain how quadratic equations can model real-life situations
•Identify the graphs of quadratic, cubic, quartic, and quintic equations
•Solve quadratic equations and quadratic inequalities using methods such as factoring, completing the square, and the quadratic formula
•Graph quadratic equations and inequalities
•Determine the vertex and axis of symmetry of quadratic equations and inequalities
•Determine the number of solutions of a quadratic using the discriminant
•Solve linear-quadratic systems of equations
Lesson 6.1. Introduction to Quadratic Equations
So far in this book we’ve focused on linear equations, or equations that extend in a straight line. While linear equations can be used to determine the linear relationship of variables and show the rate at which things change, they are limited in their use. In the real world, there are many occurrences that are not linear.
For example, what if you wanted to know how long a tissue would float in the air before hitting the ground? Or, what if you wanted to model the speed of a lizard as it runs through a maze? Or, better yet, imagine you’re planning an epic snowball fight. You’ve already built your snow igloo and formed the snowballs, but you want to know how long it will take for your snowball to hit your opponent, Donald.
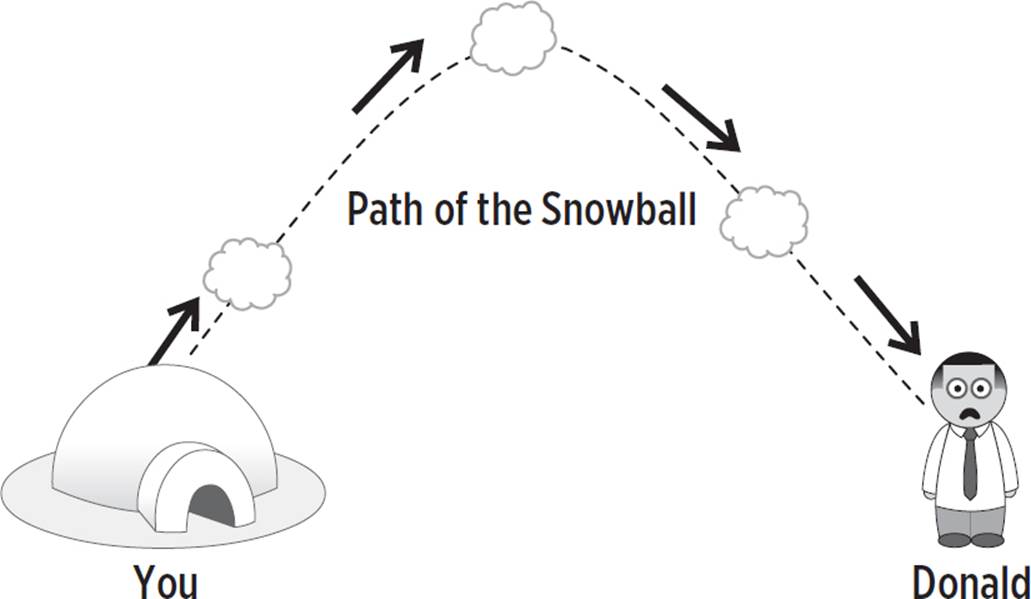
In these scenarios, you would not be able to use a linear equation to model the situation. Instead, you would use a quadratic equation. A quadratic equation is an equation in the form ax2 + bx + c and has a squared term as the highest degree term. Quadratic equations are useful for finding all sorts of everyday things like speed, profit, and area.
Why is it called a
quadratic? In Latin, the
word quadrus means
“square.” Since a
quadratic equation in
the form ax2 + bx + c has
a squared term, some
mathematicians deemed
all equations quadratics.
Since we covered quadratic expressions in Chapter 3, you should be familiar with the standard form of a quadratic expression: ax2 + bx + c. The standard form of a quadratic equation is ax2 + bx + c = 0, where x is the variable, a, b, and c are constants, and a ≠ 0. A quadratic equation has a degree of 2 and contains at least one squared term, with no term having an exponent greater than two.

Refer back to Chapter 3
to re-familiarize yourself
with polynomials and
quadratic expressions.
All of the following are quadratic equations and their associated graphs:
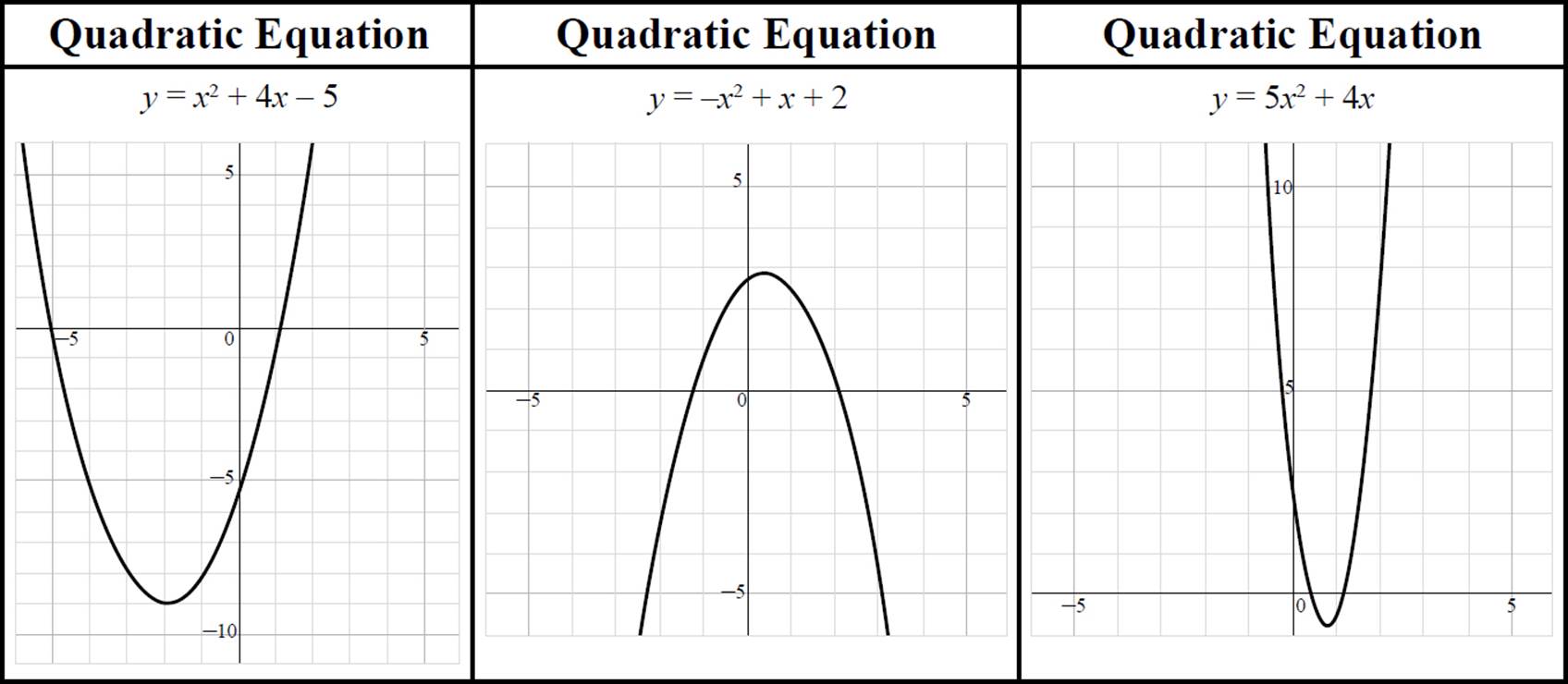
Notice that all of the quadratic equations are graphed as curves—the curve created by a quadratic equation is known as a parabola.
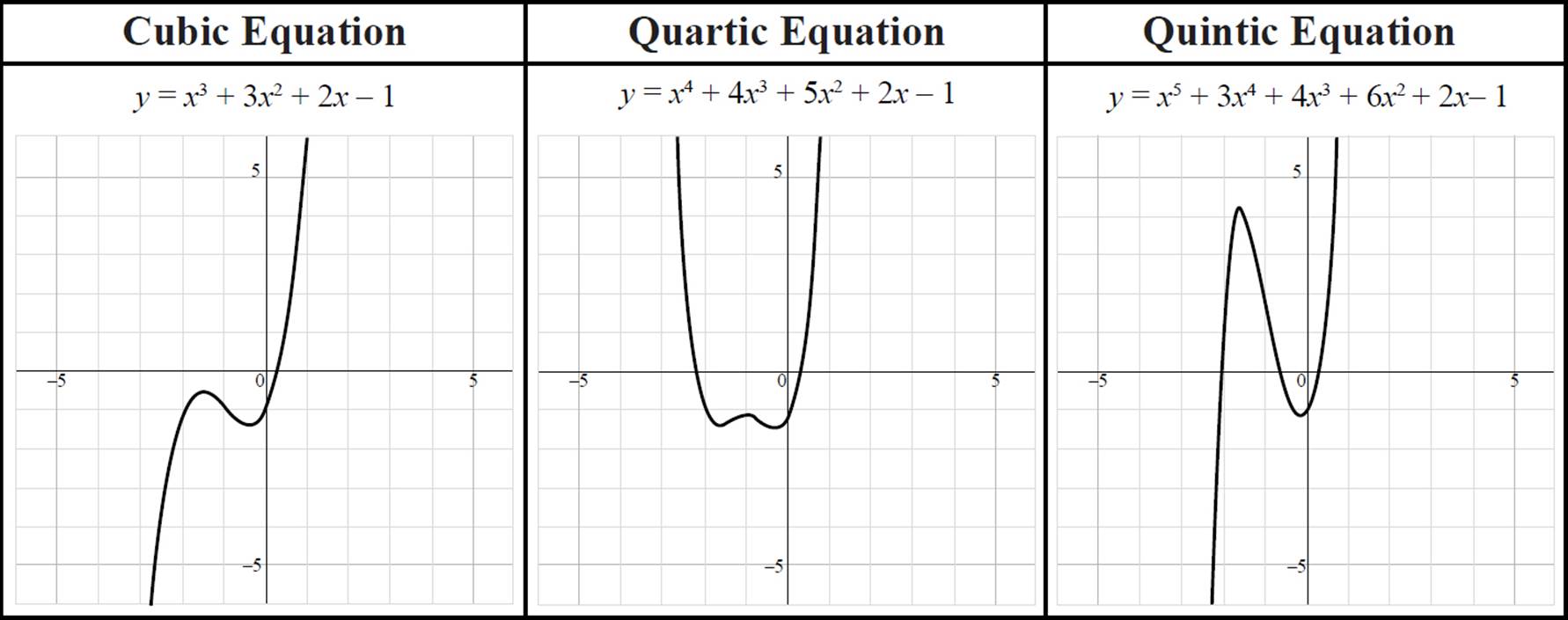
Non-quadratic equations do not have the parabola shape. Take a look at the following examples of cubic, quartic, and quintic equations and their graphs:
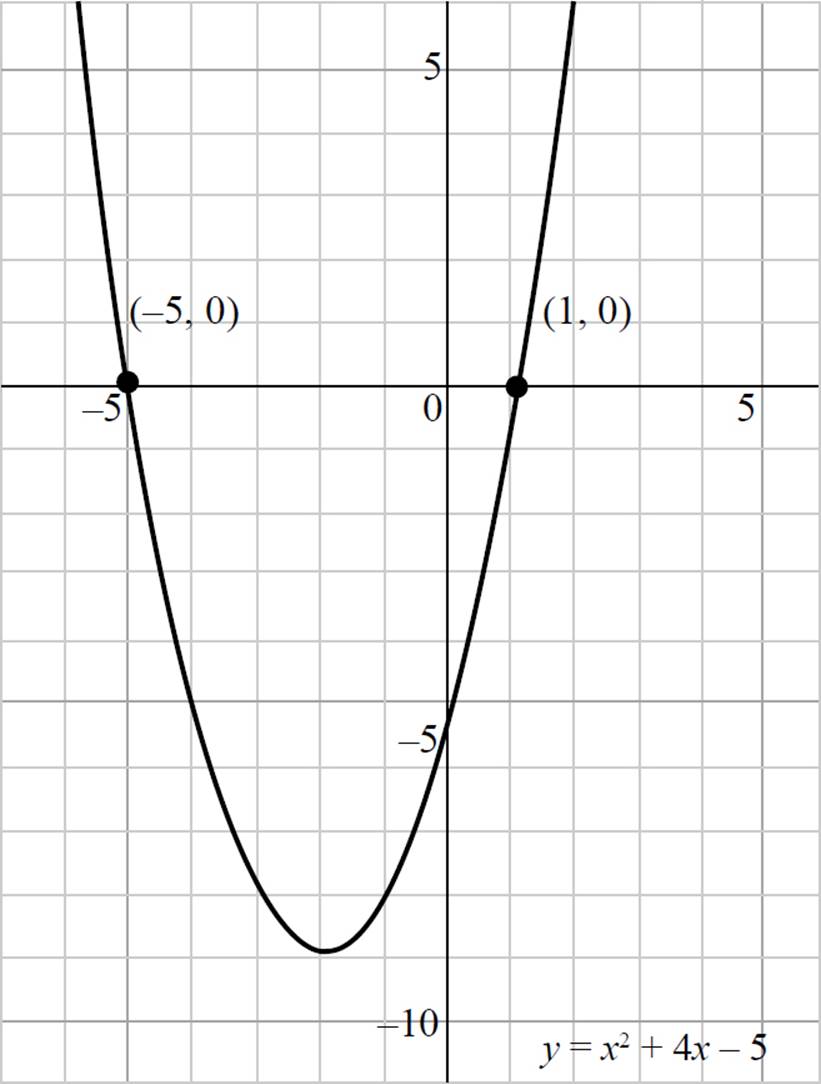
Let’s take a closer look at the quadratic equation we graphed above, y = x2 + 4x − 5. Here, the parabola crosses the x-axis at two points, (−5, 0) and (1, 0); these are the solutions of the quadratic equation. The solutions of a quadratic equation, also referred to as the roots or zeros of a quadratic, are the points where the equation is equal to zero.
The Latin roots continue!
A cubic equation has a
degree of 3 and at least
one x3 term, a quartic
equation has a degree of
4 and at least one x4 term,
and a quintic equation
has a degree of 5 and
at least one x5 term.
There are three ways to find the roots of a quadratic equation: factoring, completing the square, or the quadratic formula. Luckily, we already covered factoring quadratics and completing the square, so this should not be too intimidating.

Do you need to review
factoring and completing
the square? If so, flip
back to Lesson 3.4!
Three Methods for Finding the Roots of a Quadratic Equation
1) Factoring the quadratic expression
2) Completing the square
3) Using the quadratic formula: x = 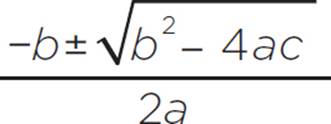
Let’s refresh our memory about the rules for factoring quadratic expressions. When factoring quadratics in the form ax2 + bx + c, if a = 1, then ax2 + bx + c = (x + m)(x + n), where m and n are factors of c, and m + n = b.
• If the value of c is positive, both m and n are either positive or negative.
○ If the value of b is positive, both m and n will be positive.
○ If the value of b is negative, both m and n will be negative.
• If the value of c is negative, m and n will have different signs.
○ If the value of b is positive, the larger factor will be positive.
○ If the value of b is negative, the larger factor will be negative.
Once we’ve factored the quadratic, we can enact the power of the zero product property, which states that if a × b = 0, then a = 0, b = 0, or both a = 0 and b = 0. The zero product property would indicate that if (x + 2)(x + 6) = 0, then (x + 2) = 0 or (x + 6) = 0, and x = −2 or x = −6.
Let’s try a question that deals with factoring a quadratic and using the zero product property.
EXAMPLE 
Solve x2 + 5x + 6 = 0 by factoring.
When factoring quadratic equations, start by setting up your initial terms. Here, the first term is x2, so the initial parentheses will be set up as follows:
x2 + 5x + 6 = (x )(x )
Next, find factors of the c-term, 6, that add up to the b-term, which is 5. In this scenario, both b and c are positive, so both factors will be positive. Make a chart like the following:
|
Factors of c-term (6) |
Sum of the Factors |
Value of b-term (5) |
|
1, 6 |
1 + 6 = 7 |
5 |
|
2, 3 |
2 + 3 = 5 |
5 |
In the chart, the only factors of the c-term, 6, that add up to the b-term, 5, are 2 and 3. Therefore, we can fill in the rest of the parentheses like this:
x2 + 5x + 6 = (x + 2)(x + 3)
Now that we’ve factored the quadratic, solve for x using the zero product property: Take each parenthetical term, set it equal to zero, and solve for x.
|
(x + 2) |
(x + 3) |
|
x + 2 = 0 |
x + 3 = 0 |
|
x = −2 |
x = −3 |
Thus, the solutions, or zeros, of the quadratic equation x2 + 5x + 6 = 0 are x = −2 and −3.
Notice that the solutions to a quadratic are simply the numbers found within the factored parentheses with the opposite sign. For example, if the quadratic is factored as (x + 2)(x − 3), the roots of the equation are x = −2 or x = 3. On the other hand, if you know that the roots of a quadratic equation are x = −2 or x = 3, you know that it will be factored as (x + 2)(x − 3). Knowing these tidbits can save you time!

It’s possible to have a quadratic equation with a double root, or two identical roots. A quadratic equation that has a b-term that is twice the square root of the c-term will have a double root. Let’s see an example.
EXAMPLE 
Solve x2 − 10x + 25 = 0 by factoring. State whether or not the quadratic equation has a double root.
Here we have the quadratic equation x2 − 10x + 25 = 0. In this scenario, the b-term, 10, is twice the square root of the c-term, since ![]() = 5. You should recognize this as a double root quadratic, so set up the initial parentheses as follows:
= 5. You should recognize this as a double root quadratic, so set up the initial parentheses as follows:
x2 − 10x + 25 = (x − 5)(x − 5)
Using the zero product property, you can now find the roots of the quadratic:
x − 5 = 0
x = 5
In this case, the quadratic has a double root at x = 5.
If you didn’t know the rules of double roots, it’s still possible to solve the problem. Factor as you normally would to find factors of the c-term, 25, that add up to the b-term, which is −10. Based on the rules for factoring quadratics, if the value of the c-term is positive and the value of the b-term is negative, the factors m and n will both be negative. Thus, our chart would look like this:
|
Factors of c-term (25) |
Sum of the Factors |
Value of b-term (−10) |
|
−1, −25 |
−1 + (−25) = −26 |
−10 |
|
−5, −5 |
−5 + (−5) = 10 |
−10 |
In the chart, the only factors of the c-term, 25, that add up to the b-term, −10, are −5 and −5. Thus, factor the quadratic as follows:
x2 − 10x + 25 = (x − 5)(x − 5)
Now solve for x using the zero product property:
x − 5 = 0
x = 5
Thus, the quadratic equation x2 − 10x + 25 = 0 has a double root at x = 5.

You may also have to use the zero product property to find the solutions of a quadratic equation that is not initially in standard form, ax2 + bx + c = 0. Let’s see how a question like this would work.
EXAMPLE 
Find the roots of x2 = 4x by converting the quadratic to standard form and factoring.
While you may be tempted to divide both sides of the equation by x to simplify, don’t fall into the trap! If x = 0, and you divide both sides by x, you would be dividing by 0 which, as you know, is a major math faux pas. Instead, start by rewriting the quadratic into standard form:
x2 = 4x
x2 − 4x = 0
Then factor the quadratic as you normally would, noting that there is no c-term in this quadratic equation. Therefore, you can only factor out an x:
x2 − 4x = 0
x(x − 4) = 0
Now that you’ve factored the quadratic, solve for x using the zero product property by taking each x-term, setting it equal to zero, and solving for x, as shown below.
|
x |
(x − 4) |
|
x = 0 |
x − 4 = 0 |
|
x = 4 |
Thus, the roots of the quadratic equation x2 − 4x = 0 are x = 0 or x = 4.

Another way to find the solutions of a quadratic equation is by completing the square.
|
Standard Quadratic Form |
Completing the Square |
|
ax2 + bx + c |
a(x + d)2 + e |
|
d = |
Once you’ve put the quadratic equation in the form used to complete the square, you simply need to solve for x.
In addition to identifying the solutions of a quadratic equation by completing the square, you can also find the axis of symmetry, which is a vertical line that splits a parabola into two symmetrically parts along the vertex, which is the minimum or maximum point of a quadratic.
The vertex form of a quadratic is written as y = a(x − h)2 + k, where (h, k) is the vertex.
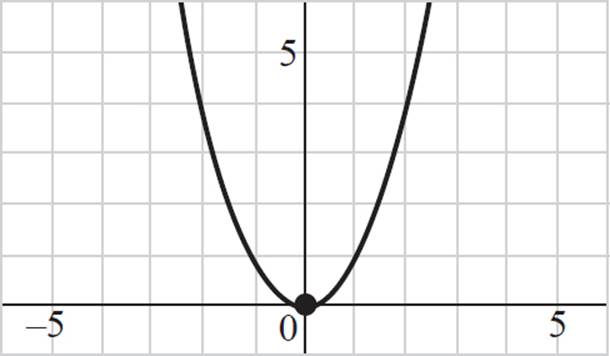
If the value of a is positive, the graphed quadratic will resemble a smile:
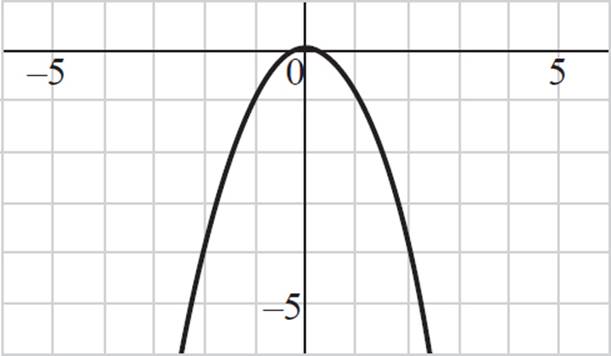
If the value of a is negative, the quadratic will resemble a frown.
The axis of symmetry for any quadratic in the form ax2 + bx + c is equal to x = −b/2a.
Notice that the vertex form of a quadratic is almost identical to the quadratic form associated with completing the square. The difference? Instead of using the variables d and e, the vertex form of a quadratic uses the variables h and k. Accordingly, if you can factor a quadratic by completing the square, you know that the vertex of that quadratic is (d, e), which is the same thing as (h, k).
EXAMPLE 
Find the vertex, axis of symmetry, and roots of y = 3x2 + 6x − 7 by completing the square.
We are given the quadratic 3x2 + 6x − 7 and, since the standard form of a quadratic expression is ax2 + bx + c, we know that a = 3, b = 6, and c = −7. We need to find the values of d and e to complete the square and factor the quadratic in the form a(x + d)2+ e.
Using the values of a, b, and c and the formulas given previously, we can find the value of d:
d = 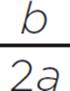
d = ![]()
d = 1
Then find the value of e, substituting the values of a, b, and c:
e = c −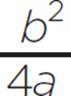
e = −7 −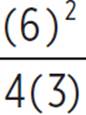
e = −7 −![]()
e = −7 − 3
e = −10
Now substitute the values a = 3, d = 1, and e = −10 into the quadratic form associated with completing the square:
a(x + d)2 + e =
3(x + 1)2 +(−10)
3(x + 1)2 − 10

Here is how you may see quadratic equations on the ACT.
What is the largest value of x that solves the equation x2 − 4x + 3 = 0 ?
A. 1
B. 2
C. 3
D. 4
E. 5
Once you’ve factored by completing the square, set the factored expression equal to zero, simplify the equation, and solve for x:
3(x + 1)2 − 10 = 0
3(x + 1)2 = 10
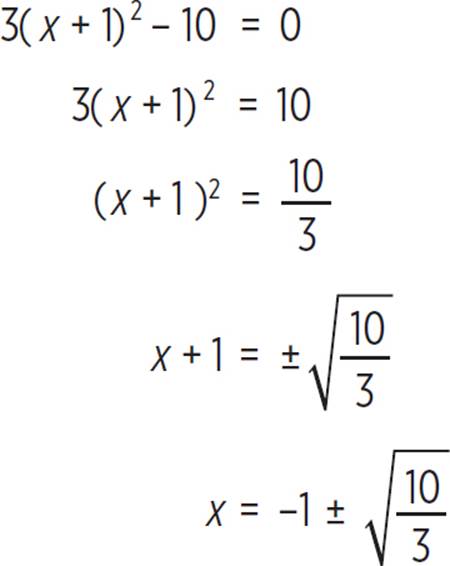
Don’t forget—you can’t have a radical in the denominator. Get rid of that radical by multiplying 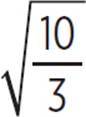 by
by 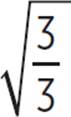 , which is 1.
, which is 1.
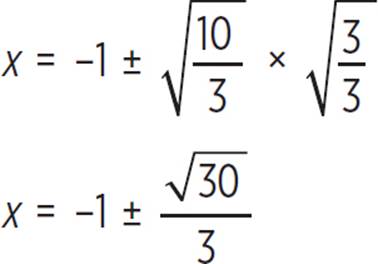
Finally, you have found that the roots of the quadratic equation 3x2 + 6x − 7 = 0 are x = −1 ± 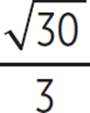 , which is expressed in decimal form as x = −2.826 or x = 0.826.
, which is expressed in decimal form as x = −2.826 or x = 0.826.
However, you also need to identify the axis of symmetry and the vertex of the quadratic. Here, the quadratic, written as 3(x + 1)2 − 10 = 0, is similar to the vertex form of a quadratic, y = a(x − h)2 + k, where (h, k) is the vertex. Thus, the quadratic 3(x + 1)2 − 10 = 0 can be rewritten in vertex form as 3(x − (−1))2 + (−10), meaning that the value of h = −1, the value of k = −10, and the vertex of the quadratic equation is (−1, −10).
After identifying the vertex of the quadratic equation, you can find the axis of symmetry, which is dependent upon the x-value of the vertex. Since the vertex is (−1, −10), the axis of symmetry of the quadratic 3(x + 1)2 − 10 = 0 is x = −1.
Therefore, the quadratic equation 3x2 + 6x − 7 = 0 has a vertex of (−1, −10), an axis of symmetry of x = −1, and roots x = −2.826 or x = 0.826.

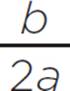 and e = c −
and e = c −