High School Algebra I Unlocked (2016)

Lesson 6.2. The Quadratic Formula

One of the formulas that you (hopefully) will forever remember after taking algebra is the quadratic formula. As you might imagine, the quadratic formula is closely linked to quadratic equations. Up until now, we’ve been finding the roots and solutions to quadratic equations by factoring or completing the square. Sometimes, however, it is not efficient to use these methods. In such instances, you will use the quadratic formula, x = 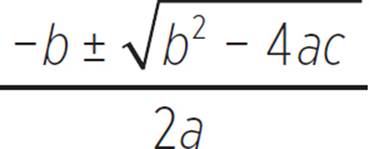, which is used to find the roots of quadratic equations. As you know, the standard form of a quadratic equation is ax² + bx + c = 0. Using the information about a, b, and c from a quadratic equation, you can use this formula to solve for x. Furthermore, you can find the vertex, axis of symmetry, and solutions of a quadratic equation by using the quadratic formula.

Here you are asked to find the largest value of x that solves the equation x² − 4x + 3 = 0. While the phrasing of the question stem may be different than the questions we’ve tackled so far, you are still looking for the solutions, or roots, of the equation. Since the value of the c-term is positive and the value of the b-term is negative, you know that the factors of the quadratic will both be negative. Therefore, your factor chart will look like this:

Since the c-term was a prime number it had only one set of factors, −1 and −3, which is written in factored form as (x − 1)(x − 3). Based on the zero product property, you know that x = 1 and x = 3. However, since the question asks for the largest value of x, the correct answer is 3, or (C).

The quadratic formula: x = .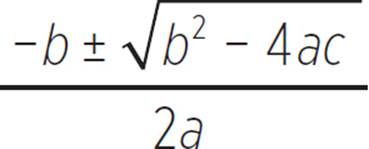

The vertex (h, k) for any quadratic ax² + bx + c can be determined with (h, k) = (−, ).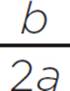

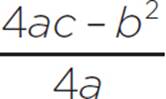The axis of symmetry for any quadratic ax² + bx + c can be determined with x = −.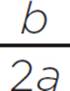

Let’s try some questions.

EXAMPLE

Use the quadratic formula to identify the vertex, the axis of symmetry, and the roots of y = −x² + 2x + 3.

Unlike the previous questions, which required us to use methods based on factoring, the quadratic formula does not require factoring. Here we’re given a quadratic, −x² + 2x + 3, and asked to find the roots of the equation using the quadratic formula. Since the standard form of a quadratic expression is ax² + bx + c, we know that a = −1, b = 2, and c = 3. So plug those values into the quadratic equation and simplify:

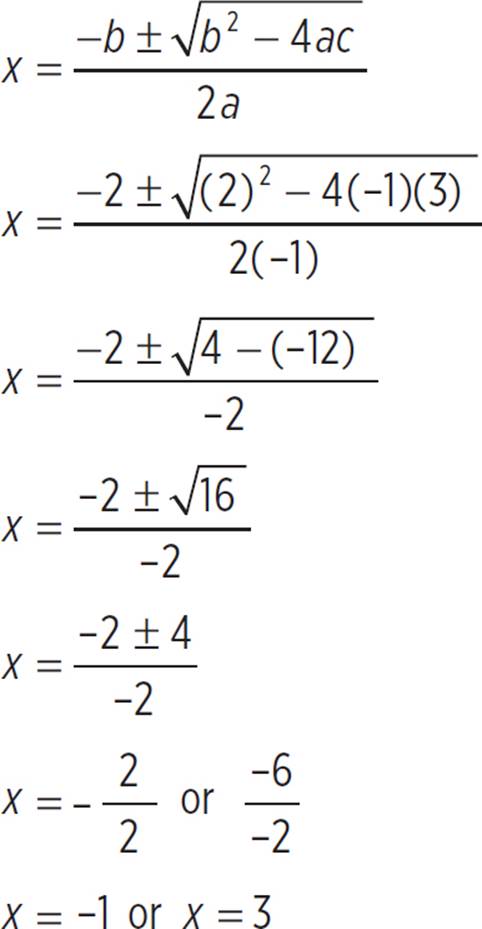
The roots of the quadratic equation −x² + 2x + 3 = 0 are x = −1 or x = 3.

Every positive number
has both a positive and
negative square root:
for example, x² = 16 and
x = ±4. So, if you solve
an equation by taking
the square root of both
sides, you must account
for both the positive and
negative solutions:

(x + 2)² = 5

x + 2 = ±

x = −2 ±

Now determine the vertex (h, k) of the quadratic equation, which is equal to (−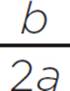, 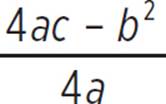). In our quadratic equation y = −x² + 2x + 3, we know that a = −1, b = 2, and c = 3. Therefore, the vertex (h, k) of the quadratic equation is (−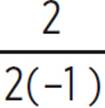, 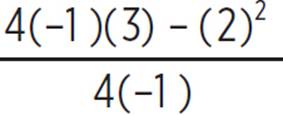), (−, ), 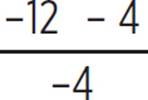(1, 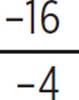) and (1, 4).

Finally, since the axis of symmetry of a quadratic equation is equal to x = −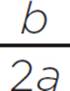, we can look at the value of h in the vertex to determine that the axis of symmetry is equal to x = 1.

Thus, the vertex of the quadratic equation y = −x² + 2x + 3 is (1, 4), the axis of symmetry is x = 1, and the roots are x = −1 or x = 3.

EXAMPLE

Use the quadratic formula to identify the vertex, the axis of symmetry, and the zeros of y = 2x² − 11x + 5.

Here we’re given the quadratic 2x² − 11x + 5 and, because the standard form of a quadratic expression is ax² + bx + c, we know that a = 2, b = −11, and c = 5. Now just plug those values into the quadratic equation and simplify:

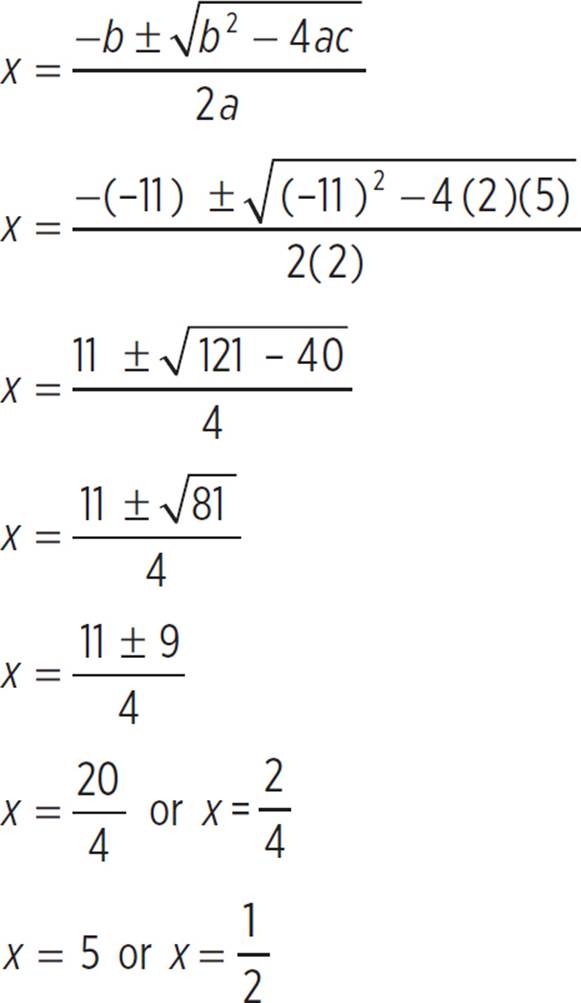
So, we find that the zeros of the quadratic equation 2x² − 11x + 5 = 0 are x = 5 or x = .

Next, you need to find the vertex (h, k) of the quadratic equation, which is equal to (−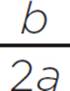, 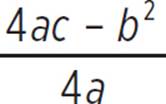). In the quadratic equation y = 2x² − 11x + 5, we know that a = 2, b = −11, and c = 5. Therefore, the vertex (h, k) of the quadratic equation is (−, 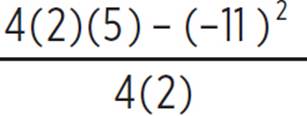), (, ), 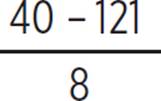(2.75, 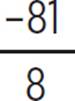), which equals (2.75, −10.13).

Now you can determine that the axis of symmetry, which is equal to x = − 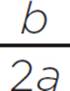, of the quadratic equation y = 2x² − 11x + 5 is equal to x = 2.75.

Therefore, the vertex of the quadratic equation y = 2x² − 11x + 5 is (2.75, −10.13), the axis of symmetry is x = 2.75, and the roots are x = 5 or x = 1/2.

Thus far, we have solved quadratic equations that have two real solutions. But you don’t always get two answers when solving a quadratic equation. In order to determine the number of solutions of a quadratic equation, you can use thediscriminant, or the value b² − 4ac.

The discriminant is b² − 4ac.

• If the discriminant is positive, the quadratic equation will have two real solutions.

• If the discriminant is zero, the quadratic equation will have one real solution.

• If the discriminant is negative, the quadratic equation will have two complex solutions, or solutions that include the imaginary number i.

An extraneous solution is a solution that emerges when solving an equation, but is not a valid solution in the original equation.

Let’s try out a couple of questions that deal with all of these mathematical terms.

Complex solutions are
those that include the
imaginary number i.
While you won’t have
to deal with imaginary
numbers until Algebra
II (check out our High
School Algebra II
Unlocked!), you can get
a head start by
memorizing the rules
of i:

i¹ = i

i² = −1

i³ = −i

i⁴ = 1

And then the
cycle repeats!

EXAMPLE

Use the discriminant to determine the number of real solutions in the quadratic equation 4x² + 4x + 1 = 0, and then find the real solution(s).

Here we’re given the quadratic 4x² + 4x + 1 = 0 and asked to determine the number of solutions using the discriminant, which is b² − 4ac. Since the standard form of a quadratic expression is ax² + bx + c, we know that a = 4, b = 4, and c = 1. Plug those values into the discriminant formula and simplify:

 b² − 4ac =

4² − 4(4)(1) =

 16 − 16 = 0

Since the discriminant is 0, the quadratic has one real solution. In order to find the solution, you can use the quadratic formula:

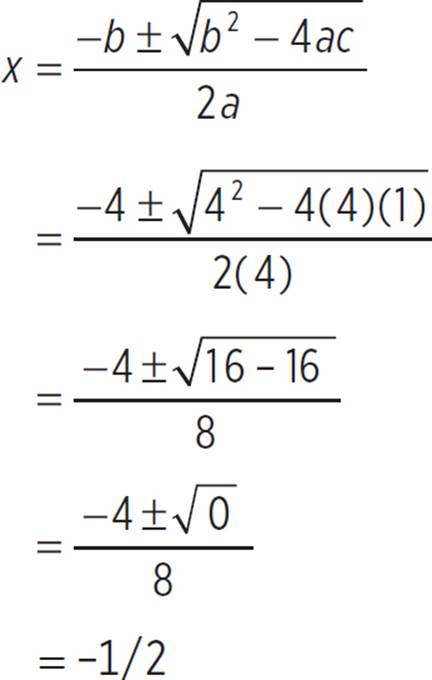
Thus, since the value of the discriminant is zero, there was one real solution at x = −1/2.

Here is how you may see quadratic equations on the SAT.

In this expression x² + kx + 12, k is a negative integer. Which of the following is a possible value of k ?

A) −13

B) −12

C) −6

D) 7

EXAMPLE

Use the discriminant to determine the number of real solutions in the equation 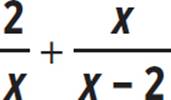= 4 and then find the real solutions.

Here we’re given the equation 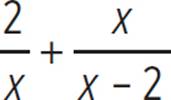= 4 and asked to determine the number of solutions using the discriminant, which is b² − 4ac. Put the equation in the standard form of a quadratic expression, which is ax² + bx + c = 0. Since the common denominator in this equation is x(x −2), the equation becomes

2(x − 2) + x(x) = 4(x)(x − 2)

2x − 4 + x² = 4x(x − 2)

2x − 4 + x² = 4x² − 8x

3x² − 10x + 4 = 0  

Therefore, we know that a = 3, b = −10, and c = 4. Now plug those values into the discriminant formula and simplify:

b² − 4ac =

(−10)² − 4(3)(4) =  

100 − 48 = 52

Since the discriminant is 52, which is a positive value, the quadratic has two real solutions. In order to solve for the solutions, use the quadratic formula as follows:

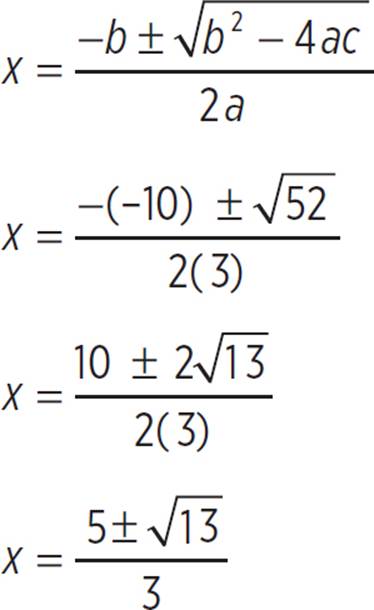
Thus, the two real solutions of the quadratic equation 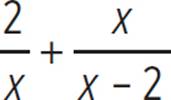= 4 are x = .

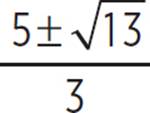Great work! You are now a master of solving quadratic equations by factoring, completing the square, and using the quadratic formula. Now let’s expand on this topic further by discussing quadratic inequalities.