High School Algebra I Unlocked (2016)
Chapter 9. Manipulating Functions
Lesson 9.3. Reflections
In Chapter 7, we discussed that the value of a in a quadratic function determines whether the parabola opens upwards or opens downwards. In the function ƒ(x) = ax2 + bx + c, the parabola will open upward if a is positive. If a is negative, the parabola will be reflected across the x-axis and open downward. A reflection is a graph that results from flipping the original graph over a line.
The function ƒ(x) = x2 reflected across the x-axis as −ƒ(x) results in the following graphs:
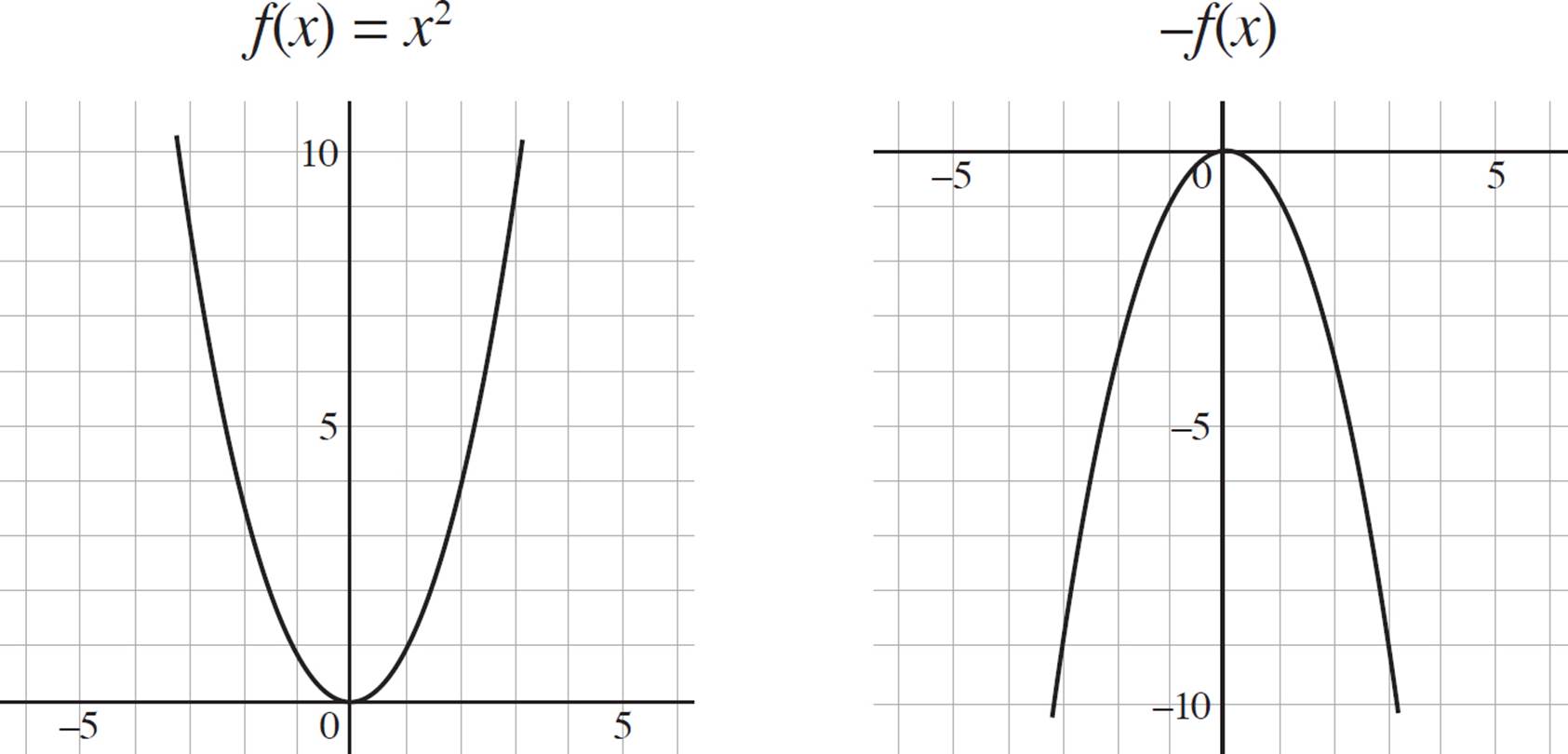
Now, here’s where it gets a little crazy. If we were to then reflect the graph of −ƒ(x) across the x-axis, the resulting graph would be the original graph of ƒ(x); a reflection of a reflection is the original graph.
You can also reflect an image across the y-axis, negating each instance of x in the function equation. Given the function ƒ(x) = x2, the image of ƒ(−x) would be identical to the pre-image when reflected over the y-axis, due to the symmetrical nature of the parabola and its location on the y-axis.
The fact that ƒ(x) =ƒ(−x) is no small thing. In fact, you may encounter questions that ask you to determine whether a function is even or odd. But what does that mean? Whenever you have a function where ƒ(x) = ƒ(−x), the function is considered even; this means that the function is symmetrical about the y-axis. If you find that ƒ(−x) = −ƒ(x), the function is considered odd. And if neither ƒ(x) = ƒ(−x) norƒ(−x) = −ƒ(x), the function is considered neither even or odd.
For any function ƒ(x), if ƒ(x) = ƒ(−x), the function is even.
For any function ƒ(x), if ƒ(−x) = −ƒ(x), the function is odd.
For any function ƒ(x), if ƒ(x) ≠ ƒ(−x) and ƒ(−x) ≠ −ƒ(x), the function is neither even or odd.
EXAMPLE 
Determine algebraically whether the function v(x) = (x − 2)2 is even, odd, or neither.
In order to determine if a function is even, odd, or neither, plug in −x to the function v(x) = (x − 2)2, and then simplify as follows:
v(x) = (x − 2)2
v(−x) = (−x − 2)2
v(−x) = (−x − 2) (−x − 2)
v(−x) = x2 + 2x + 2x + 4
v(−x) = x2 + 4x + 4
v(−x) = (x + 2)2
In this scenario, ƒ(x) ≠ ƒ(−x) and ƒ(−x) ≠ −ƒ(x), so the function is neither even or odd.

EXAMPLE 
Determine algebraically whether the function z(x) = 2x2 − 3 is even, odd, or neither.
Just like in the previous example, plug in −x to the function z(x) = 2x2 − 3 and simplify to determine if a function is even, odd, or neither.
z(x) = 2x2 − 3
z(−x) = 2(−x)2 − 3
z(−x) = 2x2 − 3
That’s all there is to it! Here, we found that z(−x) = z(x), indicating that the graph of z(x) is identical to the graph of z(−x). Thus, the function z(x) is even.

Are you struggling to
understand that, given the
function ƒ(x) = x2,
ƒ(x) = ƒ(−x)? Draw the
graph of ƒ(x) = x2 onto a
piece of paper, and fold
the paper along the y-axis.
If you hold the paper up
to the light you should see
a single line…because of
symmetry! Alternatively,
if you plug in −x for x in
the function ƒ(x) = x2, you
will find that ƒ(−x) = x2.
Thus, since ƒ(x) = ƒ(−x),
the function is even.
Let’s now consider the function h(x) = x3 + 4 and its reflection over the x-axis, −h(x).
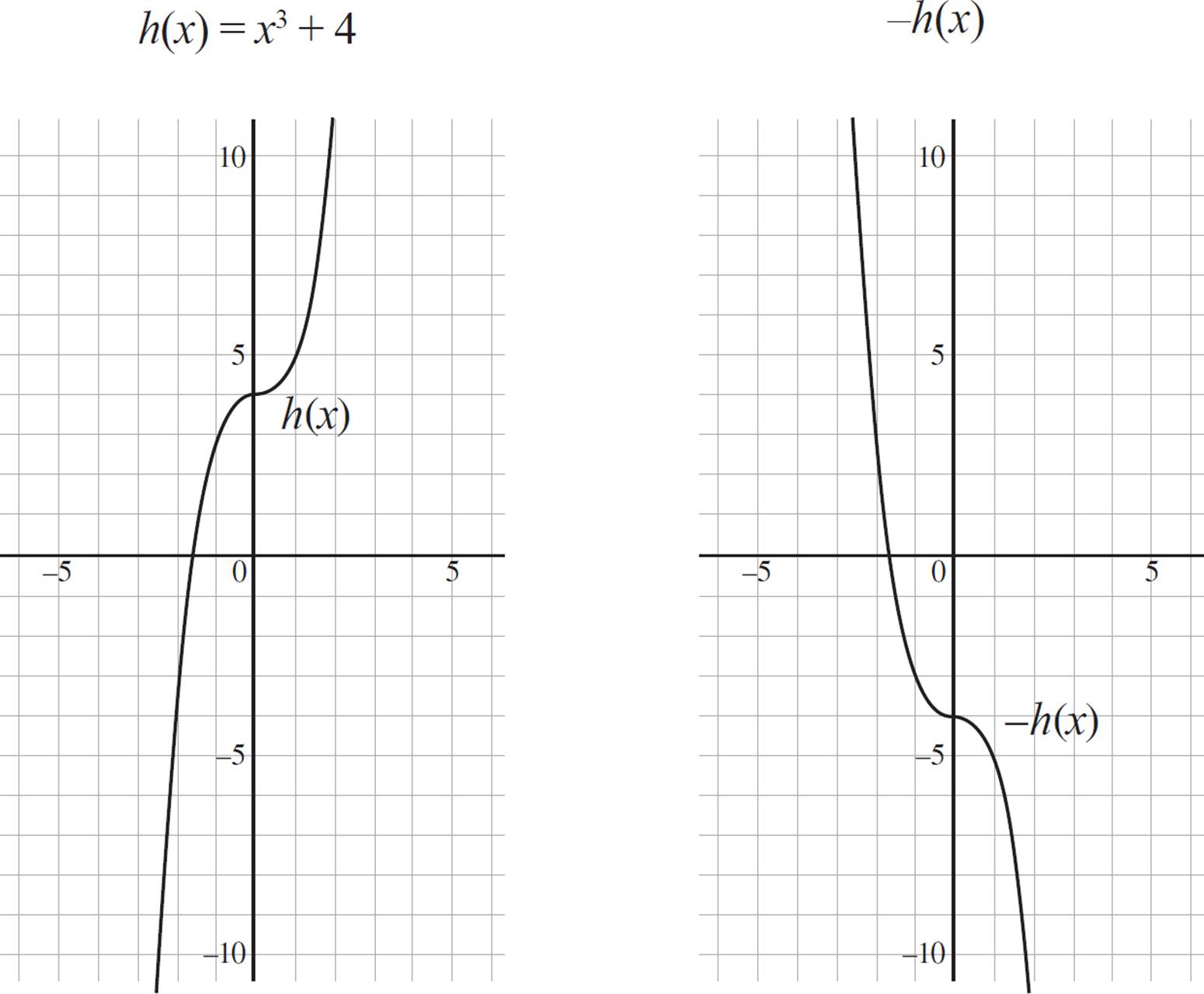
You can also reflect a function over the y-axis. Take a look at the function h(x) = x3 + 4 and its reflection over the y-axis, h(−x):
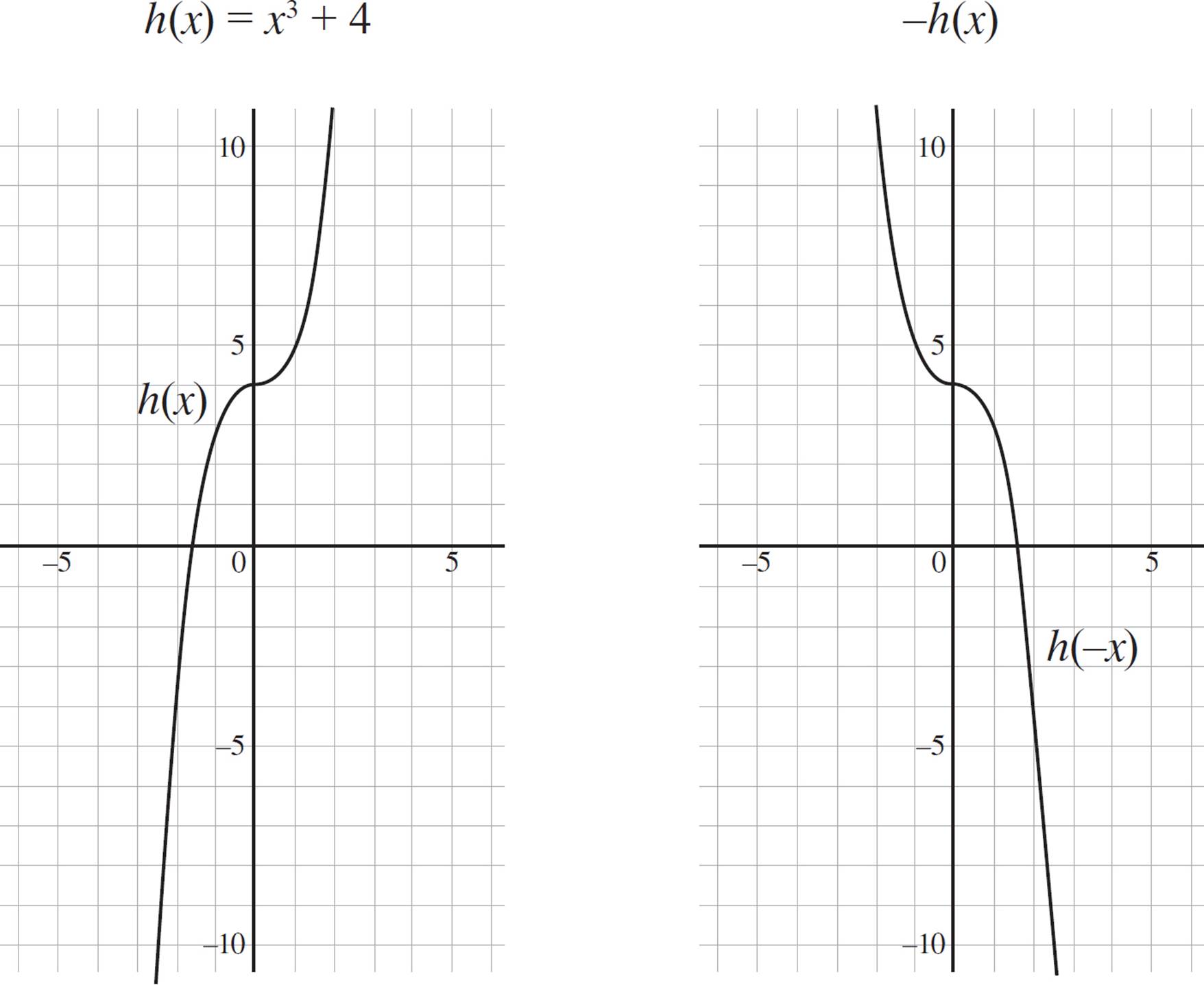
−ƒ(x) reflects ƒ(x) about the x-axis.
ƒ(−x) reflects ƒ(x) about the y-axis.
Now that we’ve covered function reflections, let’s try some questions.
Leave the Negative
Exes Outside
Having some difficulty
remembering when to
reflect a function over
the x- or y-axis? Use
this association: After
a rough breakup, you
may push a negative ex
out of your life. And in
math, if the negative
sign is outside the
function’s argument,
the graph is reflected
about the x-axis.
EXAMPLE 
If p(x) = x2 − 3, is the graph p(−x) + 1 reflected about the x- or y-axis? Graph both p(x) and p(−x) + 1 in the coordinate plane.
There are three parts to this question: (1) determining whether p(−x) + 1 is a reflection of p(x) about the x- or y-axis, (2) graphing p(x), and (3) graphing p(−x) + 1, a transformation that involves a reflection and shift of p(x). First figure out whether p(−x) + 1 is a reflection of p(x) across the x- or y-axis. When any function ƒ(x) is transformed as ƒ(−x), the graph is reflected about the y-axis.
Next, graph the original function, p(x) = x2 − 3. Note that p(x) is simply a transformation of the most basic quadratic, p(x) = x2. Here, −3 is not associated with the x-term, so simply shift the vertex of the graph of x2 down three units from the origin. Refer to the graph below.
Finally, graph p(−x) + 1, a transformation of p(x) that involves a reflection across the y-axis and a shift. If you were asked to reflect p(x) as p(−x), the two reflections would be identical. However, you are asked to graph p(−x) + 1. Since the positive 1 is not associated with the x-term, you will shift the graph of p(−x) up one unit on the y-axis. The resulting graphs of p(x), shown as a solid line, and p(−x) + 1, shown as a dashed line, are as follows:
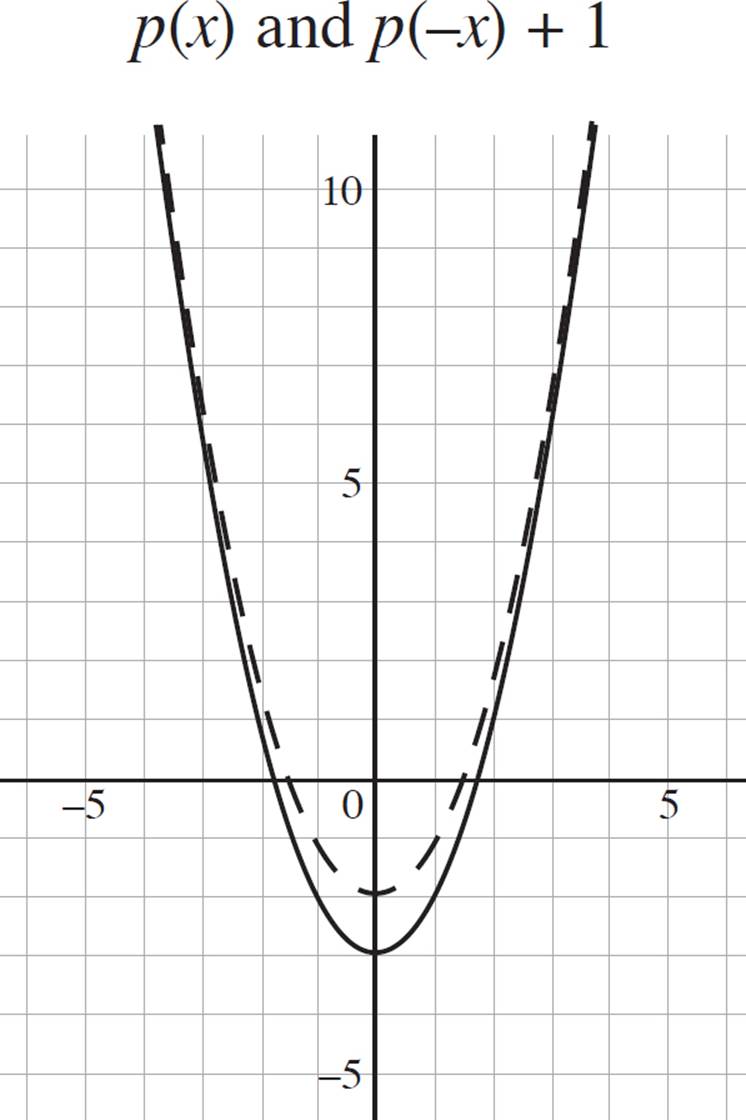

Let’s try one more question before we move on.
EXAMPLE 
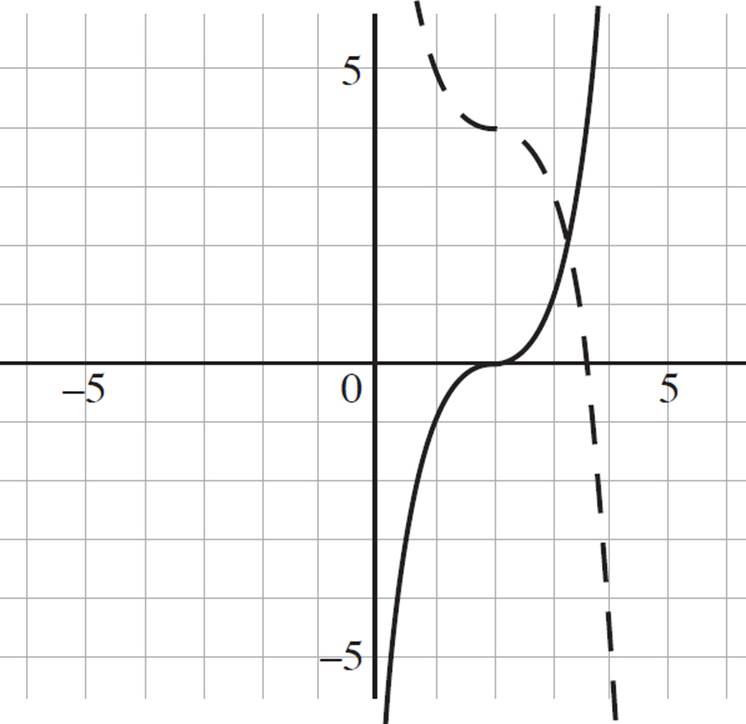
The graph above shows the function j(x) = (x − 2)3 as a solid line and the function k(x) as a dashed line. Which of the following could be the equation for k(x) ?
A) k(x) = −(x − 2)3
B) k(x) = −(x + 2)3
C) k(x) = (−x + 2)3 + 4
D) k(x) = (−x + 2)3 − 4
This question requires you to identify the equation of k(x), represented by the dashed line in the provided graph, given that j(x) = (x − 2)3. Tackle each answer choice one at a time. In (A), k(x) = −(x − 2)3, k(x) is equal to −j(x), which means that k(x) is the graph of j(x) reflected about the y-axis. (Remember that when any function ƒ(x) is transformed as ƒ(−x), the graph is reflected about the y-axis.) In the graph provided, however, the function j(x) is not reflected across the y-axis to produce k(x); eliminate (A). Similarly, (B) represents a reflection of j(x) across the y-axis and, therefore, can be eliminated.
Now, you are left with (C) and (D), which are functions that have both a reflection and a shift. In fact, the only difference between the functions is the shift up or down by four units. In the graph provided, the zero of function k(x), where x = 2, is four units higher than that of j(x), indicating an upward shift. Since (D), k(x) = (−x + 2)3 − 4, indicates that the graph is shifted down by four units, it can be eliminated. In turn, the function k(x) in the provided graph is represented by the equation k(x) = (−x + 2)3 + 4, so the answer is (C).
The following graphs show the functions in (A), (B), and (D), where k(x) is represented as a dashed line, and the reflection of k(x) is shown as a solid line:
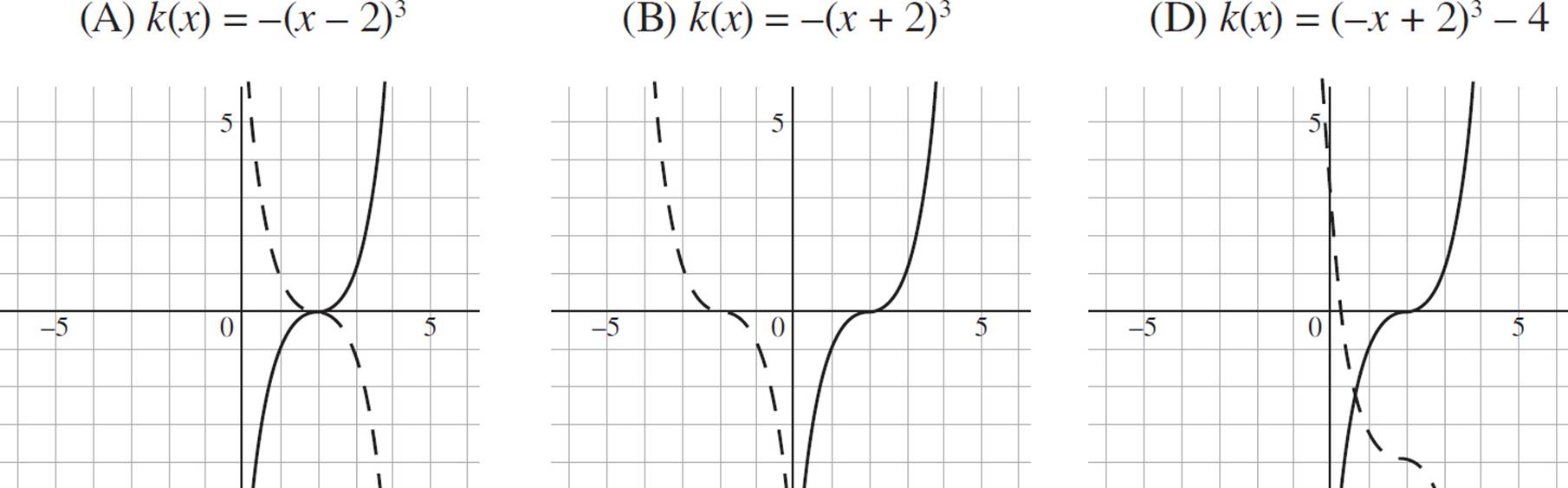


Here is how you may see translations and reflections on the SAT.
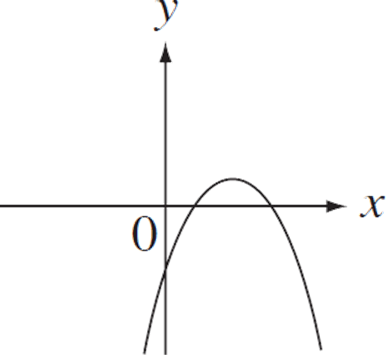
The graph of y = g(x) is shown in the figure above. If g(x) = ax2 + bx + c for constants a, b, and c, and if abc ¹ 0, then which of the following must be true?
A) ac > 1
B) c > 1
C) ac > 0
D) a > 0