High School Algebra I Unlocked (2016)
Chapter 9. Manipulating Functions
Lesson 9.4. Vertical and Horizontal Scaling
Thus far, we’ve been transforming functions in a way that preserves the size of the image. Now we’re going to discuss scaling, a transformation that alters the relative size of an image by stretching or compressing the figure.
You can resize transformations by changing the value of a in a function. When the value of a > 1, the image will have a vertical stretch in the y-direction, appearing taller and thinner than the pre-image. Conversely, if 0 < a < 1, the image will have a vertical compression in the y-direction, appearing shorter and wider than the pre-image. In essence, the value of a determines the stretching or shrinking of an image. Take a look at how this works in the following graphs:
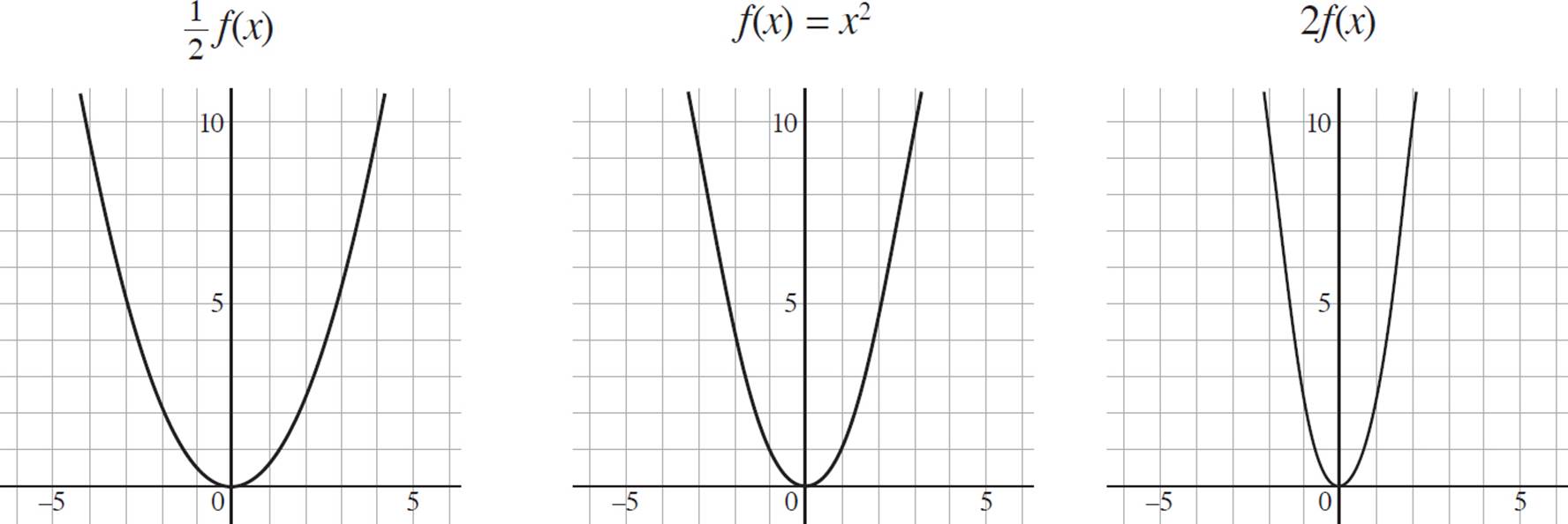
You can also stretch or compress the scale of an image by changing the value of b within the argument of any function ƒ(bx) = y. If b > 1, the image will have a horizontal compression in the x-direction, appearing taller and thinner than the original function. On the other hand, if 0 < b < 1, the image will have a horizontal stretch in the x-direction, appearing shorter and wider than the pre-image.
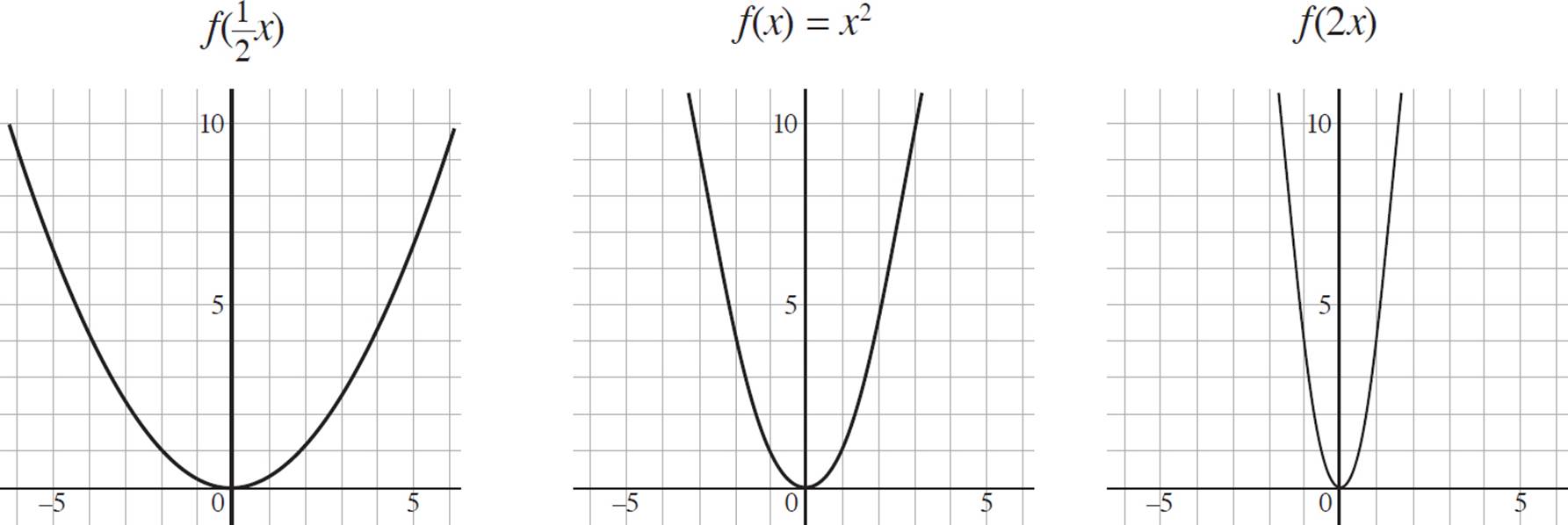
Unlike vertical and horizontal translations, which can occur simultaneously, a function cannot exhibit a horizontal stretch and a vertical compression simultaneously. (It would just be too much. The world of math can’t handle it.)
Now let’s try out some questions that deal with horizontal and vertical stretching and compressing of functions.

Whenever you are working with translation questions that deal with quadratics, think about how the given function is different from f(x) = x2. Here, you are given a graph of a parabola that is opening downwards, and is shifted to the right and upwards. First, plug in some numbers to create the function g(x) and determine the values of a, b, and c. For example, based on the graph, we could say that g(x) = −(x − 2)2 + 1, which is a function that opens downwards and shifted up and to the right of the origin. Expand out the function to find the following:
g(x) = −(x − 2)2 + 1
g(x) = −(x2 − 4x + 4) + 1
g(x) = −x2 + 4x − 4 + 1
g(x) = −x2 + 4x − 3
Now that the function is in standard form, we can see that the values of a and c are negative; eliminate both (B) and (D).
Now determine if ac > 1 or ac > 0. Plug in fractional values like x = 1/2 and x = 3/4 for the x-intercepts of the parabola, expand out the terms, and determine the value of ac.
g(x) = −(x − 1/2)(x − 3/4)
g(x) = −(x2 − 1/2x − 3/4x + 3/8)
g(x) = −x2 + 5/4x − 3/8
Once again, the function g(x) is in standard form, and we can see that a = −1 and c = −3/8. Thus, the value of ac = 3/8, ac > 0, and the correct answer is (C).
EXAMPLE 
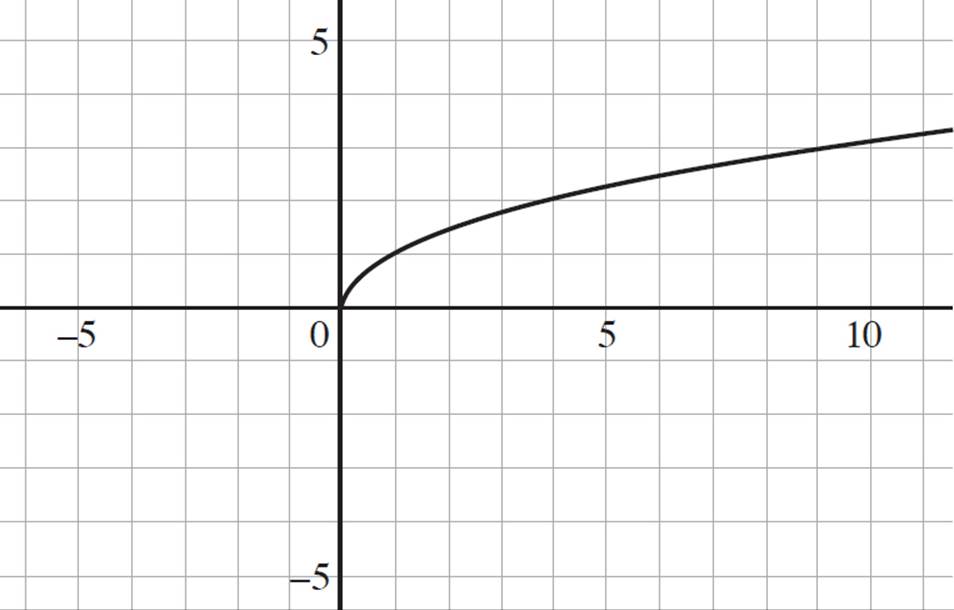
The graph above shows the function g(x) = ![]() . Which of the following graphs depicts the function g(−5x) ?
. Which of the following graphs depicts the function g(−5x) ?
A) 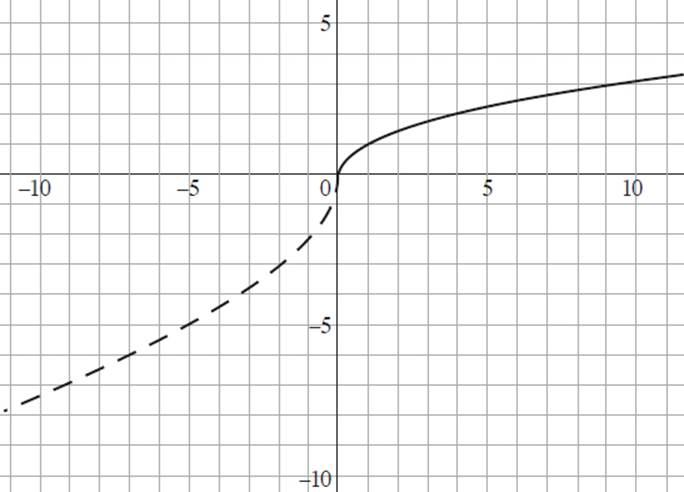
B) 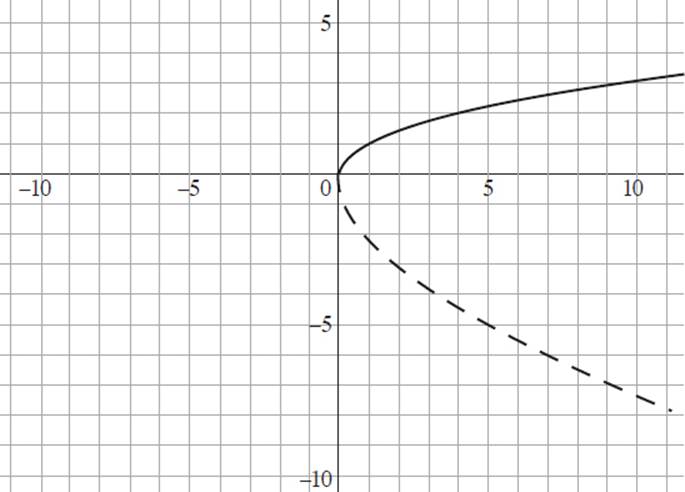
C) 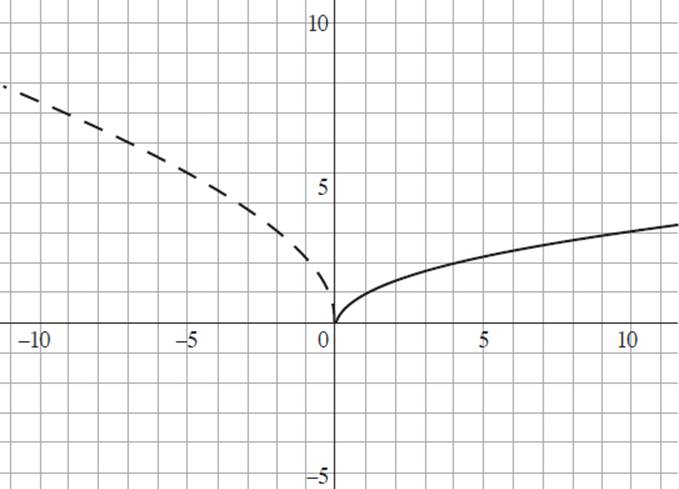
D) 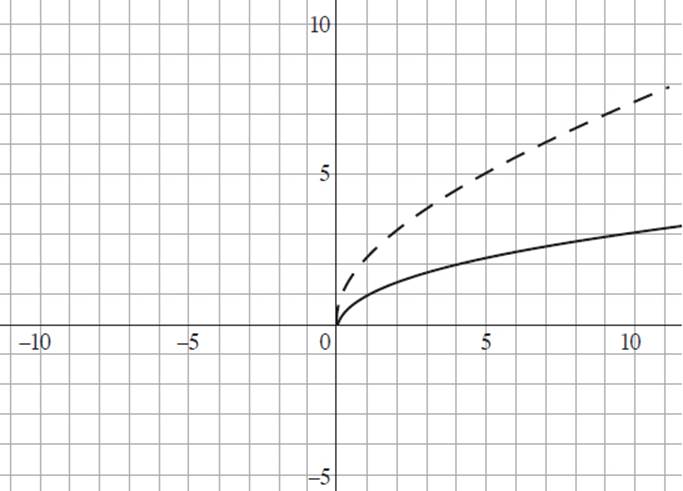
If you’re wondering
why the graph of ![]()
exists only in the
first quadrant, recall
that the square
root of a number is
always positive; e.g.,![]() = 2,
= 2, ![]() = 4, and
= 4, and![]() = 10. Since
= 10. Since
the first quadrant
is the only one in
which all the x- and
y-values are positive,
the representation
of ![]() is limited to
is limited to
the first quadrant.
Now here’s a graph that we haven’t looked at before! This question provides the graph of the function g(x) = ![]() and requires you to identify the graph of g(−5x). While the graph of
and requires you to identify the graph of g(−5x). While the graph of ![]() may look a bit odd, no need to be intimidated; square roots must be positive, which is why the graph is present only in first quadrant of the coordinate plane.
may look a bit odd, no need to be intimidated; square roots must be positive, which is why the graph is present only in first quadrant of the coordinate plane.
First, look at how the function g(x) is transformed: −5 is placed into the argument of the function g(x). Thus, there are two things happening here: we are introducing a negative sign into the argument of the function, and we are changing the scale of the function.
Based on our earlier discussion, we know that if the value of b is negative in a general function ƒ(bx) = y, the image will be reflected about the y-axis. Therefore, you can eliminate (B), which is a graph of −g(5x), and (D), which is the graph of g(5x), as neither image depicts a reflection about the y-axis. You can also eliminate (A), which is the graph of −g(−5x), as the pre-image is reflected over both the x- and y-axes.
But what if you didn’t notice that? Well, consider the value of 5 placed inside the argument of g(x). Given a function ƒ(bx) = y, when b > 1, the image will be compressed horizontally along the x-axis, appearing taller than the original function. The only image that shows a pre-image that has been reflected about the y-axis and horizontally compressed is (C).

Fantastic! You now know how to manipulate functions in all sorts of ways. Again, if you understand how a, b, c, and d affect a function, you will have a much easier time working through tricky function questions. Remember:
aƒ (b(x + c)) + d
• a affects vertical stretching and shrinking, and up-down orientation.
○ |a| > 1 stretches image
○ |a| < 1 shrinks image
○ If a is negative, the graph is reflected about the x-axis.
• b affects horizontal stretching and shrinking.
○ |b| > 1 shrinks image
○ |b| < 1 stretches image
○ If b is negative, the graph is reflected about the y-axis.
• c affects horizontal shifts.
○ c > 0 shifts image to the left
○ c < 0 shifts image to the right
• d affects vertical shifts.
○ d > 0 shifts image upward
○ d < 0 shifts image downward
DRILL
CHAPTER 9 PRACTICE QUESTIONS
Click here to download a PDF of Chapter 9 Practice Questions.
Directions: Complete the following problems as specified by each question. For extra practice, try using an alternative method to solve the problem or check your work.
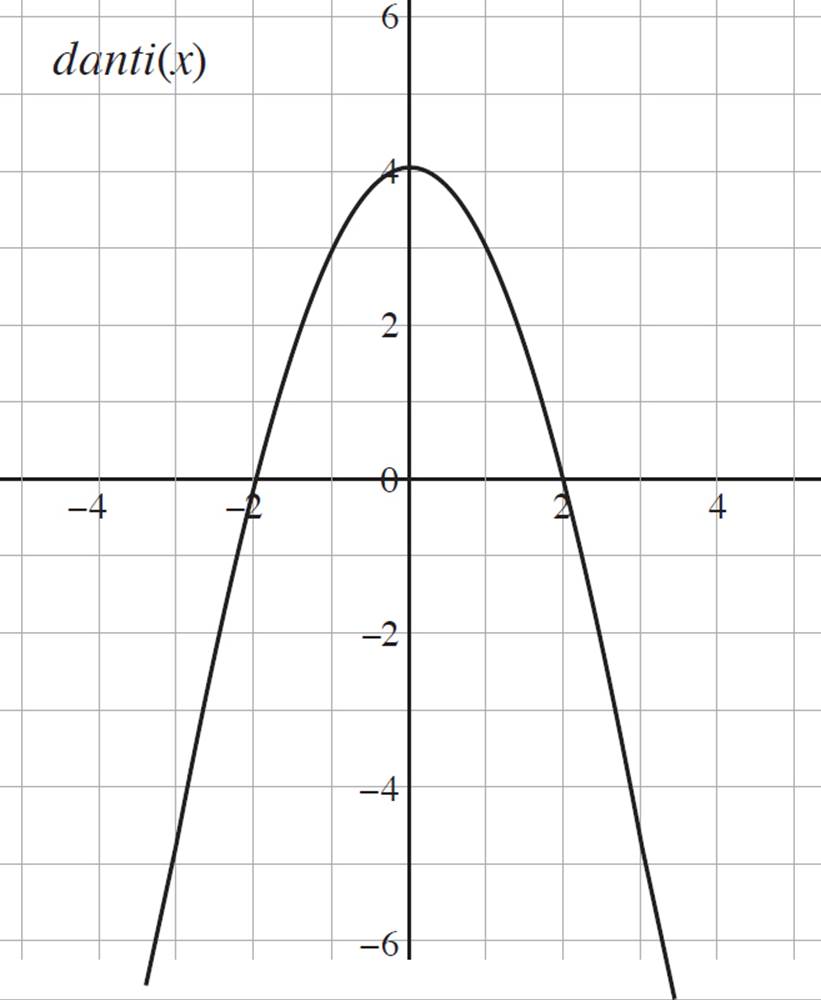
1. Given the following graph of danti(x), define the function.
2. Graph the function h(x) = (x − 2)2 + 4 in the coordinate plane.
Questions 3−5 refer to the function z(x) = (2x − 3)2 − 1.
3. Graph the function z(x) = (2x − 3)2 − 1 in the coordinate plane.
4. Graph the function −z(x) in the coordinate plane.
5. Determine algebraically whether the function z(x) is even, odd, or neither.
6. Determine algebraically whether the function molly(x) = 2x3 − x5 is even, odd, or neither.
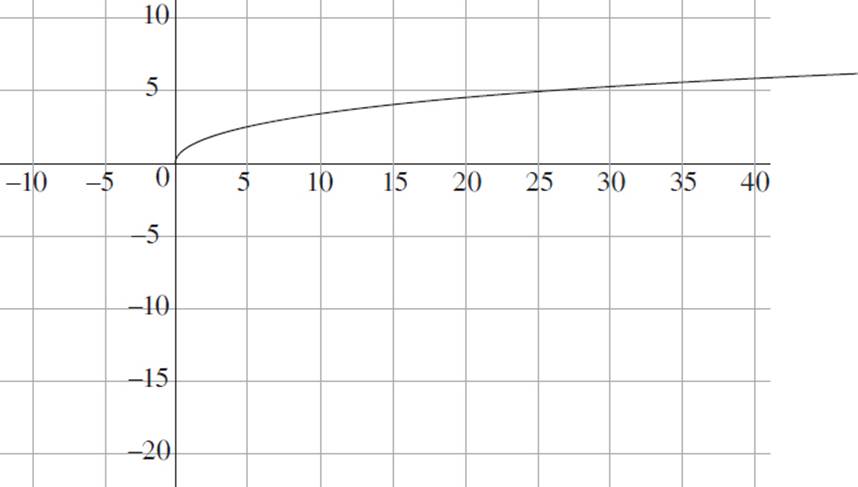
7. Given the following graph of s(x) = ![]() , graph −s(2x).
, graph −s(2x).
Questions 8−9 refer to the functions pop(x) = −(![]() x + 8)2 −
x + 8)2 − ![]() and corn(x) = x2.
and corn(x) = x2.
8. If pop(x) = − (![]() x + 8)2 −
x + 8)2 − ![]() is a transformation of corn(x) = x2, all of the following are true regarding pop(x) EXCEPT
is a transformation of corn(x) = x2, all of the following are true regarding pop(x) EXCEPT
A) pop(x) is shifted down the y-axis by ![]() of a unit.
of a unit.
B) pop(x) is reflected about the x-axis.
C) pop(x) has a horizontal stretch.
D) pop(x) is shifted to the right by 8 units.
9. Which of the following graphs represents pop(x) and corn(x) in the coordinate plane?
(Note: corn(x) is represented with a solid line, and pop(x) is represented with a dashed line.)
A) 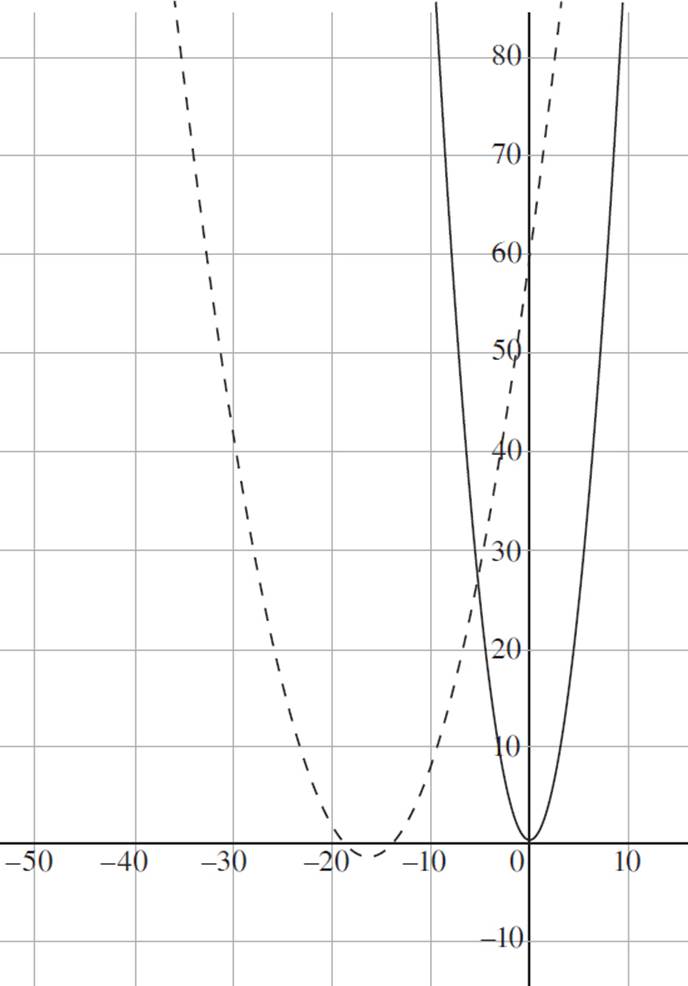
B) 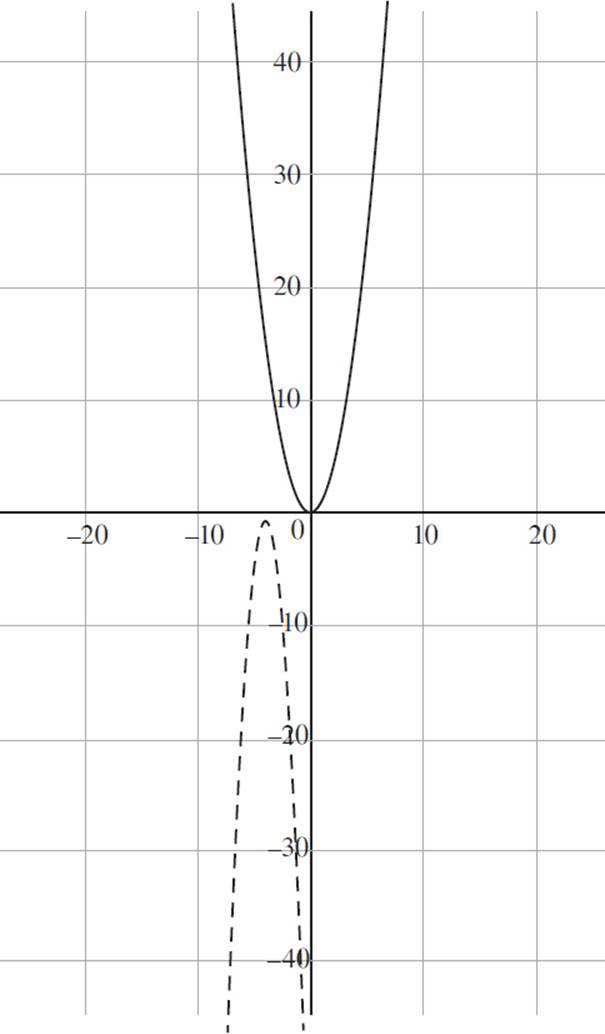
C) 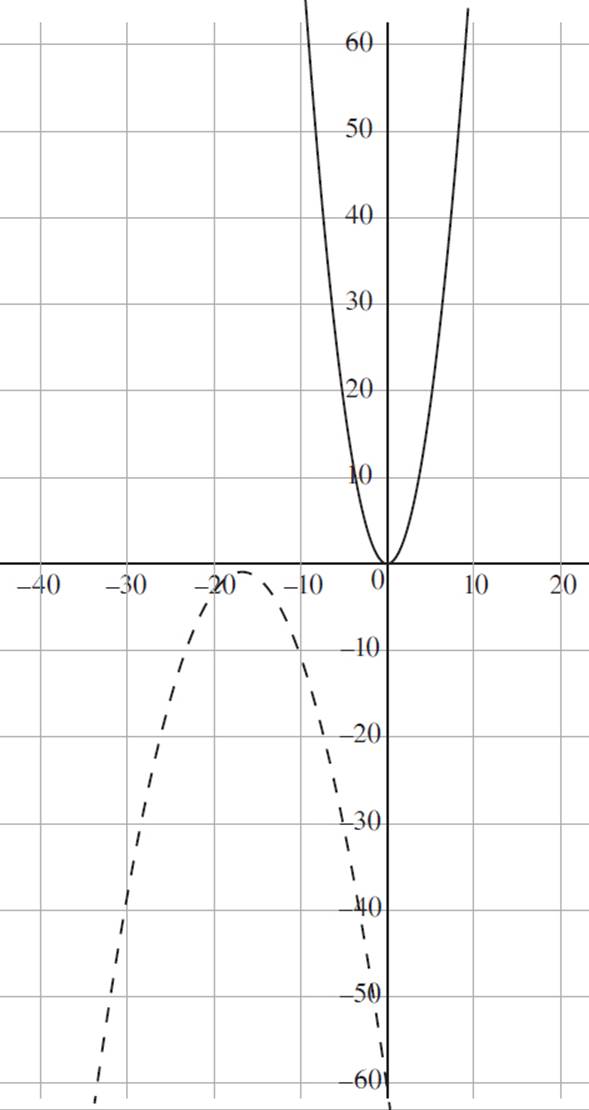
D) 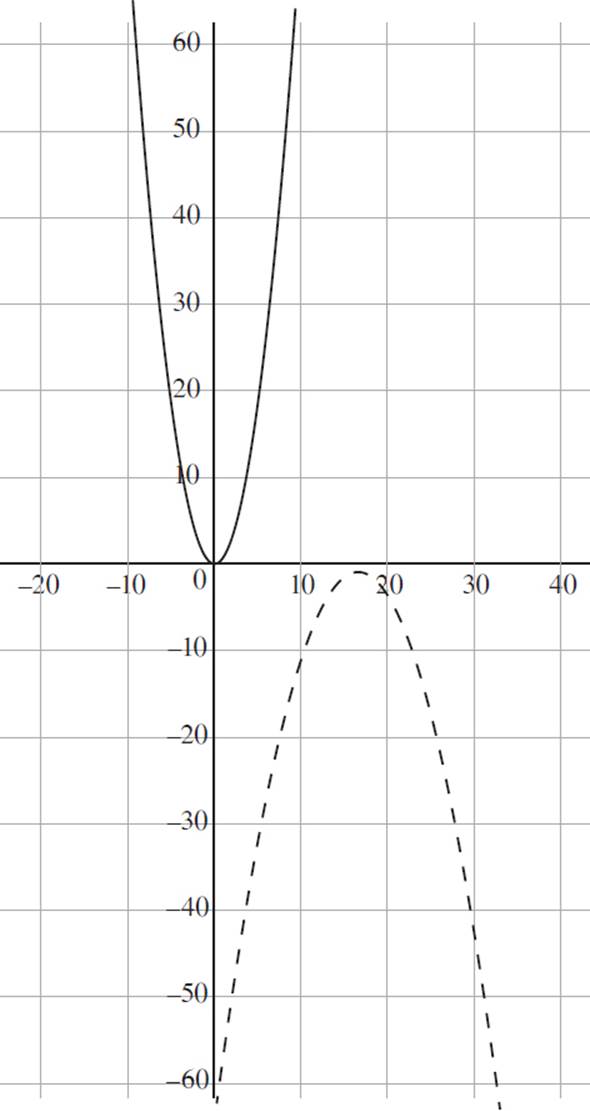
SOLUTIONS TO CHAPTER 9 PRACTICE QUESTIONS
1. danti(x) = −x2 + 4
This question requires you to define danti(x), given the graph. Whenever you see a quadratic graphed, remember that it is a transformation of the function ƒ(x) = x2. Now you just need to determine how the graph of danti(x) = x2 is transformed. First, deal with the vertical shift in the graph. Given the function ƒ(x) = x2 + k, the function shifts upwards by k units if k > 0, and the function shifts downwards by k units if k < 0. Since the graph is shifted upwards by 4 units, danti(x) = x2 + 4. Next, consider the fact that the parabola opens downwards, which indicates that that the value of a in the current quadratic, danti(x) = ax2 + 4, is negative. Thus, danti(x) = −x2 + 4.
2. Here, you need to graph the function h(x) = (x − 2)2 + 4. First, recall that every quadratic is a transformation of the function ƒ(x) = x2, and then tackle the horizontal shift. Given the function ƒ(x) = (x + h)2 + 4, the function shifts to the left by h units if h > 0, and the function shifts to the right by h units if h < 0. Since h = −2, the function h(x) is shifted to the right by 2 units.
Now deal with the vertical shift in the graph. Given the function, ƒ(x) = (x − 2)2 + k, the function shifts upwards by k units if k > 0, and the function shifts downwards by k units if k < 0. Therefore, the function h(x) is shifted upwards by 4 units.
Then you need to identify the roots of the quadratic by setting h(x) = 0 and solving for x. Thus, (x − 2)2 + 4 = 0, (x − 2)2 = −4, x − 2 = ±![]() , and x = 2 ±
, and x = 2 ±![]() . Since you have to take the square root of a negative number, you know that the function has no real solutions and, therefore, has no x-intercepts.
. Since you have to take the square root of a negative number, you know that the function has no real solutions and, therefore, has no x-intercepts.
Finally, identify the y-intercept of the function by setting x = 0 and solving for y, or h(x): h(x) = (x − 2)2 + 4, h(x) = (0 − 2)2 + 4, h(x) = 4 + 4, h(x) = 8, and the y-intercept is (0, 8). The end result is a transformation of the function ƒ(x) = x2, where ƒ(x) is shifted to the right by 2 units, shifted up 4 units, has a vertex at (2, 4), and a y-intercept of (0, 8). Your graph should look like the following:
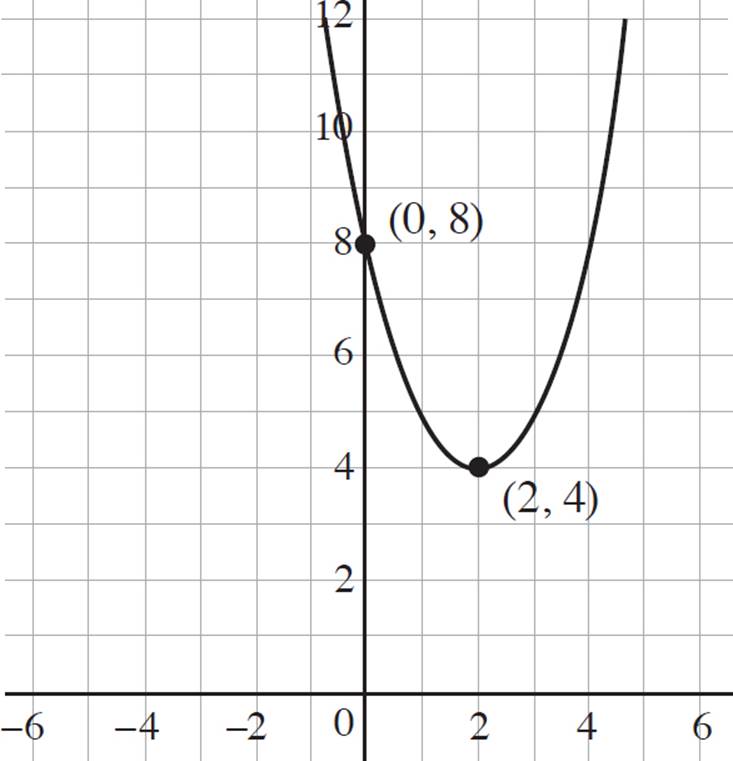
3. This question asks you to graph the function z(x) = (2x − 3)2 − 1 in the coordinate plane. First, identify the vertex of the function. Since the vertex form of a function is ƒ(x) = (x − h)2 + k, where the vertex is (h, k), you know the vertex of z(x) = (2x − 3)2 − 1 is (![]() , −1). Now tackle the transformations, recalling that every quadratic is a transformation of the function ƒ(x) = x2.
, −1). Now tackle the transformations, recalling that every quadratic is a transformation of the function ƒ(x) = x2.
Start by finding the horizontal shift. Given ƒ(x) = (x + h)2 + 4, the function shifts to the left by h units if h > 0, and the function shifts to the right by h units if h < 0. If we rewrite the function z(x) in vertex form, where ƒ(x) = a(x + h)2 − k, we get z(x) = (2x + (− 3))2 − 1. Therefore, h = −3/2, and the function ƒ(x) is shifted to the right by 1.5 units.
Now deal with the vertical shift in the graph. Given ƒ(x) = (2x − 3)2 + k, the function shifts upwards by k units if k > 0, and the function shifts downwards by k units if k < 0. Thus, since k = −1, the function z(x) is shifted downwards by 1 unit.
Furthermore, you know that in a function ƒ(x) = (ax − h)2 + k, the function will have a vertical stretch in the y-direction when a > 1. Since a = 2 in the function z(x), you know that the final image will be taller and thinner than the basic quadratic function, ƒ(x) = x2.
Now you need to identify the roots of the quadratic by setting z(x) = 0 and solving for x:
(2x − 3)2 − 1 = 0
(2x − 3)2 = 1
2x − 3 = ±![]()
2x = 3 ± 1, x = 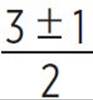
x = 1 and x = 2
Thus, the roots of the solution occur at (1, 0) and (2, 0).
Next, identify the y-intercept of the function by setting x = 0 and solving for y, or z(x):
z(x) = (2x − 3)2 − 1
z(x) = (2(0) − 3)2 − 1
z(x) = (−3)2 − 1
z(x) = 9 − 1
z(x) = 8
Thus, the y-intercept is (0, 8).
Finally, graph the function to find a transformation of the function ƒ(x) = x2, where ƒ(x) is compressed, shifted to the right by 3 units, shifted down 1 unit, has a vertex at (![]() , −1), roots of (1, 0) and (2, 0), and a y-intercept of (0, 8). Your graph should look like this:
, −1), roots of (1, 0) and (2, 0), and a y-intercept of (0, 8). Your graph should look like this:
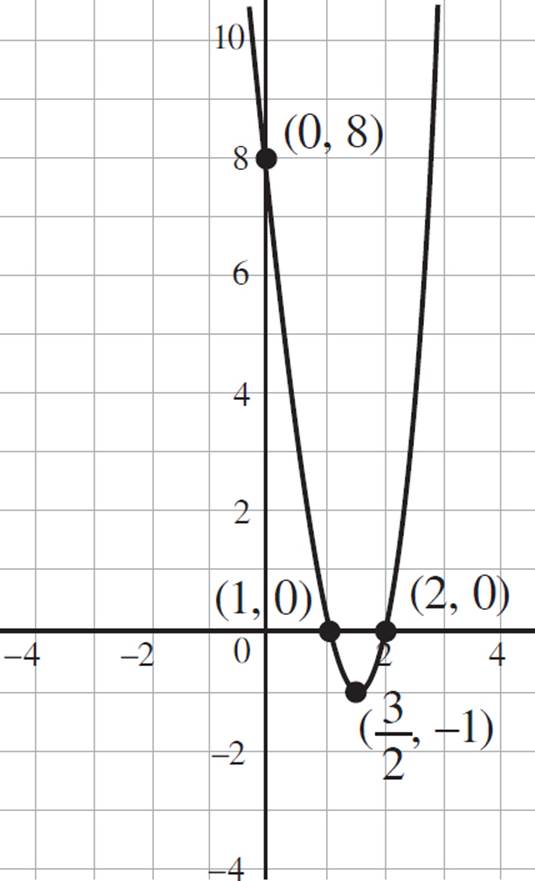
4. Now that you’ve graphed z(x) in the coordinate plane, you have to graph −z(x). When dealing with a negative sign inside or outside the argument of the function, you are dealing with reflections, which cause you to flip the original graph over the x- or y-axis. Given a function ƒ(x), −ƒ(x) reflects ƒ(x) over the x-axis, and ƒ(−x) reflects ƒ(x) over the y-axis. Since you are given the function z(x) and asked to graph −z(x), you will reflect the function over the x-axis, maintaining the roots of (1, 0) and (2, 0), but changing they-intercept to (0, −8) and the vertex to (3/2, 1). The reflection graph should appear as the dashed line in the following graph.
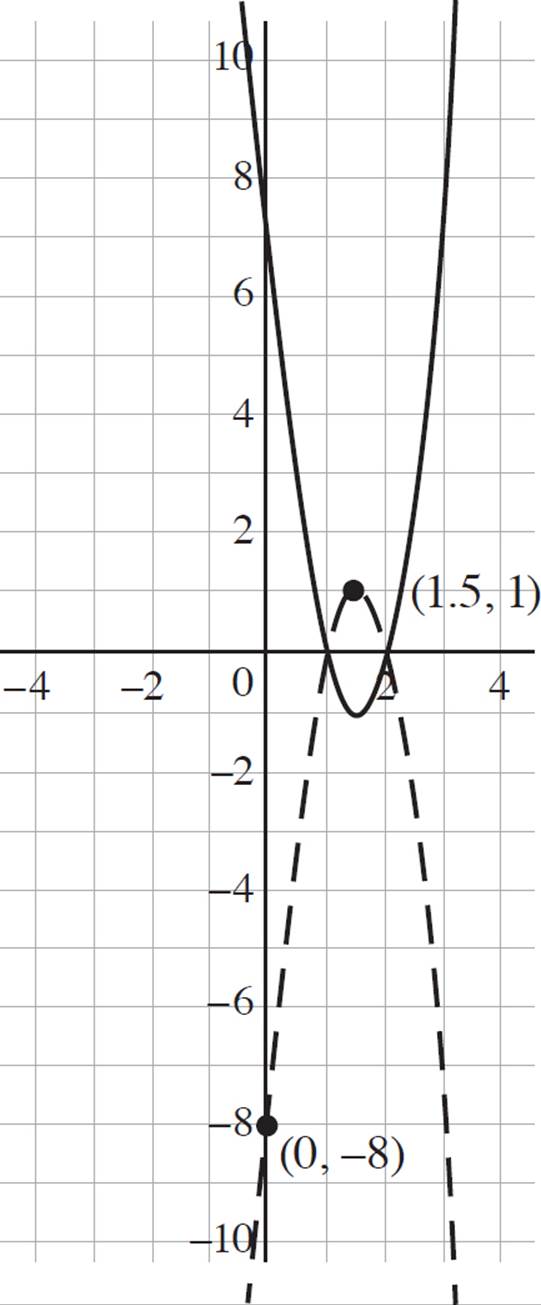
5. Neither even nor odd
This question requires you to determine algebraically whether the function z(x) is even, odd, or neither. Plug in −x to the function z(x) = (2x − 3)2 − 1, and then simplify:
z(x) = (2x − 3)2 − 1
z(−x) = (2(−x) − 3)2 − 1
z(−x) = (−2x − 3)2 − 1
z(−x) = (−2x − 3)(−2x − 3) − 1
z(−x) = 4x2 + 6x + 6x + 9 − 1
z(−x) = 4x2 + 12x + 8
z(−x) = (2x + 3)2 − 1
In this scenario, ƒ(x) ≠ ƒ(−x) and ƒ(−x) ≠ −ƒ(x), so the function is neither even or odd.
6. Odd
Here, you are required to determine if the function molly(x) = 2x3 − x5 is even, odd, or neither. Plug in −x to the function molly(x) = 2x3 − x5 and simplify:
molly(x) = 2x3 − x5
molly(−x) = 2(−x)3 − (−x)5
molly(−x) = −2x3 + x5
Since the function molly(−x) is the exact opposite of the original function, molly(x), ƒ(−x) = −ƒ(x). Therefore, the function molly(x) is odd.
7. In this question, you are given the graph of s(x) = ![]() and asked to graph −s(2x). Take a look at how the function s(x) is being transformed. First, a negative sign is applied to the entire argument of the function s(x), indicating that the new function is a reflection of the original function. Since a reflection is a graph that results from flipping the original graph over the x- or y-axis, where −ƒ(x) reflects ƒ(x) over the x-axis, and ƒ(−x) reflects ƒ(x) over the y-axis, −s(2x) is reflected across the x-axis. Next, consider the value of 2 placed inside the argument of −s(2x). Given a function ƒ(bx) = y, when b > 1, the image will be compressed horizontally along the x-axis.
and asked to graph −s(2x). Take a look at how the function s(x) is being transformed. First, a negative sign is applied to the entire argument of the function s(x), indicating that the new function is a reflection of the original function. Since a reflection is a graph that results from flipping the original graph over the x- or y-axis, where −ƒ(x) reflects ƒ(x) over the x-axis, and ƒ(−x) reflects ƒ(x) over the y-axis, −s(2x) is reflected across the x-axis. Next, consider the value of 2 placed inside the argument of −s(2x). Given a function ƒ(bx) = y, when b > 1, the image will be compressed horizontally along the x-axis.
Finally, before you graph the function, identify a few points that lie on the graph of −s(2x) = −![]() . If you set x = 2, you will find that
. If you set x = 2, you will find that
−s(2x) = −![]()
= −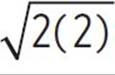
= −![]()
= −2
Therefore, the point (2, −2) lies on the function −s(2x). If you set x = 8, you will find that
−s(2x) = −![]()
= −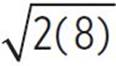
= −![]()
= −4
Thus, the point (8, −4) lies on the function −s(2x). If you set x = 32, you will find that
−s(2x) = −![]()
= −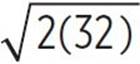
= −![]()
= −8
Therefore, the point (32, −8) lies on the function −s(2x).
Finally, you can graph the function −s(2x), transforming s(x) by reflecting the function across the x-axis, horizontally compressing the function, and ensuring that the function passes through the points (2, −2), (8, −4), and (32, −8). The graph of −s(2x), shown as a dashed line, is as follows.
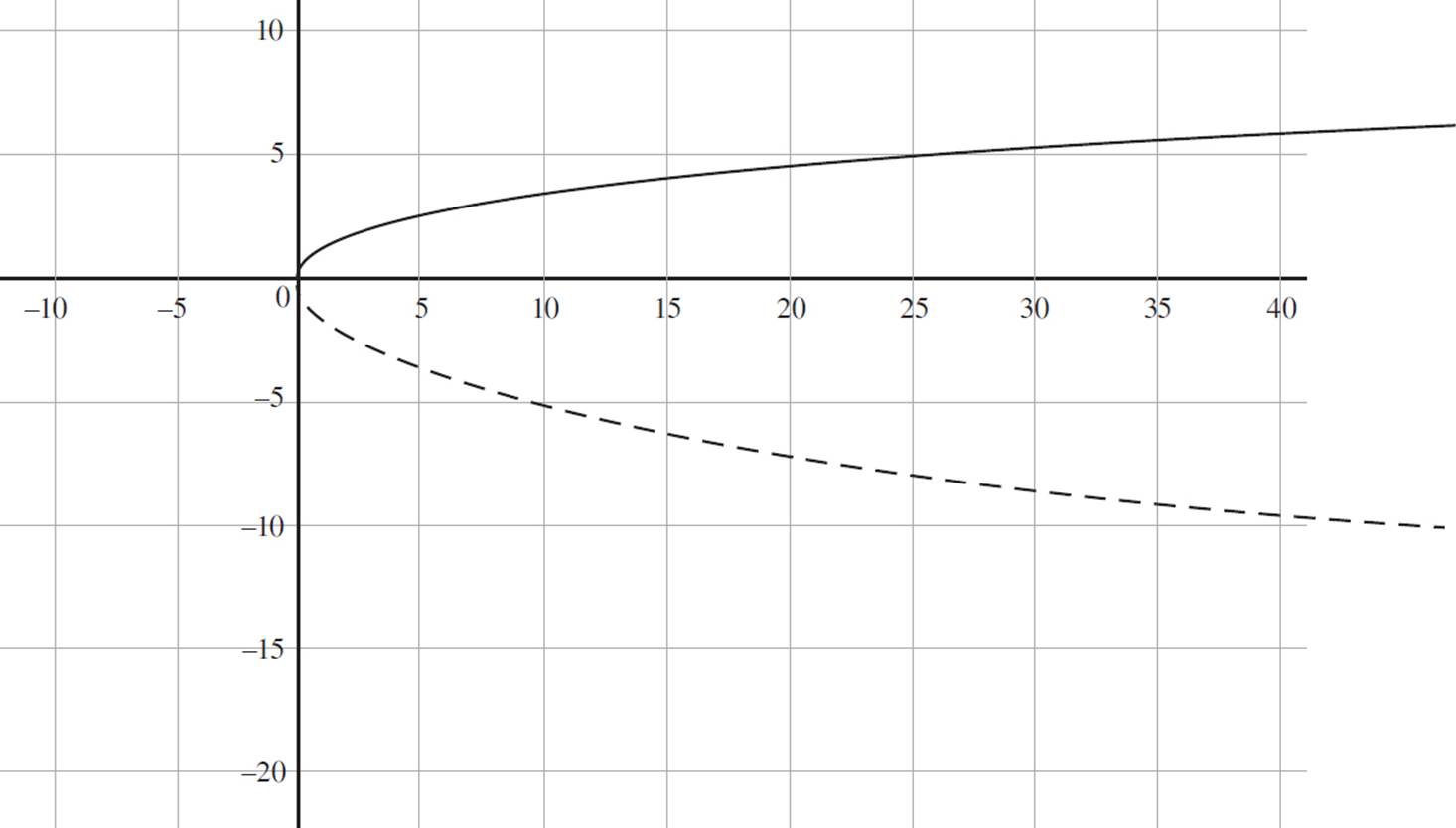
8. D
This question deals with the theory behind the math. You are told that pop(x) = −(1/2x + 8)2 − 3/4 is a transformation of corn(x) = x2, and you need to determine which given statement is false. So, tackle each statement in turn and eliminate the statements that are true.
Choice (A) states that pop(x) is shifted down the y-axis by 3/4 of a unit. Given the function pop(x) = −(1/2x + 8)2 + k, the function shifts upwards by k units if k > 0, and the function shifts downwards by k units if k < 0. Since k = −3/4, the function pop(x) is shifted downwards by 3/4 of a unit; this is true, so eliminate (A).
Choice (B) states that pop(x) is reflected across the x-axis. A reflection is a graph that results from flipping the original graph over the x- or y-axis, where −ƒ(x) reflects ƒ(x) over the x-axis, and ƒ(−x) reflects ƒ(x) over the y-axis. Since the negative sign is not applied to the argument, the function is reflected about the x-axis; therefore, (B) is also true and you can eliminate it.
Choice (C) states that pop(x) has a horizontal stretch. Given a function ƒ(bx) = y, if b > 1, the image will have a horizontal compression in the x-direction, appearing taller and thinner than the original function, while the image will have a horizontal stretch in the x-direction, appearing shorter and wider than the original function if 0 < b < 1. Since the value of b = 1/2 in pop(x), the function will have a horizontal stretch. Choice (C) is true and thus not the answer.
Finally, consider (D), which states that pop(x) is shifted to the right by 8 units. Given the function pop(x) = −(1/2x − h)2 − 3/4, the function shifts to the left by h units if h > 0, and the function shifts to the right by h units if h < 0. Since h = 16, the function pop(x) is shifted to the left by 16 units. Therefore, the only statement that is false is (D), which is the correct answer.
9. C
This question expands upon the previous question: you need to identify the graphs of pop(x) and corn(x) in the coordinate plane. You’re told that pop(x) = −(1/2x + 8)2 − 3/4 is a transformation of corn(x) = x2. Given a function ƒ(bx) = y, if b > 1, the image will have a horizontal compression in the x-direction, appearing taller and thinner than the original function, while the image will have a horizontal stretch in the x-direction, appearing shorter and wider than the original function if 0 < b < 1. Since the value of b = 1/2 inpop(x), the function will have a horizontal stretch; eliminate (B), as this graph shows a horizontal compression. Now, consider whether pop is reflected about the x-axis. Again, a reflection is a graph that results from flipping the original graph over the x- or y-axis, where −ƒ(x) reflects ƒ(x) about the x-axis, and ƒ(−x) reflects ƒ(x) about the y-axis. Since the negative sign is not applied to the argument, the function is reflected about the x-axis, and (A) can be eliminated. Given the function pop(x) = −(1/2x + h)2 − 3/4, the function shifts to the left by h units if h > 0, and the function shifts to the right by h units if h < 0. Since h = 16, the function pop(x) is shifted to the left by 16 units, and (D) can be eliminated. Thus, the graph that accurately represents the functions pop(x) andcorn(x) is (C).
REFLECT
Congratulations on completing Chapter 9!
Here’s what we just covered.
Rate your confidence in your ability to:
•Identify types of transformations
1 2 3 4 5
•Perform vertical and horizontal translations
1 2 3 4 5
•Determine whether a function is even or odd
1 2 3 4 5
•Explain and perform the processes for reflecting, stretching, and compressing functions
1 2 3 4 5
If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.
CHAPTER 9 KEY POINTS
![]() A transformation is simply the result of changing the shape or scale of a point, line, or shape. The original figure is known as the pre-image, and the transformed image as the image.
A transformation is simply the result of changing the shape or scale of a point, line, or shape. The original figure is known as the pre-image, and the transformed image as the image.
![]() A function can be transformed through translations, reflections, or scaling.
A function can be transformed through translations, reflections, or scaling.
○ A horizontal or vertical translation changes the location but not the size of figure.
○ A reflection is a mirror image of a figure across either the x- or y-axis.
○ Scaling stretches or compresses the size of the figure.
![]() Shifting the graph up or down is a vertical translation. Shifting the graph left or right is a horizontal translation.
Shifting the graph up or down is a vertical translation. Shifting the graph left or right is a horizontal translation.
![]() Given the function ƒ(x) = x2 + k:
Given the function ƒ(x) = x2 + k:
○ If k > 0, the function shifts upwards by k units.
○ If k < 0, the function shifts downwards by k units.
![]() Given the function ƒ(x) = (x + h)2:
Given the function ƒ(x) = (x + h)2:
○ If h > 0, the function shifts to the left by h units.
○ If h < 0, the function shifts to the right by h units.
![]() A reflection is a graph that results from flipping the original graph over the x- or y-axis: −ƒ(x) reflects ƒ(x) over the x-axis, and ƒ(−x) reflects ƒ(x) over the y-axis.
A reflection is a graph that results from flipping the original graph over the x- or y-axis: −ƒ(x) reflects ƒ(x) over the x-axis, and ƒ(−x) reflects ƒ(x) over the y-axis.
![]() Remember the rules of even and odd functions:
Remember the rules of even and odd functions:
○ For any function ƒ(x), if ƒ(x) = ƒ(−x), the function is even.
○ For any function ƒ(x), if ƒ(−x) = −ƒ(x), the function is odd.
○ For any function ƒ(x), if ƒ(x) ≠ ƒ(−x) and ƒ(−x) ≠ −ƒ(x), the function is neither even or odd.
![]() Changing the value of a in a function a ƒ(x) = y will give either a vertical stretch or compression.
Changing the value of a in a function a ƒ(x) = y will give either a vertical stretch or compression.
○ If the value of a > 1, the graph of your function will give a vertical stretch in the y-direction, appearing taller and thinner than the pre-image.
○ If 0 < a < 1, the image will have a vertical compression in the y-direction, appearing shorter and wider than the pre-image.
![]() Changing the value of b in a function ƒ(bx) = y will give either a horizontal stretch or compression.
Changing the value of b in a function ƒ(bx) = y will give either a horizontal stretch or compression.
○ If the b > 1, the image will have a horizontal compression in the x-direction, appearing taller and thinner than the pre-image.
○ If 0 < b < 1, the image will have a horizontal stretch in the x-direction, appearing shorter and wider than the pre-image.
![]() aƒ(b(x + c)) + d
aƒ(b(x + c)) + d
○ a affects vertical stretching and shrinking, and up-down orientation.
• |a| > 1 stretches image
• |a| < 1 shrinks image
• If a is negative, the graph is reflected across the x-axis.
○ b affects horizontal stretching and shrinking.
• |b| > 1 shrinks image
• |b| < 1 stretches image
• If b is negative, the graph is reflected across the y-axis.
○ c affects horizontal shifts.
• c > 0 shifts image to the left
• c < 0 shifts image to the right
○ d affects vertical shifts.
• d > 0 shifts image upward
• d < 0 shifts image downward