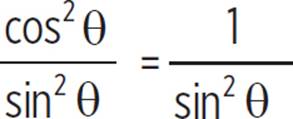High School Algebra II Unlocked (2016)
Chapter 4. Trigonometric Functions
Lesson 4.6. Trigonometric Functions in Real Life
There are many actions that complete some sort of regular cycle periodically and can be modeled by trigonometric functions. For example, the swinging arc of a pendulum provides a relationship of spatial location to time that can be described by a sine or cosine function.

Rebecca is preparing for her trapeze performance. She swings on a trapeze that is connected by 20-foot ropes to its pivot point. She begins her swing from a platform, where the angle of the ropes from the vertical is 2/5 π radians, as shown in the diagram below, and swings to the opposite side and back, repeatedly.
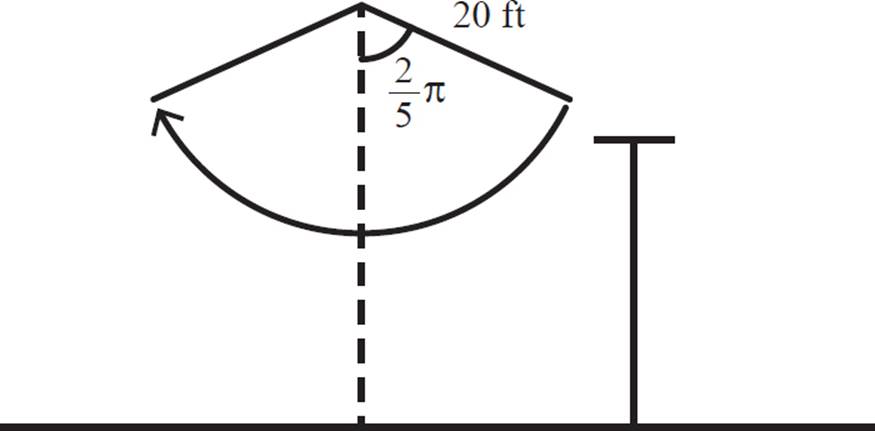
It takes her 8.8 seconds to make one full swing back and forth, returning to her original position.
Let us call the equilibrium position, where Rebecca, on her trapeze, is hanging directly below the pivot point, the zero position. (Note that she only passes through this point during her swings and does not hang stationary there.) This is represented by the point where the arc intersects the vertical dashed line in the diagram. We’ll measure her displacement from this position along the arc she travels, with positive numbers representing locations to the right of the zero position and negative numbers representing locations to the left. The absolute value of her displacement at any time is the distance she is along the arc from the equilibrium position.
(a) Write and graph a trigonometric function that represents Rebecca’s displacement, in feet, from the equilibrium position as a function of time, in seconds.
(b) There is a 20-second musical introduction, at the end of which Rebecca must be at the opposite extreme of her swing from her beginning position. If she wants to swing for as much of the musical introduction as possible, how long should she wait after the music begins to start swinging?
That’s a wordy question! Let’s begin by solving for Rebecca’s displacement measurement at her starting position, which is also the extreme of her swing to the right of the equilibrium position. Remember, θ = s/r, where θ is the central angle measure, s is the arc length subtended by that angle, and r is the radius. For Rebecca’s starting position, when she’s on the platform, θ = 2/5 π and r = 20.
|
2/5 π = s/20 |
Substitute 2/5 π for θ and 20 for r. |
|
8π = s |
Multiply both sides by 20. |
|
s ≈ 25 |
Substitute 3.14 as an approximation for π and multiply by 8. |
Let d represent Rebecca’s displacement from equilibrium, as described above. Her maximum displacement along the arc is 25 feet (d = 25). The extreme point on her swing to the left is also an arc length of 25 feet from the zero position, but we are defining points to the left of center as negative, so d = −25 at the left extreme. Rebecca’s displacement, d, ranges from −25 to 25.
We can assume that
Rebecca’s swing
goes approximately
the same distance
in each direction,
like a pendulum.
We must write a trigonometric function (sine or cosine) that relates Rebecca’s displacement to time. She completes a full cycle (swinging from her beginning position to the opposite extreme and back again to her original position) in 8.8 seconds, so the period of this trigonometric function is 8.8. Her maximum displacement is 25 and her minimum displacement is −25. So, the midline is d = 0, and the amplitude is 25.
Let t represent time, in seconds, since Rebecca started her swing from the platform. At t = 0, d = 25, because she is at her right-side extreme displacement. At t = 8.8, d = 25 again, at the completion of her swing back and forth. Because this is a sine or cosine function, her swing across and her swing back take the same amount of time, so she reaches d = −25 halfway through the period, at t = 4.4. She also crosses the vertical equilibrium line, where d = 0, halfway through each swing, at t = 2.2 and t = 6.6.
Use this information to graph a curve representing Rebecca’s ongoing motion swinging back and forth on her trapeze.
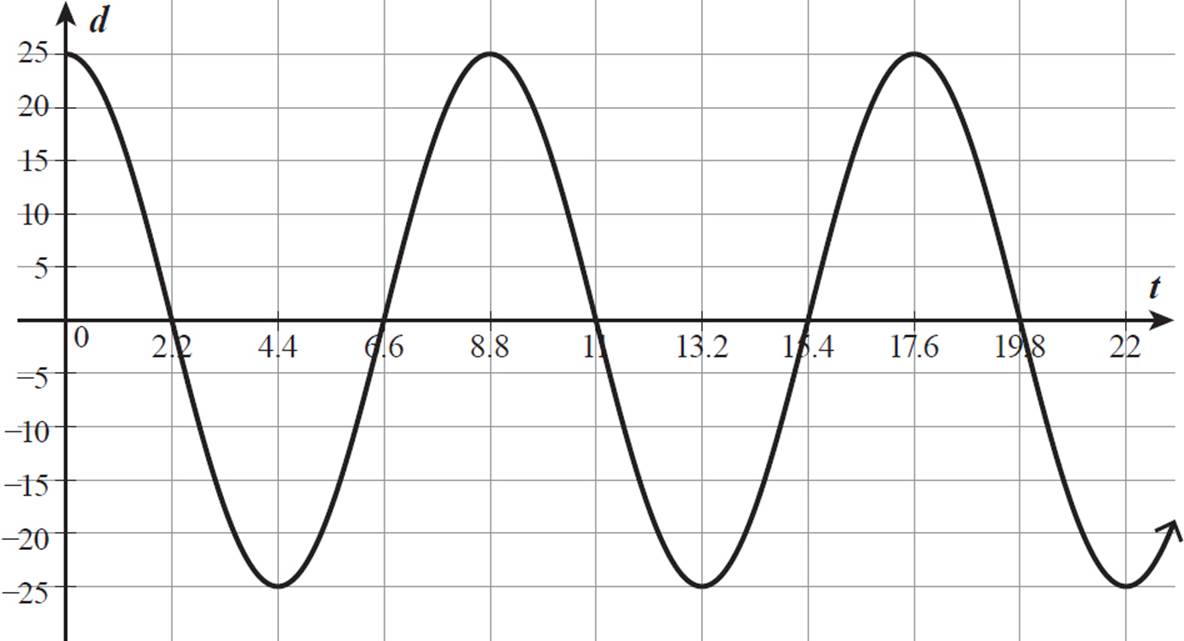
This function starts at its maximum when t = 0, so let’s use a cosine function to describe the graph. This is a cosine function with a midline of 0, an amplitude of 25, and a period of 8.8. The frequency is different from that of a standard cosine function, which has a period of 2π radians. Remember, the period of a cosine function y = a cos b(x − c) + d is 2π/b, so we can set this equal to 8.8 to solve for b.
8.8 = 2π/b
|
8.8b = 2π |
Multiply both sides by b. |
|
b = 2π/8.8 |
Divide both sides by 8.8. |
|
b = 20π/88 |
Multiply both sides by 10 to have a whole number in the denominator. |
|
b = 5π/22 |
Divide the numerator and denominator by 4 to simplify the fraction. |
So, the equation that represents Rebecca’s displacement, in feet, from the equilibrium position, as a function of time, in seconds, is d = 25 cos 5π/22 t.
It is not necessary to
convert the fraction
to be a ratio of whole
numbers, but it
makes the equation
cleaner and easier
to work with.
It takes Rebecca 4.4 seconds to reach the opposite extreme of her swing after leaving the platform. She will return to that position again after a full cycle, 8.8 seconds later, which is a total of 13.2 seconds after leaving the platform (at t = 13.2). And, she will again return to that position another 8.8 seconds later, at t = 22.0.
We could also use
function d = 25 sin
5π/22 (t + 2.2), a sine
function of the same
amplitude, midline,
and period but shifted
2.2 units to the left.
The musical introduction is only 20 seconds long, so she can’t take 22 seconds to get there. In other words, she doesn’t have enough time for 2![]() cycles of swinging back and forth. She can either swing a 1/2 cycle (going directly from the platform across to the opposite extreme) or 1
cycles of swinging back and forth. She can either swing a 1/2 cycle (going directly from the platform across to the opposite extreme) or 1![]() cycles (going across, coming back, and going across again). She wants to swing for as much of the musical introduction as possible, so she should swing 1
cycles (going across, coming back, and going across again). She wants to swing for as much of the musical introduction as possible, so she should swing 1![]() cycles, which takes a total of 13.2 seconds. To arrive there right at the end of the 20-second musical introduction, she must wait for (20 − 13.2) seconds, or 6.8 seconds, after the music begins before starting to swing.
cycles, which takes a total of 13.2 seconds. To arrive there right at the end of the 20-second musical introduction, she must wait for (20 − 13.2) seconds, or 6.8 seconds, after the music begins before starting to swing.
You can also find this
information in the
graph. The points
at which the graph
reaches its minimum,
where d = −25, are
when t = 4.4,
t = 13.2, and t = 22.0.
DRILL
CHAPTER 4 PRACTICE QUESTIONS
Click here to download a PDF of Chapter 4 Practice Questions.
Directions: Complete the following open-ended problems as specified by each question stem. For extra practice after answering each question, try using an alternative method to solve the problem or check your work.
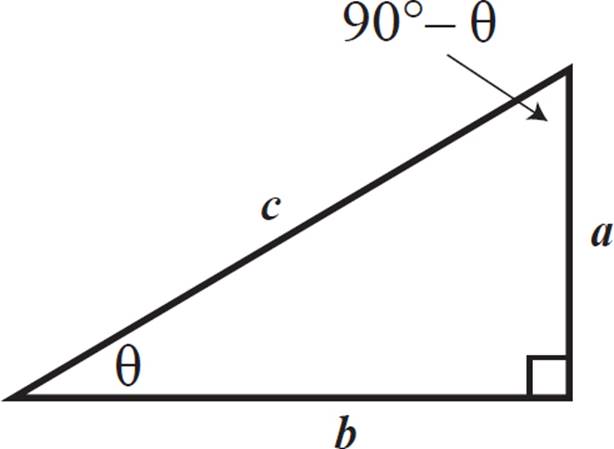
1. Using the triangle diagram below, prove that tan(90 − θ) = 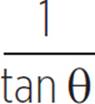 , where θ is the indicated angle measure, in degrees.
, where θ is the indicated angle measure, in degrees.
2. Given csc θ = −4/3 and 3π/2 < θ < 2π, determine the values of the other five trigonometric functions for angle θ. Rationalize the denominators, if needed.
3. The central angle for the subtended arc of the circle x2 + y2 = 144 is 225°. Find the following:
(a) The sine and cosine of the angle
(b) The length of the arc, in radians
4. For each of the following, sketch the graph of the function. Use appropriate scales for axes:
(a) y = 2 sin (x − ![]() )
)
(b) y = 4 − tan ![]()
(c) y = −2 cos (3x + π)
5. Prove each of the following identities, then demonstrate that the identity holds true for the triangle shown below.
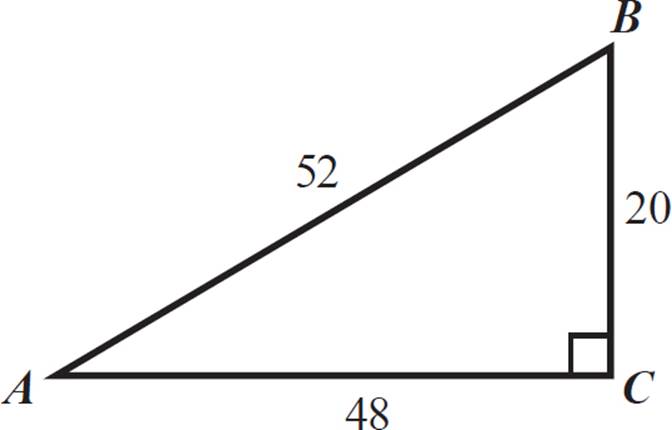
(a) sin θ × sec θ = tan θ
(b) 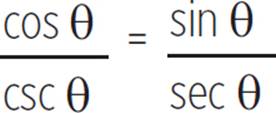
(c) 1 + cot2θ = csc2θ
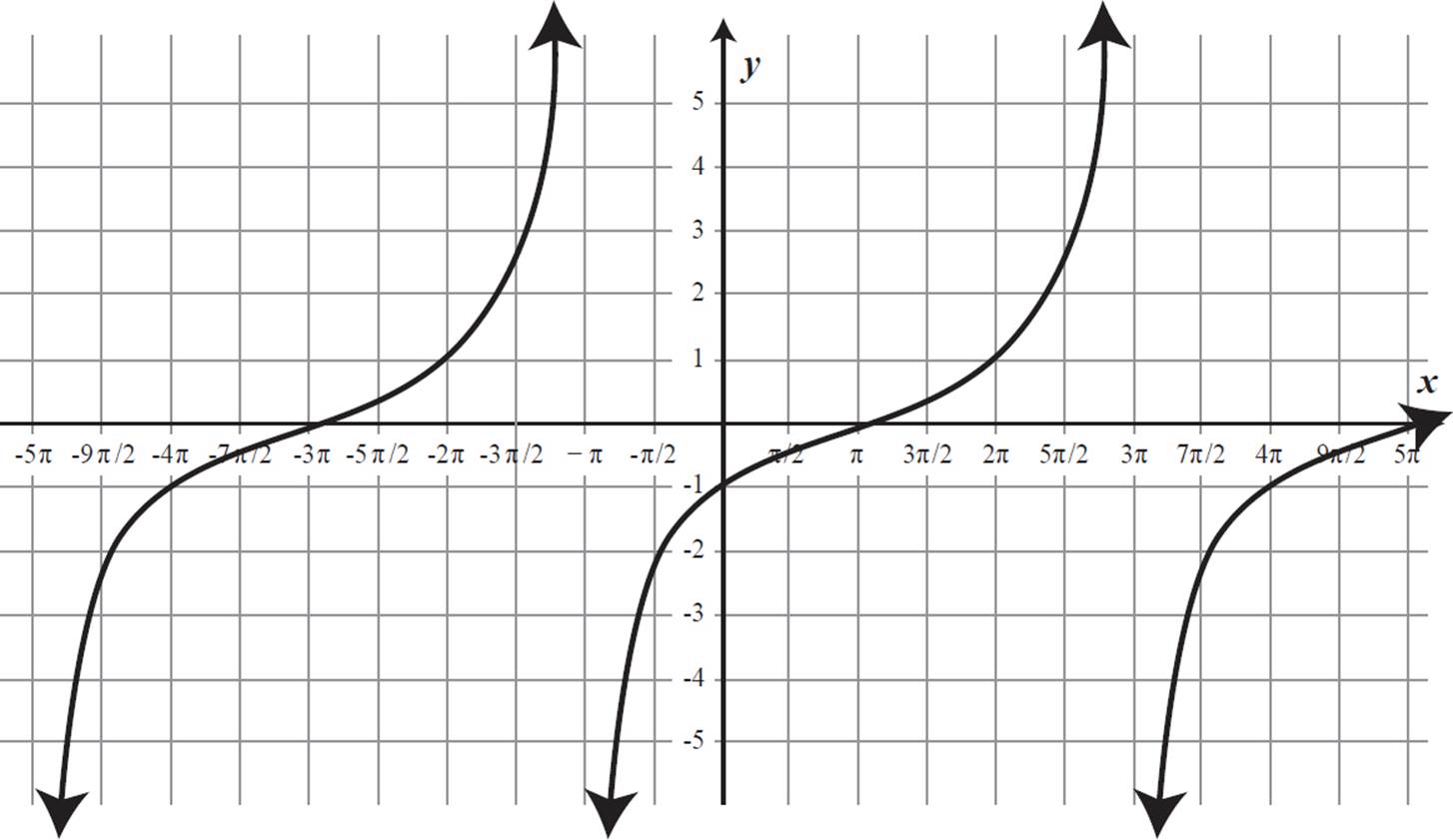
6. Write an equation that describes the trigonometric function graphed below.
7. Shane plays a note of A on his French horn. The sound wave he creates has a frequency of 440 hertz (cycles per second) and an amplitude of 0.5. Assuming a midline of the x-axis, what equation describes the sound wave Shane created?
8. Amy runs around a circular track near a three-story building. The closest Amy comes to the building while running is 6 meters, and this is her starting point. She runs at a steady pace, completing one lap, which is 402 meters long, every 80 seconds, for a total of 5 laps.
(a) Write and graph a trigonometric function that represents Amy’s direct distance from the building as a function of time, in seconds.
(b) The building’s shadow extends 90 meters from the base of the building, shading all of the track that is within this distance of the building. The remainder of the track is in direct sunlight. For approximately how many seconds out of each lap is Amy running in direct sunlight?
SOLUTIONS TO CHAPTER 4 PRACTICE QUESTIONS
1. See proof below.
If you need to remind yourself of the relationship of each side of the triangle to a given angle, you can sketch and label two triangles, as shown. Pay attention to the labeling of the different angles in question. The triangles are identical, but the angle position changes the relation of the sides when producing the trigonometric ratios.
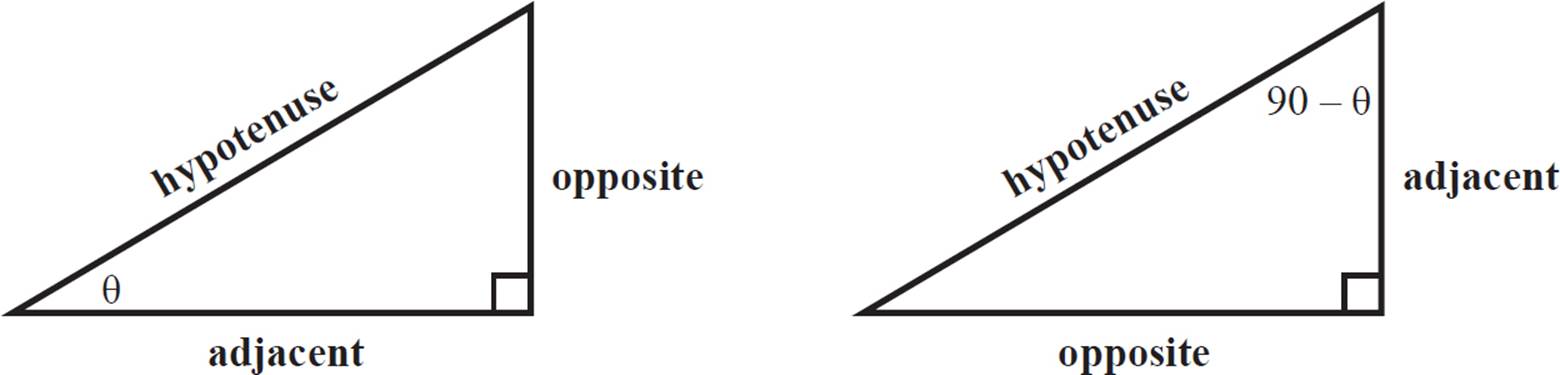
Using the given side lengths a, b, and c, evaluate the required trig functions. You are trying to show that tan (90° − θ) is equal to 1/tan θ, so if you substitute side measures in for each, you’ll get 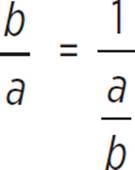 . Multiply by the reciprocal on the right side and there’s your identity.
. Multiply by the reciprocal on the right side and there’s your identity.
2. sin θ = −3/4, csc θ = −4/3, cos θ = 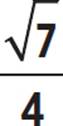 , sec θ =
, sec θ = 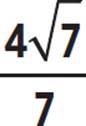 , tan θ =
, tan θ = 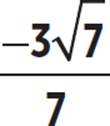 , cot θ = −
, cot θ = −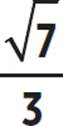
Recall that cosecant is the reciprocal of the sine function, so sin θ = −3/4. One down, four more to go. Sketch a right triangle in the coordinate plane. The measure of θ is between 3π/2 and 2π, so the terminal side is in Quadrant IV. The side opposite θ is 3 units long (with a negative value, because it is below the x-axis), and the hypotenuse (the terminal side) is 4 units long. Using the Pythagorean theorem (a2 + b2 = c2), you can find the length of the third side, which lies on the x-axis.
|
(3)2 + b2 = (4)2 |
Substitute given values. |
|
9 + b2 = 16 |
Evaluate expression. |
|
b2 = 7 |
Subtract 9 from both sides. |
|
b = |
Take the square root of both sides. |
The leg adjacent to the enclosed angle lies along the x-axis to the right of the origin, so it has a positive measure. Now we can sketch the right triangle.
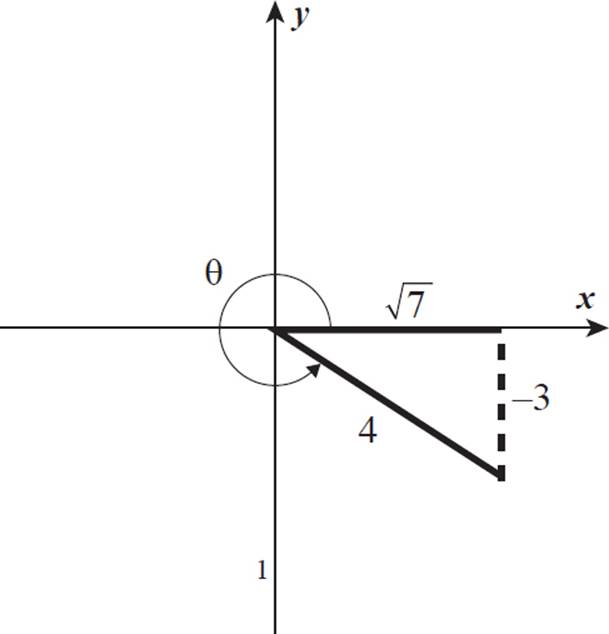
Evaluate the other four functions given these values.
|
Known: |
sin θ = − |
csc θ = − |
|
Remaining: |
cos θ = |
sec θ = |
|
tan θ = |
cot θ = − |
3. (a) (−![]() )/2; (b) 15π
)/2; (b) 15π
(a) Draw an image to get an idea of what is going on and create a right triangle with the x-axis:
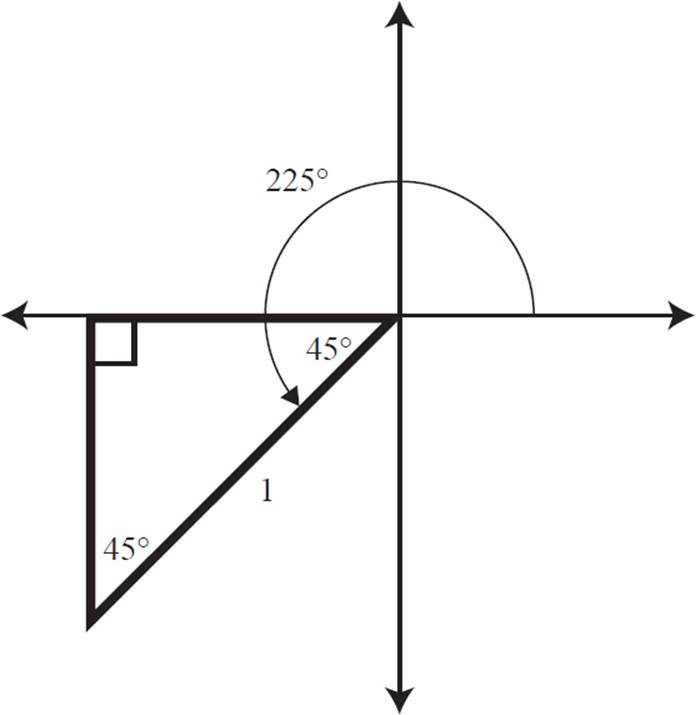
225° opens up to Quadrant III, and when the triangle is created with the x-axis, a 45° angle is created. This makes it an isosceles right triangle, or 45-45-90 special right triangle, with a hypotenuse of 1 in the unit circle. The side lengths of the triangle can be determined using the ratio of s: s: s ![]() . This ratio produces the lengths of the base and height of 1/
. This ratio produces the lengths of the base and height of 1/![]() . Rationalize the denominator by multiplying both numerator and denominator by
. Rationalize the denominator by multiplying both numerator and denominator by ![]() .
.
Note the location of where the triangle is drawn, Quadrant III. In Quadrant III, both the x- and y-coordinates are negative. Label the figure:
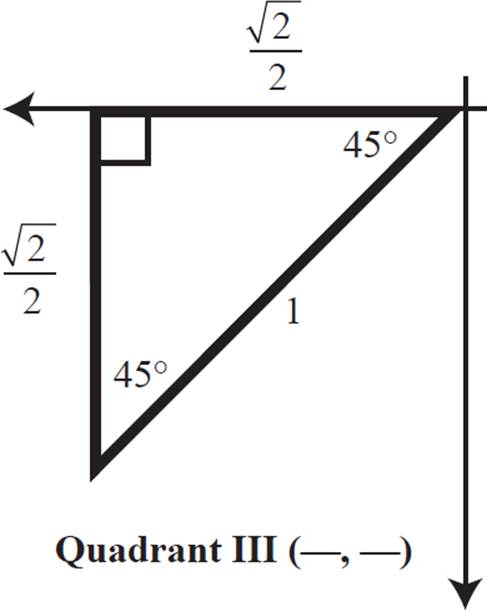
Now, determine the sine and cosine using SOHCAHTOA.

(b) Now, convert to radians by multiplying the given angle (225°) by the conversion proportion of π radians/180°. This yields 5/4 π radians.
A circle described by the equation x2 + y2 = 144, or x2 + y2 = 122, has a radius of 12. The radian measure of a central angle is equal to s/r, where s is the arc length of the subtended arc and r is the radius. Set up an equation using the radius and the radian measure we found.
|
5/4 π = s/12 |
Multiply both sides by 12. |
A 5/4 π central angle subtends an arc of length 15π in the circle x2 + y2 = 144.
4. See the following graphs.
(a) Determine amplitude, period, and any necessary shifts:
Amplitude = |a| = |2| = 2
Period = 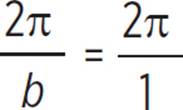 = 2π
= 2π
Shift: Shifted to the right ![]() units
units
(b) Determine amplitude, period, and any necessary shifts:
Amplitude = |a| = |−1| = 1
The negative a value means that the graph is reflected across its midline.
Remember, the parent tangent function has a period of π, not 2π.
Period = 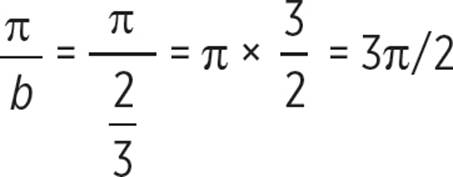 = 3π/2
= 3π/2
Shift: Shifted up 4 units
Remember to reflect the tangent function across the midline, y = 4.
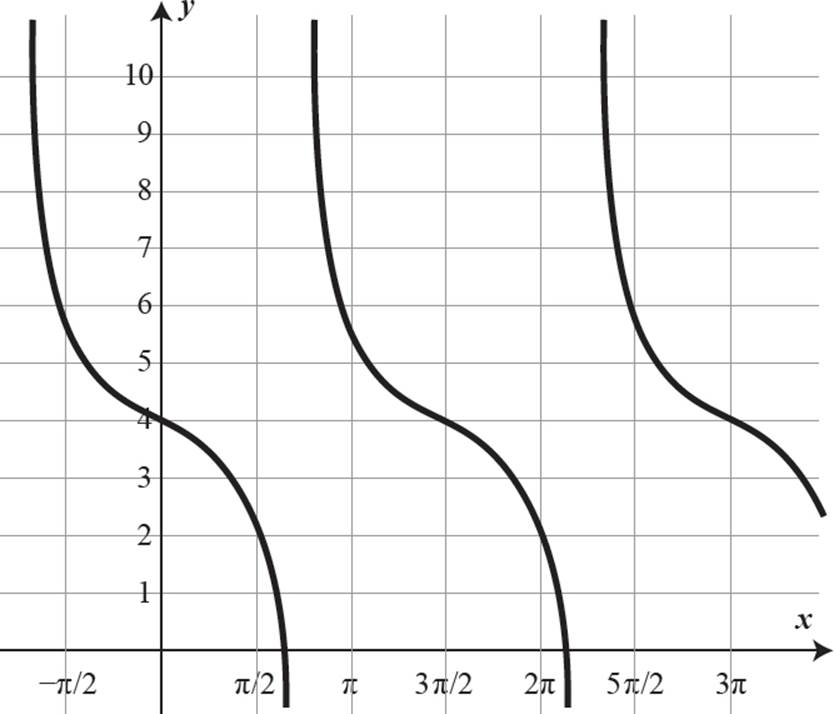
(c) Determine amplitude, period, and any necessary shifts:
Amplitude = |a| = |−2| = 2
The negative a value means that the graph is reflected across its midline, which in this case is the x-axis.
Period = 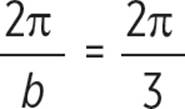
Shift: Shifted to the left π units
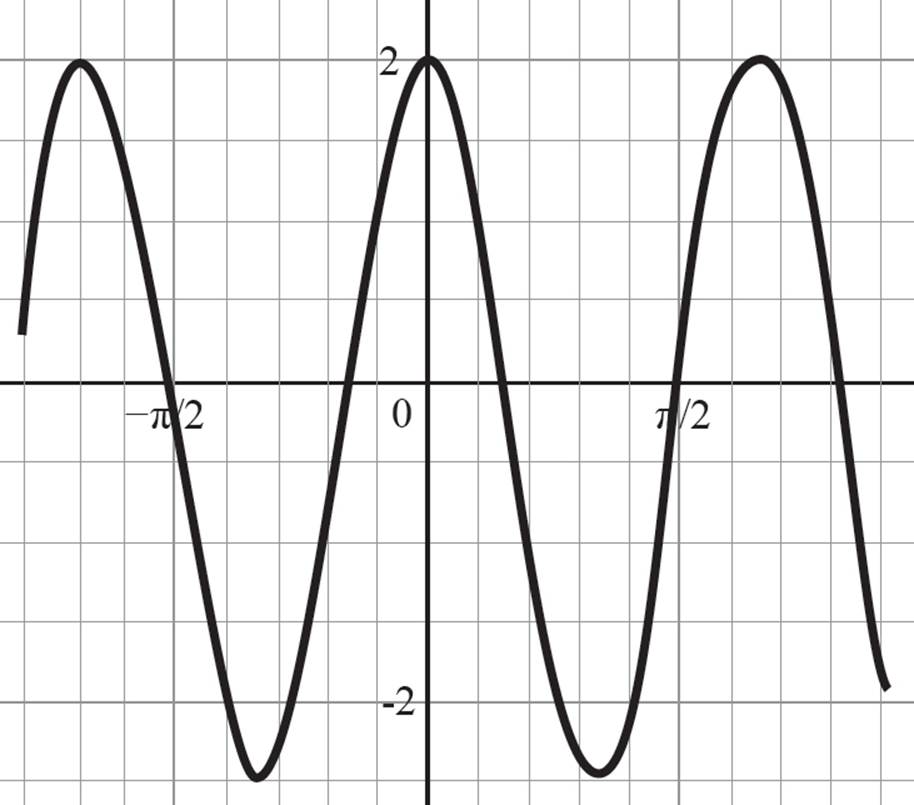
5. See the following proofs.
|
(a) sin θ × sec θ = tan θ |
Given. |
|
sin θ × |
Identity sec θ = |
|
|
Multiply terms on left side of equation. |
|
tan θ = tan θ |
Identity tan θ = |
Now, substitute appropriate side lengths from the given triangle to demonstrate the identity.
|
sin θ × sec θ = tan θ |
Given. |
|
|
SOHCAHTOA and reciprocal identities. |
|
|
Simplification. |
|
(b) = |
Given. |
|
cos θ ÷ csc θ = sin θ ÷ sec θ |
Write fractions as divisions. |
|
cos θ ÷ |
Identities csc θ = |
|
cos θ × sin θ = sin θ × cos θ |
Division is equal to multiplication by reciprocal. |
|
cos θ × sin θ = cos θ × sin θ |
Commutative property of multiplication. |
Now, substitute appropriate side lengths from the given triangle to demonstrate the identity.
|
|
Given. |
|
|
SOHCAHTOA and reciprocal identities. |
|
|
Rewrite division as multiplication by reciprocal. |
|
(c) 1 + cot2 θ = csc2 θ |
Given. |
|
1 + |
Identities cot θ = |
|
1 + |
Square terms. |
|
sin2 θ + cos2 θ = 1 |
Multiply both sides of equation by sin2 θ. |
|
1 = 1 |
Identity sin2 θ + cos2 θ = 1. |
Now, substitute appropriate side lengths from the given triangle to demonstrate the identity.
|
1 + cot2θ = csc2θ |
Given. |
|
1 + |
Reciprocal identities. |
|
1 + |
Perform arithmetic. |
|
|
Put first fraction in common denominator form. |
|
|
Add numerators to produce identity statement. |
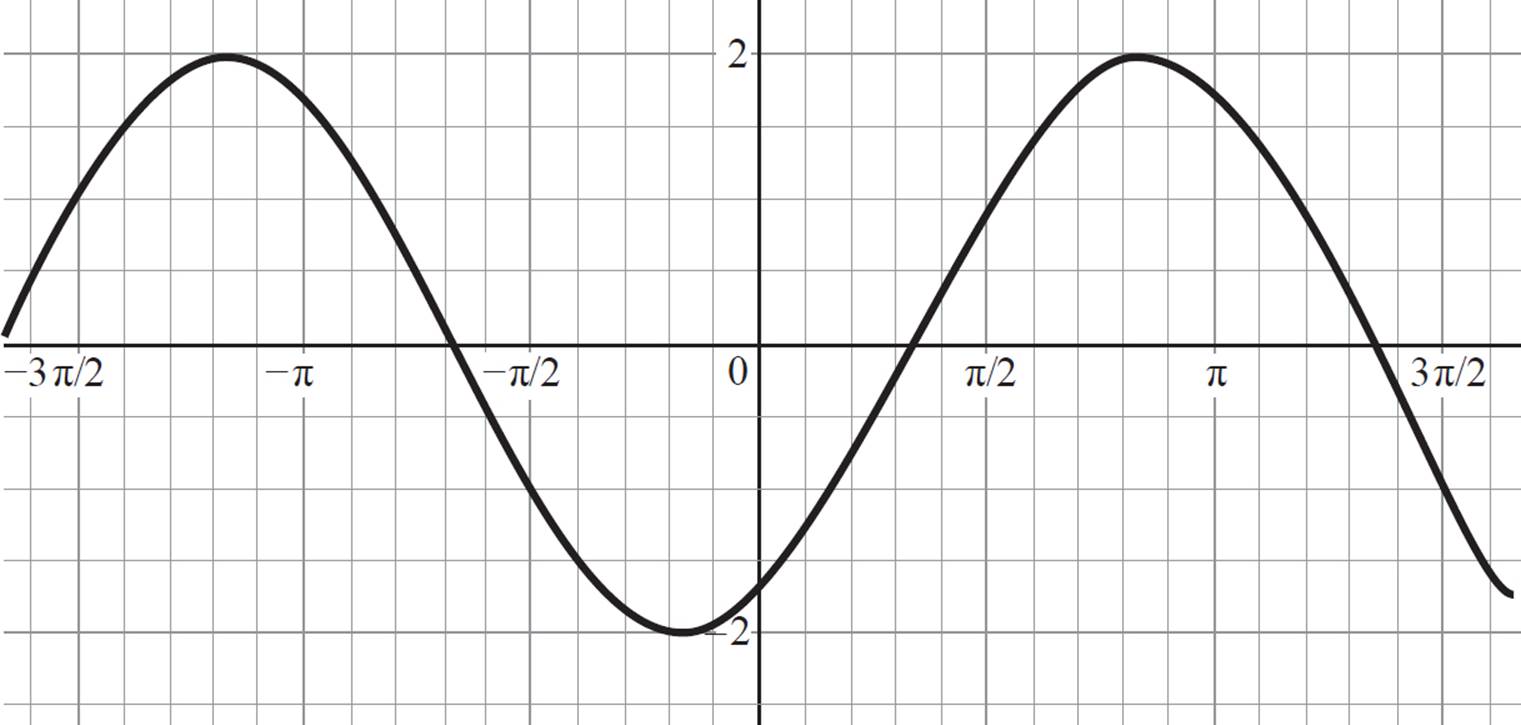
6. y = tan 1/4 (x − π)
This function has asymptotes and is not a continuous wave, so it is a tangent function. The parent tangent function has a period of π, but this function has a much longer period. It has x-intercepts of −3π, π, and 5π, which are each 4π units apart. It completes a full cycle in 4π units, so it has a period of 4π. Find the value of b in y = a tan b(x − c) + d using the fact that the period of a tangent function equals π/b.
|
4π = π/b |
|
|
4πb = π |
Multiply both sides by b. |
|
b = 1/4 |
Divide both sides by 4π and cancel the common factor of π. |
The points of inflection lie on the x-axis, so there is no vertical shift, and d = 0 in y = a tan b(x − c) + d. There is, however, a horizontal shift. The function y = tan x passes through the origin, but the function shown in this graph crosses at x = π instead. It is shifted π units to the right, so c = π. So far, we can write the equation as y = a tan 1/4 (x − π). To find the value of a, use the coordinates of a point on the graph in this equation. Let’s use the point (2π, 1).
|
1 = a tan 1/4 (2π − π) |
Substitute 2π for x and 1 for y. |
|
1 = a tan π/4 |
Simplify 1/4 (2π − π). |
|
1 = a · 1 |
Evaluate tan π/4. |
|
1 = a |
Multiply. |
The value of a is 1, so an equation that describes the graphed function is y = tan 1/4 (x − π).
7. y = 0.5 sin 880πx
A sound wave could be described by a sine or a cosine function, but sine is more commonly used. The frequency of this sound wave is 440 cycles per second, so a single wave is completed in 1/440 second. The period of the sine wave is 1/440 second. The period of a sine function of the form y = a sin b(x − c) + d is equal to 2π/b. Set 2π/b equal to 1/440 to solve for b.
|
2π/b = 1/440 |
|
|
b = 880π |
Cross-multiply. |
With a midline of the x-axis, there is no vertical shift. Where we begin the sine curve on the x-axis does not matter in this situation, so we can begin at the origin, with no horizontal shift of the sine curve. Without any shifts, the function is of the form y = a sin bx. The amplitude is equal to a, so a = 0.5. Substitute this and the value we found for b. Shane’s note of A produced a sound wave described by y = 0.5 sin 880πx.
8. (a) f(x) = −64 cos π/40 x + 70, (b) 32 seconds
(a) It may help to draw a sketch to represent the situation. This is only a rough sketch, because we do not know how much of the track the shadow covers, and nothing is to scale.
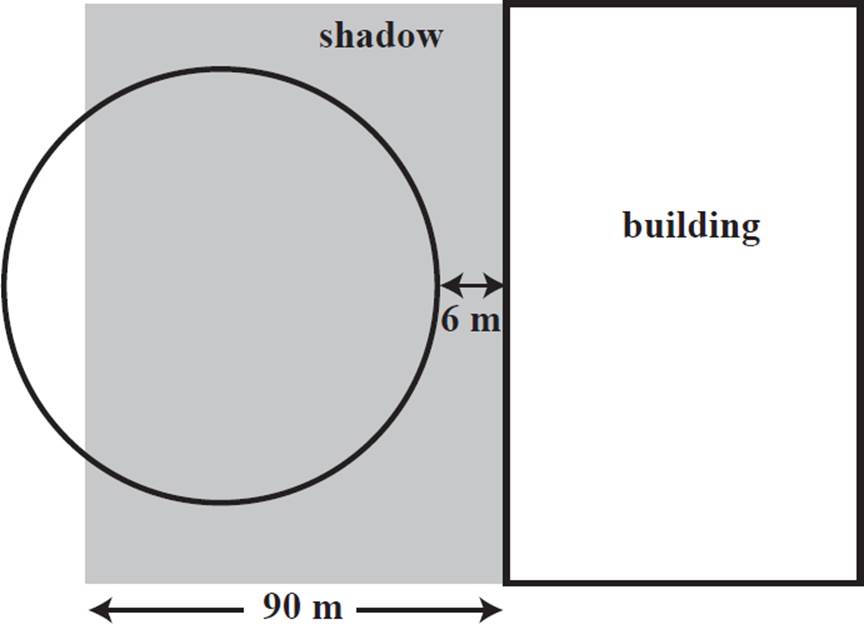
Because Amy is traveling along a circle, her direct distance to the side of the building (a straight line) can be described by a sine or cosine function in terms of the central angle associated with his position. Because she is moving at a steady pace, the central angle varies directly with time in seconds. So, we can write a function for f(x), her direct distance, in meters, from the building, where x is time, in seconds.
At x = 0, when Amy starts her run, she is 6 meters from the building, so f(0) = 6. This is her minimum distance from the building during her laps, so we’ll use a cosine curve reflected across its midline.
Amy completes one lap of the track in 80 seconds, so the cosine curve has a period of 80 seconds. The period of a cosine function is 2π/b, where b is the coefficient of x in the function, so 2π/b = 80. Multiplying both sides by b gives us 80b = 2π, so b = π/40.
The circumference of Amy’s circular path on the track is 402 meters, and the circumference of a circle is 2πr, so 2πr = 402, and r = 201/π, which is approximately equal to 64. The radius of the circular track is 64 meters. So, the diameter of the track is 128 meters. Amy’s furthest point from the building is a distance of the diameter plus 6 meters: 128 + 6 = 134. The cosine curve will have a minimum f(x)-value of 6 and a maximum f(x)-value of 134, so its midline will be at their average: (6 + 134) ¸ 2 = 70. Its amplitude is the difference between the midline and each extreme (134 − 70 or 70 − 6), 64.
We’ll write the function in the form f(x) = a cos b(x − c) + d. The amplitude, |a|, is 64, but to reflect the cosine curve across the midline, a must be negative: −64. The b-value is π/40. There is no horizontal shift, so c = 0. The midline is 70, so the vertical shift, or d, is 70. The function that describes Amy’s direct distance, in meters, from the building as a function of time, in seconds, is f(x) = −64 cos π/40 x + 70. Its graph is below, showing 5 full cycles for Amy’s 5 laps around the track.
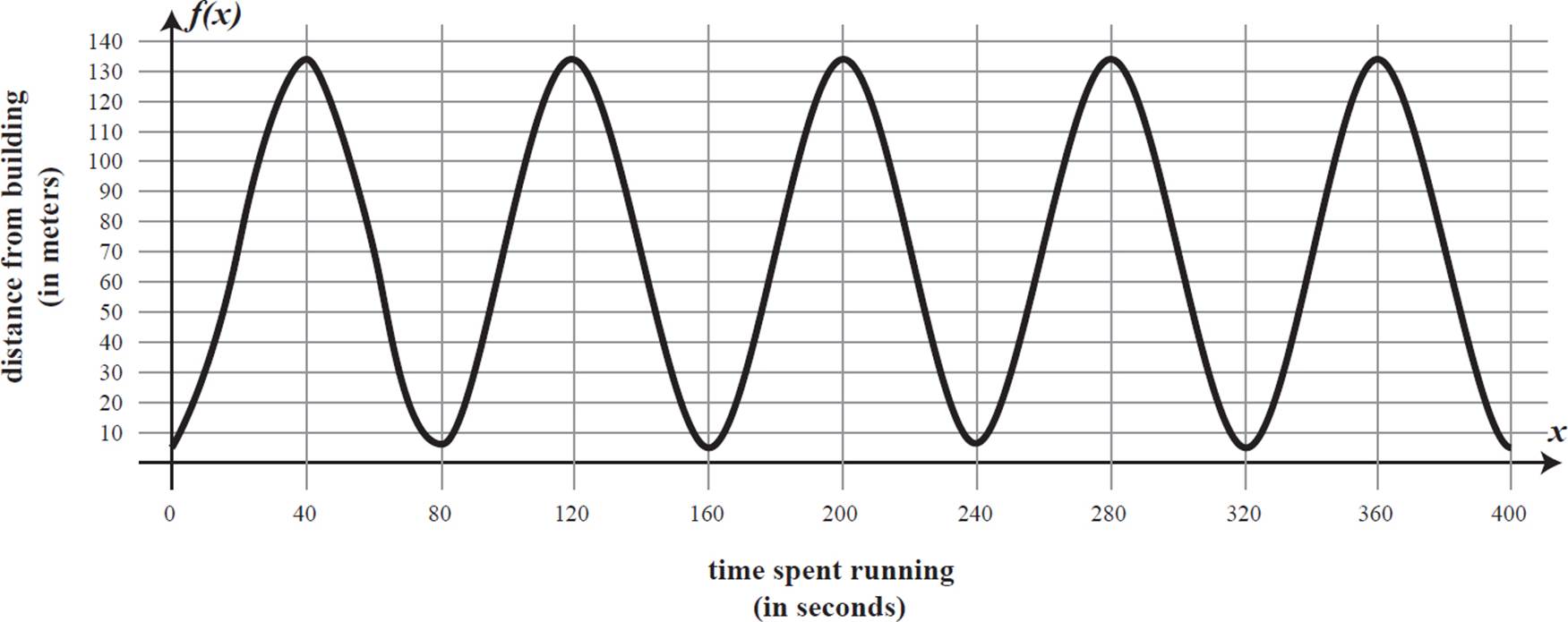
(b) The shadow extends 90 meters from the base of the building, or to f(x) = 90. The portions of the cosine curve where f(x) > 90 correspond to when Amy is in direct sunlight. We can find the x-values in the first cycle (between 0 and 80) where f(x) = 90, then subtract to find the time difference.
|
−64 cos π/40 x + 70 = 90 |
Set cosine function equal to 90. |
|
−64 cos π/40 x = 20 |
Subtract 70 from both sides. |
|
cos π/40 x = −0.3125 |
Divide both sides by −64. |
|
π/40 x ≈ 1.89 |
Use your calculator to find cos−1 in radians. |
|
x ≈ 24 |
Multiply both sides by 40/π. |
We know the cosine curve is symmetrical with respect to any vertical line through a maximum or minimum, so it is symmetrical with respect to x = 40. The point where the curve first reaches 90 is when x = 24, which is 16 units to the left of 40, so it will come back down to 90 the same distance to the right of 40: 40 + 16 = 56. Amy will be in direct sunlight from x = 24 to x = 56, which is a time period of 56 − 24 = 32. Amy runs in direct sunlight for 32 seconds out of each lap.
REFLECT
Congratulations on completing Chapter 4!
Here’s what we just covered.
Rate your confidence in your ability to
• Use the relationship between radius, radian measure, and arc length to solve for any one of these values for a given circle and central angle
1 2 3 4 5
• Convert between degrees and radians for any angle measure
1 2 3 4 5
• Find the value of the sine, cosine, tangent, cosecant, secant, or cotangent, where it exists, for any real number
1 2 3 4 5
• Graph sine, cosine, and tangent functions using information about the period, midline, amplitude, horizontal shift, and any reflection, and write an equation to describe a given sine, cosine, or tangent function
1 2 3 4 5
• Prove and apply trigonometric function identities
1 2 3 4 5
• Write and use sine and cosine functions to represent real-life situations and solve problems
1 2 3 4 5
If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.
 Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.
Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.
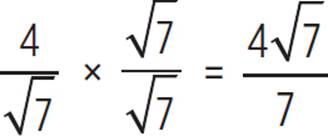
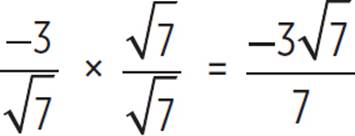
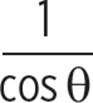 = tan θ
= tan θ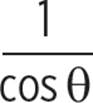 .
.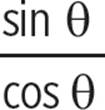 = tan θ
= tan θ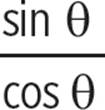 .
.
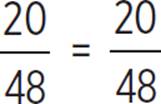
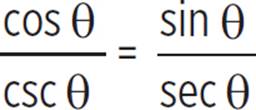
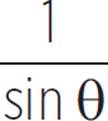 = sin θ ÷
= sin θ ÷ 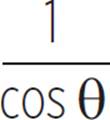
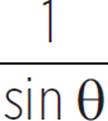 and sec θ =
and sec θ = 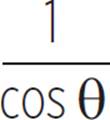 .
.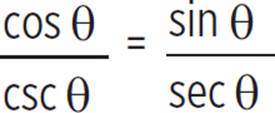
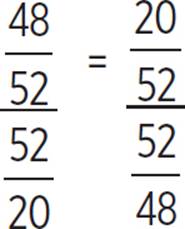
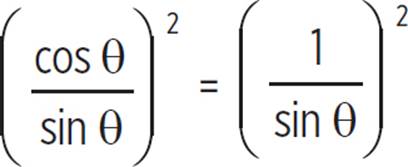
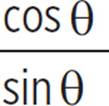 and csc θ =
and csc θ =