High School Algebra II Unlocked (2016)
Chapter 6. More Functions
Lesson 6.3. Exponential Functions
REVIEW
Rules of exponents, for real number b, b > 0, and rational numbers m and n:
b1 = b
b0 = 1
b−n = 1/bn
bm ⋅ bn = bm + n
(bm)n = bmn
COMMUTATIVE PROPERTY OF MULTIPLICATION:
a ⋅ b = b ⋅ a
“Percent” means “out of 100,” so to convert a given percent to a decimal, divide by 100, or move the decimal point two places to the left.
An exponential function is a function in which the independent variable (x) is in the exponent of a constant base that is greater than 0 and not equal to 1. The most basic form of an exponential function is f(x) = bx (with b > 0 and b ≠ 1).
The base must be positive, because a negative base would alternately produce positive and negative function values respectively for even and odd values of x. The base cannot equal 0, because the expression 0x is equal to 0, regardless of the value of x, creating a constant function instead of an exponential function. Likewise, a base of 1 in f(x) = bx creates the constant function f(x) = 1, because 1 raised to any power is just 1.

Exponential functions
were briefly introduced
in Lesson 5.4, as the
inverse of logarithmic
functions. Here
we will explore
exponential functions
in greater detail.

Graph the exponential functions g(x) = 3x and h(x) = (1/3)x. What is the relationship between the two graphs?
First, create a table of values for each function. Use x-values that provide easy function calculations.
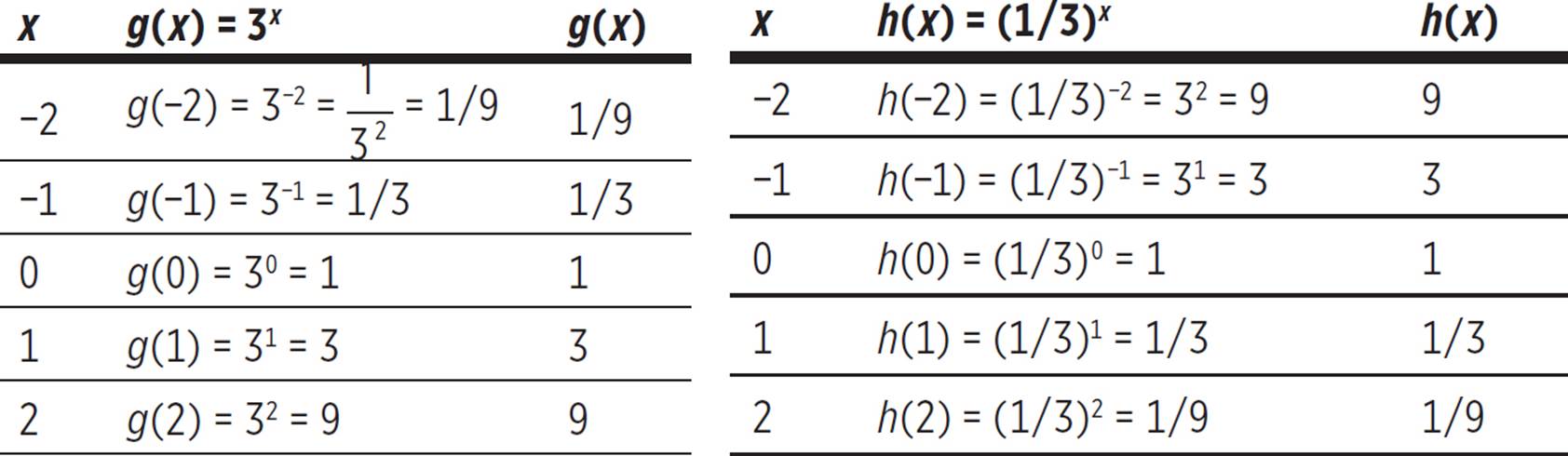
The graphs of g(x) = 3x (passing through (−2, 1/9), (−1, 1/3), (0, 1), (1, 3), and (2, 9)) and h(x) = (1/3)x (passing through (−2, 9), (−1, 3), (0, 1), (1, 1/3), and (2, 1/9)) are shown on the coordinate grid below.
Remember that any
value b raised to
the power of −1 is
1/b. So, 3−2, which
is the same as (32)−1,
is equal to ![]() .
.
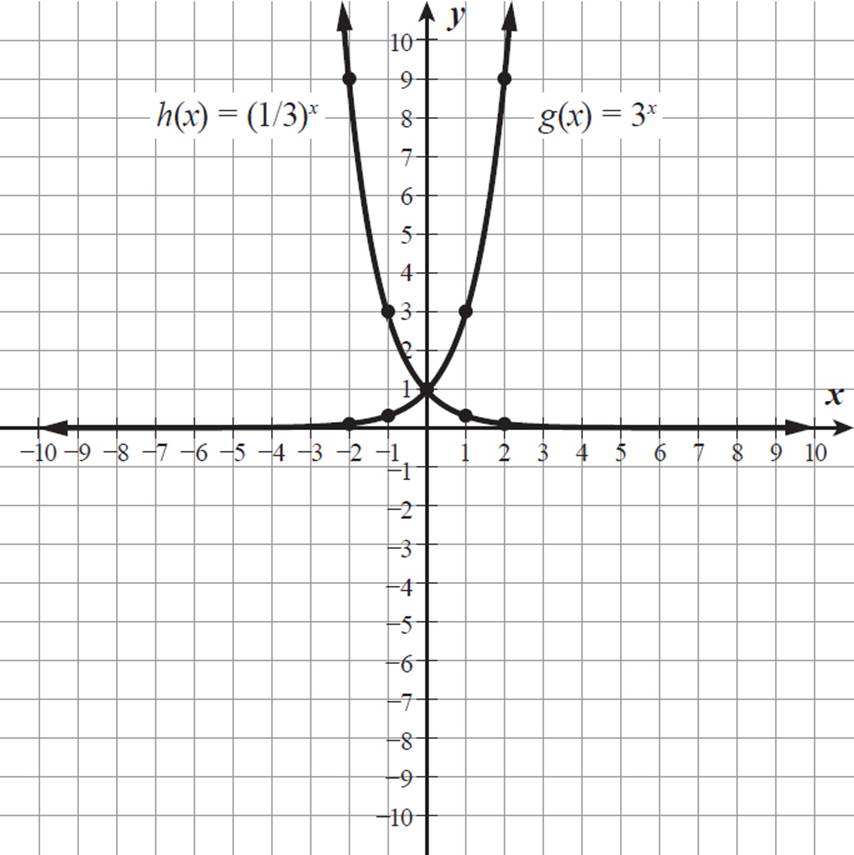
The graphs are reflections of one another across the y-axis.
Because 1/3 = 3−1, the
function h(x) = (1/3)x
can be rewritten as
h(x) = 3−x. This is the
function g(x) = 3x
with x replaced by −x,
or g(−x). The graph
of g(−x) = 3−x (also
known as h(x)) is the
reflection of
g(x) = 3x across
the y-axis.

The function g(x) = 3x is always increasing, and the function h(x) = (1/3)x is always decreasing.
An exponential function is either always increasing or always decreasing. A function of the form f(x) = bx is always increasing if b > 1 and always decreasing if 0 < b < 1.
An exponential function in the form f(x) = bx has a function value of 1 when x = 0. In other words, any function of the form f(x) = bx passes through the point (0, 1).

Using graphing technology, compare the graphs of p(x) = 2x, q(x) = 3 ⋅ 2x, and r(x) = (3 ⋅ 2)x.
The function r(x) = (3 ⋅ 2)x can be rewritten as r(x) = 6x.
The graphs of p(x) = 2x, q(x) = 3 ⋅ 2x, and r(x) = 6x are shown below.
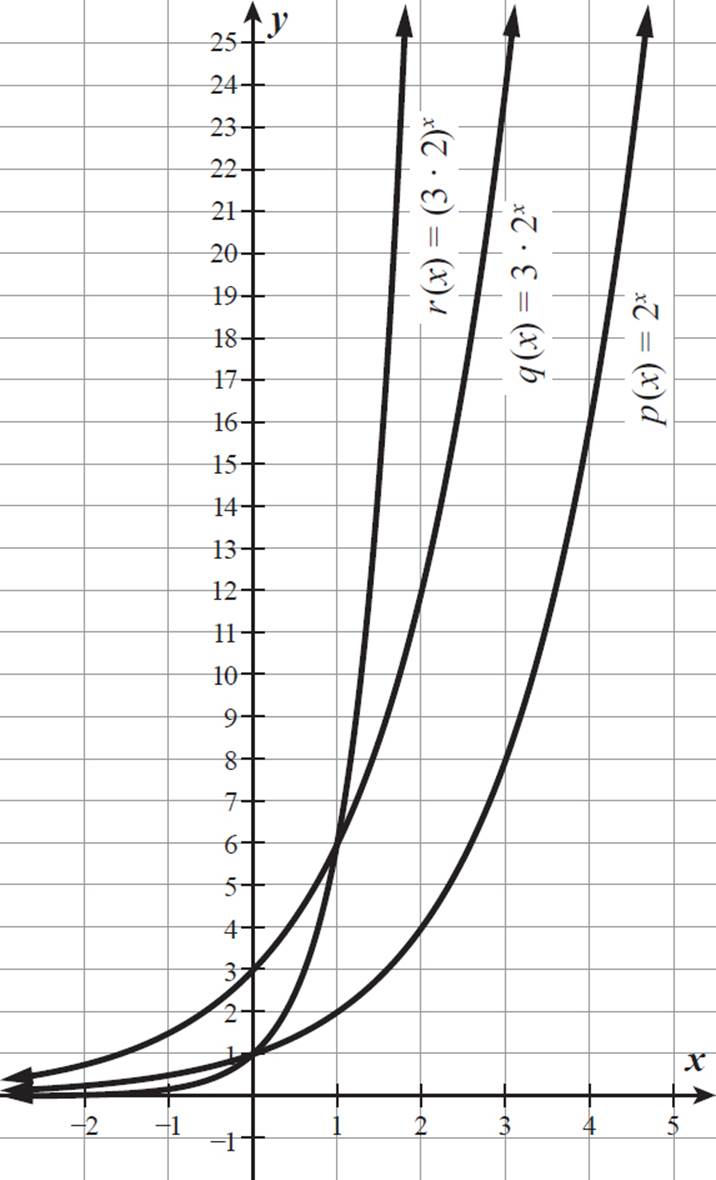
Both q(x) = 3 ⋅ 2x and r(x) = (3 ⋅ 2)x increase in value more quickly than p(x) = 2x, with function graphs that appear more narrow. The function r(x) = (3 ⋅ 2)x increases more quickly than q(x) = 3 ⋅ 2x to the right of x = 1. This makes sense, because (3 ⋅ 2)x is the same as 3x ⋅ 2x. For x-values greater than 1, 3x will be greater than 3, so 3x ⋅ 2x will be greater than 3 ⋅ 2x.
Both p(x) = 2x and r(x) = (3 ⋅ 2)x (or 6x) have a y-intercept of 1, as do all functions of the form f(x) = bx, but q(x) = 3 ⋅ 2x has a y-intercept of 3. Its exponential component, 2x, is equal to 1 when x = 0, but that value gets multiplied by 3 in the function.

An exponential function of the form f(x) = a ⋅ bx has a y-intercept of (0, a). For |a| > 1, it increases (or decreases) more quickly than f(x) = bx, and for 0 < |a| < 1, it increases (or decreases) more slowly. A negative value of a reflects the function across the x-axis.
All of the exponential functions we have looked at so far have had one arm approaching a horizontal asymptote of y = 0, or the x-axis. However, a vertical shift of any of these graphs would result in a different horizontal asymptote.
An exponential
function of the form
y = a ⋅ bx always has a
horizontal asymptote
of the x-axis, because
bx approaches 0 for
one end of the graph
(as x approaches −∞,
if b > 1; and as
x approaches
∞, if b < 1).

Graph the function f(x) = 1/2 ⋅ 2x − 8. What are the domain, range, x-intercept, and y-intercept of this function?
This function should increase at half the level of y = 2x, but also shift vertically downward 8 units. Let’s create a table of values to find points on the graph.
|
x |
f(x) = 1/2 ⋅ 2x − 8 |
f(x) |
|
0 |
f(0) = 1/2 ⋅ 20 − 8 = 1/2 ⋅ 1 − 8 = 1/2 − 8 = −7 1/2 |
−7 1/2 |
|
1 |
f(1) = 1/2 ⋅ 21 − 8 = 1/2 ⋅ 2 − 8 = 1 − 8 = −7 |
−7 |
|
2 |
f(2) = 1/2 ⋅ 22 − 8 = 1/2 ⋅ 4 − 8 = 2 − 8 = −6 |
−6 |
|
3 |
f(3) = 1/2 ⋅ 23 − 8 = 1/2 ⋅ 8 − 8 = 4 − 8 = −4 |
−4 |
|
4 |
f(4) = 1/2 ⋅ 24 − 8 = 1/2 ⋅ 16 − 8 = 8 − 8 = 0 |
0 |
|
5 |
f(5) = 1/2 ⋅ 25 − 8 = 1/2 ⋅ 32 − 8 = 16 − 8 = 8 |
8 |
The horizontal asymptote for y = 1/2 ⋅ 2x would be at y = 0. The graph of f(x) = 1/2 ⋅ 2x − 8 is the graph of y = 1/2 ⋅ 2x shifted 8 units down, so f(x) has a horizontal asymptote of y = −8.
The graph of f(x) = 1/2 ⋅ 2x − 8, with a horizontal asymptote of y = −8 and passing through the points (0, −7 1/2), (1, −7), (2, −6), (3, −4), (4, 0), and (5, 8), is shown below.
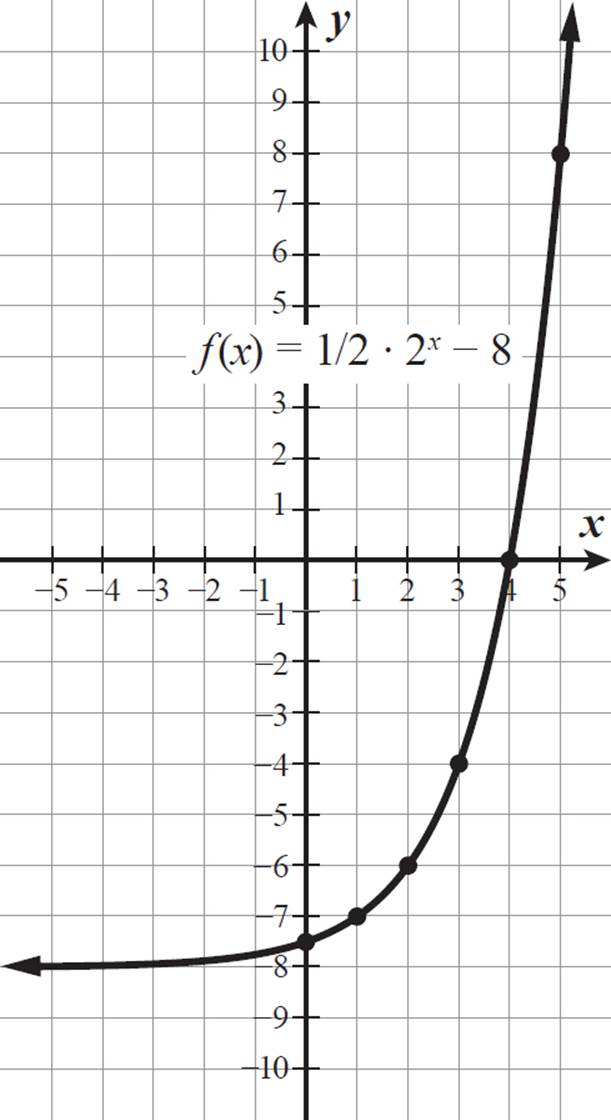
The domain of f(x) = 1/2 ⋅ 2x − 8 is all real numbers, and its range is all real numbers greater than −8.
We found both the y-intercept and the x-intercept when creating our table of values. The point (0, −7 1/2) is the y-intercept of f(x), and the point (4, 0) is the x-intercept.

Any exponential function of the form f(x) = a ⋅ bx + c has a domain of all real numbers and a range of all real numbers greater than c (in the case that a is positive) or all real numbers less than c (in the case that a is negative). One arm extends toward either positive or negative infinity, and the other arm approaches a horizontal asymptote of y = c.
As with other types of functions, f(x + k) represents a horizontal shift of f(x) a total of k units: to the left if k is positive and to the right if k is negative. However, because of the nature of exponential functions, the function equation can be rewritten to eliminate the constant added to x in the exponent, by adjusting the value of a.
The expression
bx + k is equal to
bx ⋅ bk, so if b and k
are both constants,
bk is also a constant
and can be moved
out front as part of
the coefficient of bx.

What equation describes the exponential function, base 3, shown below?
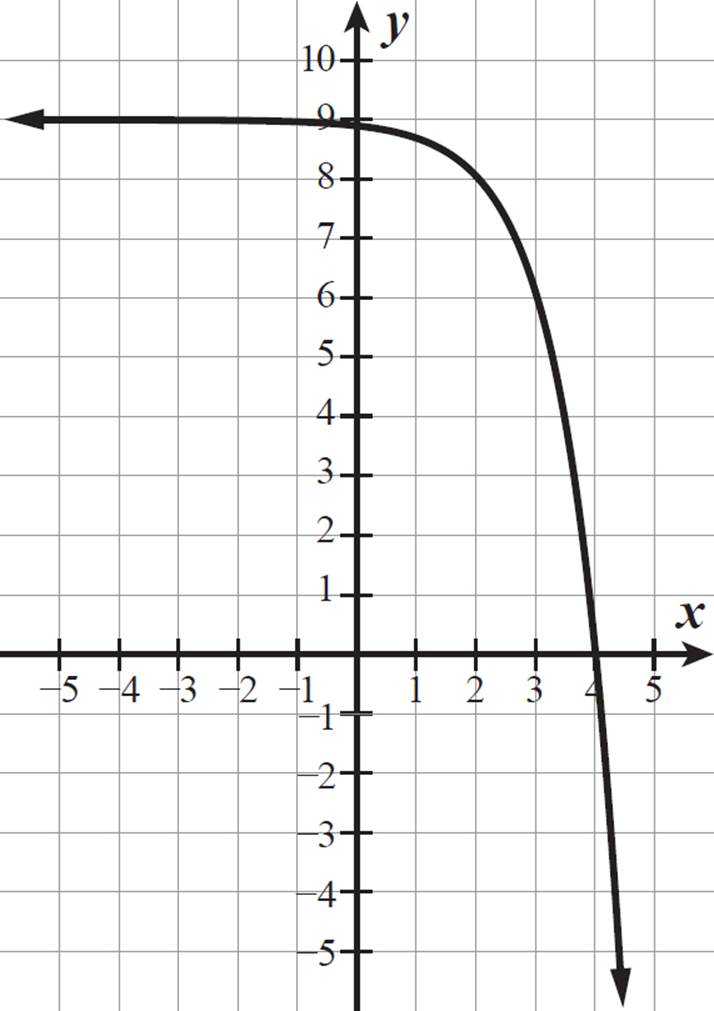
The function has a horizontal asymptote at y = 9, so c in y = a ⋅ bx + c is equal to 9. We were also given that b = 3. So, the equation is in the form y = a ⋅ 3x + 9.
The function is always decreasing, so a is negative.
Let’s use points along the graph to determine the exact value of a. The graph passes through the points (2, 8), (3, 6), and (4, 0), so we can substitute each pair of coordinates into the equation y = a ⋅ 3x + 9.
|
8 = a ⋅ 32 + 9 |
6 = a ⋅ 33 + 9 |
0 = a ⋅ 34 + 9 |
|
8 = 9a + 9 |
6 = 27a + 9 |
0 = 81a + 9 |
|
−1 = 9a |
−3 = 27a |
−9 = 81a |
|
−1/9 = a |
−1/9 = a |
−1/9 = a |
The value of a is −1/9, so the equation of this exponential function is y = −1/9 ⋅ 3x + 9.
We could have used
just one coordinate
pair to solve for a, but
using two or three
helps confirm that we
have solved correctly.

Alternatively, once we determined that the equation is in the form y = a ⋅ 3x + 9 with a < 0, we could compare the given graph to the graph of y = −3x + 9, which is shown below.
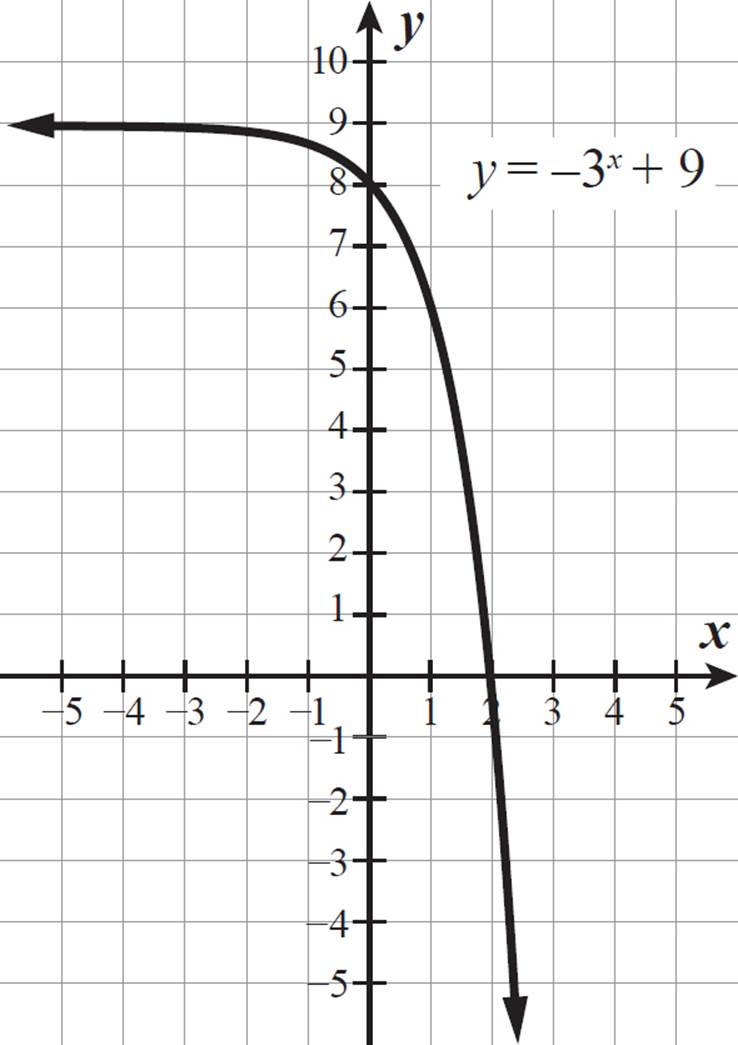
The graph of y = −3x + 9 passes through (0, 8), (1, 6), and (2, 0), and it has a horizontal asymptote of 9. The given graph is therefore the graph of y = −3x + 9 shifted 2 units to the right. So, the equation of the mystery function must be y = −3x − 2 + 9. This equation looks different from what we found before, but they are actually the same equation, as shown below.
|
y = −(3x − 2) + 9 |
Add parentheses to isolate the exponential term. |
|
y = −(3x ⋅ 3−2) + 9 |
Rewrite 3x − 2 using the rule that bx + y = bx ⋅ by. |
|
y = −(3x ⋅ 1/9) + 9 |
Evaluate 3−2. |
|
y = −1/9 ⋅ 3x + 9 |
Use the commutative property of multiplication to switch 3x and 1/9. |
This is the same equation we found above.
EXPONENTIAL FUNCTIONS IN THE REAL WORLD
Exponential functions in the real world are modeling either exponential growth or exponential decay. Most often, an exponential function representing a real-life situation will use time values as the input values (the x-values). The function values typically represent a quantity of some sort (such as mass, population, area, or money), so they are usually positive values, which means that a function of the form f(x) = a ⋅ bx representing the situation has a positive value of a.
In most real-life situations, there is no constant added to a ⋅ bx. Decay functions are heading toward an asymptote of 0. Growth functions are shown in relation to some set initial amount or population, but that is given by the variable a in f(x) = a ⋅ bx. When x = 0, bx = 1, so the function value is equal to a at time = 0.
A function of the form f(x) = a ⋅ bx, with a > 0, represents exponential growth if b > 1 and exponential decay if 0 < b < 1.
Alternatively, exponential decay can be expressed as f(x) = a ⋅ b−x, with a > 0 and b > 1. Remember, b−x = (1/b)x, so if b > 1, both of these expressions represent exponential decay.
Exponential functions representing continuous growth or decay often use e for the base.

In Lesson 5.5, Example
24, we looked at an
example of exponential
decay (of the weight
of iodine-131 in
relation to time),
and the exponential
function representing
that decay had a
base of 1/2 raised
to the power of x.

Here is how you may see exponential functions on the SAT.
The population of a certain songbird in North America is decreasing at a rate of 5% per year. If there are currently 450,000 of these birds in North America, and x represents the number of years, which of the following expressions best represents the trend in the North American population of this songbird?
A) 450,000(0.05)x
B) 450,000(0.05)x
C) 450,000(0.95)x
D) 450,000(0.95)x

Jeremy has $2,000 to invest. He is trying to choose between an account at Savers Bank, which offers 1.5% interest compounded continuously, and Cash Cow Bank, which offers 1.0% interest compounded biannually for balances under $2,500 and 2.0% interest compounded biannually for balances of $2,500 or more. (The interest rate changes automatically when an existing balance reaches $2,500.)
Investing a principal, P, in an account with an interest rate of r (expressed as a decimal) compounded n times per year for t years results in a total balance, A, given by the formula A = P(1 + r/n)nt. If the interest is compounded continuously, the formula is A = Pert.
Write and graph a function representing the balance over the next 50 years in a Savers Bank account if Jeremy were to invest his $2,000 there. Write a piecewise-defined function representing the balance in a Cash Cow Bank account if Jeremy were to invest his $2,000 there. (Assume in both cases that he will make no further deposits or withdrawals.) Graph the piecewise-defined function on the same coordinate grid as the Savers Bank account function. For what period of investment time is the Savers Bank account a better deal for Jeremy? For what period of investment time is the Cash Cow Bank account a better deal? (Answer to the nearest whole year.)

In Lesson 6.2, we
learned about
piecewise-defined
functions. Jeremy’s
account balance in
the Cash Cow Bank
account is an example
of a real-life situation
involving a piecewise-
defined function.
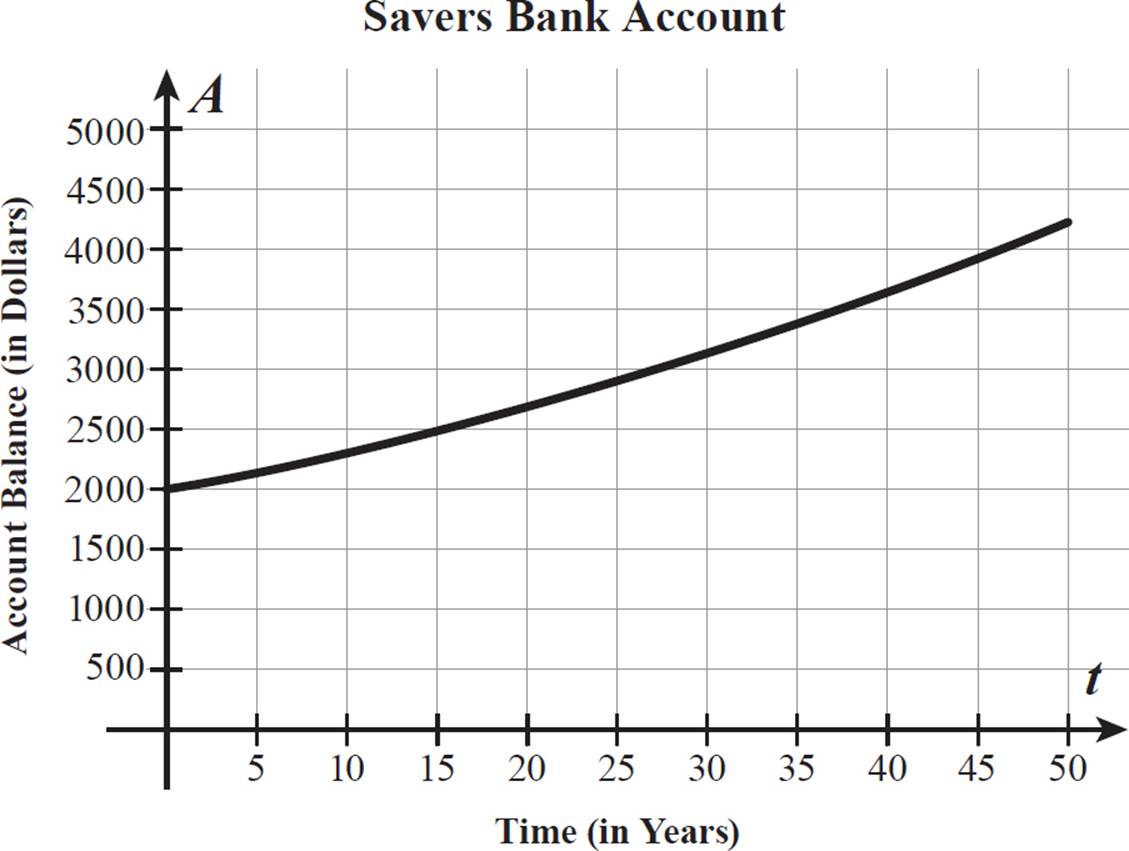
Let’s start by using the continuously compounded interest formula, A = Pert, to write an equation representing Jeremy’s potential investment at Savers Bank. For an investment of $2,000 at an interest rate of 1.5% compounded continuously, P = 2000 and r = 0.015, so the function is A = 2000e0.015t. Using graphing technology, we can graph this exponential function for a period of 50 years, as shown on the coordinate grid below.
Convert 1.5% to a
decimal by dividing
by 100, or moving
the decimal point
two places to the
left: 1.5% = 0.015.
Jeremy’s potential investment in a Cash Cow Bank account is modeled by a piecewise-defined function because the interest rate, and therefore the function equation, changes when the balance reaches $2,500. This is an A-value, so we will need to solve for what the t-value is when A reaches 2500.
First, though, we must write an equation for the account balance when the interest rate is still 1.0% (r = 0.01). Again, the initial investment, P, is equal to 2000. The interest for the Cash Cow Bank account is compounded biannually, which means that it is compounded twice per year, so n = 2. Using the formula A = P(1 + r/n)nt, we get A = 2000(1 + 0.01/2)2t, which simplifies to A = 2000(1.005)2t.
Now we must find the time, t, when the interest rate changes. This happens when the account balance reaches $2,500, so substitute 2500 for A and solve for t.
|
2500 = 2000(1.005)2t |
Substitute 2500 for A in A = 2000(1.005)2t. |
|
1.25 = (1.005)2t |
Divide both sides by 2000. |
|
log1.0051.25 = 2t |
Take the logarithm, base 1.005, of both sides. |
|
|
Use the change of base property to rewrite with common logarithms. |
|
2t ≈ 44.74 |
Use your calculator to evaluate |
|
t ≈ 22.37 |
Divide both sides by 2. |
So, the account balance will reach $2,500 after about 22.37 years, or about 22 years and 4.4 months. However, the interest is only compounded twice per year, and the total number of times it is compounded must be a whole number. In the function A = 2000(1.005)2t, the expression 2t represents the number of times interest is compounded, so 2t must be a whole number. Our solution for 2t above, 44.74, must be rounded up to the next whole number, 45, so our solution becomes t = 22.5. After the compounding that occurs after 22 1/2 years (the 45th compounding), the account balance will be over $2,500.

In Lesson 5.3, we
learned how to use the
logarithmic change of
base property. Here
we make use of it to
perform calculations
related to a real-life
situation involving
interest rates.

To find 5% of the current number of these songbirds, you would multiply 450,000 by 0.05. However, that tells you how many fewer songbirds there will be one year from now. Instead, we want to write an equation that gives the resulting population after x years. If the number decreases by 5% each year, then each year’s population is 95% of the previous year’s population.
For each increase of x by 1 (for each year that passes), the bird population is multiplied by 0.95. (To find 95% of a value, multiply by 0.95.) A repeated multiplication by the same number can be expressed using an exponential term. The number is the base, and the exponent tells you how many times it is used as a factor. So, multiplying the initial songbird population by 0.95 a total of x times is written as 450,000(0.95)x. An exponential function for f(x), the songbird population after x years, is f(x) = 450,000(0.95)x. The correct answer is (D).
For t = 22.5, the equation A = 2000(1.005)2t becomes A = 2000(1.005)45. Use your calculator to compute this amount. The balance, A, in the account at t = 22.5 is $2,503.24, rounded to the nearest cent.
At this point, the account rules change to a 2.0% interest rate compounded biannually. For the new initial balance (for this equation) of $2,503.24, the formula A = P(1 + r/n)nt produces the equation A = 2503.24(1.01)2t. However, this “restarts” the time at 0, whereas really 22.5 years will have passed. We need to shift this function graph 22.5 units (years) to the right, which we can do by subtracting 22.5 from t within the equation. The equation becomes A = 2503.24(1.01)2(t − 22.5), which simplifies to A = 2503.24(1.01)2t − 45. So, the account balance at Cash Cow Bank can be modeled by the function below.
A = 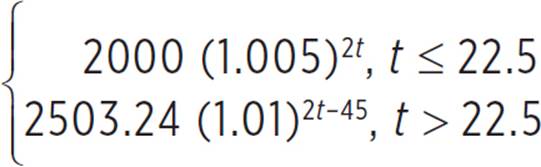
We cannot round
the value of 2t down
to 44, because the
account balance will
not quite have reached
$2,500 at that point.
Let’s graph this piecewise-defined function on the same grid as the Savers Bank account graph, using graphing technology.
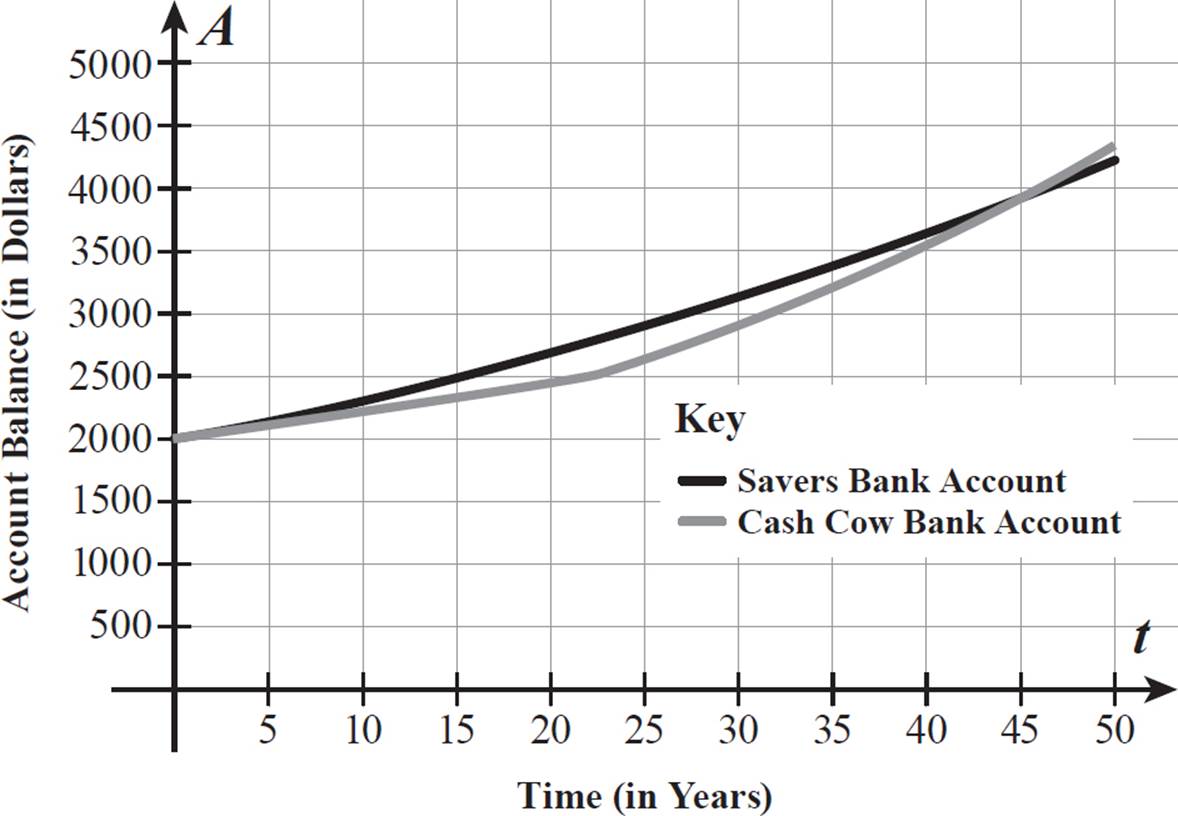
The two function graphs begin at the same point (0, 2000) and appear to intersect when t is approximately equal to 45.5. From t = 0 to t = 45.5, the balance in Savers Bank is greater, and from t = 45.5 to the right, the balance in Cash Cow Bank is greater. So, if Jeremy is going to leave his investment in the bank for any time period up to 45 years, the Savers Bank account will earn him more interest. If he is going to leave his investment in the bank for 46 or more years, the Cash Cow Bank account will earn him more interest.

DRILL
CHAPTER 6 PRACTICE QUESTIONS
Click here to download a PDF of Chapter 6 Practice Questions.
Directions: Complete the following open-ended problems as specified by each question stem. For extra practice after answering each question, try using an alternative method to solve the problem or check your work.
1. Describe the domain, range, end behavior, x-intercept, y-intercept, and point of inflection for the graph of f(x) = −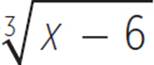 + 2.
+ 2.
2. Graph the function h(x) = |2x| for −1 ≤ x ≤ 2. What is the range for this function?
3. If g(x) = x3 − 5x2 + 3x + 9, what are the x- and y-intercepts of its inverse relation? What is the minimum value of a for which the inverse relation of g(x) with x ≥ a is a cube root function?
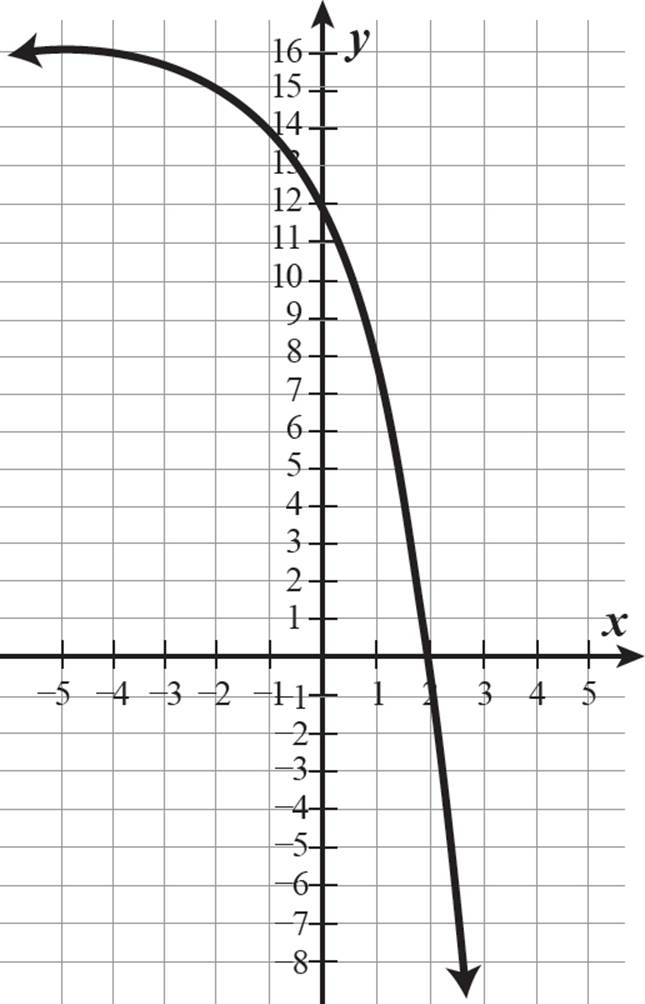
4. Graph the function f(x) = −4 ⋅ 2x + 16.
5. An absolute value function, r(x), has a maximum at (−4, 3) and a left arm with slope 3/2. What equation describes r(x)?
6. Find all solutions to the equation 1/2 x2 − 5 = |x − 1|.
7. At Perry’s Pretzel Parlor, employees are paid a starting hourly wage of $12 for their first year working there. After that, their hourly wage increases by 10% each year, on the anniversary of their date of hire. The employee who has worked at Perry’s Pretzel Parlor the longest has been there for 4 1/2 years. Write a function that gives p(x), an employee’s hourly wage, x years after bring hired at Perry’s Pretzel Parlor, for x-values up to 4.5. What kind of function is this?
8. Naima was riding her skateboard at a constant speed of 0.2 mile per minute along a flat stretch of road. After riding 1.2 miles, she hit a downhill stretch, at which point her distance, d, in miles traveled downhill was given by d = 0.1m2 + 0.4m, where m was the number of minutes since she started going downhill. Write and graph a piecewise-defined function that describes s(x), her total distance traveled, throughout her entire 8-minute ride, where x is the number of minutes since she started the ride.
9. The equation N = A ⋅ ekt represents the continuous exponential decay of a radioisotope, where N represents the remaining quantity after t years, of an original quantity A, and k is a constant specific to a particular radioisotope. If 77% of an original sample of the radioisotope silicon-32 remains after 65 years, what is the half-life of silicon-32? (The half-life is the amount of time it takes half of the original quantity of a substance to decay.)
SOLUTIONS TO CHAPTER 6 PRACTICE QUESTIONS
1. domain: all real numbers; range: all real numbers; end x-intercept: 14; y-intercept: 3.8; point of inflection: (6, 2)
A cube root function always has a domain of all real numbers and a range of all real numbers, so this is the case for f(x). A function in this form is either always increasing or always decreasing. In this case, the coefficient of the cube root is negative (−1), so f(x) is always decreasing. This means that its left arm approaches ∞ and its right arm approaches −∞. Its x-intercept occurs when f(x) = 0.
|
0 = − |
Substitute 0 for f(x). |
|
|
Add |
|
x − 6 = 8 |
Cube both sides. |
|
x = 14 |
Add 6 to both sides. |
The function f(x) = −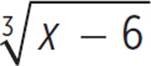 + 2 has an x-intercept of 14.
+ 2 has an x-intercept of 14.
The y-intercept occurs when x = 0.
|
f(0) = − |
Substitute 0 for x. |
|
= − |
Subtract within the radicand. |
|
≈ −(−1.8) + 2 |
Use a calculator to find |
|
≈ 1.8 + 2 |
A negative multiplied by a negative is a positive. |
|
≈ 3.8 |
Add 1.8 + 2. |
The function f(x) = −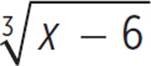 + 2 has a y-intercept of about 3.8.
+ 2 has a y-intercept of about 3.8.
The point of inflection of a function of the form f(x) = a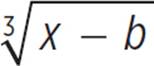 + c is (b, c), so the point of inflection for f(x) = −
+ c is (b, c), so the point of inflection for f(x) = −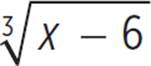 + 2 is (6, 2).
+ 2 is (6, 2).
2. see graph on following page; range: {−2, −1, 0, 1, 2, 3, 4}
The symbol ⌊ ⌋ indicates that this is a floor function, or the greatest integer less than or equal to the value of its argument (2x in this case). When x = −1, 2x = −2, and ë−2û = −2. When x = 0, 2x = 0, and ⌊0⌋ = 0. This is a jump of 2 units, but a floor function for a continuous range of several units should have values at each consecutive integer. The fractional x-value of −1/2 produces an h(x)-value of −1. All x-values greater than −1 and less than −1/2 produce values of 2x that are greater than −2 and less than −1, so they produce h(x)-values of −2.
All x-values greater than or equal to −1/2 and less than 0 produce an h(x)-value of −1. When x = 0, h(x) = 0. When x = 1/2, h(x) = 1. For x-values greater than 0 and less than 1/2, h(x) = 0. This pattern continues, with steps each 1/2 unit long at each integer height, with a closed circle as the left endpoint and an open circle as the right endpoint. The greatest x-value in the domain of h(x) is 2, and h(2) = ⌊2(2)⌋ = 4. The graph of h(x) = ⌊2x⌋ for −1 ≤ x ≤ 2 is shown below.
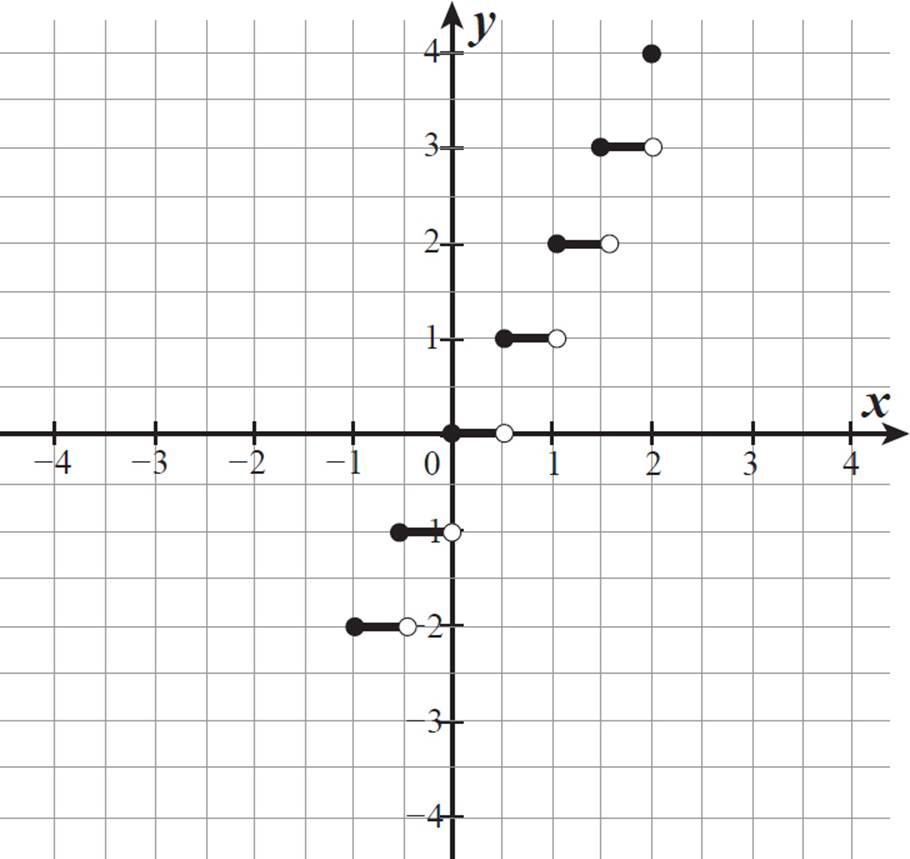
The domain of h(x) was given as −1 ≤ x ≤ 2. The range is each integer from −2 to 4 and does not include any values in between. In other words, the range of h(x) is {−2, −1, 0, 1, 2, 3, 4}.
3. 3
Each coordinate pair (a, b) in a function translates to the point (b, a) in the function’s inverse relation, so any x-intercepts of g(x) translate to y-intercepts of its inverse, and any y-intercepts of g(x) translate to x-intercepts of its inverse.
g(0) = 03 − 5(02) + 3(0) + 9 = 9
The function g(x) has a y-intercept of (0, 9), so its inverse relation has an x-intercept of (9, 0).
To find the x-intercepts of g(x), we must find the x-values that make x3 − 5x2 + 3x + 9 equal to 0. So, we must factor this cubic. According to the Rational Root Theorem, any rational roots of this cubic will be in the set ±{1, 3, 9}. Use the Remainder Theorem to test these potential roots.
g(1) = 13 − 5(12) + 3(1) + 9 = 1 − 5 + 3 + 9 = 8
g(−1) = (−1)3 − 5(−1)2 + 3(−1) + 9 = −1 − 5 − 3 + 9 = 0
g(3) = 33 − 5(32) + 3(3) + 9 = 27 − 45 + 9 + 9 = 0
Both −1 and 3 produced function values of 0, so these are both roots of g(x), and (x + 1) and (x − 3) are factors of x3 − 5x2 + 3x + 9. Multiplied, (x + 1)(x − 3) = x2 − 2x − 3. Divide x3 − 5x2 + 3x + 9 by x2 − 2x − 3 to find the remaining factor.
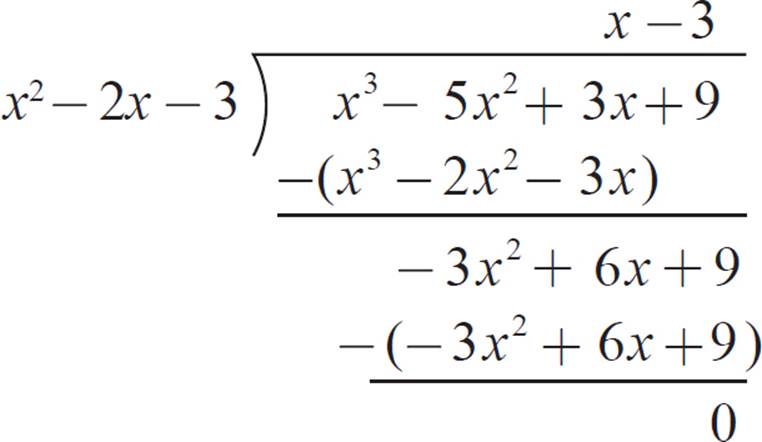
The third factor is (x − 3), so the fully factored form of x3 − 5x2 + 3x + 9 is (x + 1)(x − 3)(x − 3). The function g(x) has x-intercepts of (−1, 0) and (3, 0), so its inverse relation has y-intercepts of (0, −1) and (0, 3).
The root 3 is a repeated root, so g(x) has a local maximum or minimum at (3, 0). The polynomial x3 − 5x2 + 3x + 9 is a cubic with a positive leading coefficient, so the left arm of g(x) points down and the right arm points up. Given the x- and y-intercepts and end behavior, the point (3, 0) is a local minimum of g(x). The graph of g(x) is shown below.
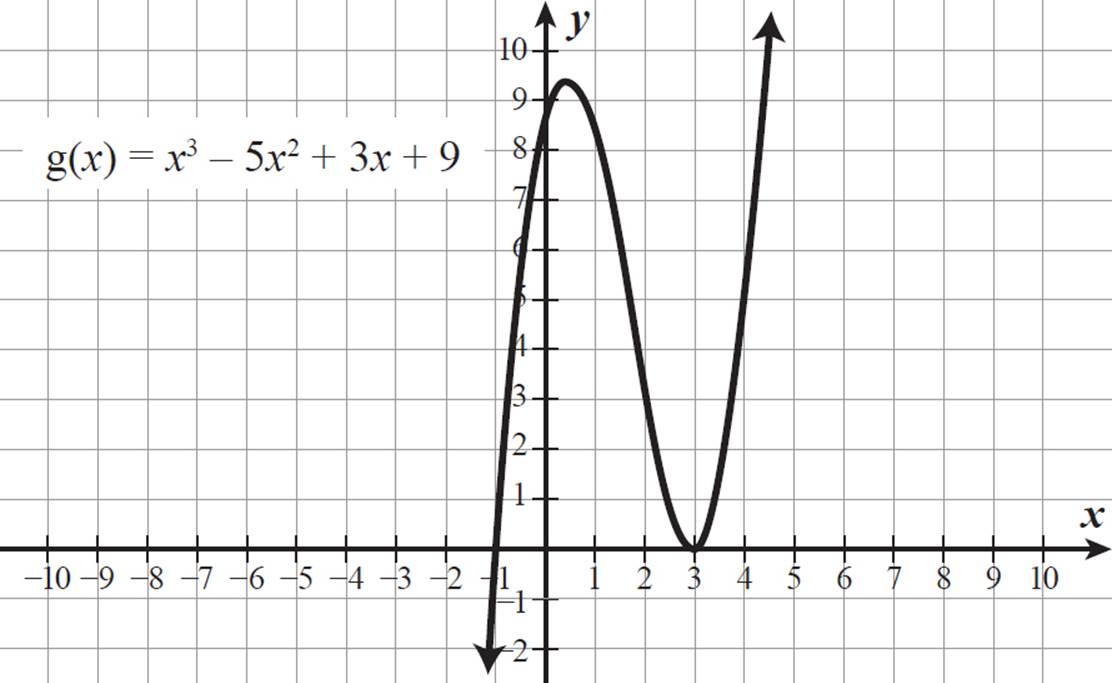
For the inverse relation to be a function, the domain of g(x) must be limited to include a portion of the graph that only increases or only decreases. To find the minimum a-value for which x ≥ a describes this domain restriction, we must find the minimum x-value for the last portion of this graph of g(x), where it is only increasing. This point is the local minimum, (3, 0), because to the right of here, g(x) only increases. For x ≥ 3, g(x) = x3 − 5x2 + 3x + 9 has an inverse relation that is a cube root function.
4. see graph on the following page
As x approaches −∞, −4 ⋅ 2x approaches 0, so f(x) approaches 16. The graph has a horizontal asymptote of 16 for its left arm. The graph is always decreasing, because of the negative coefficient of the exponential term, so the right arm approaches −∞.
When x = 0, f(x) = −4 ⋅ 20 + 16 = 12, so the y-intercept is 12. The x-intercept occurs when f(x) = 0.
|
0 = −4 ⋅ 2x + 16 |
Substitute 0 for f(x). |
|
4 ⋅ 2x = 16 |
Add 4 ⋅ 2x to both sides. |
|
2x = 4 |
Divide both sides by 4. |
|
x = log24 |
Take the logarithm, base 2, of both sides. |
|
x = 2 |
Evaluate log24. |
So, the x-intercept is 2. Find some more points along the graph, using the function equation.
f(−2) = −4 ⋅ 2−2 + 16 = −4 ⋅ 1/4 + 16 = 15
f(−1) = −4 ⋅ 2−1 + 16 = −4 ⋅ 1/2 + 16 = 14
f(1) = −4 ⋅ 21 + 16 = −4 ⋅ 2 + 16 = 8
f(3) = −4 ⋅ 23 + 16 = −4 ⋅ 8 + 16 = −16
So, the graph also passes through (−2, 15), (−1, 14), (1, 8), and (3, −16). The graph of f(x) = −4 ⋅ 2x + 16 is shown below.
5. r(x) = −|3/2 x + 6| + 3
The absolute value function r(x) has a maximum point, so it opens downward, like an upside-down V. This means that the coefficient of the absolute value expression (outside the absolute value expression) must be negative. If the left arm of r(x) has a slope of 3/2, then the right arm has the opposite slope, −3/2.
The maximum value of r(x) is 3. If a downward-opening absolute value function with a maximum of 3 and slopes of 3/2 and −3/2 were centered at the y-axis, it would have an equation of y = −|3/2 x| + 3. However, because r(x) has a maximum at (−4, 3), its line of symmetry is x = −4. To translate y = −|3/2 x| + 3 to the left 4 units, we must add 4 to each x-value.
|
r(x) = −|3/2 (x + 4)| + 3 |
Replace x with (x + 4). |
|
r(x) = −|3/2 x + 6| + 3 |
Distribute the multiplication to both terms within the absolute value. |
Alternatively, you could use the slope and the maximum point to write the equations of the lines that describe each ray of the absolute value function.
For the left ray, use slope 3/2 and point (−4, 3) in the slope-intercept form of a linear equation.
y − 3 = 3/2 (x + 4)
y − 3 = 3/2 x + 6
y = 3/2 x + 9
For the right ray, use slope −3/2 and point (−4, 3).
y − 3 = −3/2 (x + 4)
y − 3 = −3/2 x − 6
y = −3/2 x − 3
Using the second from last line of each equation-writing process, or the fact that the maximum, 3, occurs when the absolute value expression is equal to 0, we can translate these two equations to the absolute value function r(x) = −|3/2 x + 6| + 3.
6. −1 −![]() and 4
and 4
Algebraically solve for the cases where the argument of the absolute value is non-negative and where it is negative, meaning when x − 1 ≥ 0 and when x − 1 < 0.
When x ≥ 1, x − 1 ≥ 0, so |x − 1| = x − 1.
|
1/2 x2 − 5 = x − 1 |
Rewrite the equation with the right side equal to x − 1. |
|
1/2 x2 − x − 4 = 0 |
Subtract x and add 1 to both sides. |
|
x2 − 2x − 8 = 0 |
Multiply both sides by 2. |
|
(x − 4)(x + 2) = 0 |
Factor the quadratic. |
|
x = 4, x = −2 |
Solve for each factor set equal to 0. |
This solution set is for the case where x ≥ 1, so only x = 4 is a solution, while x = −2 is an extraneous solution.
When x < 1, x − 1 < 0, so |x − 1| = −(x − 1), or −x + 1.
|
1/2 x2 − 5 = −x + 1 |
Rewrite the equation with the right side equal to −x + 1. |
|
1/2 x2 + x − 6 = 0 |
Add x and subtract 1 from both sides. |
|
x2 + 2x − 12 = 0 |
Multiply both sides by 2. |
|
x = |
Use the quadratic formula to solve for x. |
|
x = |
Simplify the radicand. |
|
x = |
Rewrite |
|
x = −1 ± |
Divide the numerator by the denominator. |
This solution set is only for x-values less than 1. The value of −1 + ![]() is approximately equal to 2.6, so this is an extraneous solution. The only true solution for this portion of the domain is x = −1 −
is approximately equal to 2.6, so this is an extraneous solution. The only true solution for this portion of the domain is x = −1 − ![]() . The solutions to 1/2 x2 − 5 = |x − 1| are x = 4 and x = −1 −
. The solutions to 1/2 x2 − 5 = |x − 1| are x = 4 and x = −1 − ![]() .
.
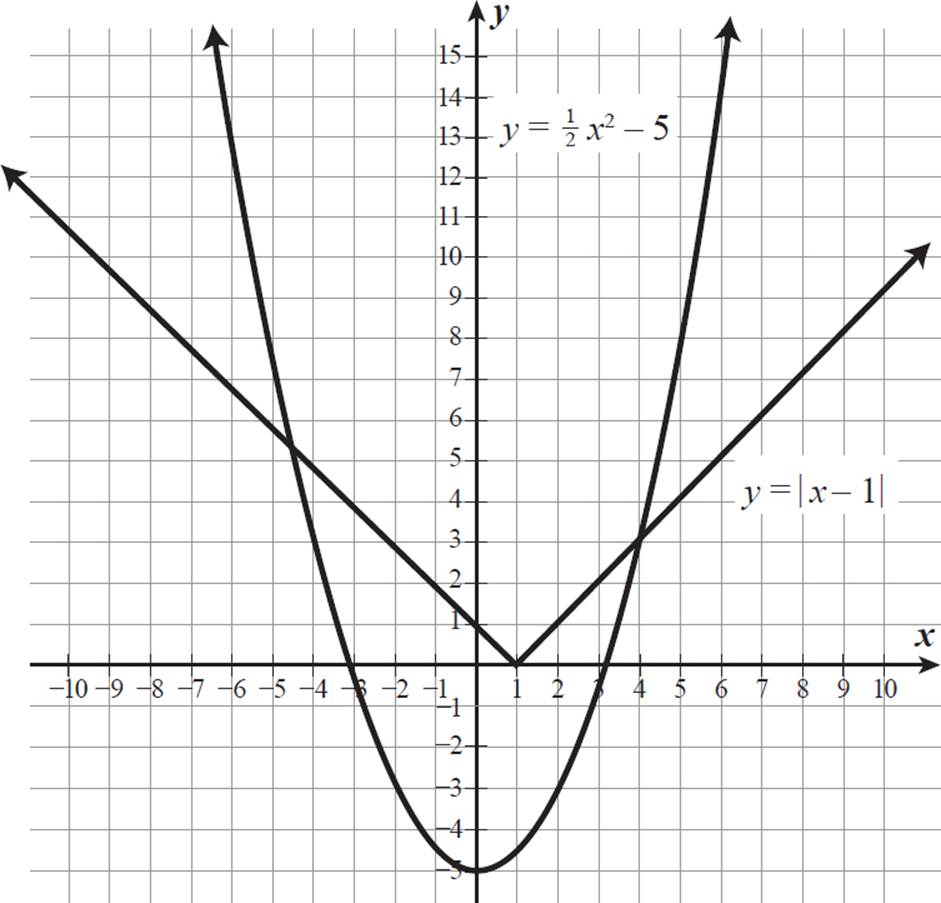
Alternatively, you could graph the functions y = 1/2 x2 − 5 and y = |x − 1|, as shown on the next page. The points of intersection have x-values of 4 and about −4.6 (or −1 − ![]() ), so these are the solutions to the given equation.
), so these are the solutions to the given equation.
7. step function
For the first year, an employee’s hourly wage is $12, so for 0 ≤ x < 1, p(x) = 12. (An employee can only have worked there a minimum of 0 years, so negative x-values do not make sense in this situation.) On the first anniversary of when he or she was hired (when x = 1), the employee’s hourly wage increases by 10%.
12 + 0.1(12) = 13.2
The employee earns $13.20 per hour for his or her second year of work there. Then, when x = 2, the hourly wage increases by 10% again (but 10% of the current amount).
13.2 + 0.1(13.2) = 14.52
On the third anniversary of an employee’s hire date, he or she gets 14.52 + 0.1(14.52) = 15.972 dollars per hour. But, we must round off to the nearest cent: $15.97. On the fourth anniversary of the hire date, the employee gets an hourly wage of 15.97 + 0.1(15.97) = 17.567, which rounds off to $17.57. An employee who was hired 4 1/2 years ago is still earning $17.57 per hour, because the amount will not change again until his or her fifth anniversary of working there. So, the function p(x) can be defined as follows.
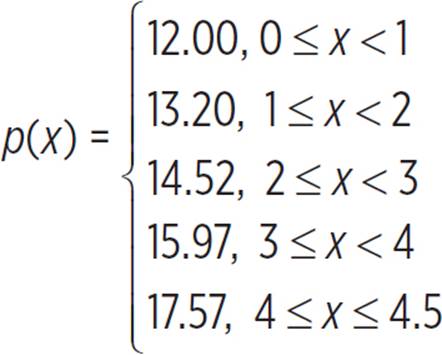
Each section of the graph of p(x) is a horizontal line segment, so this is a step function.
8. see graph below
Along the flat stretch of road, Naima rode at a constant speed of 0.2 mile per minute, so her distance traveled was equal to 0.2x. To write a piecewise-defined function, we need to know at what x-value, or after how many minutes, she hit the downhill. We know she traveled 1.2 miles in this time.
|
1. 2 = 0.2x |
Set distance traveled, 1.2, equal to 0.2x. |
|
6 = x |
Divide both sides by 0.2. |
So, for 0 ≤ x ≤ 6, Naima’s distance traveled was given by the function s(x) = 0.2x. After 6 minutes, her distance traveled downhill was given by d = 0.1m2 + 0.4m, where m was the number of minutes since she started going downhill. Notice that m is different fromx, the number of minutes since Naima began her ride. Because m = 0 when x = 6, and all x-values will be 6 minutes more than all m-values, we can say that x = m + 6, or m = x − 6. Also, d is different from s(x). When d = 0, s(x) = 1.2, and all s(x)-values will be 1.2 miles greater than all d-values, so s(x) = d + 1.2.
|
s(x) = 0.1m2 + 0.4m + 1.2 |
Substitute (0.1m2 + 0.4m) for d. |
|
s(x) = 0.1(x − 6)2 + 0.4(x − 6) + 1.2 |
Substitute (x − 6) for m. |
|
s(x) = 0.1(x2 − 12x + 36) + 0.4(x − 6) + 1.2 |
Expand the squared binomial. |
|
s(x) = 0.1x2 − 1.2x + 3.6 + 0.4x − 2.4 + 1.2 |
Use the distributive property. |
|
s(x) = 0.1x2 − 0.8x + 2.4 |
Combine all like terms. |
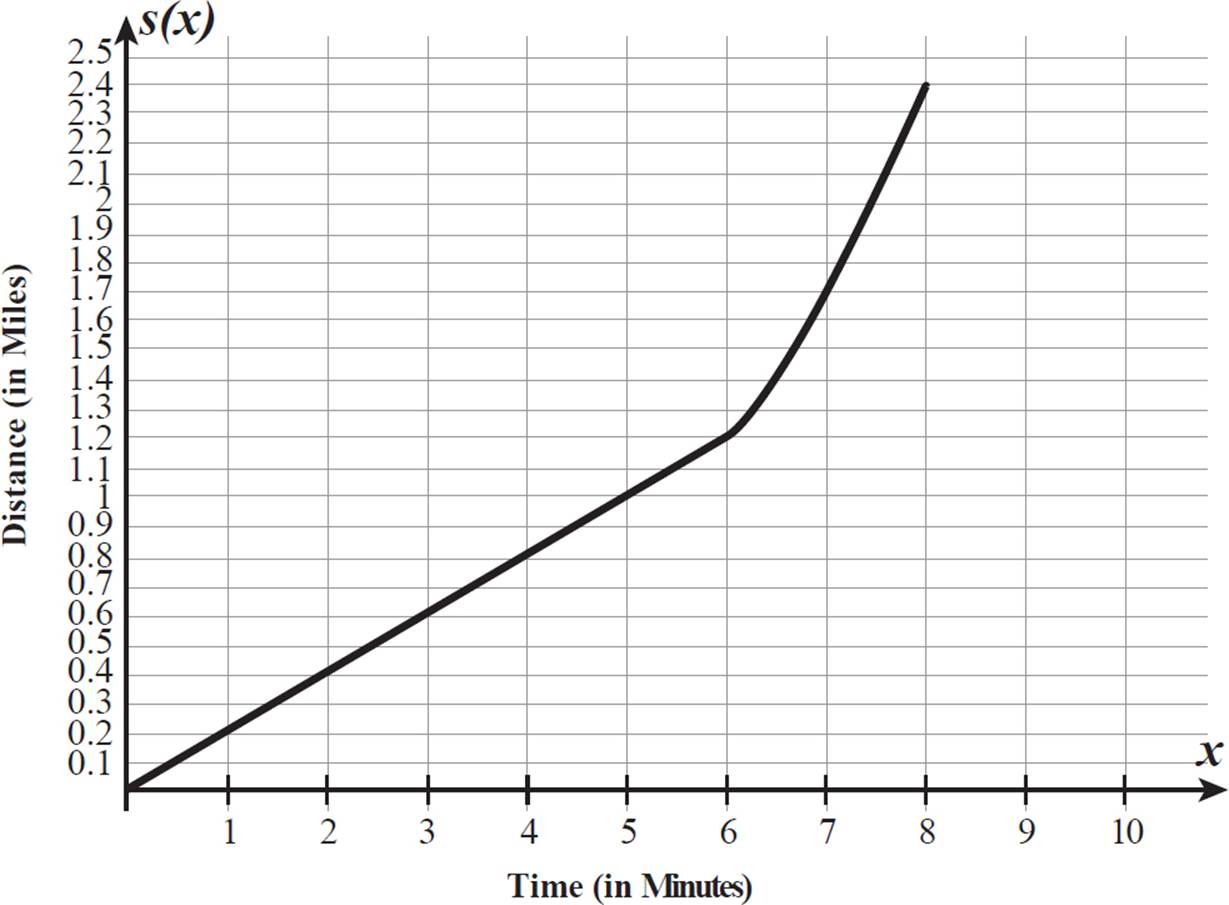
This equation describes s(x) only for times 6 minutes or more into Naima’s ride. Her ride was a total of 8 minutes long. So, her total distance traveled throughout this ride is given by the piecewise-defined function below.
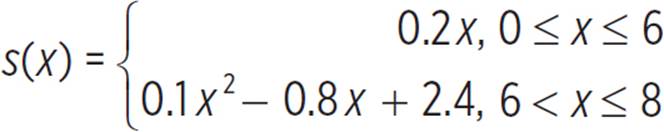
To graph this, we draw a straight line segment along y = 0.2x from (0, 0) to (6, 1.2) and draw the quadratic using points along it, starting at (6, 1.2). (Notice that 0.1(62) − 0.8(6) + 2.4 is also equal to 1.2, so the function is continuous.)
s(7) = 0.1(72) − 0.8(7) + 2.4 = 4.9 − 5.6 + 2.4 = 1.7
s(8) = 0.1(82) − 0.8(8) + 2.4 = 6.4 − 6.4 + 2.4 = 2.4
The quadratic goes from (6, 1.2) through (7, 1.7) and to (8, 2.4). The graph of s(x) is shown below.
9. 173 years
If 77% of the original sample quantity remains, then the ratio of the remaining quantity to the original quantity (or N/A) is equal to 0.77.
|
N/A = ekt |
Divide both sides of N = A ⋅ ekt by A, to get N/A on the left side. |
|
0. 77 = e65k |
Substitute 0.77 for N/A and 65 for t. |
|
ln0.77 = 65k |
Take the ln of both sides. |
|
|
Divide both sides by 65. |
|
k ≈ −0.004 |
Use your calculator to find the value of |
So, the exponential decay of silicon-32 is given by the equation N = A ⋅ e−0.004t. This can also be written as N/A = e−0.004t. To find the half-life of silicon-32, substitute 1/2, or 0.5, for N/A.
|
0. 5 = e−0.004t |
|
|
ln0.5 = −0.004t |
Take the ln of both sides. |
|
|
Divide both sides by −0.004. |
|
t ≈ 173 |
Use your calculator to find the value of |
The half-life of silicon-32 is about 173 years.
REFLECT
Congratulations on completing Chapter 6! Here’s what we just covered. Rate your confidence in your ability to
• Graph cube root functions
1 2 3 4 5
• Graph piecewise-defined functions, including step functions (such as floor and ceiling functions) and absolute value functions
1 2 3 4 5
• Solve single-variable absolute value equations, both algebraically and by graphing systems of equations
1 2 3 4 5
• Graph exponential functions
1 2 3 4 5
• Write and use cube root, piecewise-defined, and exponential functions to represent real-life situations and solve problems
1 2 3 4 5
If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.
 Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.
Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.
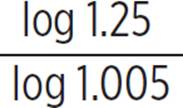 = 2t
= 2t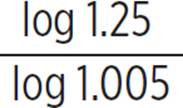 .
.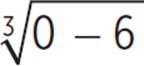 + 2
+ 2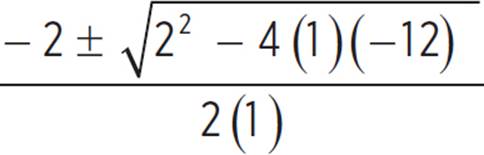
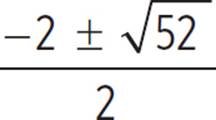
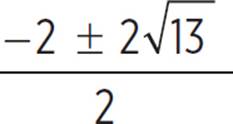
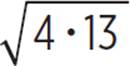 , which simplifies as 2
, which simplifies as 2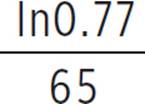 = k
= k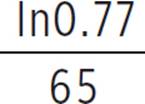 and round off.
and round off.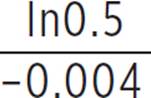 = t
= t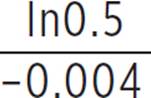 and round off.
and round off.