High School Algebra II Unlocked (2016)
Chapter 1. Complex Numbers and Polynomials
Lesson 1.5. Tips for Factoring Polynomials
REVIEW
QUADRATIC FORMULA:
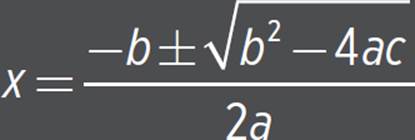
for a quadratic equation of the form ax2 + bx + c = 0
Much of the art of factoring is in recognizing familiar patterns. For example, a good way to start is by looking for a common factor in all terms. Next, check to see if the polynomial matches any of the common polynomial identities.
In some cases, only part of a given polynomial may need to be factored.

Which of the following is equivalent to x12 − 14x6 + 52?
A. (x6 − ![]() x3)2 + 52
x3)2 + 52
B. (x4 − 7x2)3 + 52
C. (x6 − 7)2 + 3
D. (x2 − 7)6 + 3
The exponents are very large, which makes this appear difficult to rewrite, but it’s actually fairly simple once you see the relationship between the exponents. Notice that x12 is the same as (x6)2. This allows us to rewrite the expression in terms of x6, as (x6)2 − 14x6 + 52. We can even let a = x6, which makes the expression a2 − 14a + 52. Now it seems more manageable!
There are no integer factors of 52 that add up to −14, so we can’t factor the entire expression using FOIL. However, we don’t need to factor the entire polynomial. The answer choices show a factorization of only part of the polynomial. Notice that they each include a squared binomial.
We can use a2 − 14a to write a squared binomial, with the number 52 broken up to accommodate that. The polynomial identity for the square of a difference is (a − b)2 = a2 − 2ab + b2. If we view a2 − 14a as a2 − 2ab, then 14 = 2b and b = 7. So, (a − 7)2 = a2 − 14a + 49. Rewrite the original expression to include this trinomial.
|
a2 − 14a + 52 = a2 − 14a + 49 + 3 |
Rewrite the expression, showing 52 as the sum of 49 and 3. |
|
= (a − 7)2 + 3 |
Substitute (a − 7)2 for a2 − 14a + 49. |
|
= (x6 − 7)2 + 3 |
Substitute x6 for a. |
The correct answer is (C).

This method is called
completing the square,
and it’s the same method
we use to rewrite quadratic
functions in vertex form
(see Example 13).
To check our work, let’s expand the expression (x6 − 7)2 + 3 to make sure it is equivalent to x12 − 14x6 + 52.
|
(x6 − 7)2 + 3 = (x6)2 − 2(x6)(7) + 72 + 3 |
Expand the squared binomial using the polynomial identity (a − b)2 = a2 − 2ab + b2. |
|
= x12 − 14x6 + 49 + 3 |
Evaluate exponents and products. |
|
= x12 − 14x6 + 52 |
Combine like terms. |
You could also expand
using FOIL, just in case
you have misremembered
the identity used here.

Although you may sometimes be expected to factor only part of a polynomial, as in Example 17, you will usually need to factor the entire polynomial, as when solving for zeros of a function.
The act of factoring a polynomial is essentially dividing the polynomial by one factor and writing the quotient as the other factor. In order for this to work, the factor must divide evenly into the original polynomial, with no remainder.
The Remainder Theorem states that when a polynomial p(x) is divided by (x − a), the remainder is p(a), so p(a) is equal to 0 if and only if (x − a) is a factor of p(x).
This can help us confirm a root if we’re having trouble factoring a polynomial.
In Example 15, if we didn’t see the common factor of −3x, we might have felt stuck in our efforts to factor the cubic −3x3 − 9x2 + 30x. But, in that case, we could have tested various values as our guesses for possible zeros, using the Remainder Theorem. For example, let’s test 0, 1, and 2.
p(x) = −3x3 − 9x2 + 30x
p(0) = −3(03) − 9(02) + 30(0) = 0 + 0 + 0 = 0
Because p(0) = 0, we know that (x − 0), or x, is a factor of −3x3 − 9x2 + 30x, according to the Remainder Theorem.
p(1) = −3(13) − 9(12) + 30(1) = −3 − 9 + 30 = 18
Because p(1) is not equal to 0, we know that (x − 1) is not a factor.
p(2) = −3(23) − 9(22) + 30(2) = −24 − 36 + 60 = 0
Because p(2) = 0, we know that (x − 2) is a factor.
So far, we know that x and (x − 2) are both factors of −3x3 − 9x2 + 30x. If we also recognize that −3 can be factored out, we can work out the following:
|
−3x3 − 9x2 + 30x |
= −3(x3 + 3x2 −10x) |
Factor out −3. |
|
= −3x(x2 + 3x − 10) |
Factor out x. |
|
|
= −3x(x − 2)(_____) |
Factor out (x − 2). |
At this point, we should be able to recognize that the other factor is (x + 5). However, even if we still don’t see it, we can fall back on the good old quadratic formula.
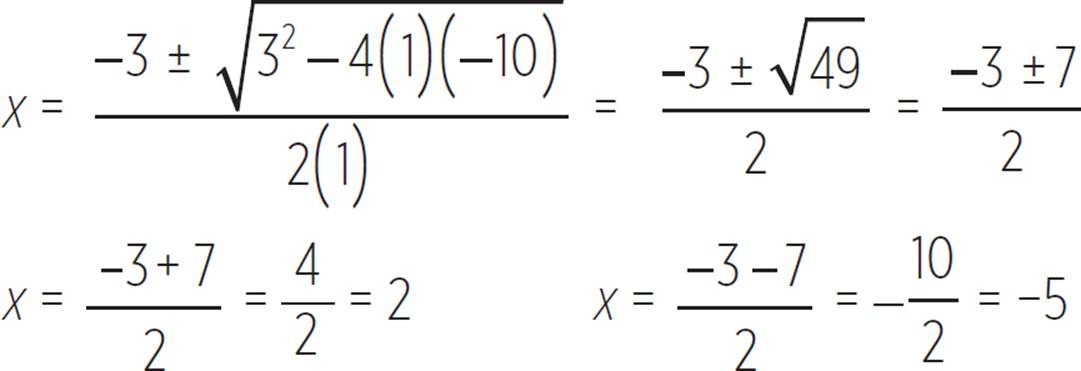

Here is how you may see polynomial factoring on the SAT.
Which of the following represents all zeros of the function f(x) = 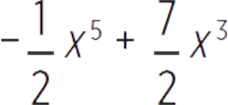 + 9x?
+ 9x?
A) 3 only
B) −3, 3
C) −3, 0, 3
D) −3, 0, 2, 3
We had already found the root 2, so this work with the quadratic formula gave us the other root, −5. The full factorization of the polynomial is −3x(x − 2)(x + 5).
Almost any time you
are expected to factor a
higher-degree polynomial
on a math test, the roots
will be rational numbers.
The Remainder Theorem provides us with a way to test potential roots in the given polynomial, but sometimes we need help with the first step of figuring out what roots to test. The Rational Root Theorem provides a set of potential roots, narrowing down our choices from any possible rational numbers to a smaller number of possibilities.
The Rational Root Theorem states that if a polynomial has any rational roots, they must be in the form ±  .
.
If we were trying to find the roots of x4 − x3 − 12x2 − 4x + 16, we would know that any rational roots would be a positive or negative ratio of a factor of 16 (the constant term) to a factor of 1 (the coefficient of x4). Factors of 16 include 1, 2, 4, 8, and 16. Factors of 1 include…just 1. So, any rational roots of x4 − x3 − 12x2 − 4x + 16 must be in the set {± 1/1, ± 2/1, ± 4/1, ± 8/1, ± 16/1}, or {−16, −8, −4, −2, −1, 1, 2, 4, 8, 16}. Indeed, the roots are −2 (repeated), 1, and 4, as you saw in Example 16.

Factor 2x3 − x2 − 7x + 6.
Let’s start by using the Rational Root Theorem. Any rational roots of this polynomial will be in the set of ± 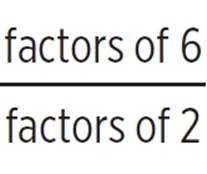 , or ±
, or ± 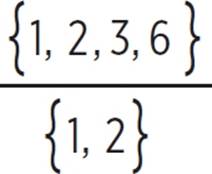 . These possible roots include ±{1, 2, 3, 6, 1/2, 3/2}.
. These possible roots include ±{1, 2, 3, 6, 1/2, 3/2}.
We can use the Remainder Theorem to test any of these roots. Let’s test 1.
p(x) = 2x3 − x2 − 7x + 6
p(1) = 2(13) − 12 − 7(1) + 6 = 2 − 1 − 7 + 6 = 0
Because p(1) = 0, (x − 1) is one factor of the polynomial.
Because 2 is the leading coefficient and is not a common factor of all terms, it’s likely that one of the roots is ± 1/2 or ± 3/2. Let’s use the Remainder Theorem again.
Notice that 2/2 simplifies
to 1, which is the same as
1/1, and 6/2 simplifies
to 3, which is the same
as 3/1. That’s why our
set of 8 potential roots
turned out to be only 6
distinct potential roots.
|
p(1/2) |
= 2(1/2)3 − (1/2)2 − 7(1/2) + 6 |
|
|
= 1/4 − 1/4 − 7/2 + 6 |
||
|
= 5/2 |
Not a root |
|
|
p(−1/2) |
= 2(−1/2)3 − (−1/2)2 − 7(−1/2) + 6 |
|
|
= −1/4 − 1/4 + 7/2 + 6 |
||
|
= 9 |
Not a root |
|
|
p(3/2) |
= 2(3/2)3 − (3/2)2 − 7(3/2) + 6 |
|
|
= 27/4 − 9/4 − 21/2 + 6 |
||
|
= 9/2 − 21/2 + 6 |
||
|
= 0 |
Aha! 3/2 is a root, so (2x − 3) is one factor of the polynomial. So far we have (x − 1)(2x − 3), which expands to 2x2 − 5x +3. We need one more factor to complete 2x3 − x2 − 7x + 6. At this point, we can just divide as we would with numbers, in long-division form. We know that the polynomial 2x2 − 5x + 3 must be multiplied by x to get a beginning of 2x3.
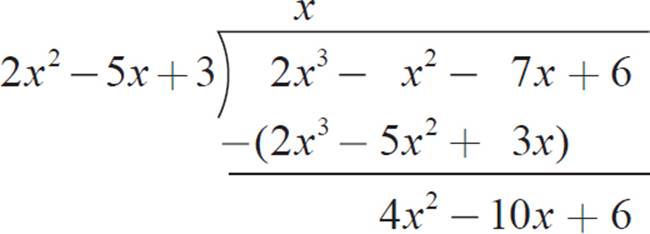
Sure, you could write the
factor (x − 3/2) based
on the root 3/2, but then
you’d have to later multiply
by 2. The factor (2x − 3)
also corresponds to a
root of 3/2 but doesn’t
include any fractions
to complicate things.
The difference between 2x3 − x2 − 7x + 6 and 2x3 − 5x2 + 3x is 4x2 − 10x + 6. It looks like we should now multiply 2x2 − 5x + 3 by 2.
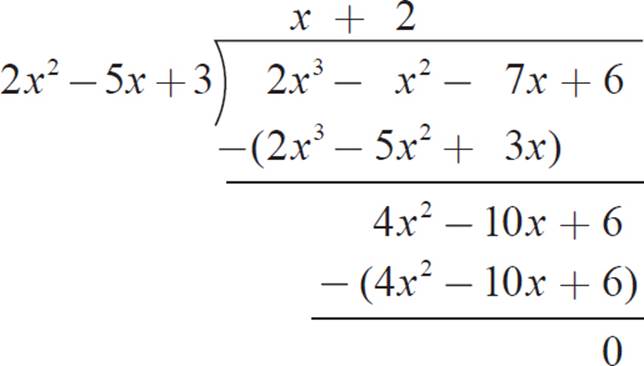

We need to factor the polynomial to find the zeros of the function.
|
−1/2 (x5 − 7x3 − 18x) |
Factor out −1/2. |
|
−1/2 x(x4 − 7x2 − 18) |
Factor out the common factor, x. |
|
−1/2 x[(x2)2 − 7(x2) − 18] |
See the trinomial in the form a2 − 7a − 18. |
|
−1/2 x(x2 − 9)(x2 + 2) |
Factor the trinomial as (a − 9)(a + 2). |
|
−1/2 x(x + 3)(x − 3)(x2 + 2) |
Factor the difference of squares, x2 − 9. |
The expression x2 + 2 cannot be further factored using real numbers, and it does not correspond to any x-intercepts, or real zeros, of the function. Set each of the other factors equal to 0 to solve for the real zeros of f(x).
|
−1/2 x = 0 |
x + 3 = 0 |
x − 3 = 0 |
|
x = 0 |
x = −3 |
x = 3 |
The real zeros of f(x) are −3, 0, and 3. The correct answer is (C).
There is no remainder from our division, so (x + 2)(2x2 − 5x + 3) = 2x3 − x2 − 7x + 6. The polynomial 2x3 − x2 − 7x + 6 = (x − 1)(2x − 3)(x + 2), fully factored.
Alternatively, we could have continued testing other potential roots using the Remainder Theorem. We eventually would have found that p(−2) = 2(−2)3 − (−2)2 − 7(−2) + 6 = −16 − 4 + 14 + 6 = 0, which would have told us that (x + 2) was a factor.

Polynomials with Complex Roots
What about a polynomial like x2 + 9? According to the Rational Root Theorem, any rational roots would be in the set ±{1, 3, 9}, but all six of those numbers fail the Remainder Theorem test. For example, (−3)2 + 9 = 9 + 9 = 18, not 0. None of these six potential rational roots is a root of x2 + 9. The graph of y = x2 + 9 never crosses the x-axis, and the function has no real zeros.
Even though there are no real roots of x2 + 9, there are imaginary roots! Remember i ? If x = 3i, then x2 + 9 = 0, because (3i)2 + 9 = 9i2 + 9 = 9(−1) + 9 = −9 + 9 = 0. Actually, there is one more imaginary-number solution to this equation. To solve x2 + 9 = 0, we should factor x2 + 9 as a difference of squares, x2 − (−9), where −9 is the value of (3i)2. So, (x + 3i)(x − 3i) = 0, and −3i and 3i are the complex-number solutions for x.
Other polynomial identities can also be applied to complex number situations, as long as we are careful to remember that i2 = −1.
A polynomial with real
coefficients will only
have complex number
roots in conjugate pairs,
for complex numbers
that include imaginary
components. In other
words, if one root of a
polynomial with real
coefficients is of the
form a + bi, with b ≠ 0,
then a − bi is also a root
of the polynomial.

Find all solutions to the equation 2x4 − 30x2 = 32.
|
2x4 − 30x2 − 32 = 0 |
Move all terms to one side. |
|
2(x4 − 15x2 − 16) = 0 |
Factor out 2. |
|
2[(x2)2 − 15(x2) − 16] = 0 |
Recognize that the trinomial is in the form a2 − 15a − 16. |
|
2(x2 − 16)(x2 + 1) = 0 |
Factor the trinomial as (a − 16)(a + 1). |
|
2(x + 4)(x − 4)(x + i)(x − i) |
Factor differences of squares, both real and imaginary. |
|
x = −4, x = 4, x = −i, x = i |
Solve each factor set equal to 0. |
The solutions to the equation 2x4 − 30x2 = 32 are x = ±4 and x = ±i.

For example, the square of
a binomial identity,
(a + b)2 = a2 + 2ab + b2,
can be applied to complex
numbers: (a + bi)2 =
a2 + 2abi + b2i2, so
(a + bi)2 = a2 + 2abi − b2.
Also, FOIL becomes
(a + bi)(c + di) =
ac + (ad + bc)i − bd.
The fact that i2 = −1
produces a negative final
term in both cases.
If we were only looking for the real solutions to this equation, we could graph the function y = 2x4 − 30x2 − 32 and find its x-intercepts, where y = 0. For this function, we will need to adjust the scale on our graphing calculator or program, to see how the function behaves below the x-axis. The graph of y = 2x4 − 30x2 − 32 is shown below.
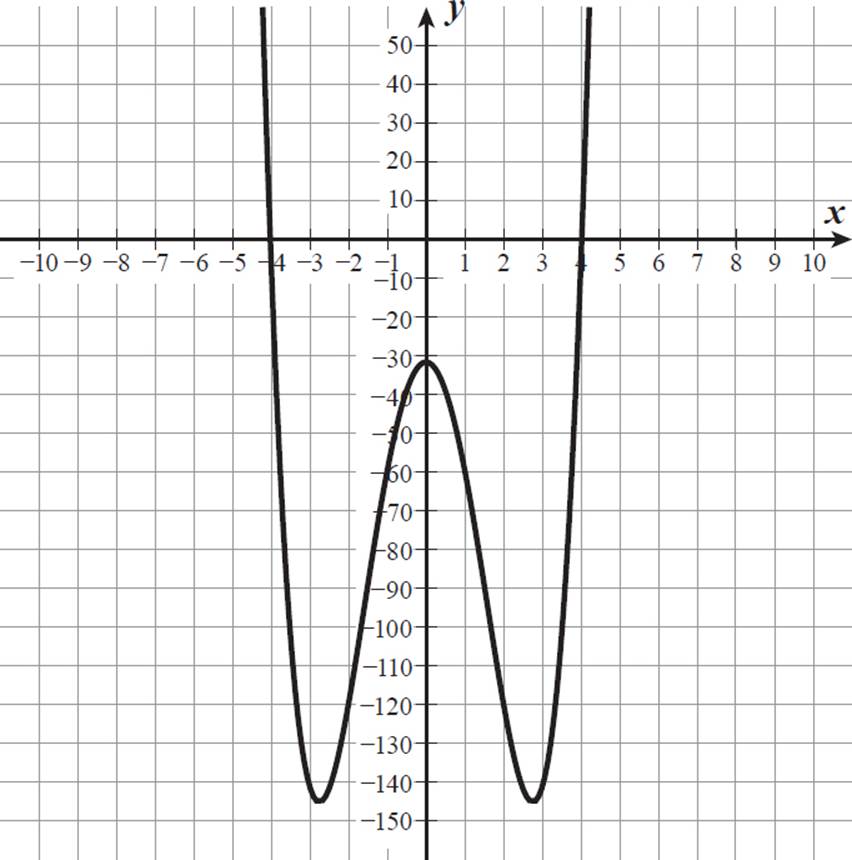
The only two x-intercepts are at −4 and 4, and neither is at a turning point, so −4 and 4 are the only two real solutions to the given equation. With three turning points and both ends pointing up, the graph must represent a polynomial of at least degree 4, which indicates that there are additional solutions, but the graph does not indicate what those additional solutions are. To find the imaginary-number solutions, we need to solve the equation algebraically, as shown on the previous page.


Find all solutions to the equation 3x2 − 6x = −5.
We can rewrite this equation as 3x2 − 6x + 5 = 0. However, it does not seem to be factorable, so we must use the quadratic formula.
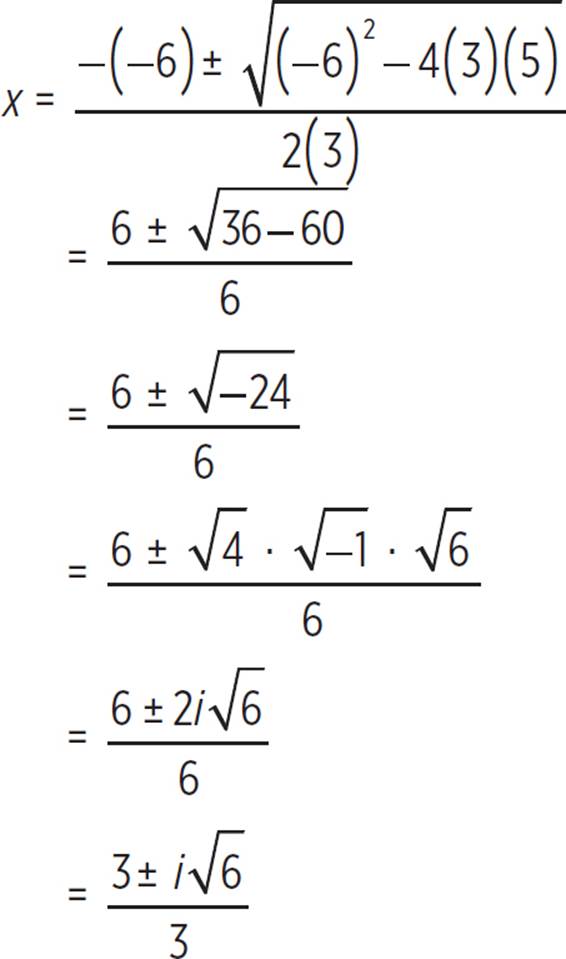
If you graph this quadratic,
either by hand or using
graphing technology, you
will see that the parabola
does not cross the x-axis.
That means that the
equation has no real-
number solutions. Both
solutions must include
imaginary numbers.
The solutions to 3x2 − 6x = −5 are x = 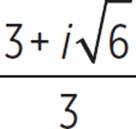 and x =
and x = 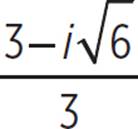 . These roots can also be written as 1 +
. These roots can also be written as 1 + 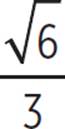 i and 1 −
i and 1 − 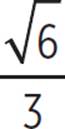 i, in the standard form for complex numbers.
i, in the standard form for complex numbers.
