Idiot's Guides: Algebra I (2015)
Part IV. Polynomials
Chapter 12. Multiplying and Dividing Polynomials
In This Chapter
· Multiplying a monomial by a polynomial using the distributive property
· Multiplying two binomials using the FOIL rule
· Multiplying larger polynomials in vertical format
· Dividing by a monomial
· Polynomial long division
In the last chapter, we looked at how polynomials could fit into our understanding of addition and subtraction. Now it’s time to revisit multiplication and division. We need to see what ideas we’ve already learned that are still useful, and what modifications we might need to make. In this chapter, we’ll review methods of multiplication we learned earlier that will still be useful, examine some special cases, and explore what division is possible when working with polynomials.
Multiplying Polynomials
To multiply two polynomials, you’ll employ some methods you’ve already learned. Because each monomial involves a power of the variable, the rule for multiplying powers of the same base will be key. You’ll also use the distributive property and the FOIL rule.
To multiply two monomials, like (5x3)·(−8x2), you multiply coefficient by coefficient and variable by variable. Because each of the variables is raised to a power, you need to use the rule for exponents, and add the exponents.
(5x3)·(−8x2) = 5 · (−8)·(x3 · x2) = −40x3 + 2 = −40x5
If one of the monomial factors is a constant, multiply the coefficients, and the variable factor is unchanged.
(−7)·(4t7) = (−7)·(4)·(t7) = − 28t7
If one (or both) of the factors is a first degree monomial, remember that you can write in the exponent of 1 that usually isn’t shown, and then apply the exponent rule.
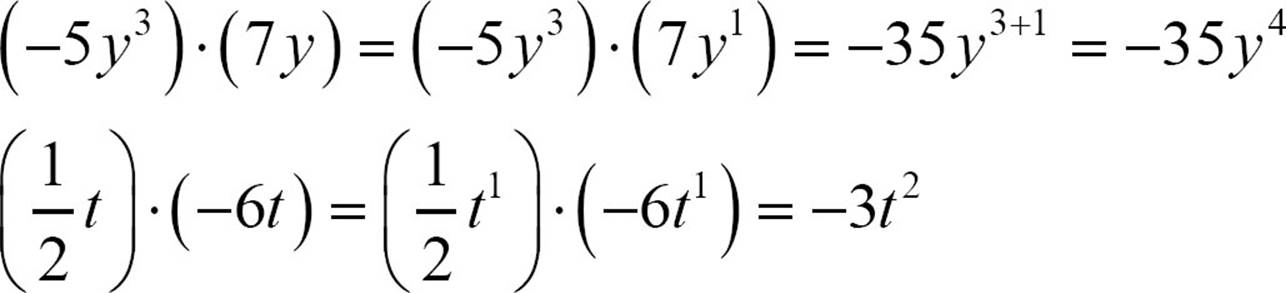
Multiplying one monomial by one monomial is the basis of all polynomial multiplication. Each of the methods that we’ll explore breaks problems down to a collection of small multiplications. Let’s take what we know about multiplying monomials and build to larger problems.
Review of Distributive Property
To multiply a single monomial by a larger polynomial, we’re going to turn to our old friend, the distributive property. You’ve used the distributive property before. It states that multiplying a single term by a sum of terms is equivalent to multiplying that one term by each of the terms in the sum. Applying that to polynomials results in a problem like this one.
3x2 (5x3 − 7x2 + 2x − 6) = (3x2)(5x3) + (3x2)(−7x2) + (3x2) (2x) + (3x2) (−6)
= 15x5 − 21x4 + 6x3 − 18x2
The distributive property lets you change the problem into a collection of multiplications, all monomial multiplied by monomial. Follow the same rules for those as you have before. Multiply the coefficients and multiply the powers of the variable by keeping the variable and adding the exponents. The distributive property says you can add like terms after multiplying, but if the polynomials were properly simplified before you started, there shouldn’t be any like terms to combine.
THINK ABOUT IT
When you multiply a polynomial by a monomial using the distributive property, each term of the polynomial is multiplied by the monomial. Each of the terms in the polynomial was a different power of the variable, and each was multiplied by the same term. The power of each term was increased by the same amount so the terms of the product will all be distinct powers of the variable, and no combining will be necessary.
You might encounter a larger problem, involving a multiplication as well as other operations, or more than one multiplication, in which you will have simplifying to do at the end. The following example has two different multiplications.
4t (8t2 + 3t + 4) − 7t2 (t2 − 5t + 2)
The first multiplication, 4t(8t2 + 3t + 4), is a monomial multiplied by a trinomial. The trinomial is in simplest form, so after that multiplication, there won’t be any like terms.
4t (8t2 + 3t + 4) = 32t3 + 12t2 + 16t
The second multiplication, −7t2 (t2 − 5t + 2), is also a monomial times a trinomial, with the trinomial in simplest form, so that product has no like terms.
−7t2 (t2 − 5t + 2) = −7t4 + 35t3 − 14t2
When the whole problem gets put together, however, there are terms from the first multiplication that you can combine with terms from the second.
4t (8t2 + 3t + 4) − 7t2 (t2 − 5t + 2)
32t3 + 12t2 + 16t − 7t4 + 35t3 − 14t2
− 7t4 + (32t3 + 35t3) + (12t2 − 14t2) + 16t
− 7t4 + 67t3 − 2t2 + 16t
CHECK POINT
Complete each multiplication using the distributive property.
1. 5a (2a2 + 3a)
2. −3b2 (2b2 − 3b + 5)
3. 2x2 (11x2 − 3x − 7)
4. −3x3 (2 + 4x − 5x2)
5. 3y4 (2y6 − y2)
6. 8x (x2 − 3)
7. −5a3 (2a4 − 4a2 + 6)
8. 7x5 (9 − 3x3)
9. −6x4 (x2 + x + 3)
10. −x3 (x5 − x4 + x3 − x2 + x − 1)
The other technique that’s already part of your toolbox and is a crucial skill for multiplying polynomials is the FOIL rule. It’s useful in only one situation, the multiplication of two binomials, but that’s a very common event. Multiplying two terms by two terms requires four separate multiplications that are designated as First, Outer, Inner, and Last.
Review of FOIL
The FOIL rule states that (a + b)(c + d) = ac + ad + bc + bd but writing it in that form doesn’t really communicate it very well. Let’s try this instead. Every binomial is made up of two monomials. Call them the First and the Last, so in the binomial 5x2 + 3x, 5x2 is the First and 3x is the Last. In the binomial 2x3 − 7x2, 2x3 is the First and −7x2 is the Last.
When you multiply (5x2 + 3x)(2x3 − 7x2), you have (First + Last)(First + Last). You want to multiply First × First and Last × Last, but you also want to multiply Firsts and Lasts together. There’s a First × Last pair on the outer ends and a Last × First pair in the middle.
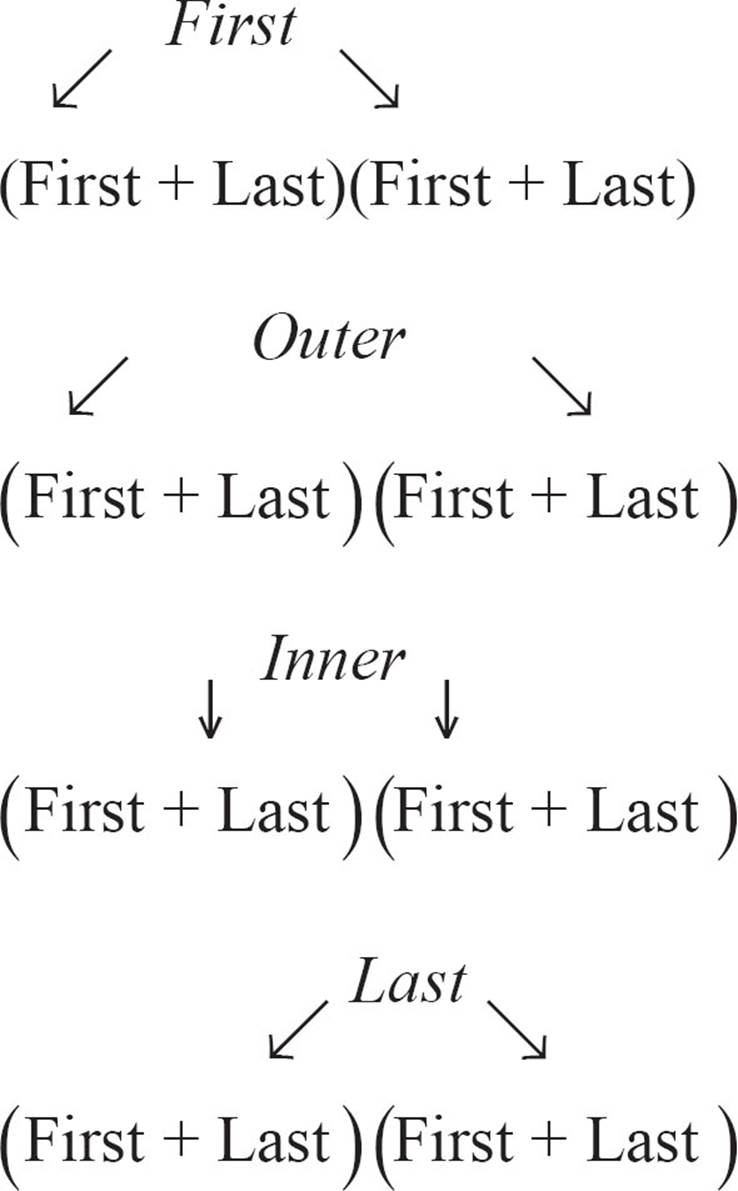
When all the multiplications are done, there may (or may not) be like terms that can be combined. Our earlier example will have like terms.
(5x2 + 3x)(2x3 − 7x2) = 5x2 · 2x3 + 5x2 (– 7x2) + 3x · 2x3 + 3x (– 7x2)
= 10x5 − 35x4 + 6x4 − 21x3
= 10x5 − 29x4 − 21x3
Here’s an example of the multiplication of two binomials that doesn’t have any like terms after the multiplication is done.
(x2 + 3) (2x + 4) = x2 · 2x + x2 · 4 + 3 · 2x + 2 · 4
= 2x3 + 4x2 + 6x + 8
The FOIL rule is most often used for multiplying two first-degree binomials to produce a second-degree trinomial. When you multiply (x + 5)(x + 2), you get a trinomial beginning with x2.
(x + 5) (x + 2) = x·x + 2 · x + 5 ·x + 5 · 2
= x2 + 2x + 5x + 10
= x2 + 7x + 10
The product of 3x − 7 and −4x + 1 is also a second degree trinomial.
(3x − 7) (−4x + 1) = 3x (− 4x) + 3x · 1 + (−7) (−4x) + (−7) · 1
= −12 x2 + 3x + 28x − 7
= −12 x2 + 31x − 7
CHECK POINT
Complete each multiplication using the FOIL rule.
11. (y + 6)(y − 1)
12. (x + 5)(x + 2)
13. (t − 3)(t − 2)
14. (b − 4)(b + 6)
15. (y + 3)(3y − 1)
16. (3x − 8) (4x + 5)
17. (3x + 1)(2x − 3)
18. (2x − 7)(4x + 9)
19. (10a − 3) (8a − 5)
20. (x2 + 9)(x2 − 4)
Special Products
The FOIL rule can handle any product of two binomials, but two common patterns are worth pointing out. One occurs when you multiply a binomial by itself, squaring it, and the other when you multiply the difference of two monomials by their sum.
When you square a binomial, the product is a trinomial. Two of the terms of that trinomial are the squares of each term of the binomial, and the third is twice the product of the two terms. Let’s start with a simple example.
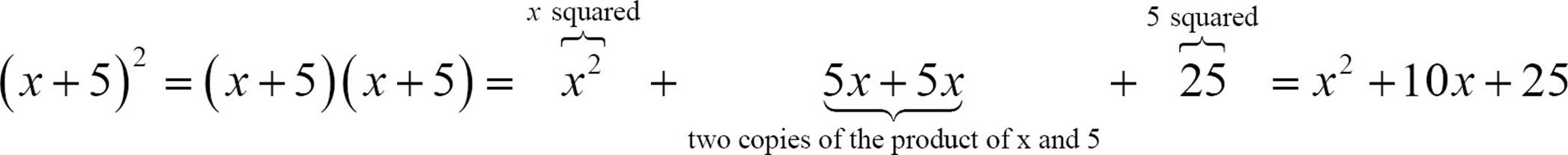
ALGEBRA TRAP
When squaring a binomial, many people will forget the FOIL rule and just square each term. Don’t be one of them. One of the reasons you learn the pattern of the perfect square is so that you won’t make that mistake. Each term of the first binomial must be multiplied by both terms of the second. (a + b)2 ≠ a2 + b2
Recognizing this pattern lets you square binomials quickly. (t + 7)2 = t2 + 2(7t) + 72 = t2 + 14t + 49 or (y − 3)2 = y2 + 2(−3y) + (−3)2 = y2 − 6y + 9. The same rule applies for more complicated binomials.
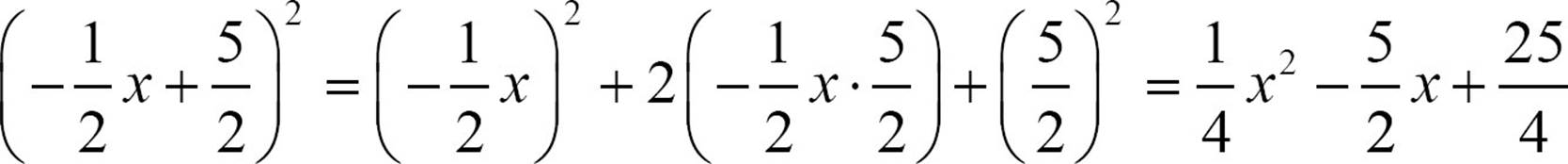
When you multiply a difference of two monomials by their sum, like (x + 3)(x − 3) or (5x − 2)(5x + 2), the inner and outer products turn out to be opposites. Adding opposites gives you 0, so the middle term you would usually get disappears.
(x + 3)(x − 3) = x2 − 3x + 3x − 32 = x2 − 9
(5x − 2) (5x + 2) = (5x)2 + 2·5x − 2·5x − 22 = 25x2 − 4
Multiplying a sum of two monomials by their difference gives you the difference of the square of the first term and the square of the last term.
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
(a + b)(a − b) = a2 − b2
ALGEBRA TRAP
Don’t forget to square the coefficient of the variable term when you square a binomial. (3x + 5)2 = (3x + 5)(3x + 5), and when you FOIL, 3x·3x is 9x2, not 3x2.
CHECK POINT
Use special product shortcuts to complete each multiplication.
21. (t − 4)2
22. (y − 7)(y + 7)
23. (2x − 1)2
24. 
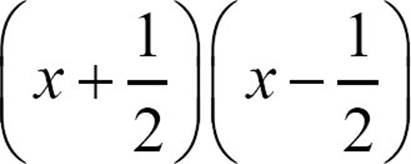
25. (2t − 5)(2t + 5)
26. (3x + 5)2
27. (5a − 3)2
28. (x2 − 5)2
29. (x2 + 1)(x2 − 1)
30. (5t2 − 2t)(5t2 + 2t)
You already know some strategies for polynomial multiplication. The distributive property is your method for a monomial multiplied by a larger polynomial, and the FOIL rule applies to the specific but common situation of a binomial multiplied by a binomial. Now we need to have a look at how to deal with larger problems.
Larger Products
The general rule for multiplying two polynomials, of any size, is that you multiply each term of the first polynomial by each term of the second polynomial. For small problems, that’s not too difficult to keep track of, but when the problems are larger, we need a way of keeping things organized.
Being asked to multiply (2x2 + 7x − 3)(x3 − 4x2 + 8x + 3) can be challenging if you look at it all at once. The trick is to break it into lots of little multiplications and then put the like terms together at the end. You could just multiply 2x2 times each term of the second polynomial, then multiply 7x times each term, and then multiply −3 times each, but it’s easy to lose your place or miss a term. So a vertical arrangement will make it easier to stay organized. Place the polynomials one under the other, usually with the longer one on top.
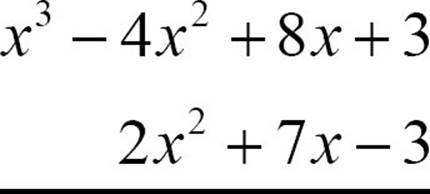
Start with the rightmost term of the bottom polynomial, the −3, and multiply each term of the upper polynomial by −3.
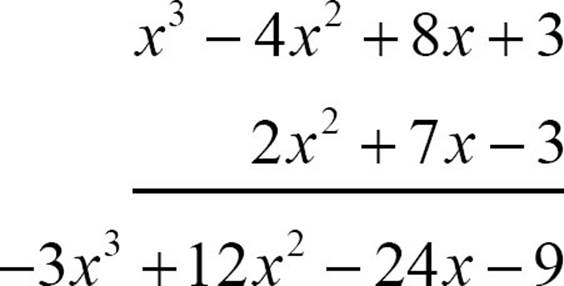
Place a 0 under the rightmost term of that partial product. Then multiply each term of the upper polynomial by the 7x.
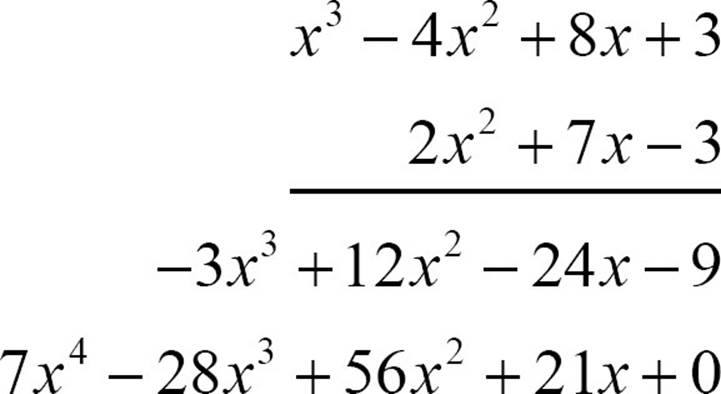
DEFINITION
A partial product is the polynomial produced by multiplying by just one digit or term in a multiplication of polynomials or in the multiplication of multi-digit numbers.
For the third line, start with two zero terms, then multiply each term of the upper polynomial by 2x2.
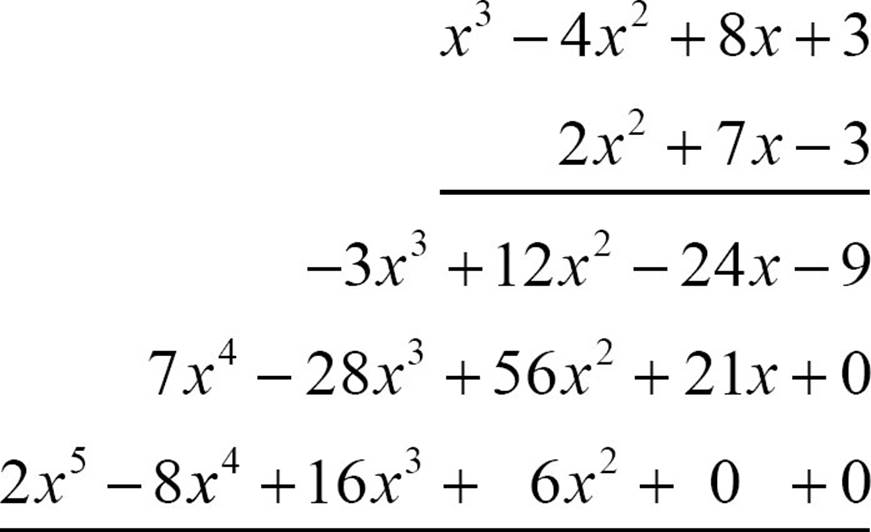
Once you’ve multiplied by each term of the bottom polynomial, the last step is to combine like terms, and they should be nicely lined up in columns.
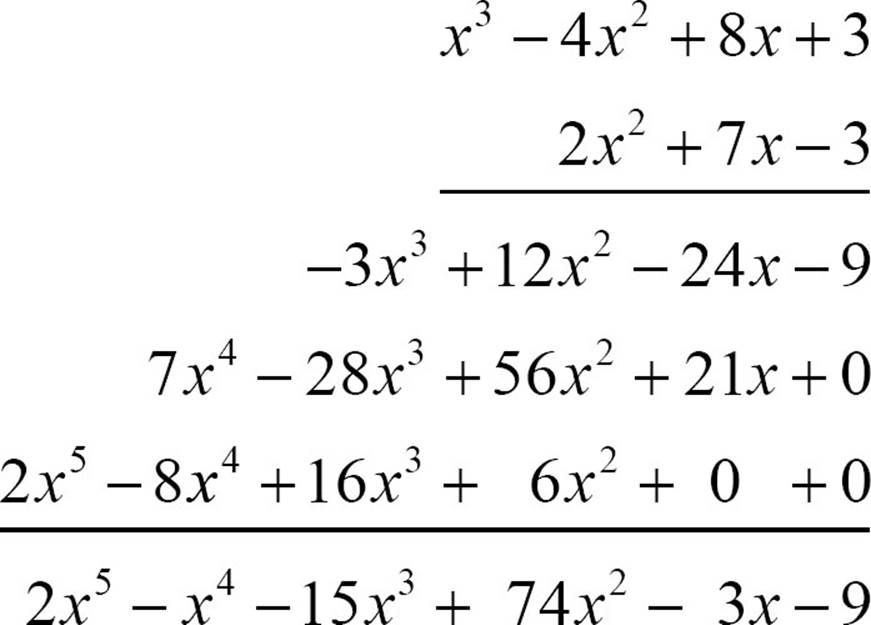
If one or both polynomials have missing powers of the variable, you can insert zero terms to hold a place and help keep like terms aligned. The product (t2 − 3t + 2)(t5 − 7t3 + 5) can be rewritten as (t2 − 3t + 2)(t5 + 0t4 − 7t3 + 0t2 + 0t + 5). When you set up the vertical format, it looks like this.
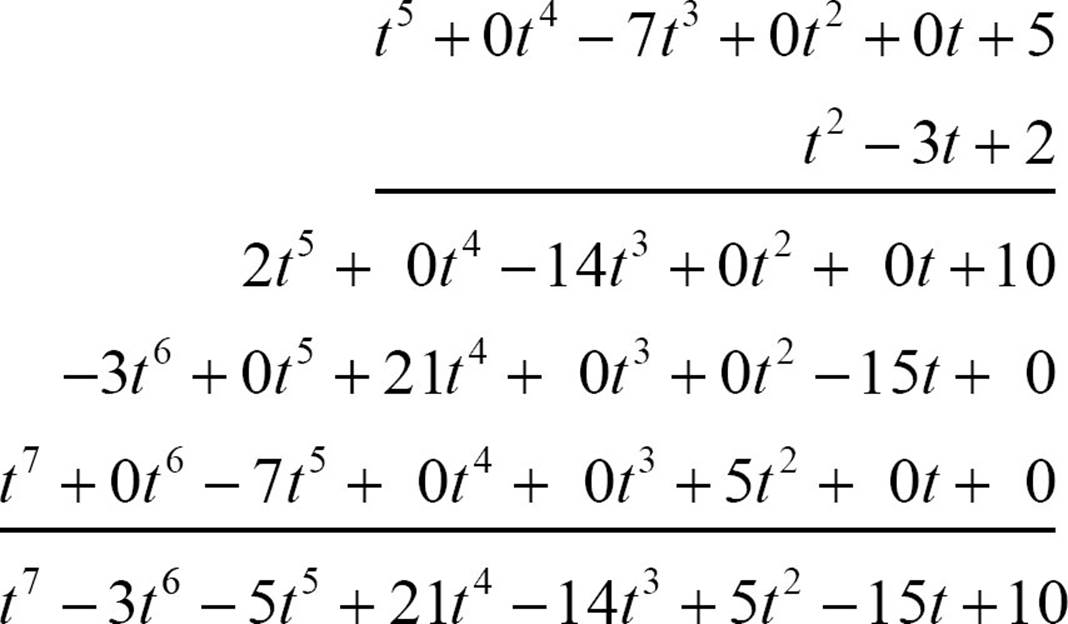
CHECK POINT
Complete each multiplication. Use the format that feels most comfortable.
31. (4x − 3)(3x2 + x − 6)
32. (x + 5)(x2 + 2x + 3)
33. (2y − 3)(y2 − 3y + 2)
34. (2a − 5)(a3 − 5a2 + a − 3)
35. (3x − 2)(x2 − 3x − 6)
36. (2y − 3) (4y3 − y2 + 2y + 5)
37. (x − 2)(x3 + 5x − 7)
38. (3a + 1)(a2 − a)
39. (2x3 − 1)(6x4 + 3x2 + 1)
40. (t − 4)(t2 + 4t + 16)
Dividing Polynomials
Once you know how to multiply polynomials, it’s natural to think about the inverse, or opposite operation. You won’t often need to divide polynomials, but there are two techniques you can use for this operation.
Single Term Divisor
Just as the basis of all polynomial multiplication is the multiplication of one monomial by another monomial, the root of all division of polynomials is division by a single term. Dividing a monomial by a monomial means that you divide the coefficients, and then deal with dividing the variables by again following the rules for dividing powers of the same base.
To divide −8x3 by 4x, think of the quotient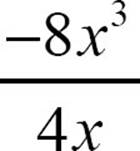 
as 
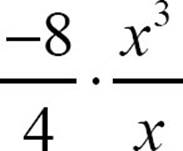. The numerical coefficient will be −2, and 
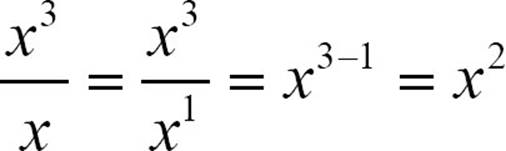, so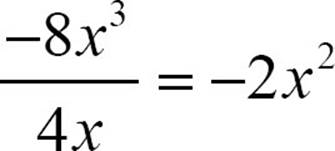 
.
TIP
If you’re dividing a polynomial by a monomial and you encounter one or more terms for which the coefficients don’t divide evenly, you’ll find it more convenient to leave the quotients as improper fractions rather than decimals or mixed numbers. Simplify the fractions but don’t fuss with decimals that might not terminate.
To divide a larger polynomial by a monomial, for example,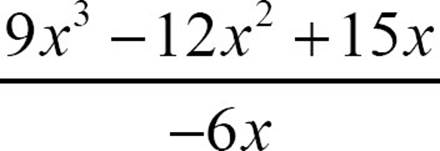 
, you’ll break the quotient into a sum of divisions.
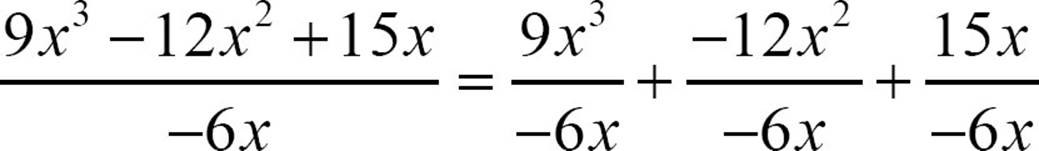
Then do each division of monomial by monomial.
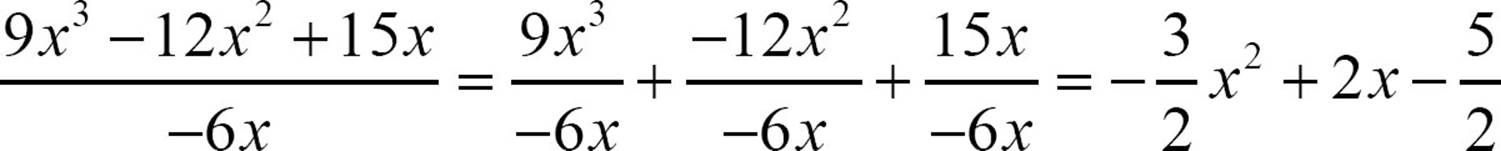
Not every division problem involving polynomials will produce a polynomial. Remember that the monomials that make up a polynomial must involve positive integer powers of the variable. The exponents can’t be negative in a polynomial, but dividing powers could certainly produce negative exponents.
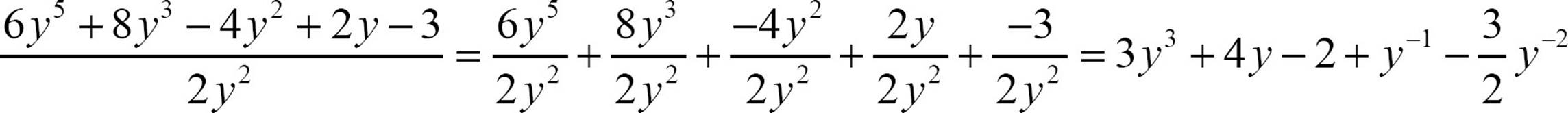
You can give that quotient using negative exponents, with the understanding that the quotient is not a polynomial. You can use the language of your early experience with division and talk about a remainder. The first three terms of the quotient form a polynomial. You could take the division that far, and say that 6y5 + 8y3 − 4y2 + 2y − 3 divided by 2y2 is 3y3 + 4y − 2 with a remainder of 2y − 3. Or you could write the remainder over the divisor as a fraction and say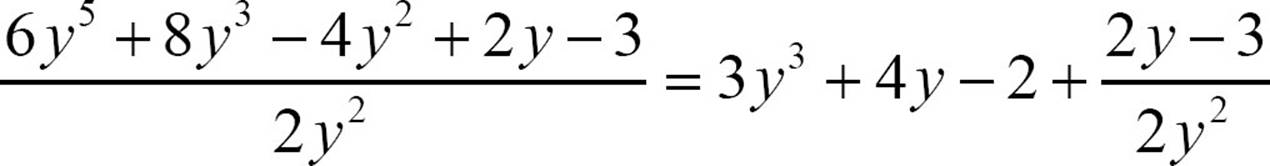 
.
CHECK POINT
Perform each division, putting your answer in simplest form.
41. (8x + 24) ÷ 8
42. (28x2 + 84x) ÷ 7x
43. (6x5 − 12x4 + 9x3) ÷ 3x
44. (15y3 − 20y2 − 10y) ÷ −5y
45. (8x4 − 12x3) ÷ (4x2)
46. (15t6 − 21t3) ÷ (− 3t2)
47. (16y5 − 24y3) ÷ (−8y3)
48. (14x6 − 42x4 + 56x2) ÷ (−14x2)
49. (−9a4 + 27a3 − 81a2) ÷ (−9a2)
50. (24x7 − 16x5 − 48x4 + 36x3) ÷ (−4x2)
Long Division
When the divisor is a polynomial with more than one term, you can’t use the term-by-term division strategy that you used with a monomial divisor. Instead, you have to fall back on the algorithm for long division that we learned in arithmetic.
DEFINITION
An algorithm is a step-by-step procedure for performing a task.
To divide 12x3 + 8x2 − 10x + 14 by x + 2, set up a long division problem with 12x3 + 8x2 − 10x + 14 as the dividend and x + 2 as the divisor.
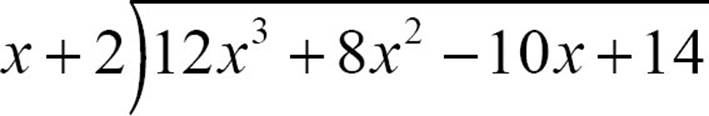
In arithmetic, you often used estimates to get you through long division. In polynomial long division, you can estimate using the first term of the divisor. In this case, that’s x. Start by asking what 12x3 ÷ x will give you. The answer to that is 12x2, so put 12x2 up in the quotient.
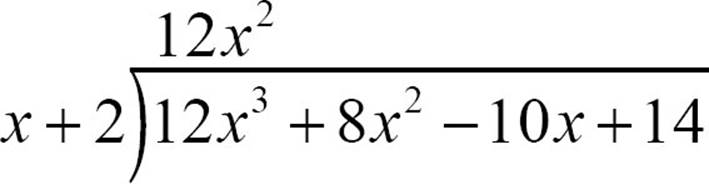
Of course, 12x2 isn’t the whole quotient. It’s just the first term. Multiply 12x2 (x + 2), to get 12x3 + 24x2, and put that underneath the first two terms of the dividend.
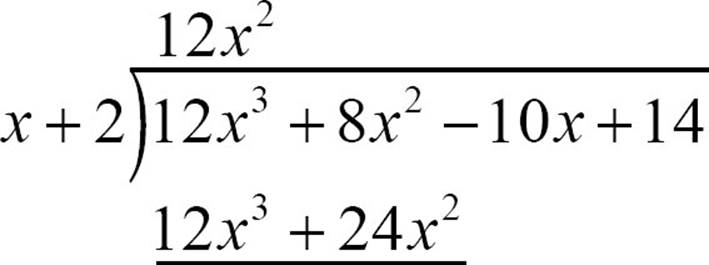
Subtract 12x3 + 24x2 from the terms above, remembering that both terms are subtracted, not just the first one.
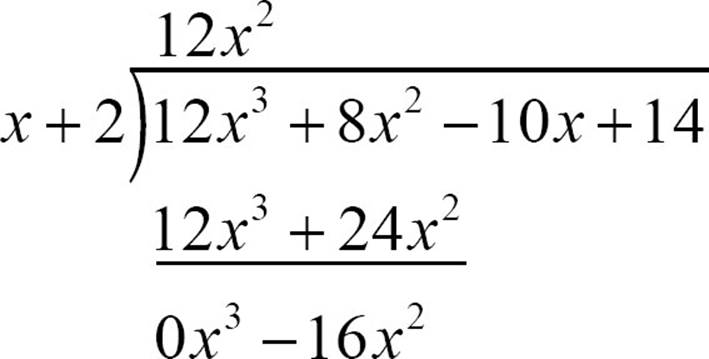
The 0x3 can be dropped (the first term of your difference will always go away). Now, bring down the last two terms of the dividend.
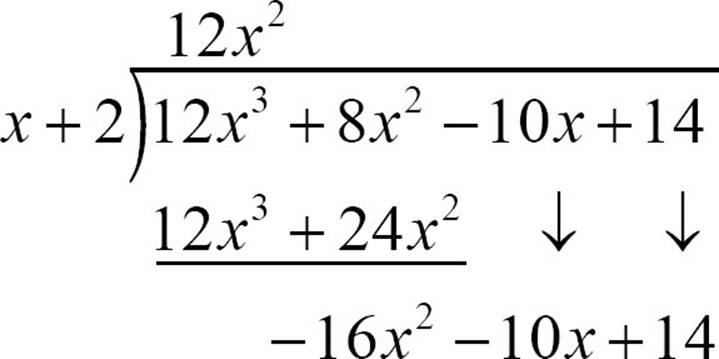
At this point, you have to decide if you’re done. Will continuing produce negative exponents in the quotient? The quick way to decide is to compare −16x2 − 10x + 14 to the divisor x + 2. Because the degree of −16x2 − 10x + 14 is higher than the degree of x + 2, you can continue.
Continuing the division process means dividing −16x2 − 10x + 14 by x + 2. Follow the same steps. Estimate by dividing −16x2 by x, then multiply that estimate times x + 2, place that product underneath, subtract, and bring down any terms from the dividend not yet used. Here’s how it looks.
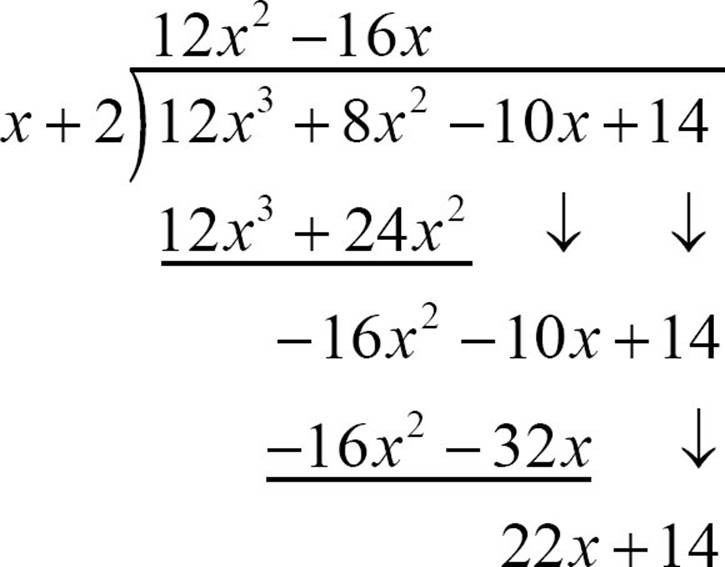
Compare 22x + 14 to x + 2. If the degree of the remainder polynomial is lower than the degree of the divisor, it’s time to stop, but you’re not there yet. 22x + 14 and x + 2 have the same degree, so you can go one more round.
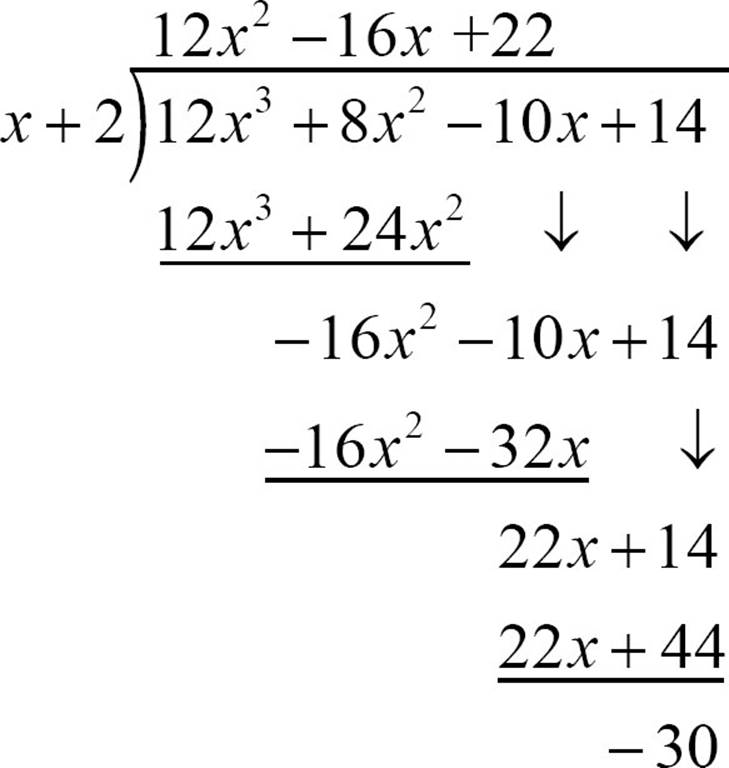
Once the remainder is an expression with a lower degree than the divisor, you can stop dividing. You can say that 12x3 + 8x2 − 10x + 14 divided by x + 2 is 12x2 − 16x + 22 with a remainder of −30, or you can put that remainder over the divisor as a fraction and say the quotient is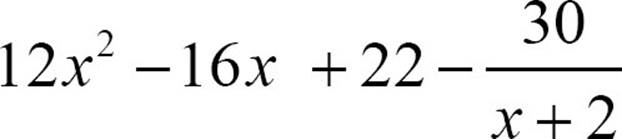 
. You can check your work by multiplying the quotient times the divisor, then adding on the remainder. If the result is the original dividend, our work is correct.
(x + 2) (12x2 − 16x + 22) − 30 = (12x3 − 16x2 + 22x + 24x2 − 32x + 44) − 30
= (12x3 + 8x2 − 10x + 44)– 30
= 12x3 + 8x2 − 10x + 14
If either the dividend or the divisor is missing powers of the variable, you’ll probably find it easier to manage the division if you insert terms with zero coefficients to fill the spaces of the missing terms. If you need to divide x3 − 8 by x − 2, set it up as (x3 + 0x2 + 0x − 8) ÷ (x − 2).
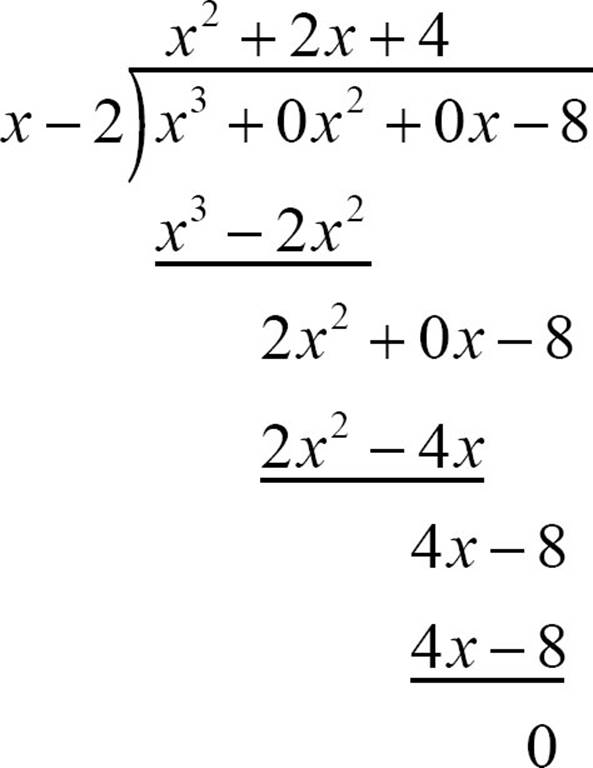
CHECK POINT
Complete each long division and express the result as quotient plus remainder over divisor.
51. (x2 + 11x + 30) ÷ (x + 5)
52. (x2 + 10x + 24) ÷ (x + 4)
53. (z2 − 15z + 56) ÷ (z − 8)
54. (b2 − 3b − 28) ÷ (b + 4)
55. (6x2 + 13x + 6) ÷ (3x + 2)
56. (7y2 − 3y − 4) ÷ (y − 1)
57. (9x2 − 42x + 45) ÷ (3x − 8)
58. (2b2 − 7b + 3) ÷ (b − 3)
59. (x4 − 2x2 + 1) ÷ (x2 − 2x + 1)
60. (3x4 − 17x2 + 10) ÷ (x2 − 5x)
The Least You Need to Know
· To multiply a monomial times a polynomial, use the distributive property.
· To multiply two binomials, use the FOIL rule.
· For larger polynomials, arrange them vertically and multiply each term of the bottom polynomial by each term of the top one, and then combine like terms.
· To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
· To divide by a larger polynomial, use the long division algorithm.