Idiot's Guides: Algebra I (2015)
Part V. Radical, Quadratic, and Rational Functions
Chapter 15. Quadratic Equations
In This Chapter
· Solving quadratic equations by taking square roots
· Using the quadratic formula to solve any quadratic equation
· Determining the number of solutions by looking at the discriminant
· Applying the Zero Product Property to solve a quadratic equation by factoring
You may have noticed as you worked your way through the preceding chapters that while we talked about rules for exponents, and expressions involving exponents, we haven’t solved equations that involved exponents. Well, the time has come.
In this chapter, we’ll look at methods for solving equations that involve a second power of the variable. Later in your exploration of algebra, you’ll investigate other powers of the variable, but for now, we’ll focus on equations involving variables squared. We’ll call on many of the skills you’ve already learned, putting them together in new ways to solve equations from this new category.
Quadratic Equations
A quadratic equation is defined as an equation that is in the form (or can be put in the form) ax2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. That means it’s an equation that contains a term in which the variable is squared. There may be another variable term with the variable to the first power. There may be a constant term. Those terms may or may not be there, but what makes it a quadratic equation is the squared term.
DEFINITION
A quadratic equation is an equation that includes a term in which the variable is squared. There may also be a variable term in which the variable appears but is not squared, and a constant term.
Examples of quadratic equations include equations as simple as x2 = 4, which fits the pattern if you think of it as 1x2 + 0x – 4 = 0. The equation x(x + 8) = 0 is also an example of a quadratic equation, because although you don’t see a square right away, when you distribute to remove the parentheses, it becomes x2 + 8x = 0, a quadratic with a constant term of 0. Of course, many quadratics will look just like the model in the definition, like 3x2 + 5x + 9 = 0.
A key characteristic of quadratic equations is that quadratics have two solutions. If x2 = 4, x might be 2 or x might be -2. Rules for signs state that both 22 and (−22) equal 4. The two solutions of a quadratic equation won’t always be a number and its opposite, but you can expect to see two solutions in most quadratics.
The Square Root Method
When you’re faced with a simple quadratic equation, like x2 = 4, you may be able to use a little logic and your knowledge of exponents to figure out the solutions. Asking yourself, “what number, times itself, gives me 4?” may be enough. You might need a little prodding to remember the negative possibility, but if you know to expect two solutions, that should work out.
What happens if you change that equation to x2 = 5? You probably can’t pull the numbers out of your head, because no integer, squared, gives you 5, but you know you want to ask that question: what number, squared, equals 5? The mathematical way to ask that question is, “what is the square root of 5?” If x2 = 5,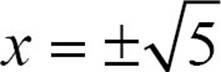 
. The square root of 5 is an irrational number, so you want to leave that answer in simplest radical form for an exact answer, or use a calculator (or table of square roots) to get an approximate answer.
This is the heart of the square root method. You isolate the squared variable, then take the square root of both sides, and put the answer in simplest radical form. Here’s another example.
x2 −43 = 5
Isolate the x2.
x2 = 48
Take the square root of both sides. Don’t forget, you want both the positive and the negative square root.
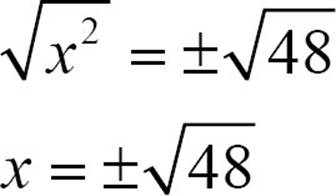
Put the radical in simplest form.
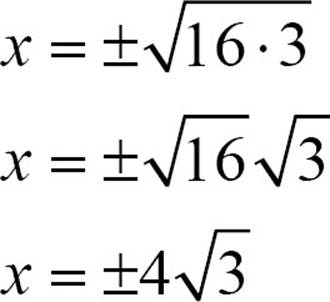
That’s a nice method for solving equations that can be written as x2 = a, but if that were all it could do, it wouldn’t be much help. The square root method is not the most powerful method and it won’t solve every quadratic equation, but it can deal with some more complicated equations. It can be used to solve any equation that is in the form (some expression)2 = a constant.
If you need to solve the equation (x + 3)2 = 81, you can use the square root method with a little bit of extra work. Take the square root of both sides.
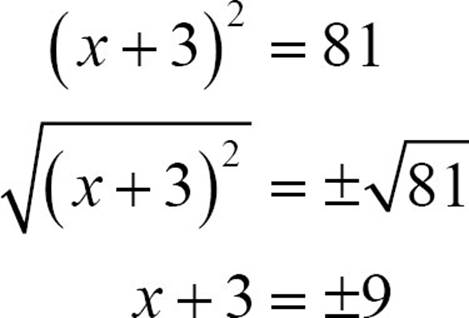
Just as taking the square root of x2 will undo the squaring and get us back to x, taking the square root of (x + 3)2 will undo the squaring of the quantity. This leaves you not with x = a number, but with x + 3 equal to 9 or to -9. The extra step will be translating that information into two little equations, each of which will give you one solution. It looks like this.
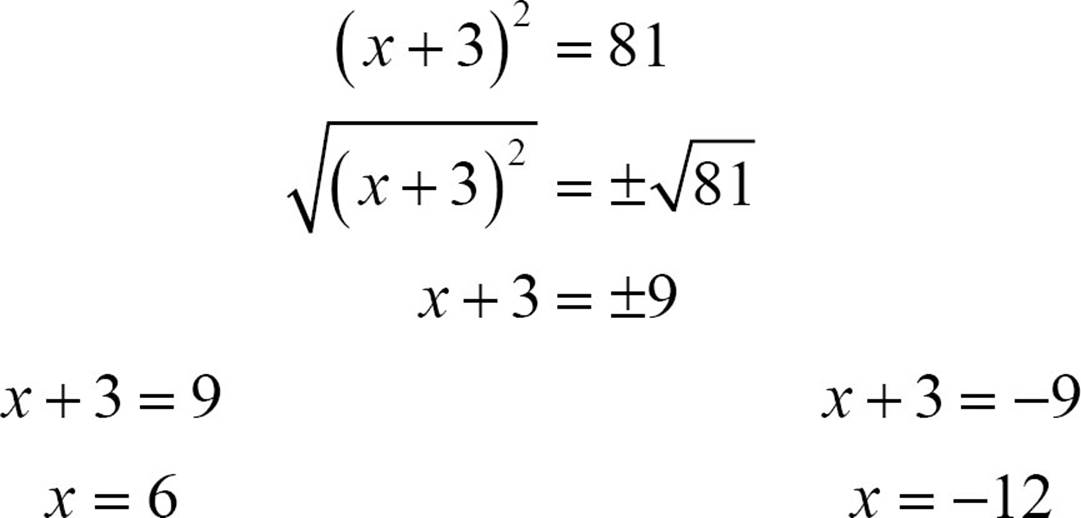
The solutions of (x + 3)2 = 81 are x = 6 or x = −12. You can check that by substituting each solution, one at a time, into the original equation.
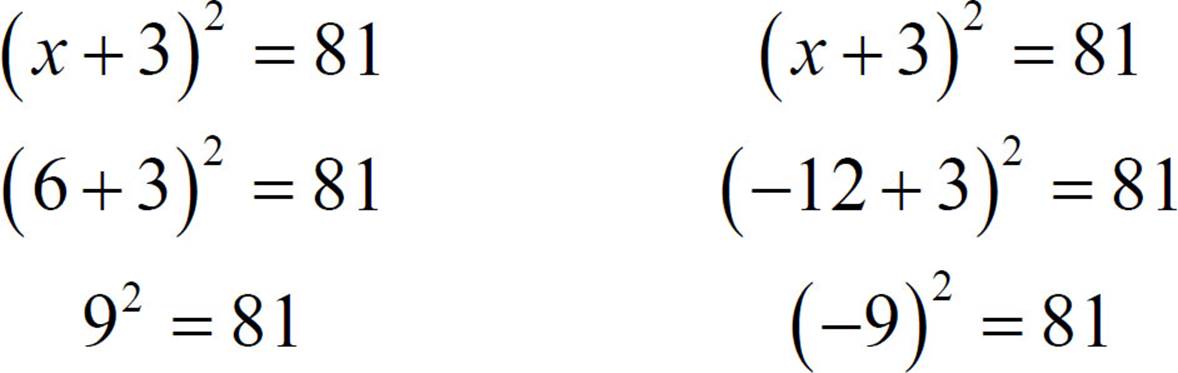
TIP
If the (expression)2 equals a negative number, you can’t take the square root of both sides because negative numbers don’t have square roots, at least, not in the real numbers. If you find that (expression)2 = a, the equation has no real solution.
Here’s another example of an equation that can be solved by the square root method: 4x2 + 20x + 25 = 16. You can use the square root method on any equation in the form (some expression)2 = a constant, and 4x2 + 20x + 25 = 16 certainly doesn’t look like that. If you remember the special forms you learned when we talked about multiplying polynomials and about factoring, you might recognize 4x2 + 20x + 25 as a perfect square trinomial. You can rewrite 4x2 + 20x + 25 = 16 as (2x + 5)2 = 16 as (2x + 5)2 = 16 and that will let you use the square root method.
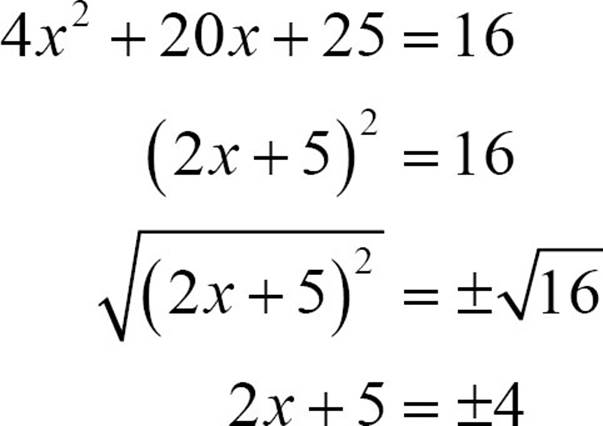
Now break that up into two equations.
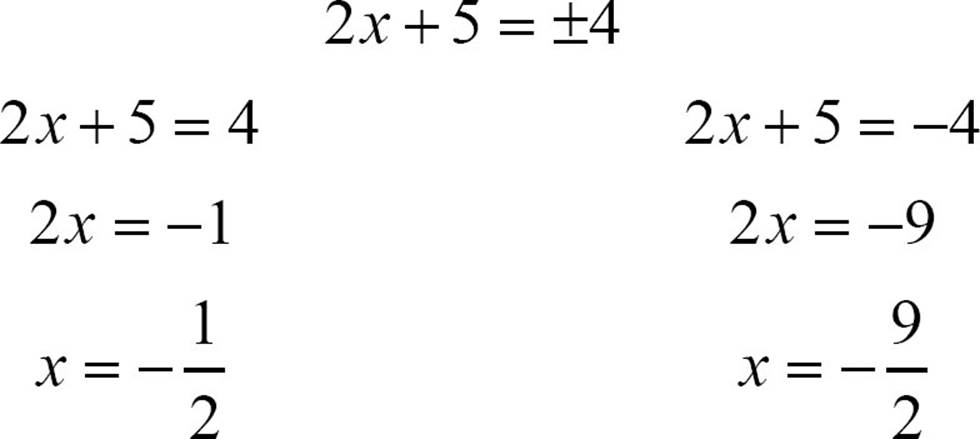
ALGEBRA TRAP
Because your first exposure to quadratic equations is usually equations of the form x2 = a constant, where the solutions are the positive and negative of the same number, it’s easy to think that all quadratics have solutions that are the positive and negative of the same number. That’s not the case. You should expect two solutions, but don’t solve for one and assume the other is its opposite. Take your time and find both solutions.
The two solutions of 4x2 + 20x + 25 = 16 are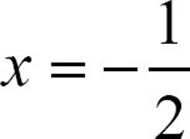 
and 
.
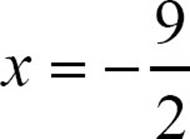CHECK POINT
Solve each equation by the square root method.
1. x2 = 81
2. 2x2 = 50
3. x2 − 10 = 6
4. (x − 7)2 = 4
5. (x + 3)2 − 1 = 8
6. x2 − 6x + 9 = 1
7. x2 + 121 = 22x
8. (3x − 4)2 = 49
9. 4x2 + 4x + 1 = 36
10. (5x − 8)2 = 18
The Quadratic Formula
Many years ago, people realized that although there were other methods for solving quadratic equations, they were a lot of work, and often very messy arithmetic.
Luckily for us, some patient soul got an idea. What would happen if you took the general pattern of a quadratic equation, ax2 + bx + c = 0, right from the definition, and went through all the steps of the other method, with the a, b, and c still in there? We won’t go through all the steps, because, as you can imagine, it is messy. But that patient soul did go through all the steps, and here’s how it turned out.
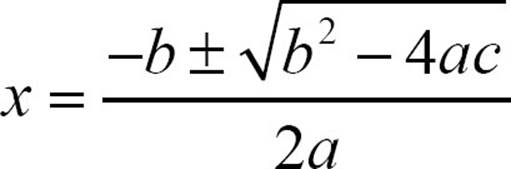
That equation, the solution that patient person arrived at has come to be known as the quadratic formula. That formula is our good fortune. It’s an easy way to solve a quadratic equation, without worrying about whether it’s a perfect square, or whether it can be made a perfect square. We just need to match our equation up with ax2 + bx + c = 0, identify a, b, and c, and plug those values into the quadratic formula.
DEFINITION
The quadratic formula is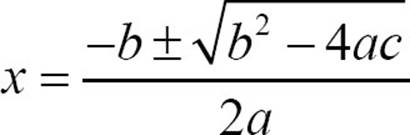 
. It can be used to find solutions for any quadratic equation of the form ax2 + bx + c = 0 by substituting the values of a, b, and c and simplifying.
To solve the equation x2 − 3x + 7 = 5, begin by gathering all the terms on the left side, equal to 0. Do that by subtracting 5 from both sides.
x2 − 3x + 7 = 5
x2 − 3x + 2 = 0
Compare x2 − 3x + 2 = 0 to ax2 + bx + c = 0 to identify a, b, and c.
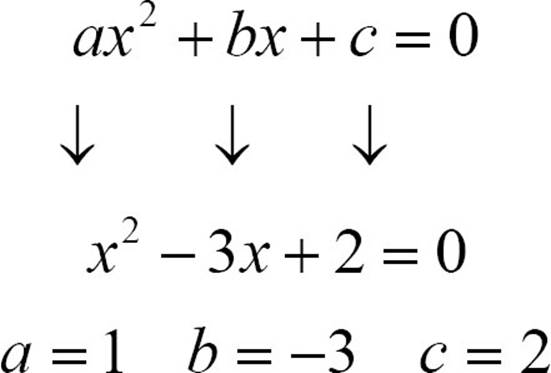
Now plug the values into the quadratic formula and replace the a with 1, the b with -3, and the c with 2.
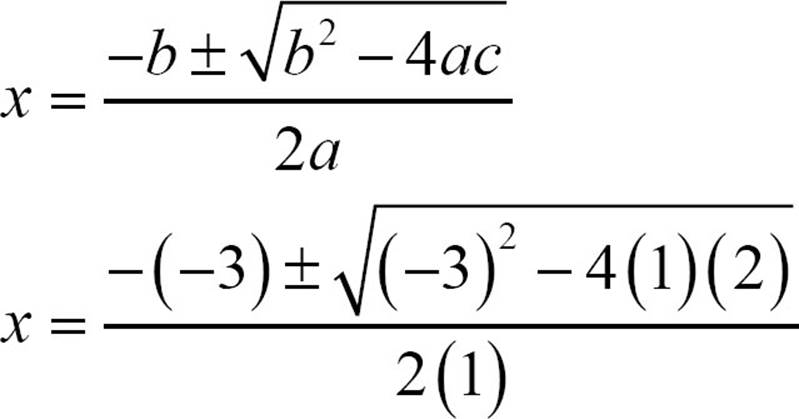
Simplify as much as possible.
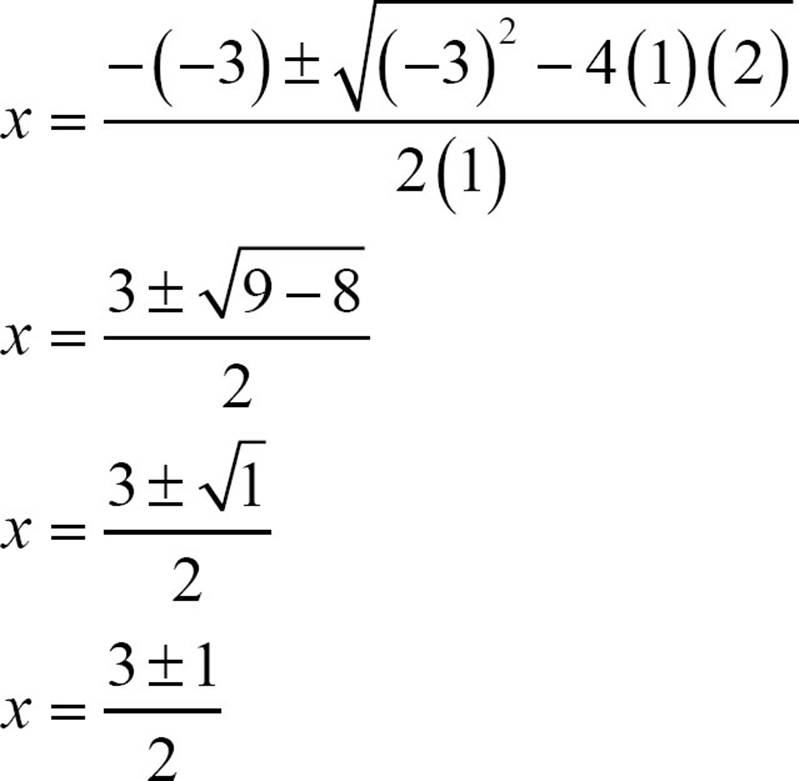
Break into two equations.
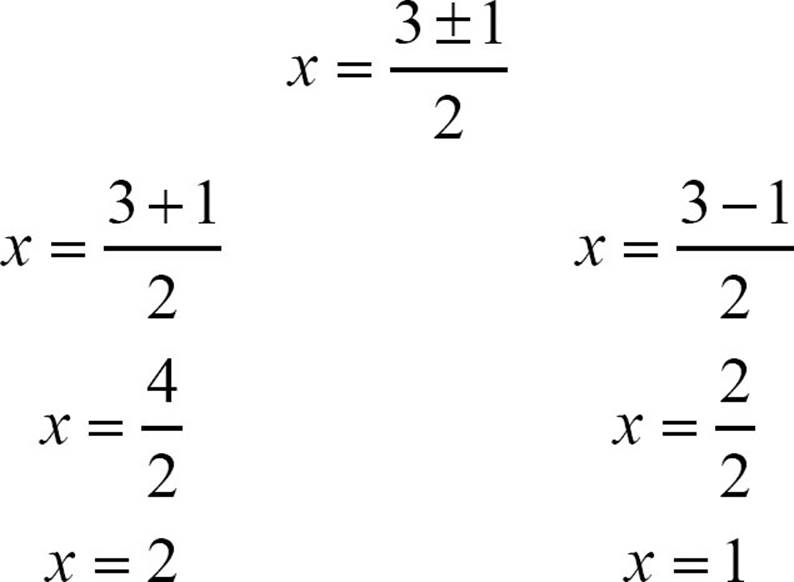
While that may not seem all that much simpler, the quadratic formula does have the advantage of solving any quadratic, and it’s really just plug in and simplify.
TIP
If your quadratic equation does not have an x-term, a first power term, then b = 0 in the quadratic formula. If there is no constant term, just an x2 term and an x-term, then c = 0.
Here’s another example. Solve 2x2 − 5x − 2 = 0.
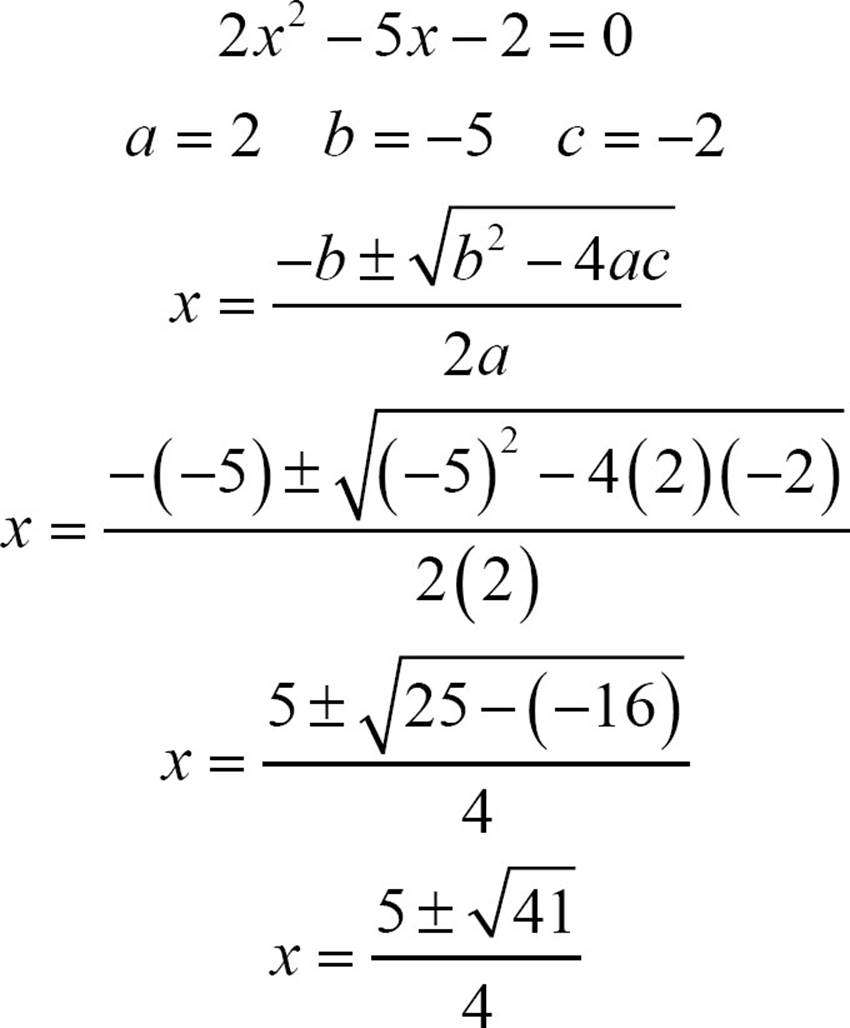
When the solutions are irrational, as they are here, you just need to be sure the radical is in simplest form, and you’re done. The two solutions are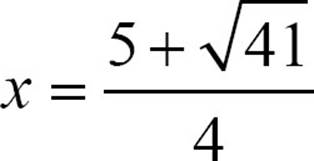 
and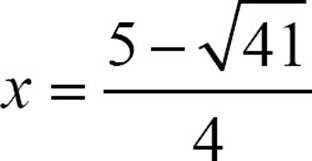 
.
CHECK POINT
Solve each quadratic equation by using the quadratic formula.
11. x2 + 4x − 21 = 0
12. t2 = 10 − 3t
13. y2 − 4y = 32
14. x2 = 6 + x
15. 9 = 6w + w2
16. x2 + 7x + 15 = x
17. 4 x2 − 2 = x + 1
18. 3x2 − 1 = 2x
19. x2 + 6x = 4
20. x2 + 4x − 2 = 0
Using the Discriminant
The portion of the quadratic formula under the radical, b2 − 4ac, is called the discriminant. The name comes from the definition of discriminate: recognize a distinction. The discriminant allows us to distinguish between quadratic equations that have, as expected, two distinct real solutions, quadratic equations that have no solution, and quadratic equations that appear to have only one solution.
I say “appear to” because they actually have two solutions that are the same. This is sometimes called a double root. The equation x2 = 0 is a simple example of an equation with a double root. Technically, it has two solutions: x = 0 and x = 0. That really only looks like one solution.
DEFINITION
The discriminant is the portion of the quadratic formula that appears under the radical, b2 − 4ac. It can be used to tell how many solutions (and what type of solutions) a quadratic equation will produce.
A double root, or double solution, is a solution that occurs twice for the same equation, because the equation was a perfect square trinomial.
If the discriminant is a positive number, the equation will have two distinct real solutions. If the discriminant is positive and a perfect square, those solutions will be rational numbers. If it’s positive but not a perfect square, the solutions will be irrational.
If the discriminant is zero, the equation will have a double root, and therefore appear to have only one solution.
If the discriminant is a negative number, it will be impossible to take its square root, so the equation will have no solution.
CHECK POINT
Find the discriminant.
21. x2 − 8x + 12 = 0
22. x2 − 3x − 9 = 0
23. 2x2 + 5x + 4 = 0
24. x2 + 8x + 16 = 0
25. x2 − 9 = 0
Use the discriminant to determine the number of solutions, but do not solve.
26. x2 − 5x + 4 = 0
27. 2x2 − 5x − 4 = 0
28. 9x2 + 4 = 0
29. x2 − 8x + 16 = 0
30. 3x2 − 2x − 1 = 0
In the previous sections of this chapter, we looked at various methods for solving quadratic equations. The square root method is quick and easy in the right situations, and the quadratic formula can be counted on to solve any quadratic equation. Even the quadratic formula can lead to some messy arithmetic at times, however, and that’s why many people find our last method, solving by factoring, to be their favorite.
Like the other methods, factoring is not perfect. Not every quadratic expression can be factored, as you’ve seen. Some equations that can be solved by the quadratic formula just won’t yield to factoring, but when factoring does work, it’s often the fastest, simplest method.
The Factoring Method
The factoring method is based on something called the zero product principle. That’s a very formal name for something you likely already know. Think of two numbers that, when multiplied, produce a product of 0. Got them? Zero and what else? Any time two numbers multiply to 0, at least one of them must have been 0. That’s the zero product principle. If ab = 0, then either a = 0 or b = 0 or both.
We’re going to pull together that principle and what we know about factoring to solve many quadratic equations. Suppose you want to solve x2 + 11x + 28 = 0. You could use the quadratic formula, but the numbers are going to get large. So let’s try this. If you can write x2 + 11x + 28 as a product and factor it, you’ll have a product that equals zero, and that means one or both of the factors are 0.
There is a 0 on the right side of the equation. That’s important. Factoring won’t do any good if you don’t have that. Let’s factor.
x2 + 11x + 28 = 0
(x + 4)(x + 7) = 0
According to the zero product property, if (x + 4) and (x + 7) multiply to 0, then either x + 4 = 0 or x +7 = 0 or both. Let’s look at those two possibilities.
The two solutions of x2 + 11x + 28 = 0 are x = − 4 or x = − 7.
When the quadratic expression is factorable, this is often the quickest way to solve the equation. Any type of factoring—greatest common factor, FOIL factoring, special forms—can be used, but the quadratic expression must be equal to zero before you begin to factor. Here’s another example.
Solve 5x2 = 40x. Start by getting all the non-zero terms on the left side, equal to 0.
5x2 = 40 x
5x2 − 40x = 0
Now we can factor out a common factor of 5x from both terms.
5x2 − 40x = 0
5x (x − 8) = 0
Use the zero product principle to make two equations by setting each factor equal to 0.
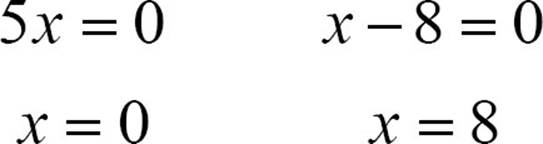
The solutions of 5x2 = 40x are x = 0 or x = 8.
Let’s take a look at an example that doesn’t look like a quadratic at first. Solve the radical equation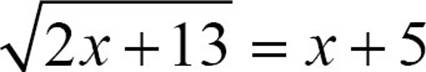 
. Remember that our strategy for solving radical equations is to isolate the radical and square both sides. The radical is isolated, but squaring x + 5 is going to result in a squared term and leave us with a quadratic equation.
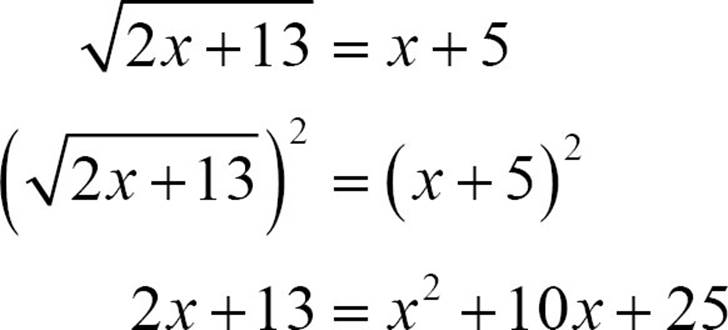
Gather all the non-zero terms on one side, equal to 0, and factor.
0 = x2 + 8x + 12
0 = (x + 2)(x + 6)
Set each factor equal to 0 and solve.
Don’t forget that when you solve radical equations, even radical equations that turn into quadratic equations, you must check your solutions. Extraneous solutions are always possible.
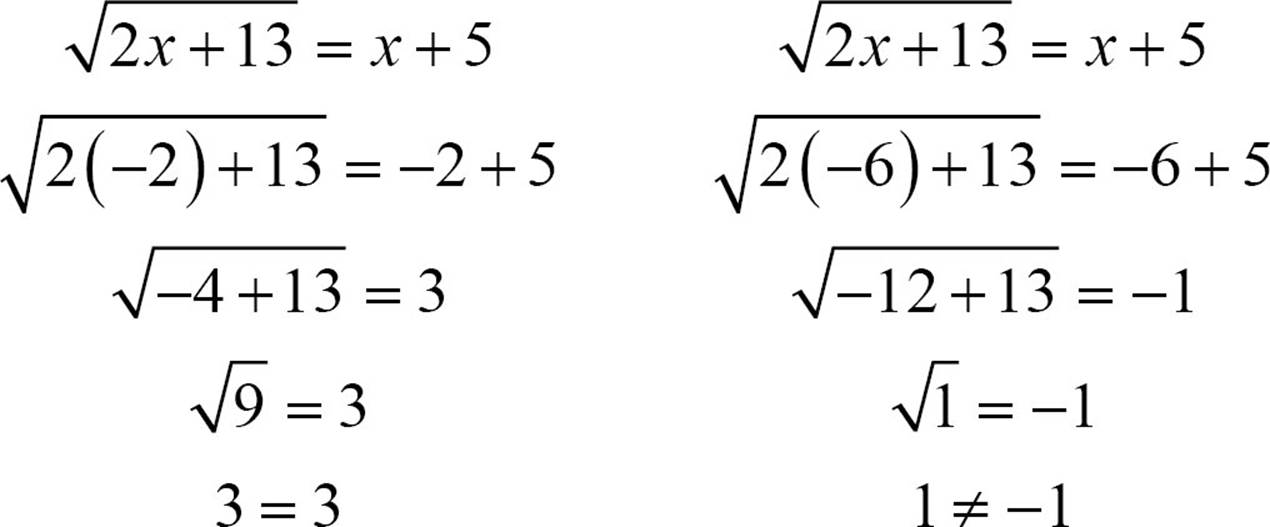
One of the solutions checks, but the other does not. Reject the extraneous solution (x = − 6) and the solution is x = −2. The quadratic equation that was created when you squared both sides does have two solutions, but only one of them is a solution of the original radical equation.
CHECK POINT
Solve each quadratic equation by factoring, if possible. If the expression is not factorable, use the quadratic formula.
31. x2 + 5x + 6 = 0
32. x2 + 12 = 7x
33. x2 − 3x − 4 = 0
34. x2 − 6x + 5 = 0
35. x + 2 = 3x2
36. 6x2 − 5x − 6 = 0
37. x2 + 3x = 8 + x
38. x2 + x − 20 = 0
39. x2 + 3x = 0
40. 3x2 − 3x + 1 = x2
The Least You Need to Know
· Quadratic equations in the form (some expression)2 = a constant, and those that can be conveniently put in that form, can be solved by taking the square root of both sides.
· Any quadratic equation ax2 + bx + c = 0 can be solved by the quadratic formula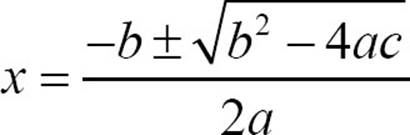 
.
· The part of the quadratic equation known as the discriminant b2 − 4ac tells how many solutions to expect. If it’s positive, there will be two solutions. If it’s zero, there will be one solution, and if the discriminant is negative, the equation has no real solution.
· If a quadratic expression is factorable and equal to zero, the equation can be solved by factoring and setting each factor equal to zero.