Idiot's Guides: Algebra I (2015)

Part I. Introduction to Algebra

All my favorite detective stories begin by setting the scene, letting us know where we are, and at least a little bit of how we got there. Once the crime has been committed or the mystery has been introduced, the principal characters begin to gather the essential information: who, what, where, when, how, and why. Of course, that’s never enough, or it would be a very short story, but it is a good way to start our investigation of algebra.

In these first three chapters, we’ll look at a little bit of background of arithmetic that gives rise to algebra, and build some basic understandings and skills that are the foundation for a study of algebra. We’ll transfer the ideas of arithmetic to a world that includes variables, and explore the essential concept of a function, the relationship at the heart of much algebraic work.

Chapter 1. Arithmetic to Algebra

In This Chapter

·  Understanding the workings of our number system

·  Reviewing the rules for signed numbers

·  Practicing shortcuts for exponents

·  Applying the order of operations

Before a doctor can learn to diagnose an illness, she must understand the workings of the human body. Before a forensic scientist can analyze evidence, he must have a thorough background in the sciences. Anyone who wants to tackle the challenges of algebra needs first to understand the system of arithmetic from which algebra grows. So let’s begin with arithmetic, and then move on to algebra. In this chapter, we’ll look at some key elements of how arithmetic works: numbers, operations, rules, and shortcuts. That will be a good review and also give us a chance to talk about why it works the way it does.

The Real Numbers

The set of numbers you use for most of your work is a set called the real numbers. This set is made up of several other sets of numbers.

DEFINITION

The rational numbers are all numbers, positive or negative, that can be written as a fraction. Any number that doesn’t fit that description is irrational. The real numbers are all numbers; positive and negative, rational and irrational.

The Real Numbers

Early in your experience with arithmetic, you work with just whole numbers. Gradually, your mathematical world expands to include fractions and decimals, and negative as well as positive numbers. At that point, you’re using the rational numbers.

The whole numbers, made up of zero and the counting numbers, form the set {0, 1, 2, 3, 4 …}. Include the opposites of those counting numbers, and you have the integers: {…-4, -3, -2, -1, 0, 1, 2, 3, 4…}. The rational numbers are made up of all numbers that can be written as a ratio, or fraction, of two integers, so they include all the positive and negative fractions, and all the positive and negative decimals that are equivalent to fractions.

TIP

The … in a set of numbers means that the list continues forever. If there’s a pattern to what you can see of the list, the pattern continues.

Eventually, however, you realize that there are decimals that aren’t equivalent to fractions. When you change a fraction to a decimal by dividing the numerator by the denominator, one of two things happens: either the decimal terminates, as 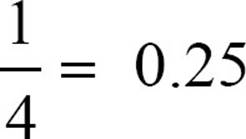terminates, or the decimal goes on forever, repeating a pattern, as 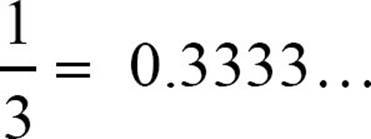repeats. When you realize that there are decimals that go on forever but don’t repeat, like 0.112123123412345…, you realize there are irrational numbers. The rational numbers and the irrational numbers together make the real numbers.

The real numbers are basically all the numbers you use, all the numbers you can think of, but surprisingly, not all the numbers you can imagine. There are other numbers mathematicians think about that don’t fit our image of real numbers, and they are called the imaginary numbers. We’ll take a little peek at them later on. For now, we’re working with the real numbers.

DEFINITION

Imaginary numbers are numbers that don’t fit in the real number system, but that mathematicians use to solve certain types of problems.

Basic Operations

Most people would say that there are four basic operations of arithmetic: addition, subtraction, multiplication, and division. They’d be right, but other people would say there are only two basic operations, addition and multiplication, and they’d be right, too. We could go even further and say that multiplication is just repeated addition, so addition is the one basic operation. The point of this is not to take away operations, but to narrow our focus to what is essential. We’ll take the middle ground and say that addition and multiplication are the basic operations.

Addition, the first operation most people learn, is a putting together, a shortcut for counting. You learn it with the whole numbers, but then you have to adapt the rules to deal with negative numbers and fractions and decimals. Once you’ve encountered the integers, however, subtraction can be defined as adding the opposite, a special case of addition. Multiplication is a shortcut for repeated addition, but so useful that we’ll call it a separate operation, and again adjust the rules for integers and rational numbers. When your world of numbers includes fractions, division can be defined as multiplying by the reciprocal, and so a special case of multiplication.

Other Operations

There are other operations used in arithmetic, the principle ones being powers and roots. A power is a shortcut for repeated multiplication. The base is the number being multiplied, and the small raised number, called an exponent, tells how many times it appears as a factor. Taking a root is the opposite, or inverse, of raising to a power. If 2, raised to the third power, is 8, then the third root of 8 is 2.

DEFINITION

A power is a way to tell how many times a number should be used in repeated multiplication. The number to be multiplied is the base of the power, and the small raised number that tells how many times to use it is called the exponent. A root is the opposite operation of a power, a way of undoing a power.

Roots are one of the places where you encounter irrational numbers, and where mathematicians began to think about those imaginary numbers. There are gaps between integers that are perfect squares. You know that 3² = 9, so 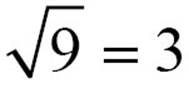, and 4² = 16, so 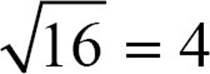, but what about all the numbers between 9 and 16? They have square roots, and those square roots are numbers between 3 and 4, but when you try to look for them, you realize they can’t all be written as fractions. They’re not rational numbers.

Properties

The operations of addition and multiplication work within certain rules or properties. Most of these properties talk about one operation on one set of numbers. We’ll look at the real numbers and investigate each property.

The closure property says that all your work with the real numbers stays in the real numbers. Whenever you add two real numbers, you get a real number. If you multiply two real numbers, you get a real number. Every time you perform the operation on two members of the set, you get another member of the set. The real numbers are closed for addition and for multiplication.

THINK ABOUT IT

The closure property doesn’t seem to say much until you look at where it doesn’t work. For example, the integers are not closed for division. Two divided by three is not an integer. The positive numbers are not closed under subtraction.

The associative property says that grouping can be changed without changing the result. The associative property for addition of real numbers tells you that (3 + 8) + 4 = 3 + (8 + 4). The associative property for multiplication of real numbers says that the product (2 × 5)× 7 is the same as the product 2 × (5 × 7). In a series of the same operation, you can choose where to start. You don’t have to start at the left and move to the right if you see an easier move.

The commutative property guarantees that when you add two or more real numbers, or multiply two or more real numbers, the result is the same, even if the order of the numbers is changed. The sum of 6 + 8 is the same as 8 + 6 and multiplying 9 × 4 gives the same answer as 4 × 9. In addition or multiplication, a change in the order of the numbers will not change the outcome.

It’s important to remember that addition and multiplication are commutative but subtraction and division are not. 5 – 1 is not the same as 1 – 5 and 8 ÷ 2 doesn’t equal 2 ÷ 8. However, you can think of subtraction as adding the opposite. For example, 5 – 1 is 5 + -1 and that is equal to -1 + 5. The same is true for division. Change a division like 8 ÷ 2 to 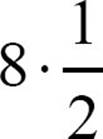and that’s equal to .

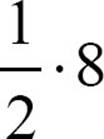The identity property assures that there is some number in the set that leaves other numbers unchanged when you operate with it. For the real numbers under addition, this number is 0. For the real numbers under multiplication, this number is 1. Adding 0 or multiplying by 1 changes nothing. Zero is the additive identity. One is the multiplicative identity.

Following on the heels of the identity property, the inverse property says there is a way to get back to the identity element. For every number in the set, except 0, there is an opposite, or additive inverse, you can add to get to the additive identity of 0. For every real number except 0, there is a reciprocal, or multiplicative inverse, that you can multiply by to produce an answer of 1, the multiplicative identity.

THINK ABOUT IT

You could say that zero is its own opposite because 0 + 0 = 0, but usually zero is considered a special case, neither positive nor negative. Zero has no reciprocal. There is no number that multiplies with zero to make 1, or for that matter, any number but zero.

There is one property that involves both addition and multiplication, and that’s the distributive property for multiplication over addition. This property looks at adding two real numbers and then multiplying the result by a third real number, for example, 8(5 + 2). The property tells you that you can produce the same answer by multiplying each of the addends by the multiplier first, and then adding. In other words, 8(5 + 2) = 8(5) + 8(2).

ALGEBRA TRAP

Be aware that you can’t distribute addition over multiplication. 4 + (5 × 3) does not equal (4 + 5) × (4 + 3).

Closure, identity, and inverse are not properties that are talked about a lot, but they guarantee that the system of arithmetic operates logically. They make it possible to undo arithmetic that’s been performed, and that will be crucial for algebra. The associative, commutative, and distributive properties pop up regularly in day-to-day arithmetic. You can use them to rearrange a problem to make the arithmetic simpler, and you’ll continue to do that in algebra.

DEFINITION

The properties of the number system include:

Closure: Adding or multiplying two numbers of the set gives us another number in the set.

Associative: (a + b) + c = a + (b + c), (ab)c = a(bc)

Commutative: a + b = b + a, ab = ba

Identity: Adding 0 or multiplying by 1 leaves a number unchanged.

Inverse: Every number, except 0, has an opposite and a reciprocal. Adding the opposite brings you back to 0. Multiplying by the reciprocal gets back to 1. Zero is its own opposite but has no reciprocal.

Distributive: c (a + b) = ca + cb

CHECK POINT

Choose all the correct answers for each question.

1. 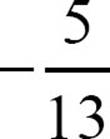is

a) an integer

b) a rational number

c) an irrational number

d) a real number

2. 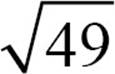is

a) an integer

b) a rational number

c) an irrational number

d) a real number

3. 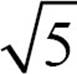is

a) an integer

b) a rational number

c) an irrational number

d) a real number

4. 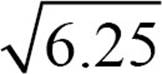is

a) an integer

b) a rational number

c) an irrational number

d) a real number

Name the property illustrated by each statement.

5. − 3 ( 4 + − 4 ) = ( − 3 · 4 ) + ( − 3 · − 4 )

6. − 12 + 12 = 0

7. 93 + 26 + 17 + 14 = 93 + 17 + 26 + 14

8. 1,274 times 1,939 is a real number.

9. 17 · 1 = 17

10.

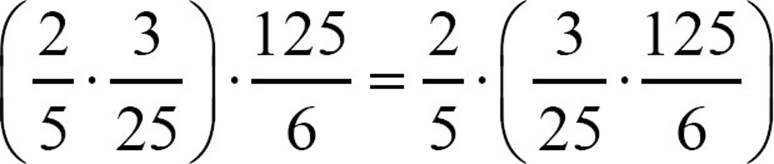
Integers and Absolute Value

Working with integers is not terribly different from the arithmetic of whole numbers; in fact, the arithmetic of fractions is much more to learn. What you’ve learned about operations with integers carries over to all real numbers, so reviewing that information is worthwhile.

What Are the Integers?

Integers are positive and negative whole numbers and zero. If you imagine the whole numbers placed along a line to the right of zero, evenly spaced, and then hold a mirror at zero, the reflection in the mirror will give you a picture of the negative numbers.

DEFINITION

The integers are the whole numbers and their opposites. All the spaces between the integers are filled with rational and irrational numbers.

This “through the looking glass” quality of the negative integers can make it confusing when you’re trying to talk about size, order, and comparison. Remembering that numbers to the left are smaller will help with order and size. When you’re trying to compare two numbers, the one on the left on the number line is smaller. For arithmetic operations, separating the absolute value of a number from its sign can sometimes be helpful.

Absolute Value

The absolute value of a number is the value of the number without its sign. The number 12 and the number -12 have the same absolute value. Both are 12 units away from zero, but 12 is to the right of zero and -12 to the left.

DEFINITION

The absolute value of a number is its distance from zero without regard to direction.

Addition (and Subtraction)

Addition and subtraction can be understood as moving right or left along the number line, but once that understanding is in place, you’ll want some shortcuts so that you don’t have to build a giant number line to do your taxes. Separating the absolute value of a number from its sign helps to express the simple version of those shortcuts.

To add two numbers with the same sign, add the absolute values and keep the sign. A positive number plus a positive number is a positive number, and a negative plus a negative is a negative.

To add two numbers with different signs, subtract the absolute values and take the sign of the number with the larger absolute value. You have competing forces, one pulling right and one pulling left. They’ll partially cancel each other out, but the one with the larger absolute value will win.

When you add 12 + −7, the absolute values are 12 and 7, and you subtract them to get 5. The 12 is the bigger absolute value, so the sign of the 12 is the sign of the answer: 12 + -7 = 5. When you add 4 + -9, the absolute values are 4 and 9, and the answer will be negative, because the larger absolute value is the 9, and that started out negative. 4 + -9 = -5.

If subtracting means adding the opposite (for example, to subtract 9 you actually add -9), then subtracting signed numbers becomes a special case of the addition rule. To subtract an integer from another number, add the opposite of the integer and follow the rules for addition.

Multiplication (and Division)

Multiplication is repeated addition. If you add 7 + 7 + 7, you’re adding three 7s, and that’s the multiplication problem 3 × 7 = 21. Applying that logic to adding several negative numbers, like -4 + -4 + -4 + -4 + -4, you have 5 × -4 and you can see that it gives you -20.

You can use the idea of repeated addition to see that the product of two positive numbers is a positive number, and that the product of a positive and a negative is negative. What happens when you multiply a negative number by a negative number? One way to think of such a problem is to see each of the negative numbers as -1 times a positive number; for example, −6 · −8 is ( −1·6)·(−1·8). Then you can use the associative and commutative properties to rearrange.

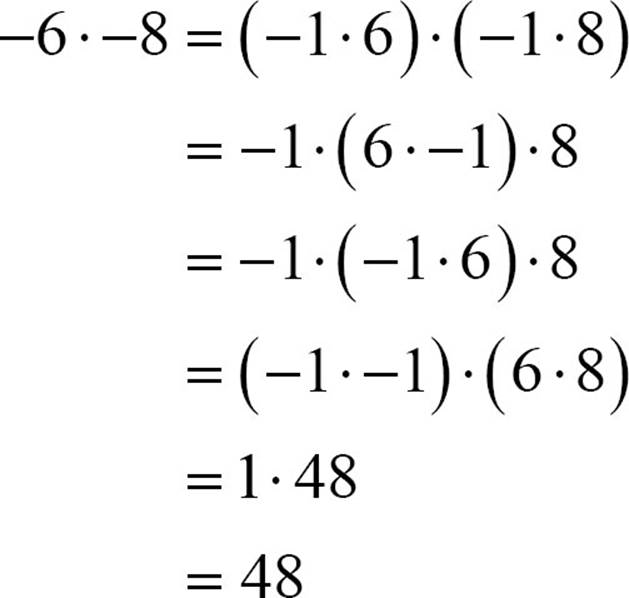
THINK ABOUT IT

Some of the properties of real numbers can also help explain why the product of two negative numbers must be positive. You know that adding a number and its opposite will give you 0, and you know that 0 multiplied by any number, positive or negative, is 0. Let’s say your number is 5. 5 + -5 = 0. Now multiply by a negative number like -3. By the distributive property, -3 ( 5 + - 5 )= - 3 · 5 + - 3 · - 5 = - 15 + - 3 · - 5, but the final answer must be 0, so the - 3 · - 5 must be positive 15.

The result of multiplying a negative number by a negative number is a positive number. Two negatives, like two positives, give a positive. That lets us formulate two rules.

1.  To multiply two numbers with the same sign, multiply the absolute values, and make the product positive.

2.  To multiply two numbers with different signs, multiply the absolute values and make the product negative.

Since division is defined as multiplying by the reciprocal, the same sign rules apply. To divide by an integer, multiply by its reciprocal, following the rules for multiplication.

CHECK POINT

Simplify each expression. Use the associative and commutative properties whenever they’re helpful.

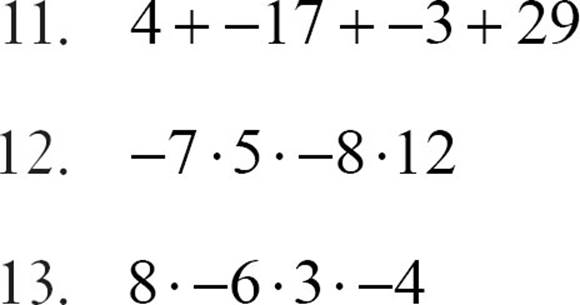
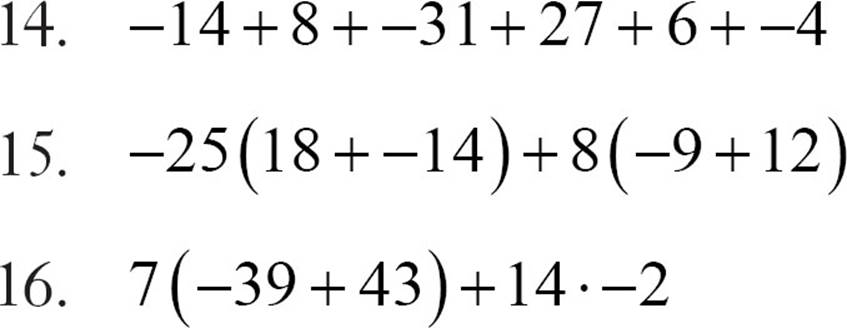
These expressions involve real numbers that are not all integers, but the same rules apply.

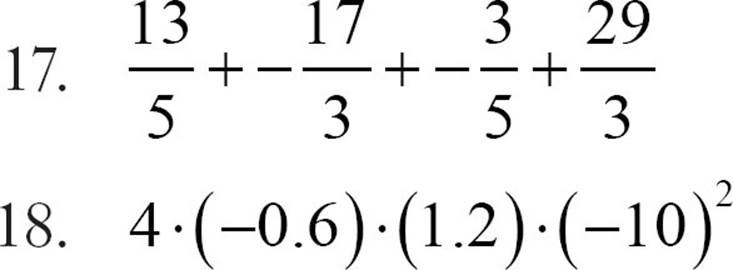
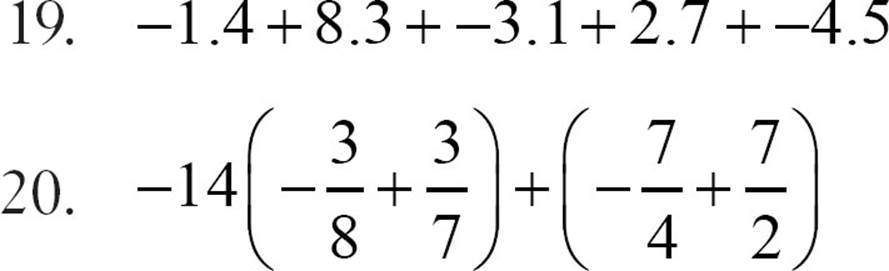
Properties of Exponents

The basic operations of addition and multiplication are themselves shortcuts. Addition is a shortcut for counting, and multiplication is a shortcut for repeated addition. One of the other common operations, raising a number to a power, is a shortcut for repeated multiplication.

Meaning of Exponent

The product 2·2·2 can be represented using an exponent as 2³. The 2, the number actually being used as a multiplier or factor, is called the base. The small raised number, called an exponent, tells you how many 2s to multiply. The base and the exponent together form a power. The power 5⁴ is shorthand for multiplying four 5s. The power 8² tells you to use 8 as a factor twice.

DEFINITION

The official name for the operation of raising to a power is exponentiation.

Powers show up frequently in algebra, so it’s useful to have some shortcuts for dealing with them. There are three essential rules that will make it easier to operate with powers, but it’s important to state, right up front, that these rules only apply to powers with the same base. If you need to multiply 2³ by 5², you’ll just have to work out that it’s 8 times 25 and end up with 200. There’s no shortcut when the bases are different. Notice, too, that there’s no shortcut for addition or subtraction of powers. You just need to work those out.

TIP

When you raise a negative number to a power, be sure to put the negative number in parentheses before putting the exponent on. This is especially important when using a calculator. If you mean (−3).(−3), write (−3)². If you write −3², your reader (or your calculator) will see that as −(3.3).

Multiplying Powers

When you multiply powers of the same base, you’re joining two statements of repeated addition. If you multiply 7³·7⁵, you’re saying (7·7·7)·(7·7·7·7·7). That’s all multiplication, so you can wrap the whole job into one exponent. You want to multiply a total of eight 7s, so you can write 7⁸. Because the bases are the same, you just condense two sets of 7s, three in one and five in the other, into one set of eight.

To multiply powers of the same base, keep the base and add the exponents.

Dividing Powers

To understand the rule for dividing powers, you need to think about fractions for a moment. If you write a quotient of two powers of the same base, say 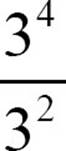, you have a fraction whose numerator and denominator have factors in common: 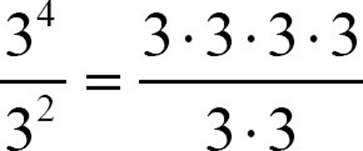. In that situation, you have the right to simplify the fraction by removing factors equivalent to 1. 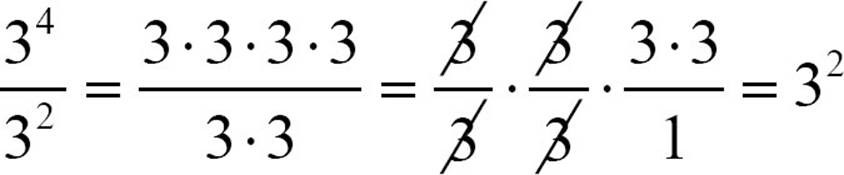. Each 3 in the denominator cancels a 3 in the numerator, leaving 4 – 2, or two 3s.

To divide powers of the same base, keep the base and subtract the exponents. Subtract the exponent of the denominator from the exponent of the numerator.

Raising a Power to a Power

Raising a power to a power is repeated multiplication of repeated multiplication, and that interpretation will give us the shortcut. To raise 2⁵ to the third power means to use 2⁵ as a factor three times. So (2⁵)³ = (2⁵)·(2⁵)·(2⁵). You could write out exactly what that means and then count up how many 2s you have, or you could use the rule for multiplying powers of the same base. (2⁵)³ = (2⁵)·(2⁵)·(2⁵)=2⁵⁺⁵⁺⁵ = 2¹⁵. (That’s 32,768, by the way.)

To raise a power to a power, keep the base and multiply the exponents.

Zero Exponents and Negative Exponents

Because an exponent tells you how many times to use the base as a factor, most of the exponents you encounter are positive integers. But applying the rules for exponents can lead to some results that might be puzzling.

When you apply the rule for dividing powers to a problem like 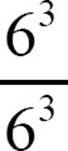, you find yourself with 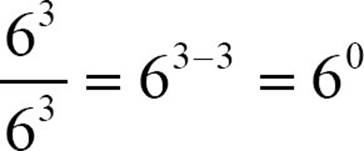. To understand what it means to use a factor zero times, you go back to the problem and apply some basic arithmetic. When you divide 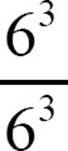, you’re dividing a number 6³=216 by itself, and a number divided by itself equals one. That gives us a definition of a zero exponent.

Any non-zero number to the zero power is one.

THINK ABOUT IT

Why do we say “any non-zero number”? The definition of a zero exponent relies on division, and division by zero is impossible.

The division rule can produce another unexpected result. If you divide 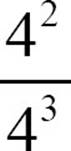, the division rule says 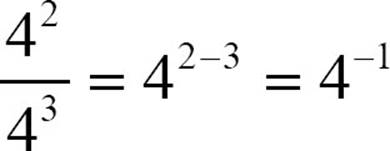. To make sense of that, go back to basic arithmetic. 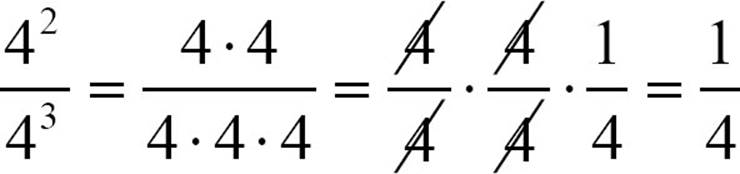. Is it a coincidence that you wind up with 1 over the base of the power? Not at all. There are more 4s in the denominator than the numerator; in this case, the denominator has one extra 4.

A base to the -1 power is equivalent to the fraction with a numerator of 1 and a denominator equal to the base.

If you have more than one extra factor in the denominator, for example, 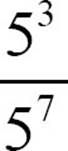, instead of getting your base to the -1 power, you’ll get some other negative power, in this case, 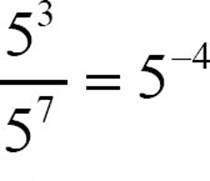. Look again at the arithmetic to see what that means. 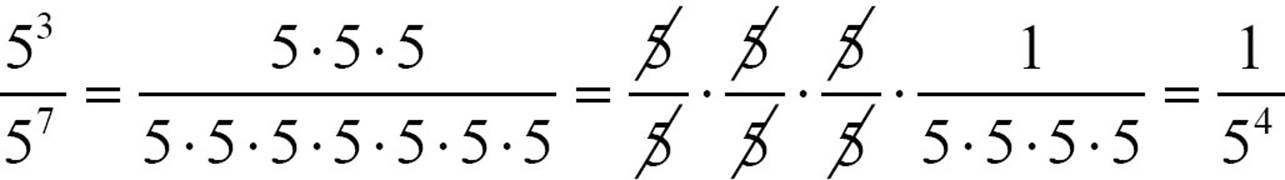. An exponent of -4 indicates the fourth power of the base will be the denominator, with a numerator of 1.

A negative exponent on a non-zero base represents a fraction with a numerator of 1 and a denominator of the base raised to the corresponding positive power.

Fractional Exponents

You might be wondering, now that we’ve looked at zero and negative exponents, if there can be fractional exponents. The answer is yes, and the short explanation is that fractional exponents represent roots.

Imagine you have a power, like 8³. Taking the third root of 8³ would undo the third power and get you back to 8. If there is an exponent that represents the third root, it should be true that raising 8³ to that power equals 8, or (8³)^?=8¹. The power of a power rule says you should multiply those exponents, so 3 times what number will give you an exponent of 1? The missing number is , so an exponent of represents the third root.

The third root of 8³ would be written as 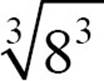. The little 3 in the crook of the radical, the index, says you’re undoing the third power. (If there’s no index, it’s a square root.) The exponent version would be 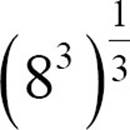. Both the radical version and the exponent form are equal to .

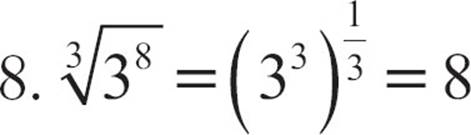Any exponent of the form 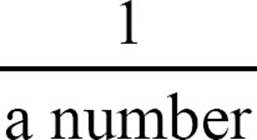represents a root. The number in the denominator of the fraction tells you what root.

CHECK POINT

Use the rules for exponents to simplify each expression.

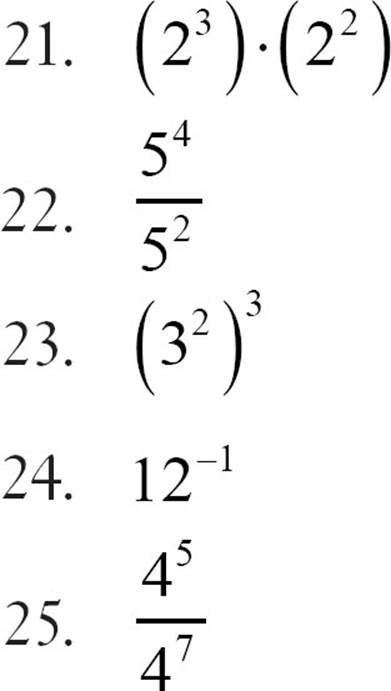
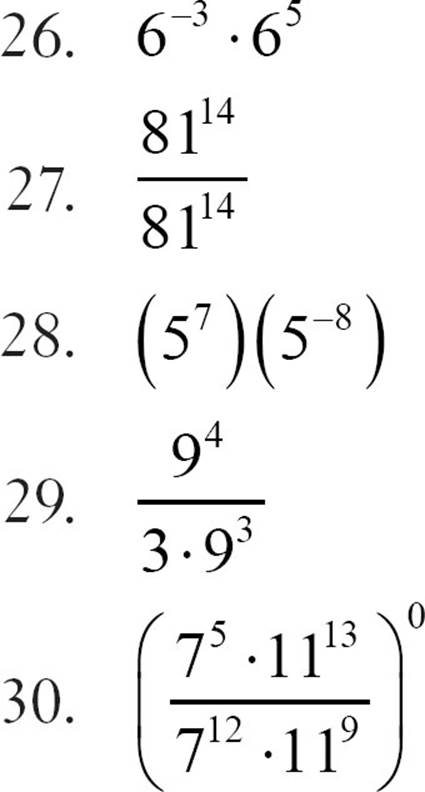
Until now, we’ve been primarily focusing on one operation at a time: addition, or multiplication, or exponentiation. However, you don’t usually encounter operations one at a time. You’re often asked to add and multiply, or find powers and subtract, or do all of those in the same problem. How do you keep it organized?

Order of Operations

Faced with the problem 16 + 5·12, it’s important that everyone agrees on the order in which the arithmetic should be done, or we could get different answers to the same problem. Working left to right might seem logical, and would give you 16 + 5·12 = 21·21 = 252, but if you thought that the multiplication was easier, and did that first, you’d get 16 + 5·12 = 16 + 60 = 76. They can’t both be right, so which one is? The answer is an agreement that multiplication will come before addition. (The correct answer to the problem above is 76.)

The agreed-upon order of operations states that multiplication and division are done first, from left to right, followed by addition and subtraction, from left to right. However, if there are grouping symbols, such as parentheses, those come before anything else. If the problem had been written (16 + 15) × 12, you would do the operation in parentheses first.

DEFINITION

The order of operations is an agreement about the sequence in which arithmetic will be performed. Expressions in parentheses are simplified first, then powers. Multiplication and division are done as met from left to right, and finally addition and subtraction, from left to right.

The associative and commutative properties allow us to rearrange an addition or a multiplication to make the arithmetic easier. When addition and multiplication appear in the same problem, there are often places to apply the distributive property. The computation 5(16 + 24) + 8(92 + 18) can be done by following the signal from the parentheses and adding first.

5(16 + 24) + 8(92 + 18) = 5(40) + 8(110)= 220 + 880 = 1,080

But if you find it easier, you can distribute the multiplication.

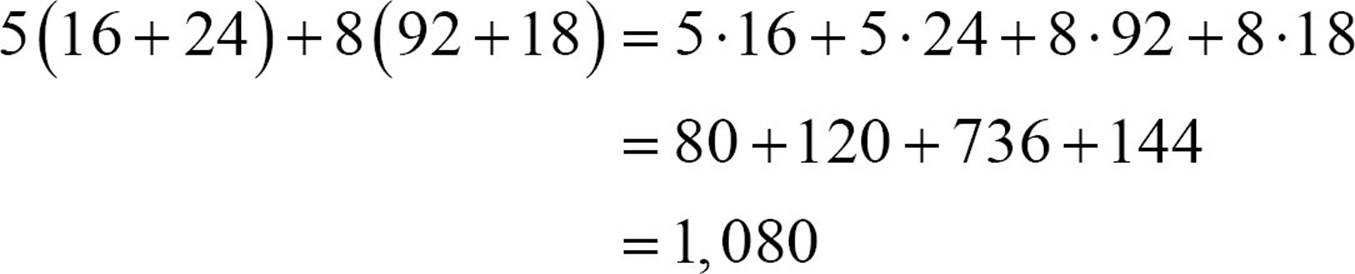
You also have the option to mix your strategies. 5(16+24) is not too hard to calculate by either method, but I know what 5·16 and 5·24 equal, so I’d probably distribute there. On the other hand, 8(92+18) is much easier if I add first.

Just as multiplication, a shortcut for repeated addition, gets done before addition, exponents, the symbol for repeated multiplication, need to be handled before multiplication or addition. Do exponents, multiplication, and addition, in that order, unless parentheses say otherwise. What about subtraction and division? Those are defined as special cases of addition and multiplication, respectively, so subtraction gets done with addition and multiplication with division. That leaves us with a rule for the order of operations that you can remember as PEMDAS: parentheses, exponents, multiplication (and division), addition (and subtraction).

CHECK POINT

Simplify each expression, following the order of operations.

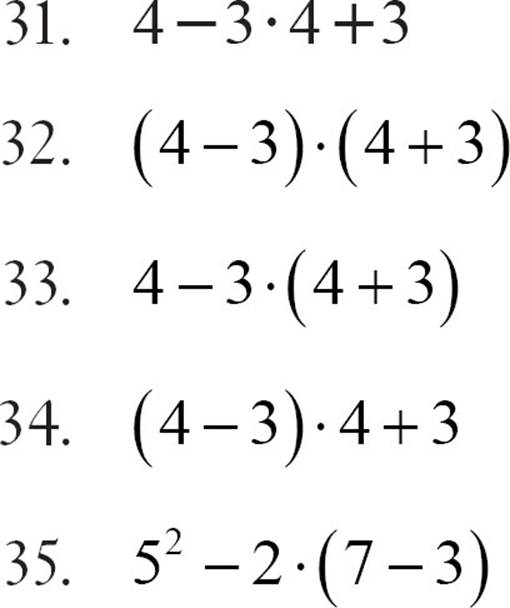
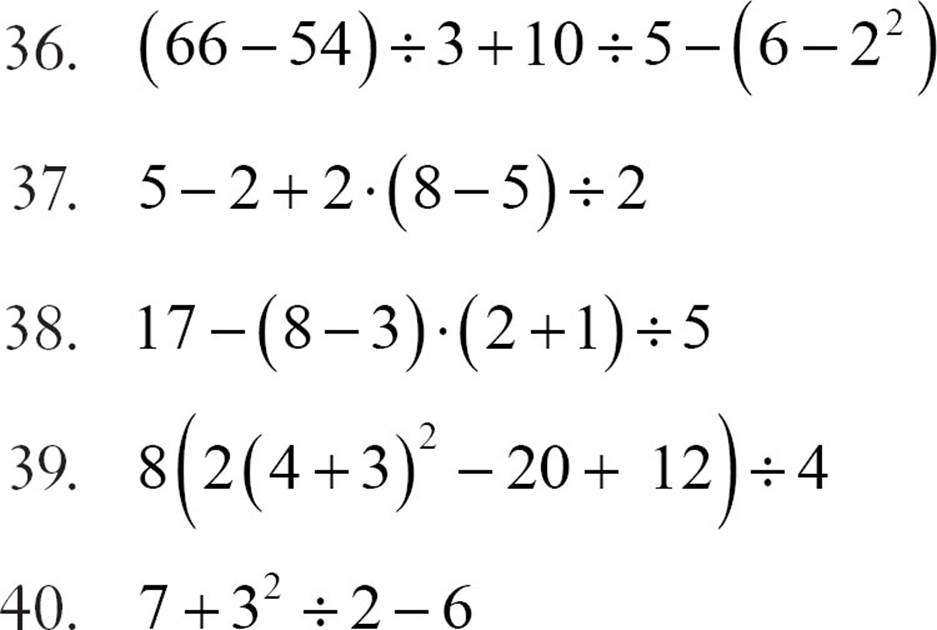
A clear understanding of arithmetic is the foundation you need to begin your study of algebra. Working with unknowns will require you to think carefully not only about what kind of arithmetic you need to do but also about how that arithmetic works and why.

The Least You Need to Know

·  Arithmetic in the real number system is governed by the associative, commutative, distributive, identity, inverse, and closure properties.

·  The sign rules for operating on integers hold true for all real numbers: rational and irrational.

·  Shortcuts for multiplying, dividing, and finding powers of powers simplify work with exponents

·  The order of operations—parentheses, exponents, multiplication and division, addition and subtraction—governs arithmetic, and is represented by the acronym PEMDAS.