Idiot's Guides: Algebra I (2015)
Part I. Introduction to Algebra
Chapter 2. Variables and Expressions
In This Chapter
![]()
· Understanding and using variables
· Identifying and combining like terms
· Simplifying expressions with the distributive property
· Multiplying variable expressions
What makes a detective story interesting is that some important piece of the story is unknown. There wouldn’t be much need for a detective if we already had all the facts. That element of the unknown is also what distinguishes algebra from arithmetic.
In arithmetic, you have all the numbers and you know what operations need to be performed; you just have to do the math. When there’s a missing piece—a number you don’t know or one that keeps changing—you need algebra to solve that mystery. In this chapter, we’ll bring variables into arithmetic, and investigate what changes and what stays the same when one (or more) of the numbers you’re working with is unknown.
Variables and Expressions
A variable is any symbol used to stand for an unknown number or for a number that keeps changing. It can be as simple as a blank to fill in, as in 4+___ = 7, but in algebra, variables usually take the form of letters. If you order a new jacket that costs $45 but have to pay for shipping, you could use a variable like x to stand for the shipping charge, and the total cost of your purchase would be $(45 + x). If you find out what the shipping charge is, you can do the math and know exactly what the total will be, but until you have that information, a variable lets you talk about it even though one piece is unknown.
![]()
DEFINITION
A variable is a letter or other symbol that takes the place of an unknown number.
Because a variable takes the place of a number, you can write phrases and sentences using variables as you would numbers. Making the transition from words to symbols like numbers, variables, and operations can take some practice. It’s a lot like translating from one language to another. When you first try it, you translate word by word, but as you become more comfortable with the language, you’re able to read the whole phrase or sentence and say the same thing in the new language.
If you write, in words, “six plus nine equals fifteen,” you can translate that to the symbols 6 + 9 = 15. If you write the words “six plus some number equals fifteen,” you can use a variable, like n, to represent “some number” and the sentence becomes 6 + n = 15. The translation is word by word. Six becomes 6, plus becomes +, and so on.
Whenever you’re trying to translate, it’s helpful to understand the grammar of the language. In algebra, numbers and variables are nouns and operation signs like + and × are conjunctions that tie the numbers and variables together. In English, you learn to distinguish between a phrase, such as “the weather forecast for Monday” and a sentence, such as “The weather forecast for Monday is sunny.” The key difference between them is the verb. In algebra, equal signs and inequality signs are the verbs. If you write 6 + n, that’s a phrase made up of two nouns and a conjunction: “six and a number.” In algebra, that’s called an expression. If you write 6 + n = 15, the equal sign acts as a verb. Your sentence is “six plus some number is 15.” Equations and inequalities are the sentences of algebra.
Language provides many different ways to say the same thing, and employing that variety can make writing more interesting. The symbolic representations used in math are less diverse, however, and as a result many different sentences translate to the same set of symbols. The sentence “six plus nine equals fifteen” could also be “the sum of six and nine is fifteen” or “nine more than six is fifteen” or “six increased by nine is fifteen.” All those sentences would translate to 6 + 9 = 15.
It’s difficult, if not impossible, to list all the different ways to express the same mathematical statement, but here are some common ones.
Because addition and multiplication are commutative, the order of the numbers can be changed. x + 4 and 4 + x are equivalent. For subtraction and division, which are not commutative, take the order of the numbers from the sentence. The quotient of a and b is ![]() . The quotient of b and a is
. The quotient of b and a is ![]() . The difference of x and y is x – y but the difference of y and x is y – x.
. The difference of x and y is x – y but the difference of y and x is y – x.
![]()
ALGEBRA TRAP
There is one exception to the rule for subtraction. When it says something like “9 less than a number,” you subtract 9 from the number. If you say it with numbers rather than variables, it’s easier to see. A number that’s two less than five is clearly three, or 5 – 2, not 2 – 5. If you want a number that’s 2 less than x, it’s x – 2, not 2 – x.
Of course, the context of the question can change the way the information is presented to you. If you’re looking for two numbers that add to 100 and one is greater than the other by 25, you could call one number x and the other x + 25. Then your sentence is x + x + 25 = 100. If you paid for two lamps plus a $25 delivery fee, and your total bill was $100, that would also be x + x + 25 = 100. Different situations (in words) can lead to the same set of symbols.
![]()
CHECK POINT
Write an equation for each sentence, using the specified variable.
1. The product of -4 and a number x.
2. A number y increased by 18.
3. The quotient of a number z and 8.
4. The product of 9 and a number x, decreased by 3.
5. Nineteen more than the product of -3 and a number x.
6. The difference of two numbers, a and b, multiplied by -5.
7. A number x is subtracted from 19.
8. Twice a number x increased by 4 is 8 more than a number y.
9. George bought 3 hot dogs and spent $1.50 for a drink. His total bill was $12. (Use h for the price of one hot dog.)
10. One number is 15 more than another and their sum is 42. (Use n for the smaller number.)
To talk intelligently about algebra, we need to be speaking the same language, using the same words to mean the same things. We’ve defined a variable as a symbol, usually a letter, which takes the place of a number. Let’s build from there.
Factors, Terms, and Expressions
When you multiply, each number or variable is a factor and the result is a product. When you multiply two numbers, you can find the product and give the result as a single number. When one or more of the factors are variables, you can’t arrive at a single number because you don’t know the value of the variable, but you can express the multiplication in a compact fashion. Multiplying the number 7 and the variable x can be written as 7x. Multiplying x times x, or any variable by itself, can be condensed by using an exponent. x · x = x2. Multiplying two different variables, like x and y, just becomes xy.
![]()
DEFINITION
A product is the result of multiplying. Each of the numbers or variables multiplied is a factor.
A collection of factors, whether numbers or variables or both, that are connected only by multiplication is called a term. A term may contain a power because exponents are a shortcut for multiplication, but not addition. When you add two or more terms, you create an expression. Expression is a more general word. Terms are expressions, and sums, differences, and quotients of terms are also expressions.
In writing, you build sentences from phrases, and the phrases are made up of words. In algebra, the sentences are equations or inequalities. The equal signs and inequality signs act like verbs. Expressions are phrases and terms are like words.
![]()
DEFINITION
An expression is any mathematical calculation. An expression containing numbers and variables combined only by multiplication is called a term.
The expression –3x is a term with two factors: -3 and x. Technically, each of these factors is a coefficient, the -3 is the numerical coefficient and the x is the variable coefficient. If you look at the roots of the word coefficient, it means things that work together. The -3 and the x work together to make the term.
The expression 5x2 is a term. It has a coefficient of 5. The variable is squared, which means the term is really 5 · x · x, so technically it has three factors.
The expression 5x2 + – 3x (or 5x2 – 3x) is the sum of two terms.
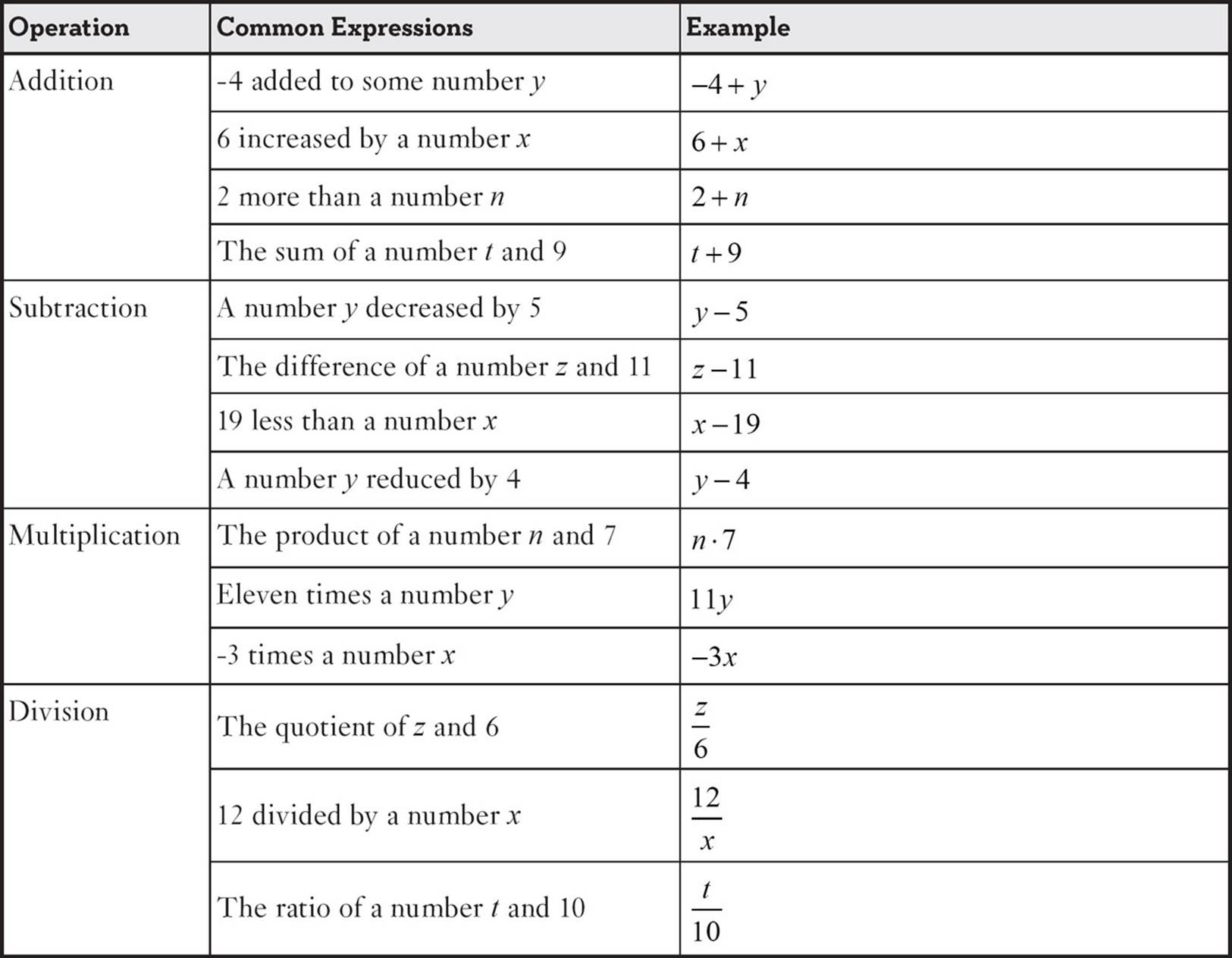
The expression 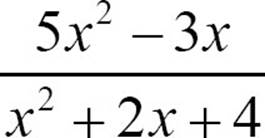 is a quotient of two expressions. The numerator has two terms and the denominator has three terms.
is a quotient of two expressions. The numerator has two terms and the denominator has three terms.
![]()
DEFINITION
The word coefficient usually refers to the numerical part of a term. Technically, a term is made up of a numerical coefficient and a variable coefficient.
![]()
CHECK POINT
Identify the number of factors in each term.
11. 3x
12. –6y2
13. 23xy
14. –48x3y2
Identify the number of terms in each expression.
15. x2 + 3x –8
16. t – 2
17. 6x2
18. 9x2 – 4x
19. 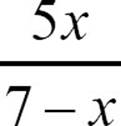
20. 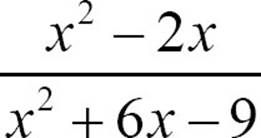
Arithmetic with Variables
When you add, each of the numbers or variables being added is called an addend and the result is a sum. At first, it might seem that arithmetic with variables would be impossible. How can you add numbers you don’t know? Although you can’t assign a number to x + x, you can say that it’s two of the same number, and that means x + x = 2x. You still can’t say what it’s worth until you know what x stands for, but you have a simpler way to represent the addition.
![]()
DEFINITION
Each of the numbers or variables in an addition problem is called an addend, and the result is called a sum.
You add variable terms that are like, terms that have the same variable and same exponent, by just adding their coefficients. When you write a term like 5x, 5 times x means five copies of the number you don’t know. It means x + x +x + x + x. If you add 3x to that, you’re adding another three copies of that unknown number, x + x + x. That will give you a total of eight of those unknown numbers, eight x’s or 8x.
![]()
DEFINITION
Like terms have the same variable and the same exponent.
As long as the addends are just copies of the same variable, all you’re really doing is counting up how many you have. When you start to add terms, like 6x and –8x, you’ll want a simpler method than just counting. As long as the terms are like, that is, terms with the same variable and same exponent, you can just add the coefficients and keep the variable parts the same.
In addition to combining terms with the exact same variable part, you can also combine the numbers that have no variable part. These terms, which are just numbers, are called constant terms or simply constants.
![]()
DEFINITION
Constants are simple terms containing only numbers and no variables.
Combining Like Terms
You’ll want to simplify expressions whenever you can. You could write the expression 5x – 1 + 3x + 5 – 2x + 8 + 9x – 4, which is the sum of eight terms. That expression can be simplified, however. The simplified result will be much easier to write and definitely easier to work with. You can use the associative and commutative properties to rearrange, and then do as much of the arithmetic as you can without knowing what number x stands for. The rule to remember is that you can only combine terms that have identical variable parts.
5x – 1 + 3x + 5 – 2x + 8 + 9x – 4
(5x + 3x – 2x + 9x) + (– 1 + 5 + 8 – 4)
15x + 8
Simplifying an expression as complex as 5x – 1 + 3x + 5 – 2x + 8 + 9x – 4 requires using the associative and commutative properties to group like terms together. You wouldn’t usually show every single step in that rearrangement, but it’s worthwhile to think about them once or twice. Working left to right, your first step would be 5x – 1 but those are unlike, so use the associative property to regroup. (5x – 1) + 3x + 5 – 2x + 8 + 9x – 4 = 5x + (– 1 + 3x) + 5 – 2x+ 8 + 9x – 4. Use the commutative property to change the order. 5x + (3x – 1) + 5 – 2x + 8 + 9x – 4. Regroup again. (5x + 3x) – 1 + 5 – 2x + 8 + 9x – 4. Now you can combine the like variable terms, and the constants that follow. The more terms, the more regrouping and switching required.
Remember to think of subtraction as adding the opposite. When you see 5x – 1, you want to think of that as 5x + – 1. When you think of subtraction as adding the opposite, it lets you use the associative and commutative properties to rearrange the expression for convenient simplifying.
![]()
CHECK POINT
Simplify each expression by combining like terms.
21. (x + 3) + (9 + x)
22. (2x – l) + (3x + 9)
23. (x2 + 5) + (x2 + 6x) + (8x + 3)
24. (2x + 7) + (8x + 4) + (–x2 – 1)
25. (2x – 4) + (6x + 1) + (3 – x)
26. (y + 5) + (2y – 9) + (4y + 10) + (y – 6)
27. (8t – 4) + (–t – 1) + (13t – 7) + (– 2t – 9)
28. (x2 + 4) + (–x2 – 1) + (– 3 – 5x) + (10x + 9)
29. (3x2 + 2x + 4) + (x2 – 3x + 10)
30. (4x2 – 5x – 6) + (9 + 7x – 4x2)
When you multiply, each number or variable is a factor and the result is a product. Multiplication with variable expressions can have different looks: one term times one term, one term times an expression with more than one term, and multiplication of two expressions that both have more than one term. All the different cases break down to multiplying one term by one term, and doing that means multiplying the coefficients, multiplying the variables, and applying the rules for exponents when necessary. For example, 4x · – 2x2 = (4 · – 2) · (x · x2) = –8x3.
The Distributive Property
When we talked about the basic properties of arithmetic, we said that the distributive property allows you to choose to add and then multiply, or multiply and then add. You can do 6(5 + 3) either as 6(5 + 3) = 6(8) = 48 or as 6(5 + 3) = 6(5) + 6(3) = 30 + 18 = 48. It’s up to you to choose.
In algebra, when you’re dealing with unknowns, the distributive property gives you a chance to simplify expressions that present an obstacle. When you face – 4(x + 7), you can’t add first. The x and the 7 are unlike terms and can’t be combined, and you don’t know the value of x. But thanks to the distributive property, you can multiply first.
− 4(x + 7) = (−4)x + (−4) (7) = − 4x − 28
When you use the distributive property with a multiplier that’s a constant, you just need to be careful about rules for signs. When you use the distributive property with a multiplier that includes a variable, you’ll also need to remember the rules for exponents, primarily the rule for multiplying powers. To multiply 2x(x2 + 3x + 5), first distribute the 2x.
2x(x2 + 3x + 5) = 2x (x2) + 2x (3x) + 2x (5)
Then do each individual multiplication, remembering that x = x1 and that when you multiply powers of the same base, you keep the base and add the exponents.
2x (x2 + 3x + 5) = 2x (x2) + 2x (3x) + 2x (5)
= (2 x2 · x2) + (2 · 3 · x1 · x1) + (2 · 5 ·x)
= 2x3 + 6x2 + 10x
![]()
ALGEBRA TRAP
Remember that terms with the same variable but different exponents are unlike terms. An x is not the same as an x2. If x stands for 7, x2 stands for 49, definitely not the same thing. Like terms must have the exact same variable part, including the exponent.
When a negative number or a term with a negative coefficient needs to be distributed over an expression, it’s important to pay attention to the signs. In the expression −3x(x2 − 5x + 2), you need to multiply each of the three terms in the parentheses −3x by , and that means you’ll need to be thinking carefully about the sign of each resulting term. −3x · x2 will be negative, specifically, − 3x3. −3x −5x will be positive and −3x · 2 will be negative. You should get −3x (x2 −5x + 2) = −3x3 + 15x2 − 6x.
When you see just a negative sign in front of an expression in parentheses, you’re actually seeing an instruction to distribute -1. The effect is to change all the signs.
− (x2 − 3x − 4) = − 1(x2 − 3x − 4)
= (− 1· x2) + (−1 ·− 3x) + (− 1 ·− 4)
= − x2 + 3x + 4
Notice that the x2 became − x2, and the − 3x and the -4 both became positive.
![]()
CHECK POINT
Simplify each expression by applying the distributive property (where needed) and combining like terms.
31. 2(x − 4) + 7(x + 4)
32. − 3(y + 8) + 8(y − 3)
33. 6(2t + 5) + 9(t − 2)
34. − 7(3w − 5) + 4(w + 5)
35. x (x + 4)−(x + 4)
36. − 8x (x − 3) + 6(x − 4)
37. 5a (2a− 7)− 2(8− a)
38. − 4 y (7 − 3y)− 4(3 − 7 y)
39. 3x (2x + 3y) + 3y (2x + 3 y)
40. 2x2(x2 − 7x + 9) + 3x (x2 − 7x + 9) + 2(x2 − 7x + 9)
The distributive property will let you simplify a multiplication of one term times an expression with multiple terms, but what if you need to multiply two larger expressions? What if you need to multiply an expression with two terms by an expression with three terms?
What would you do in arithmetic if you needed to multiply 429 by 32? You’d probably arrange the numbers one under the other, and start by multiplying 429 by 2, working right to left. Then you’d put a zero on the next line to shift things over one place, and multiply 429 by 3, again right to left. Finally you’d add the two lines. This should look familiar.

You can do something similar with variable expressions. To multiply 4x2 + 2x + 9 by 3x + 2, you can:
Arrange the expressions one under another. Put the one with more terms on top.
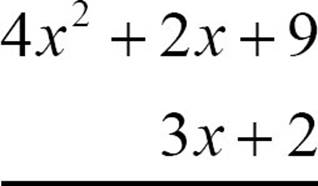
Multiply 4x2 + 2x + 9 by 2. Don’t worry about carrying. Just multiply each term by 2.
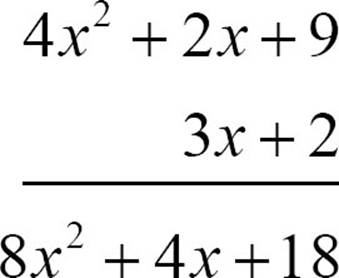
Put a zero under the 18.
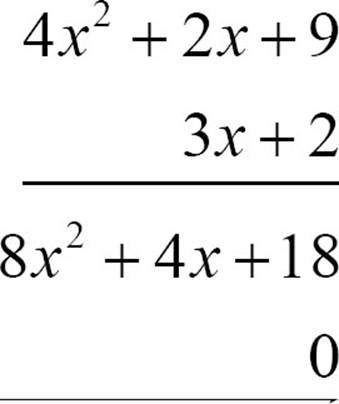
Multiply 4x2 + 2x + 9 by 3x. Remember the rules for exponents. Put the result on the same line as the zero.
4x2 + 2x + 9
Add the two lines. Like terms should already be lined up. Here’s how it should look.
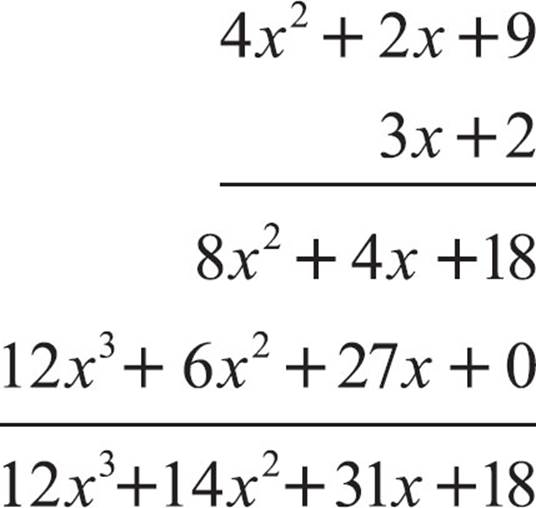
This vertical multiplication takes time and careful attention, but it follows the same pattern you used in arithmetic. You can use it to multiply any two sums of terms. As is often the case, the most common problems have a shortcut.
The FOIL Rule
You will frequently find that you need to multiply the sum of two terms by another expression that is the sum of two terms. If you do this by the vertical method, you will see that this takes a total of four little multiplications. Each term of the first expression gets multiplied by each term of the second expression.
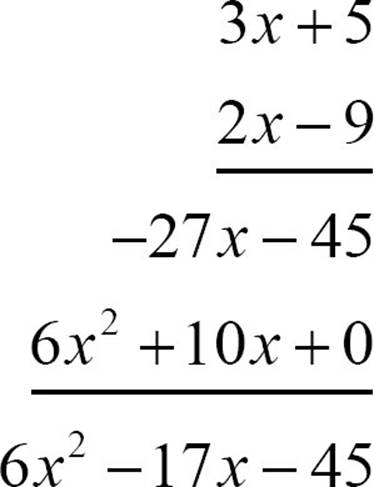
The 3x times the 2x created the 6x2.
The 3x times the -9 created the −27x.
The 5 times the 2x created the 10x.
The 5 times the -9 created the -45.
These four multiplications can be labeled using the acronym FOIL: First, Outer, Inner, Last. Start by writing the problem on one line: (3x + 5) (2x − 9).
The 3x and the 2x are the FIRST terms in each expression.
The 3x and the -9 are the OUTER ends of the problem.
The 5 and the 2x are the INNER terms.
The 5 and the -9 are the LAST terms in each expression.
Do these four multiplications and combine any like terms.
![]()
DEFINITION
The acronym FOIL stands for First, Outer, Inner, Last. It summarizes the four multiplications you need to do when multiplying two terms by two terms.
To multiply (6x + 5)(x − 3) think of it as (6x + 5)(x + − 3) and follow the FOIL rule.
First: 6x · x = 6x2
Outer: 6x ·− 3 = −18x
Inner: 5 · x = 5x
Last: 5(−3) = −15
So (6x + 5)(x − 3) = 6x2 − 18x + 5x − 15 = 6x2 − 13x − 15, once you combine the like terms −18x and 5x in the middle.
![]()
CHECK POINT
Multiply using the vertical multiplication method.
41. (2x − 7)·(x + 4)
42. (x2 + x + 2)·(x − 3)
43. (x2 + 7x + 3)·(2x + 1)
44. (2x2 − 3x − 8)·(3x − 4)
Multiply using the FOIL rule.
45. (x + 3)·(x + 2)
46. (x + 4)·(x − 2)
47. (2x + 1)·(x + 7)
48. (4x − 1)·(2x + 3)
49. (5x − 2)·(2x − 3)
50. (x2 + x)·(x − 3)
The Least You Need to Know
· You can translate phrases about unknown numbers into expressions using variables.
· Terms contain numbers and variables connected only by multiplication.
· Like terms are terms that have the same variable(s) raised to the same power.
· You can add and subtract only like terms.
· Multiply terms using the rules for exponents.
· Use the distributive property to multiply one term by an expression, the FOIL rule to multiply two terms by two terms, and set up larger expressions in the vertical arrangement.