Idiot's Guides: Algebra I (2015)
Part I. Introduction to Algebra
Chapter 3. Functions
In This Chapter
![]()
· What is a function?
· How to quickly identify functions
· Using function notation
· Constructing tables and graphs to represent functions
If you walk for an hour every day, what distance do you cover? Was your first thought “it depends”? It probably was, and rightfully so. The distance you cover in an hour depends upon the speed at which you walk, and whether you walk at a consistent speed for the entire hour. If you walk at a steady three miles per hour today, you’ll cover three miles in your hour-long walk. If tomorrow you step up your pace, you might cover four miles in the same time. The distance varies and depends on your speed. In this chapter, we’ll look at a way of representing relationships like this one with the help of variables.
Although most of the world thinks of variables as things that are unknown and need to be found, the name “variable” comes from the word vary. Variables are symbols used to represent quantities or values that vary, or are different at different times.
What Is a Function?
Before we can talk about functions, we need to define another word that has a mathematical meaning a bit different from its use in ordinary speech. In English, if you talk about a relation, you’re probably talking about a member of your family, someone who is related to you. In algebra, a relation is a pairing of the numbers from two sets.
![]()
DEFINITION
A relation is a pairing of numbers from one set, called the domain, with numbers from another set, called the range.
If set A contains the numbers {1,2,3,4,5} and set B contains {9,12,15,18,21}, you could create a relation by pairing each number from set A with a number from set B. You could make the pairs {(1,9),(2,12),(3,15),(4,18),(5,21)}, but there’s no rule that you have to go in order. You could pair them up as {(1,15),(2,9),(3,12),(4,21),(5,18)}. Any matching up of numbers from set A with numbers from set B is a relation. The first set, set A in this example, is called the domain and the second set, set B, is called the range.
If a relation is a way of relating numbers from different sets, what is a function? It sounds like it’s something that has a job to do, and often it does, but the definition of function is simpler than that. A function is a relation in which each element of the domain has only one partner from the range.
![]()
DEFINITION
A function is a relation in which each number in the domain has only one partner from the range.
Take a minute to think about that. Most people, reading that sentence, think all relations are functions, but they’re not. If the only requirement I have is to pair the numbers, I could use the sets above and do something like this: {(1,9), (1,15), (2,12), (2,9), (3,15), (3,12), (4,18), (4,21), (5,21), (5,18)}.
I’ve paired them up, but I’ve used numbers from the domain twice, so each member of the domain has two different partners. That’s a relation, but it’s not a function. If even one number from the domain gets two different partners, it’s not a function.
You might be thinking, “Okay, fine, but when does that ever really happen?” Suppose I take a set of numbers like {2,5, − 3,1.2, − 2,4,9} and I pair each of those numbers with its square. I get {(2,4), (5,25), (−3,9), (1.2,1.44), (−2,4), (4,16), (9,81)}.
That’s a function. Each number has one partner. But suppose I switch that relationship around. I take a set of numbers like {1,4,9,16} and I pair each input with a number I could square to get my input. You might at first think that my pairs would be {(1,1), (4,2), (9,3), (16,4)} but I’d be within my rights to say the pairs are {(1,1),(1,−1), (4,2),(4,−2), (9,3),(9,−3), (16,4), (16,−4)}. Each of the numbers in my domain could be paired with a negative number as well as a positive number. Pairing them with both of their square roots would not be a function.
I used rules to pair up the numbers in those examples, both for the function and the relation. Many times there is a rule that explains the pairing in a relation or a function, but not every time. Sometimes there is a rule, but it’s not obvious from the pairing. If I were to pair the ages of my family members with their social security numbers, it might look like random numbers to you even though I followed a clear rule.
Because functions often have rules, you can imagine them as machines that have a particular job to do. The numbers in the domain are called inputs, and the numbers in the range are called the outputs. Imagine the inputs going into the function machine, the machine doing its job, and then generating an output for the range.
![]()
DEFINITION
The numbers from the domain that the function works on are inputs. The numbers in the range that the function produces are outputs.

![]()
CHECK POINT
Tell whether each set of pairs forms a function. Is there a rule that determines the pairs?
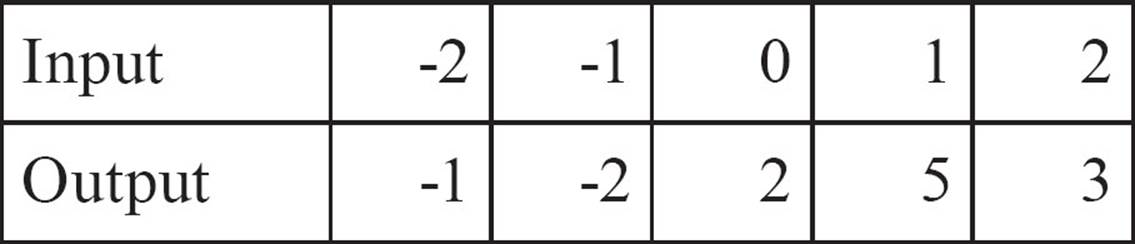
1. 
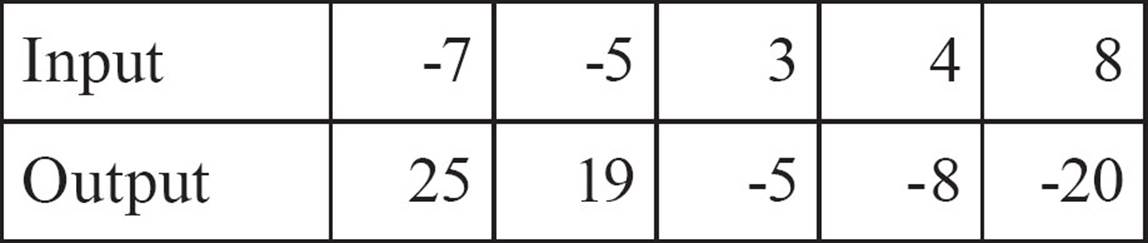
2. 
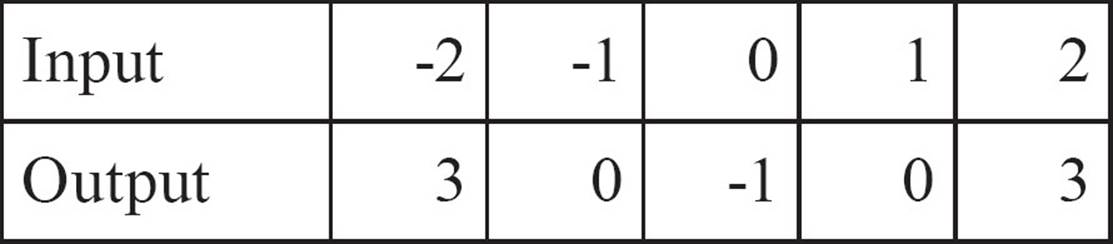
3. 
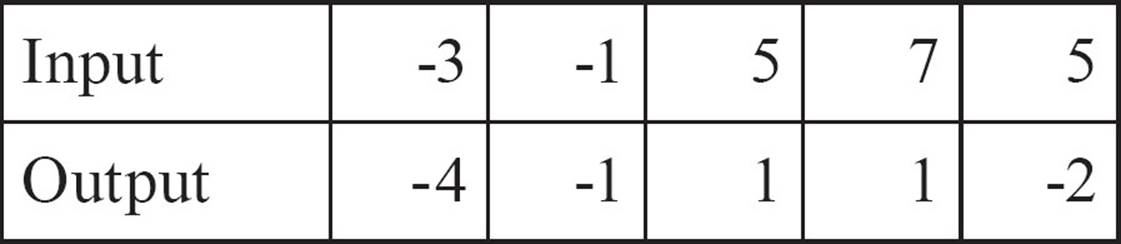
4. 
5. 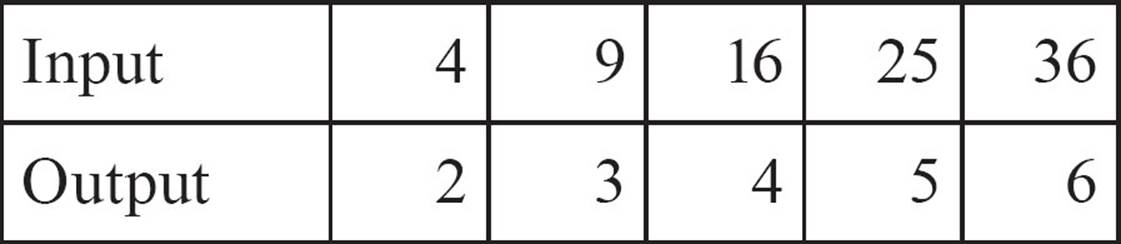
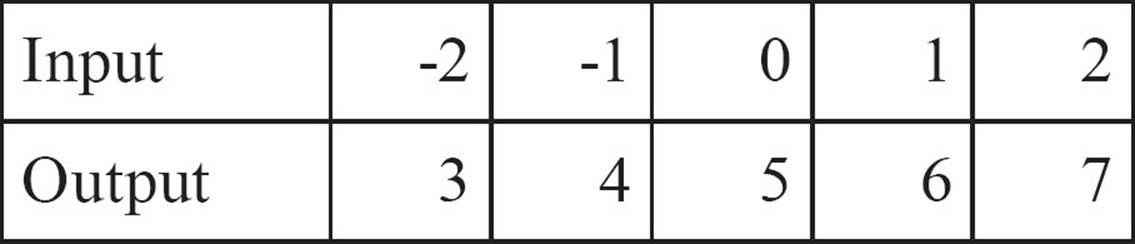
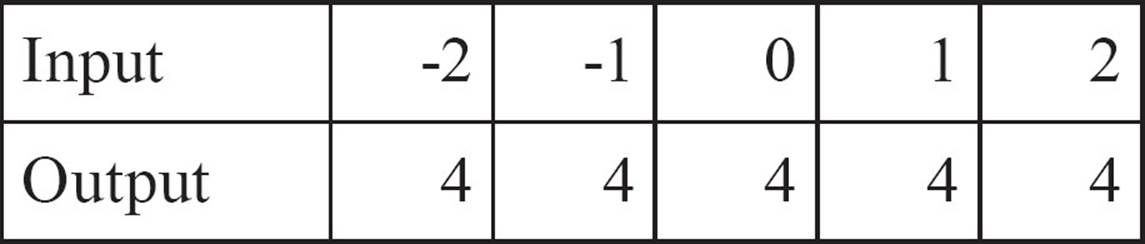
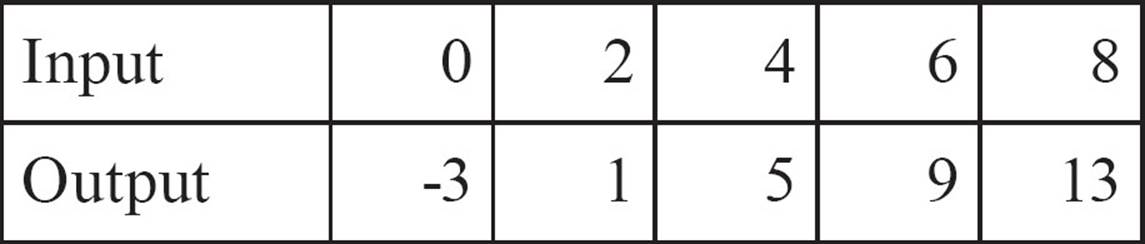
For each function, give the domain and range of the function. Does the function follow a rule?
6. 
7. 
8. 
9. 
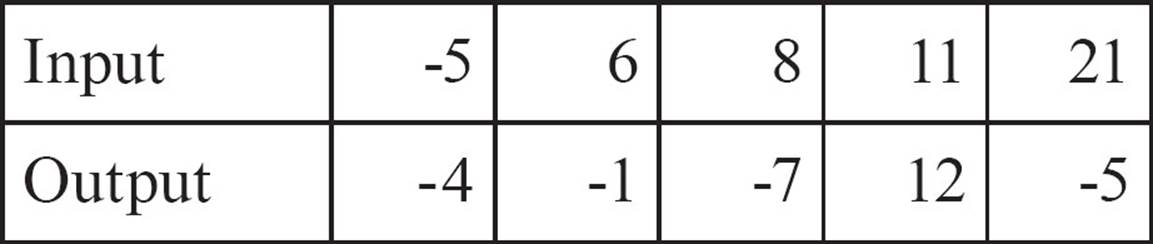
10. 
Function Notation
Functions can be specified by listing the pairs or by making a chart that shows the pairing. For large sets of numbers, this can become unwieldy, so there are other ways of communicating functions. This is where variables come in to play.
The numbers in the domain, the inputs, change. The input takes different values, so a variable can be used to stand for the input. This variable is often x, but it could be any variable. Once you choose a variable for the input, you try to express the rule for the function, if there is one, as an expression using that variable.
Suppose you want to write a simple function that matches each input with a number two units larger. You would need to say that you’re going to match each number, x, with a number of the form x + 2. You could assign a variable to stand for the outputs, perhaps y, and say the output is two more than the input, or y = x + 2. When you input 5, the function will output 7. When x = −2, y = 0.
There’s another way of writing this, called function notation, that has a couple of advantages. First, it gives the function a name. A letter, like f or g, is used to stand for the function. The variable that will stand for the inputs appears in parentheses, right after the function’s name. The notation f (x), which is read as “f of x,” says that this is a function, its name is f and the variable x stands for its inputs. Then you give the rule, if there is one, so you might write f (x) = x + 2.
![]()
ALGEBRA TRAP
Function notation puts the variable that stands for inputs in parentheses after the name of the function. Don’t confuse this with parentheses used to mean multiplication. f (x) is not f times x. It’s a function f that has inputs represented by x.
Naming the function this way makes it easier to talk and write about them. If I’m working with two functions, one that pairs inputs with two more than the input, and one that pairs inputs with their squares, having to repeat all that description every time I want to tell you about them can get tedious. If I write f (x) = x + 2 and g (x) = x2, I can just talk about f and g, and you’ll know which one I mean.
The other advantage to function notation is that it provides a compact way to say “find the output of this particular function for this particular input.” Evaluating a function means finding the output for a particular input, and function notation lets you say “evaluate this” simply. If I want you to evaluate the function f above when the input is x = 5, I can just ask you to find f (5). By writing the f, I’ve told you the name of the function you should use, and by replacing the x with 5, I’ve told you to make 5 the input. f (5) = 5 + 2 = 7. If I tell you to find g (3), you know I want you to find out what the output will be when the input to the squaring function is 3. g (3) = 32 = 9.
![]()
CHECK POINT
Given the function f(x) = 4 − 3x, evaluate each of the following.
11. f (3)
12. f (−5)
13. f (0)
14. f (−1)
15. f (−100)
Evaluate each function as indicated.
16. If g (x) = 8x − 2 find g (−4)
17. If h (x) = x2 + 5 find h (0)
18. If p (x) = x2 − 3x + 7 find p (−1)
19. If v (t) = 25 − 8t find v (5)
20. If a (t) = 9.8 find a (20)
Tables of Values
A function with a small domain can be defined by making a table showing all the pairs, as we did in the first Check Point of this chapter. If the domain of a function is large, making a table is impractical, and the function is generally defined by a rule. When a relation or a function defined by a rule needs to be evaluated for several different inputs, however, the inputs and outputs are often organized into a table of values.
![]()
TIP
A function must send each input to only one output, so you shouldn’t see repeated inputs. It’s okay for outputs to repeat, however. You may see more than one input sent to the same output. There is even a type of function called a constant function in which every input goes to the same output.
In addition to giving you a simple way to organize the pairs, a table of values also provides a quick way of determining whether the relation you’re looking at is a function. Just scan the inputs. If any input occurs more than once (and the outputs are different) the relation is not a function. If all the inputs are different, it’s a function.
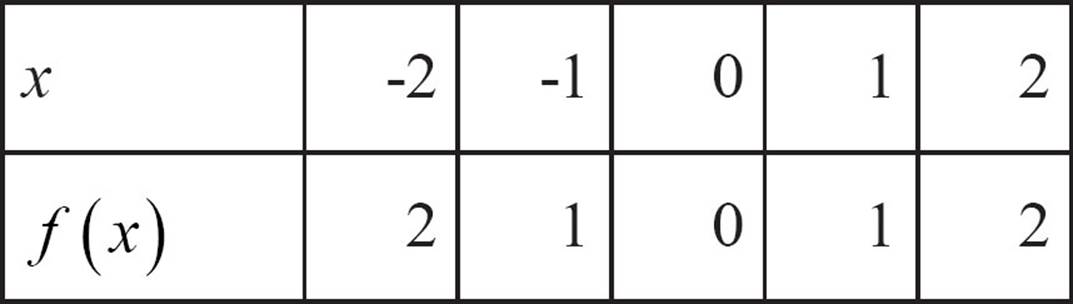
This relation is a function because each input is unique.
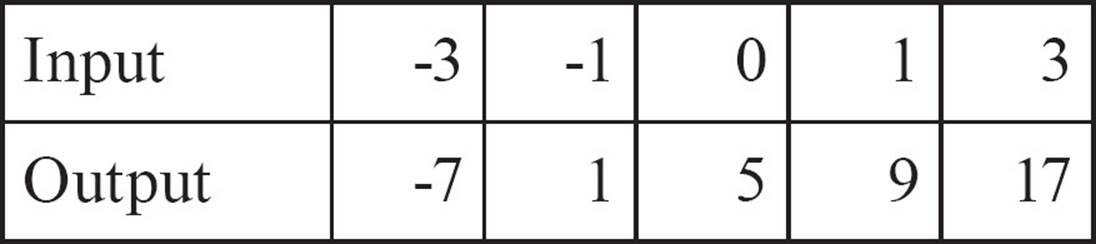
This relation is not a function because you can see that the input -1 appears twice, once with an output of 1 and again with an output of -1.

Having the inputs and outputs of a function arranged in a table of values can also help you find a rule for the function, if there is one. Make sure the inputs are in order, and if they’re not, carefully rearrange the table. Be sure to keep each output with its input. Now look at the changes in the inputs and in the outputs. The following table shows the pairs of inputs and outputs for this function, arranged with inputs in order from smallest to largest.
![]()
ALGEBRA TRAP
When you’re looking for a rule, you may tend to focus on outputs, and try to create rules that tell how to get from one output to the next. That may describe the pattern, but remember that the rule you want is how to get from an input to its output.
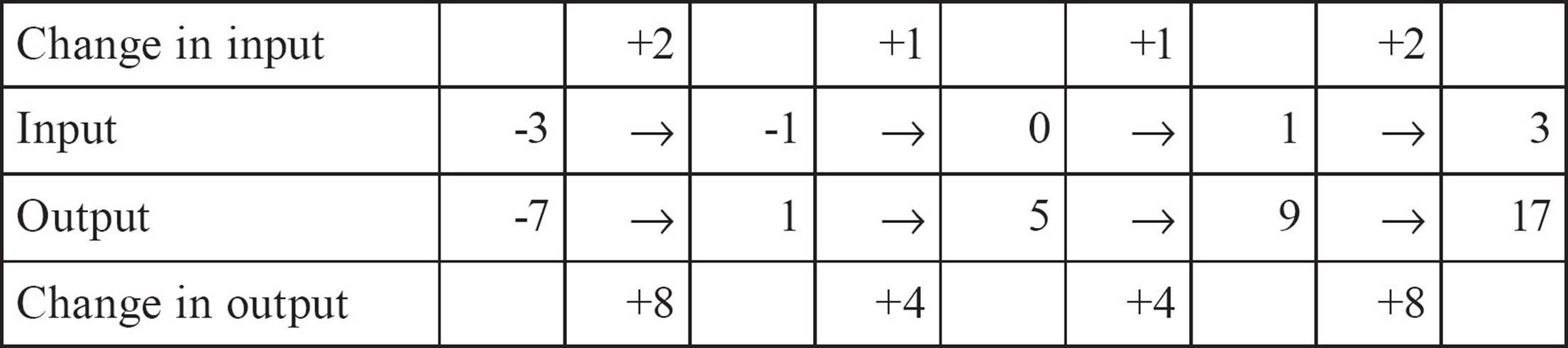
Divide each change in output by the corresponding change in input. Do all the divisions come out the same? In this example, 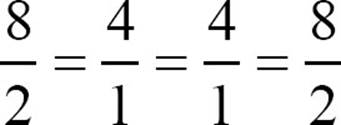 . If all those divisions come out the same, as they do here, you’re halfway to the rule. Take the result of the division, in this case 4, and multiply each input by that number.
. If all those divisions come out the same, as they do here, you’re halfway to the rule. Take the result of the division, in this case 4, and multiply each input by that number.
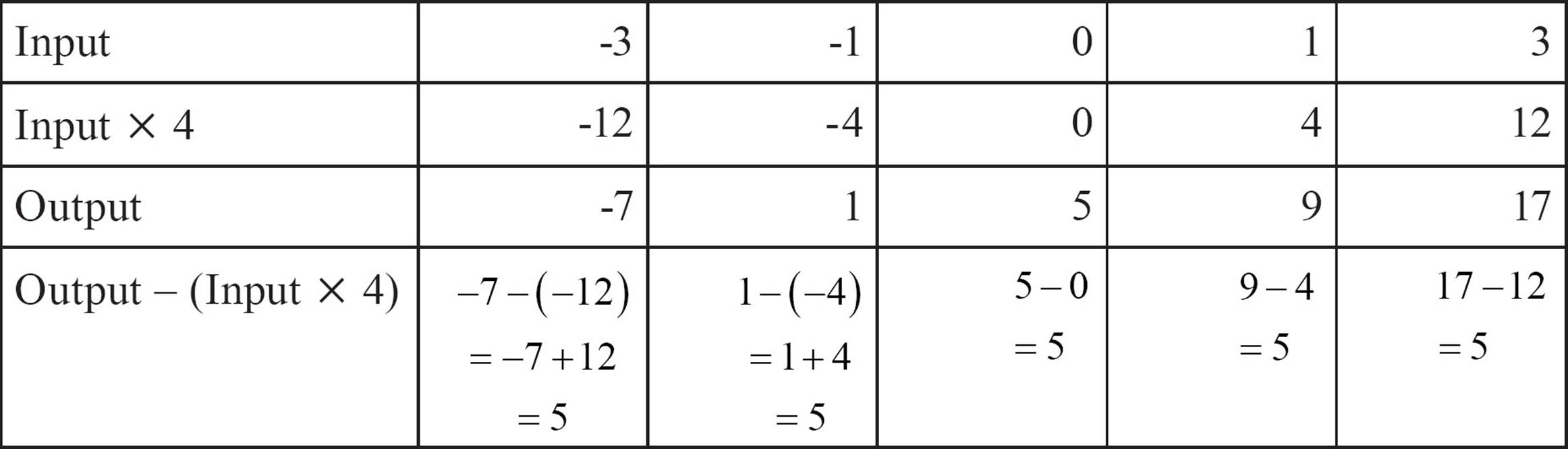
The inputs multiplied by four don’t match the outputs. In this case, they’re lower than the outputs by exactly five. The rule for this function is f (x) = 4x + 5, multiply the input by 4 and then add 5.
Here’s a table of values for another function.

When you look at the differences in the inputs and the outputs for this one, the ratios don’t all match.

Sometimes the changes don’t match because there is no rule, but don’t give up just yet. Do you notice the change in direction of the outputs? The outputs were going down, and then they went up. That change of direction is a sign that this function might have a rule that involves squaring.
Take another step by finding the changes in the changes in the outputs, like this.
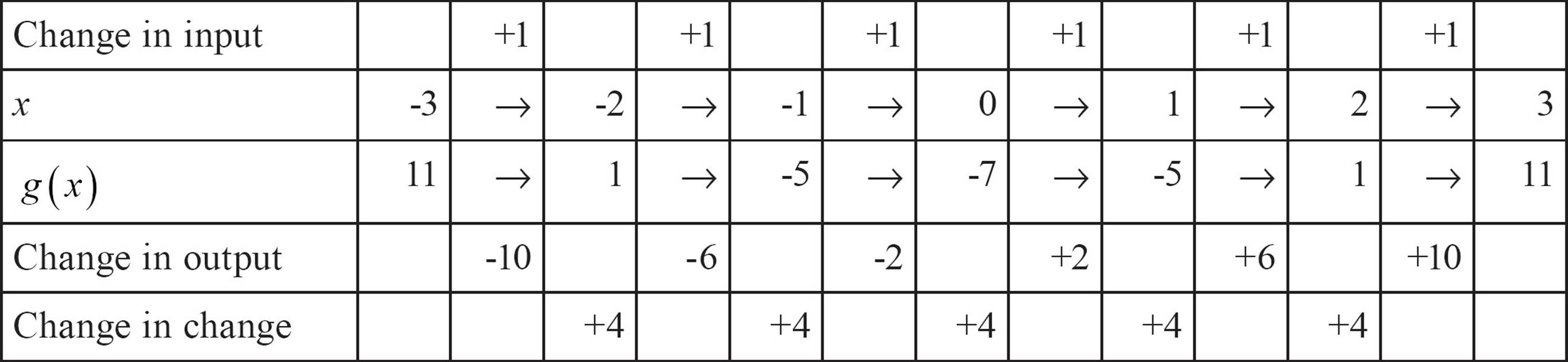
If that second set of changes are all the same, your rule will start with half that number times x2, in this case 2x2, and then you’ll need to look for what to add or subtract.
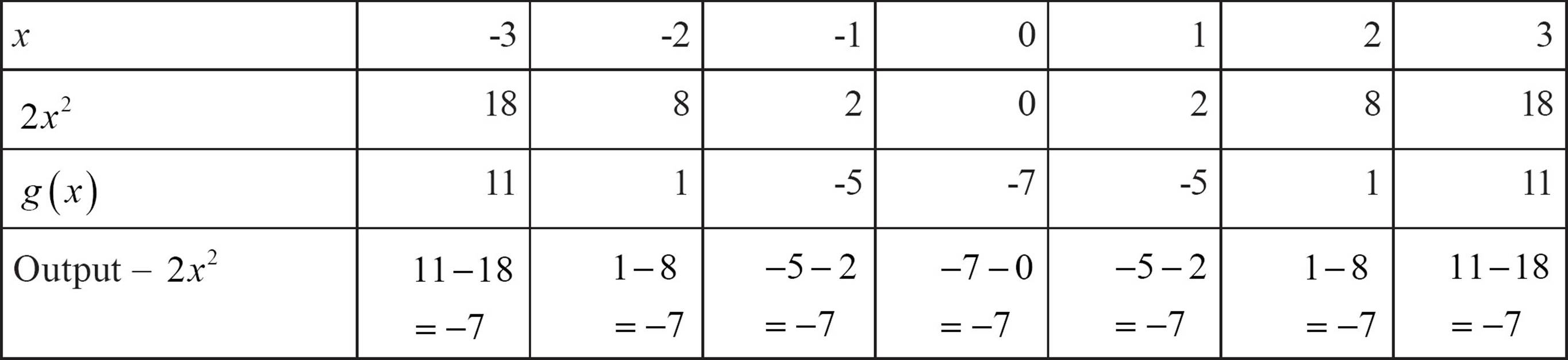
In this case, the rule will be g (x) = 2x2 − 7. This tactic won’t find every possible rule, but it will help you find many of them. Sometimes just guessing and testing will help you find a rule. Sometimes you may think there’s a rule because there seems to be a pattern, but you just don’t have the skills yet to figure out what it is. But many times, you’ll be able to express the rule for the function by following these steps.
![]()
CHECK POINT
Create a table of values for each function, using the given values for the inputs.
21. f (x) = 3x − 1 for values of x in the set {− 2,− 1,0,1,2}.
22. g (x) = 4 − x2 for values of x in the set {− 5, − 3,− 1,1,3,5}.
23. p (z) = 2z + 9 for values of z in the set {− 4, − 1,0,2,5}.
24. v (t) = t2− 1 for values of t in the set {0,1,2,3,4,5}.
25. a (t) = − 3t for values of t in the set {− 5, − 4, − 3, − 2,− 1,0}.
Each table of values below represents a function. Write a rule for the function, if possible, using function notation.
26. 
27. 
28. 
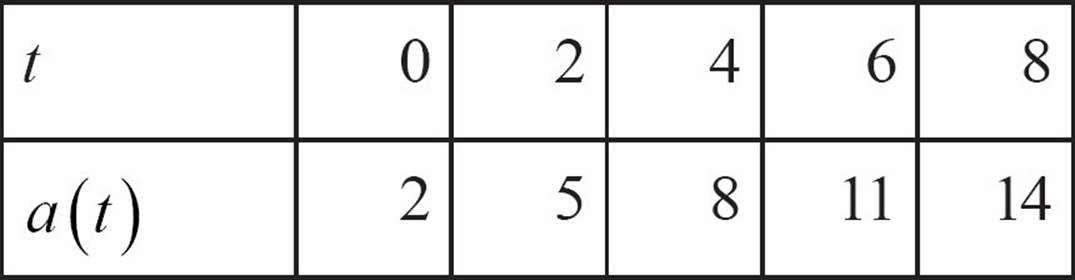
29. 
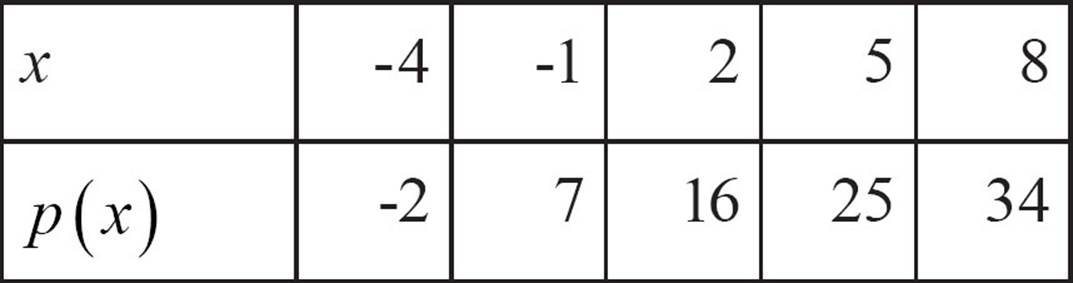
30. 
Graphs of Functions
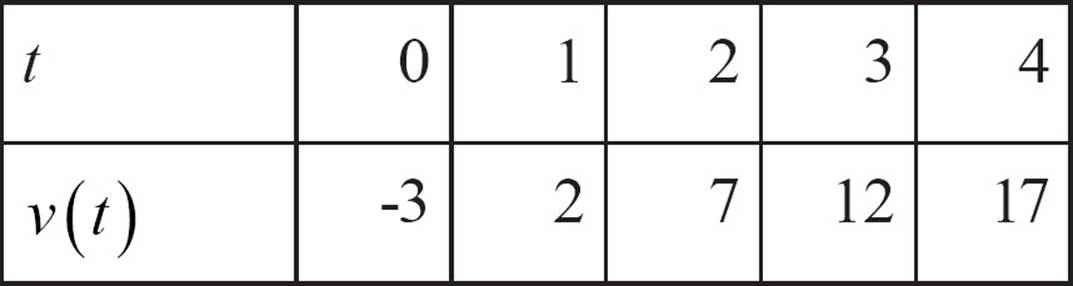
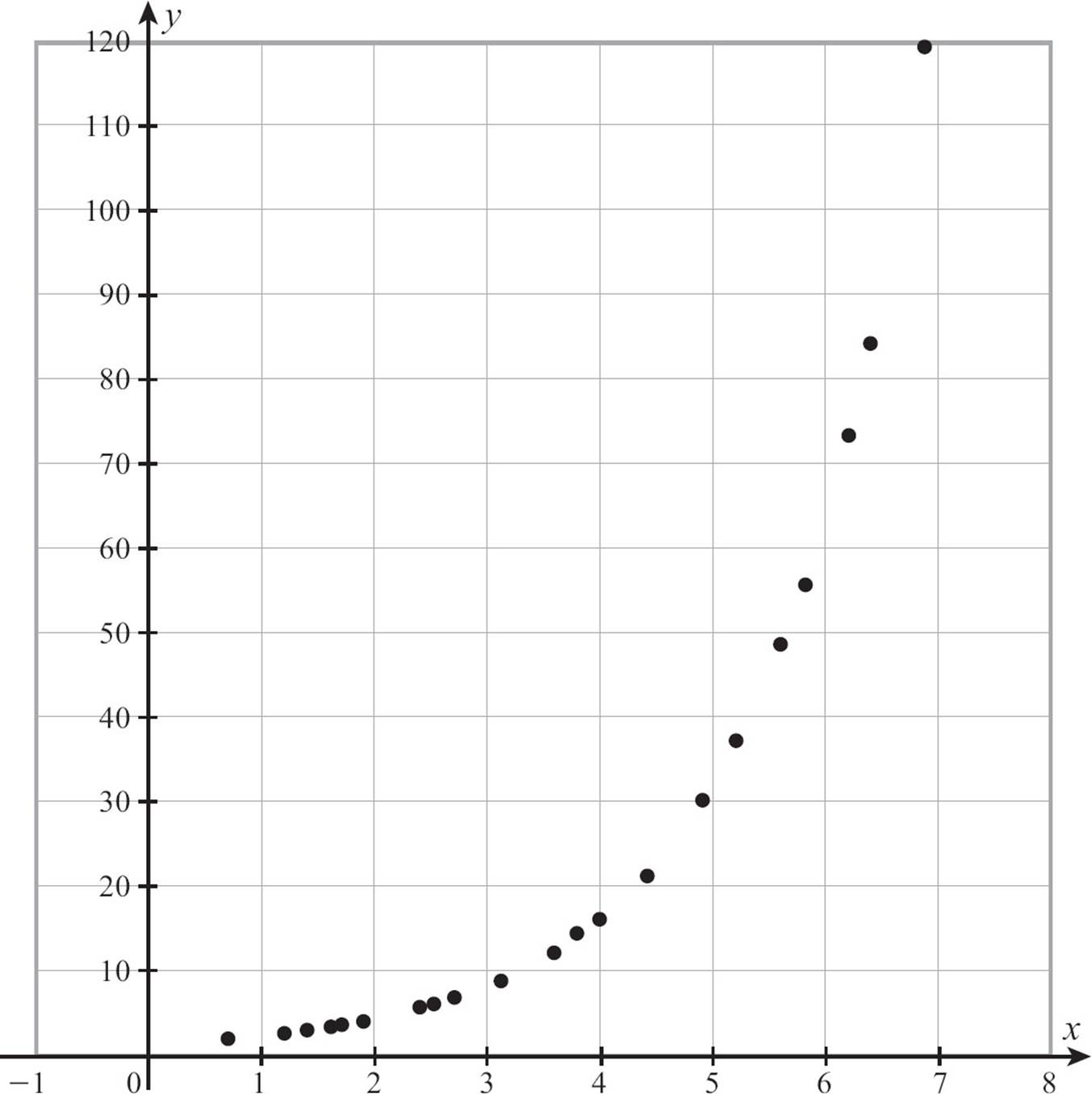
Another common way of showing a function (or a relation) is to draw a picture of the function by plotting each pair of numbers as a point in the coordinate plane. The function in the table below could be shown as five points on the plane.
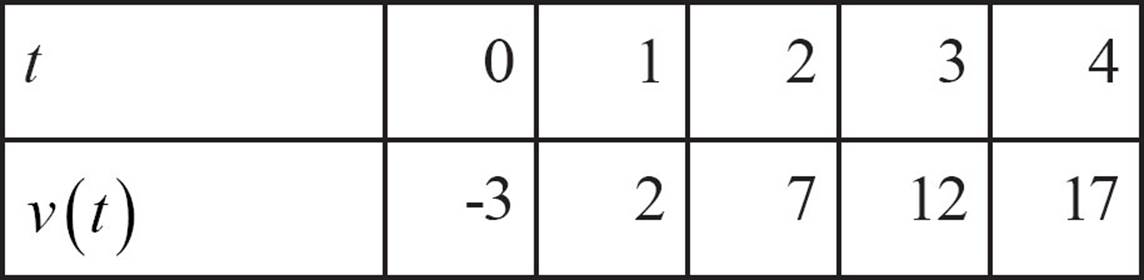
The five pairs, {(0, −3), (1,2), (2,7), (3,12), (4,17)} can be plotted as five points, with their inputs counted on the horizontal axis and their outputs on the vertical axis. The graph looks like this.
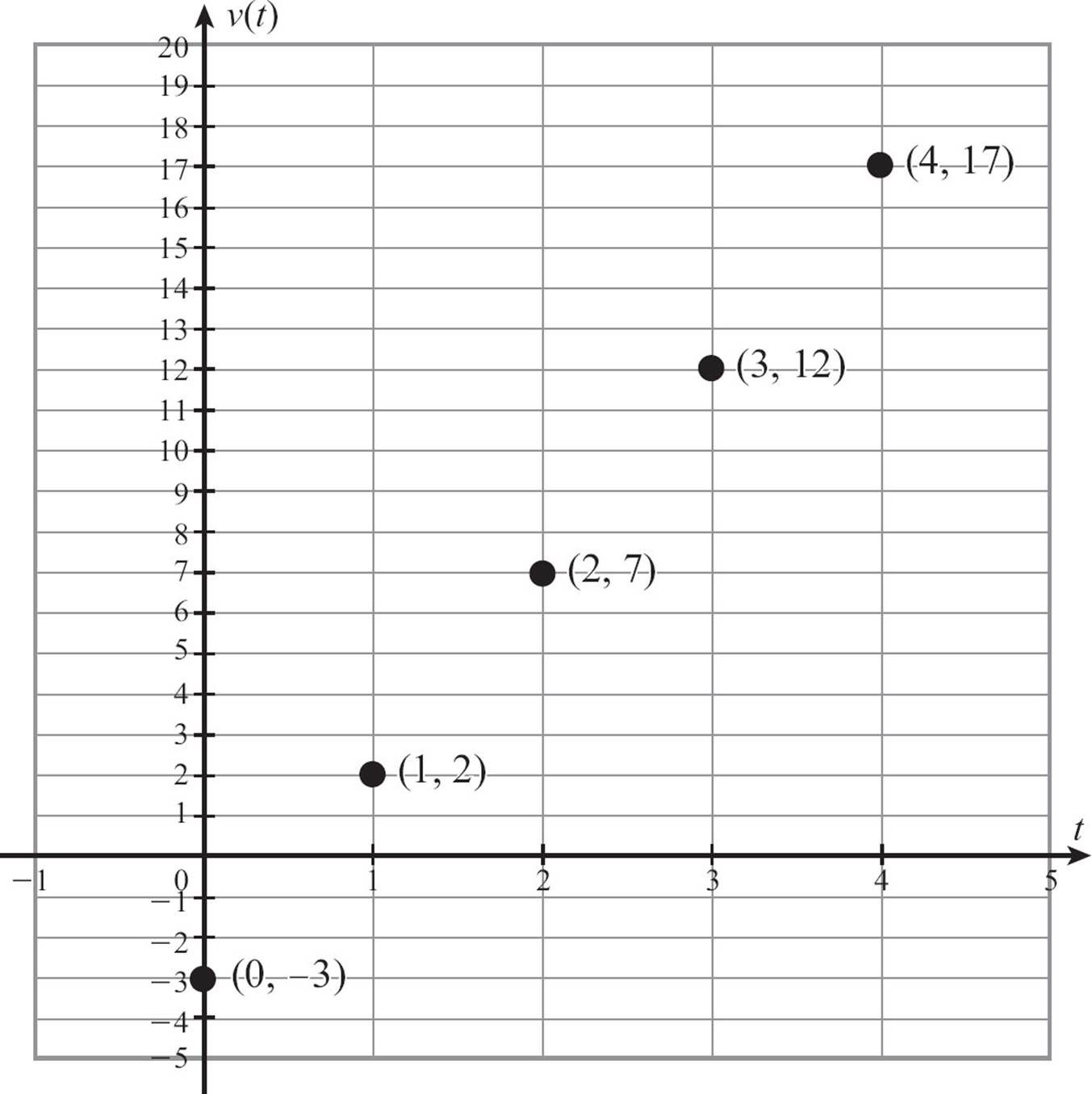
![]()
TIP
The values from the domain are always on the horizontal axis, and the values from the range are on the vertical axis.
One advantage of presenting a function as a graph is that you can often spot a pattern faster in a graph. One look at the graph above and you can see that there’s some sort of pattern or rule for this function. The points form a line. If there were no rule, the points would be just a random scattering of points.
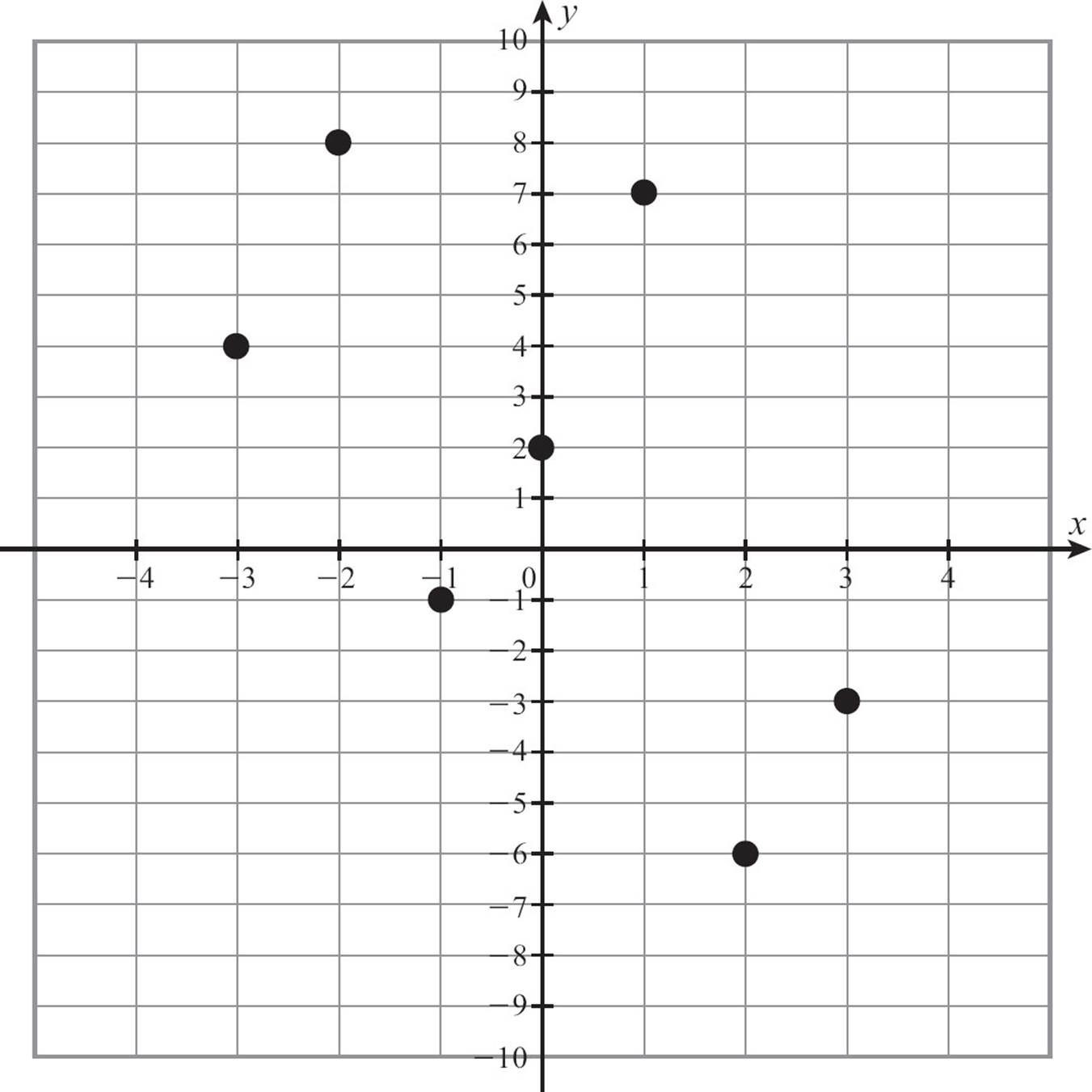
The function below does not have a rule.
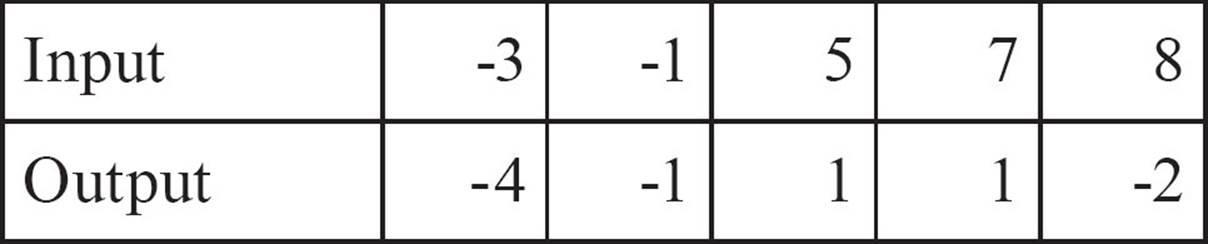
When you plot the points {(− 3,− 4),(− 1,−l),(5,l),(7,l),(8, − 2)} on a graph, you can quickly see that it’s unlikely there would be one rule that explains these pairings.
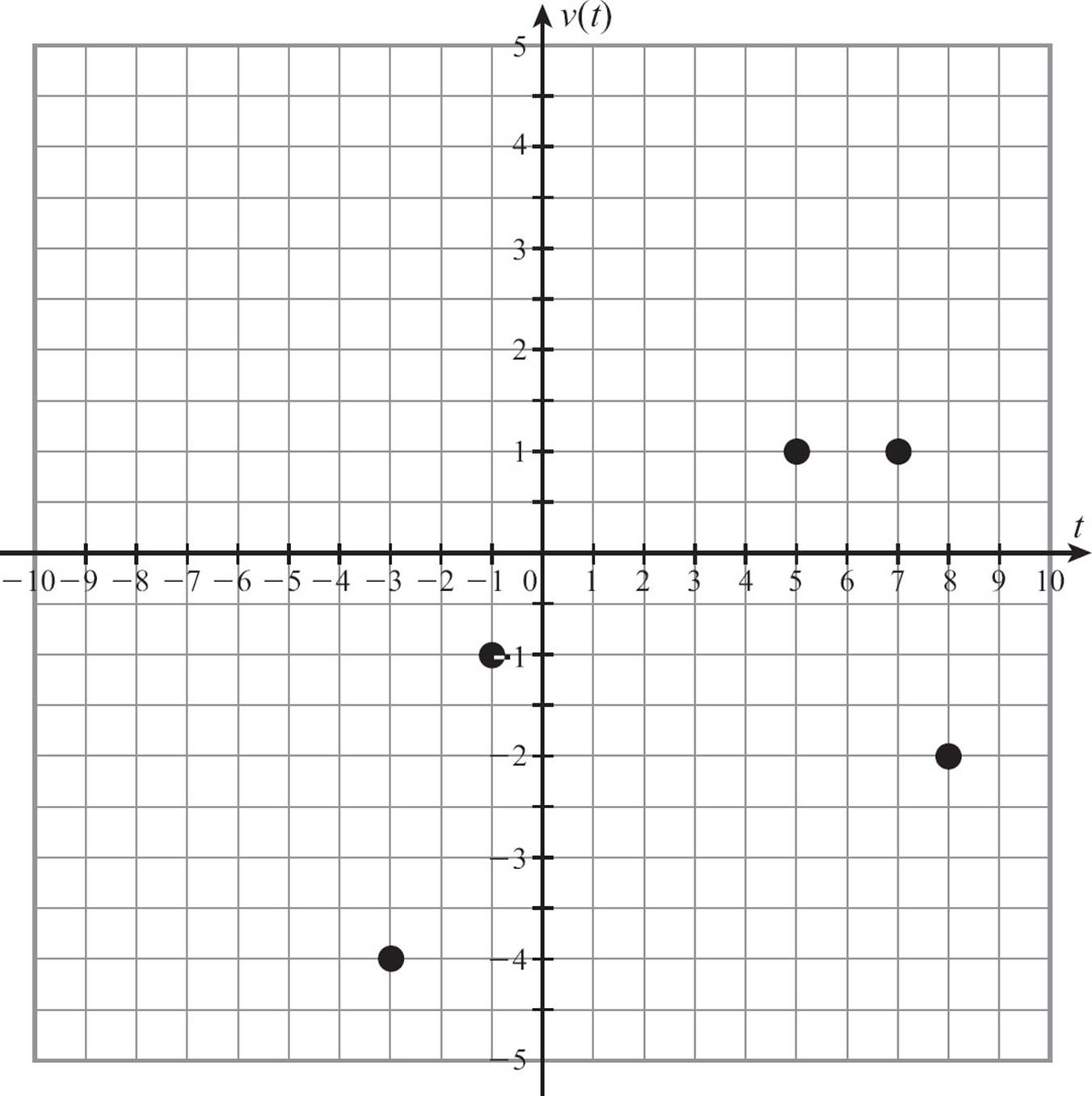
When there’s a clear pattern to the graph, it’s natural to want to connect the dots, to make a line or a curve that passes through all the pairs and highlights the pattern of the function. Sometimes it’s appropriate to do that, but other times it’s not.
Drawing that line says the function includes not only the pairs of numbers you plotted to see the pattern, but also all the pairs of numbers that name points on the line. That may or may not be true. If a function has a domain of all real numbers, and is defined by a rule, it’s common to evaluate the function for a few values and plot those points, until you can see the pattern, and then connect the dots. But not every function has the whole set of real numbers as its domain.
![]()
THINK ABOUT IT
Division by zero is impossible, so if a variable appears in a denominator, you need to figure out what values of the variable might make that denominator equal zero, and eliminate them from the domain. It’s also impossible to find the square root of a negative number in the real numbers, so if your function involves a square root, you need to eliminate any values of the variable that would give you a negative underneath the square root sign.
When you’re wondering whether to connect the dots or not, you should read the information you’re given carefully to see if you’re told what the domain is. If it’s all real numbers, you can feel free to connect. If the domain isn’t stated, and you’re given a table of values, assume that the function is just those pairs. Plot points, but don’t connect. If the domain isn’t stated, and you’re given a rule, you can assume the domain is all numbers that can sensibly be substituted for the variable. Generally, that will be all real numbers, unless there’s a variable in a denominator or under a square root sign.
![]()
CHECK POINT
Draw a graph of each function. Should the graph be separate points or a continuous line or curve?
31. 
32. f (x) = 2x − 3
33. g (x) = x2 − 5
34. v (t) = 10 − t2
35. a (t) = 5 − 3t
36. 
37. v (t) = −2t2
38. f (x) = 5 − 4x
39. 
40. g (x) = −2x
Vertical Line Test
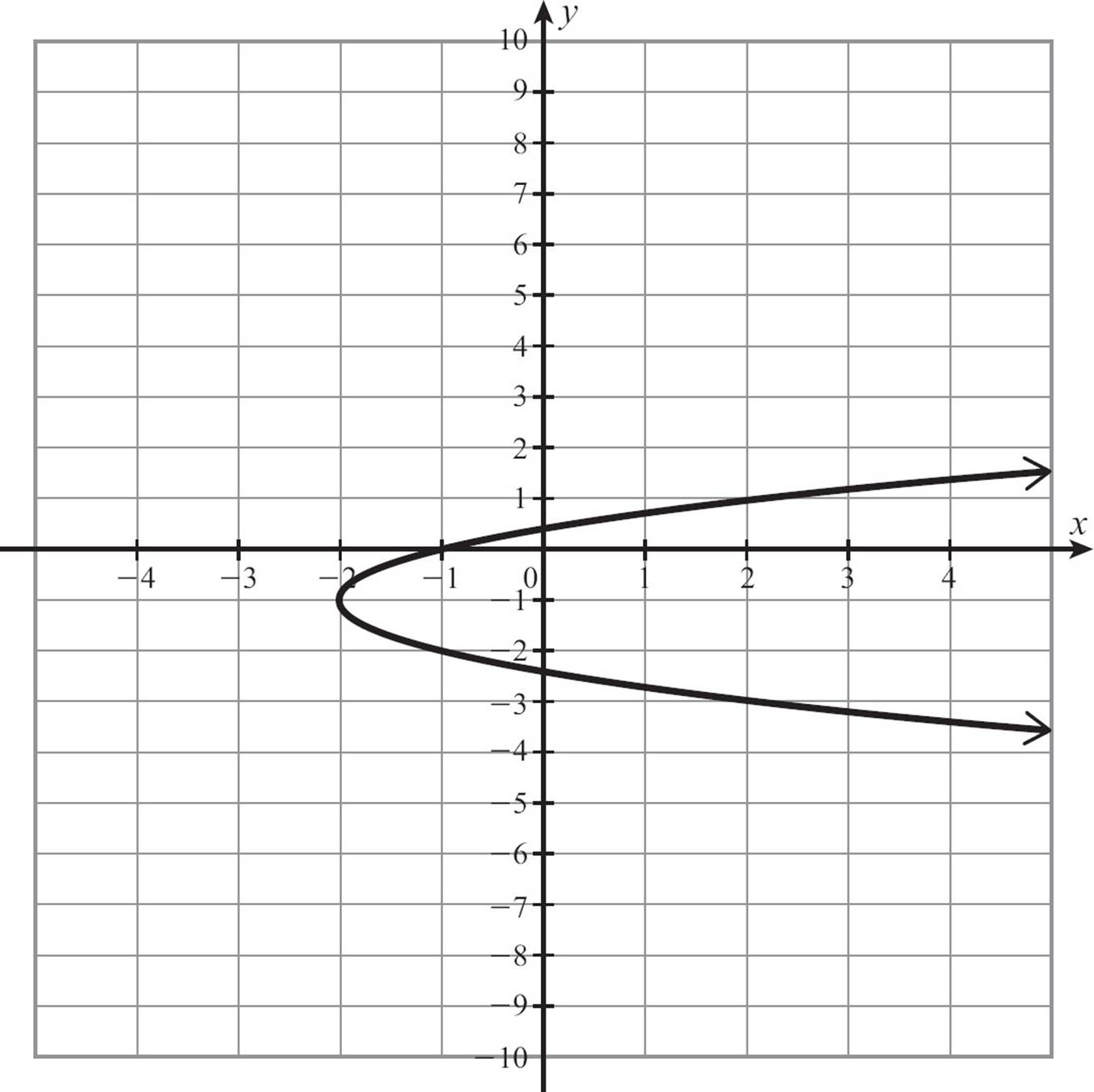
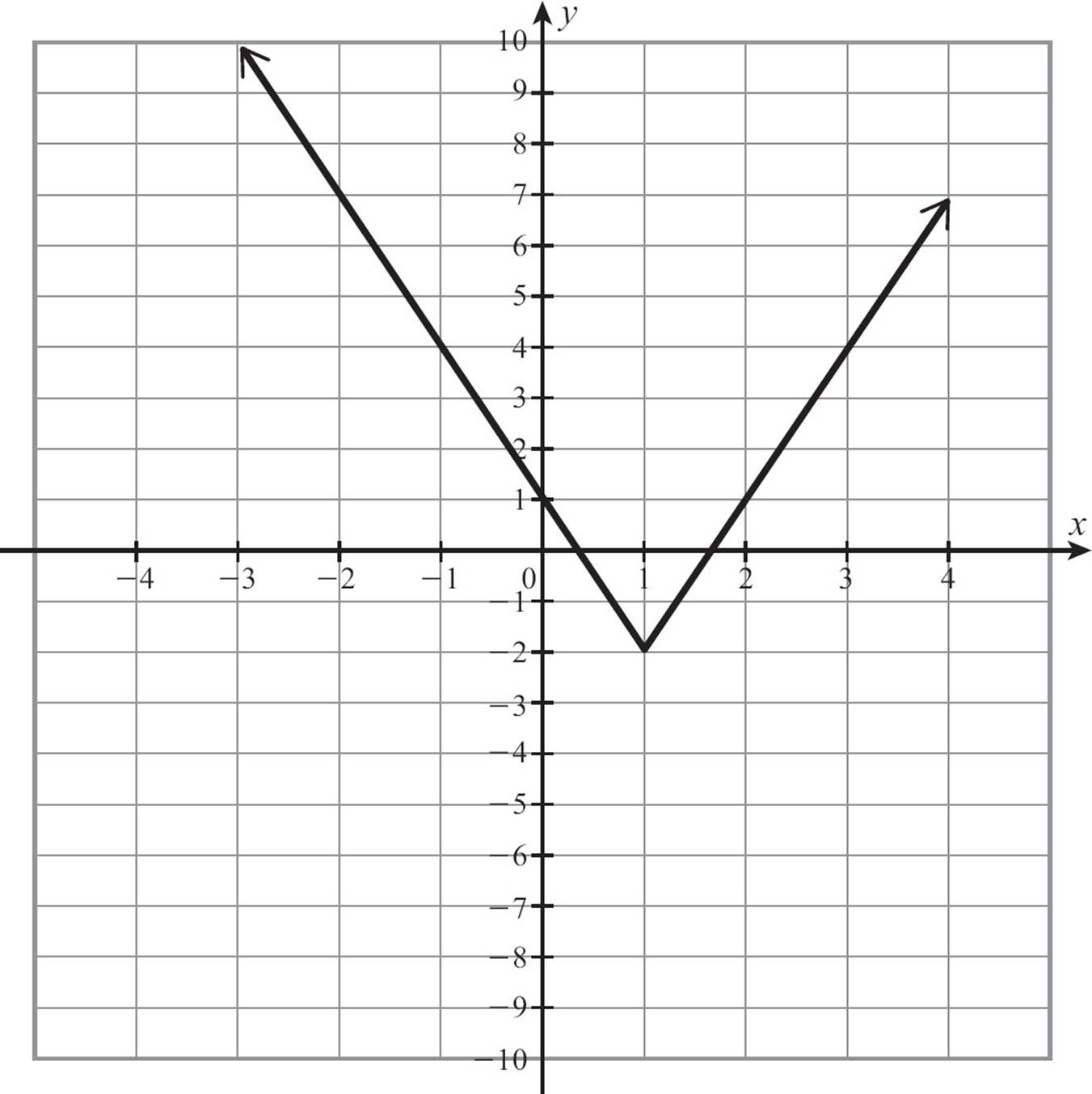
Presenting a relation as a graph also gives us a quick way to decide if the relation is a function, or more accurately to decide if it’s not a function. A relation is not a function if you can find any input that has more than one output. When you’re looking at a graph, that shows up as two (or more) points stacked vertically. The quick test is called the vertical line test.
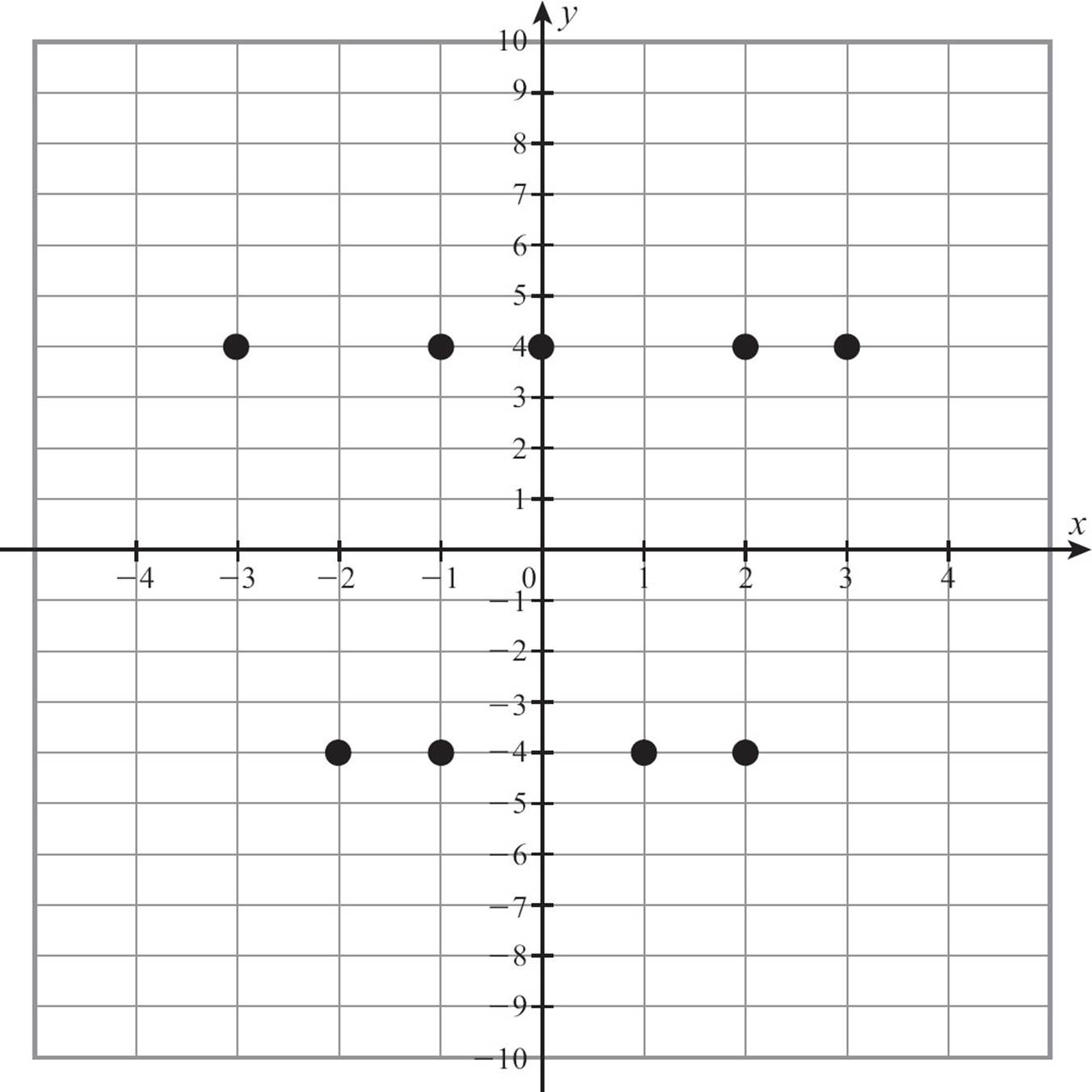
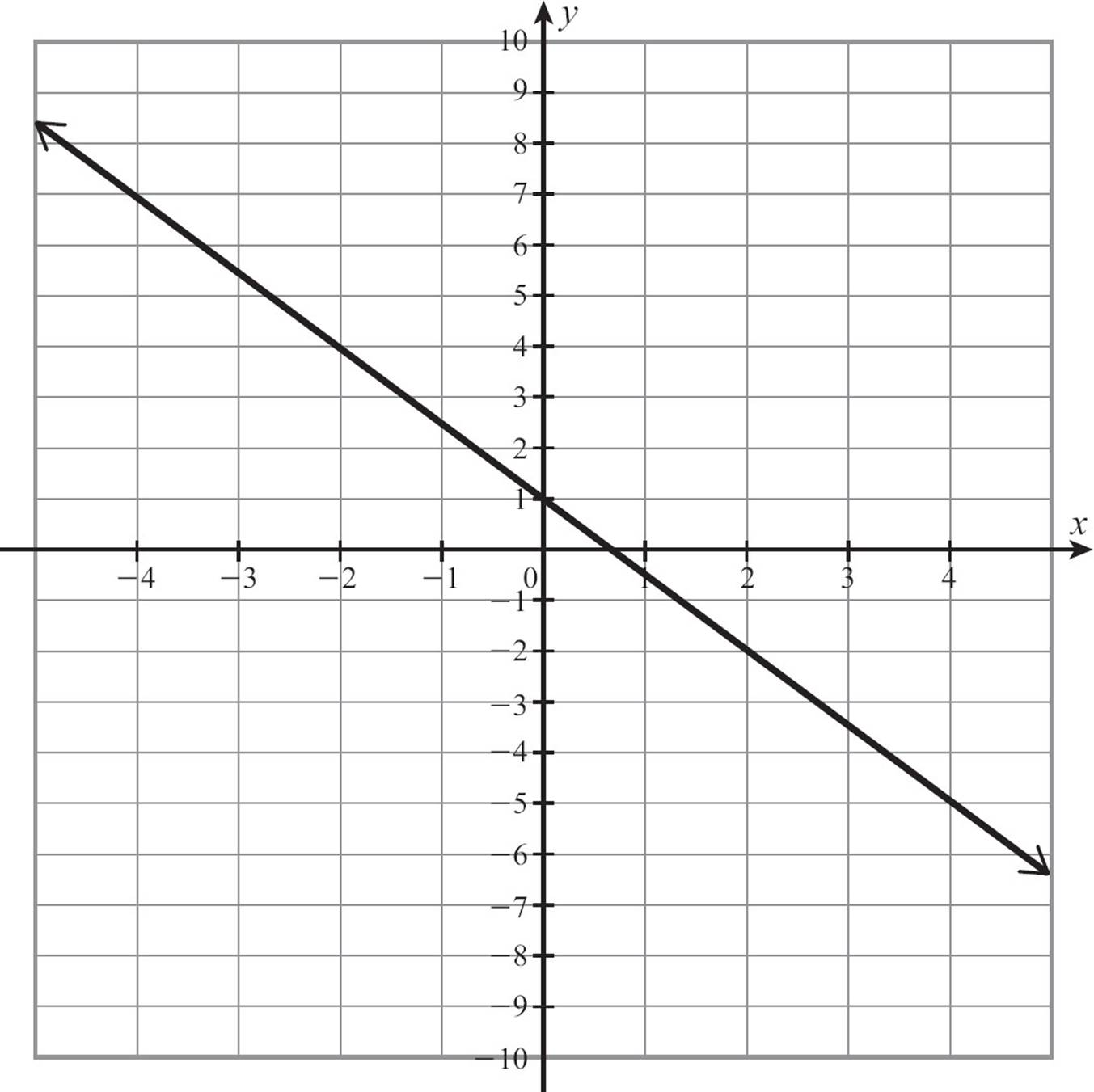
If any vertical line crosses two or more points of the graph of a relation, the relation is not a function. Some people call this the pencil test, because you can take your pencil, hold it vertically and move it across the graph. If it ever crosses two points, the graph does not represent a function. The graph on the left is not a function. You can see several places were points are stacked in a vertical line. The graph on the right is a function.
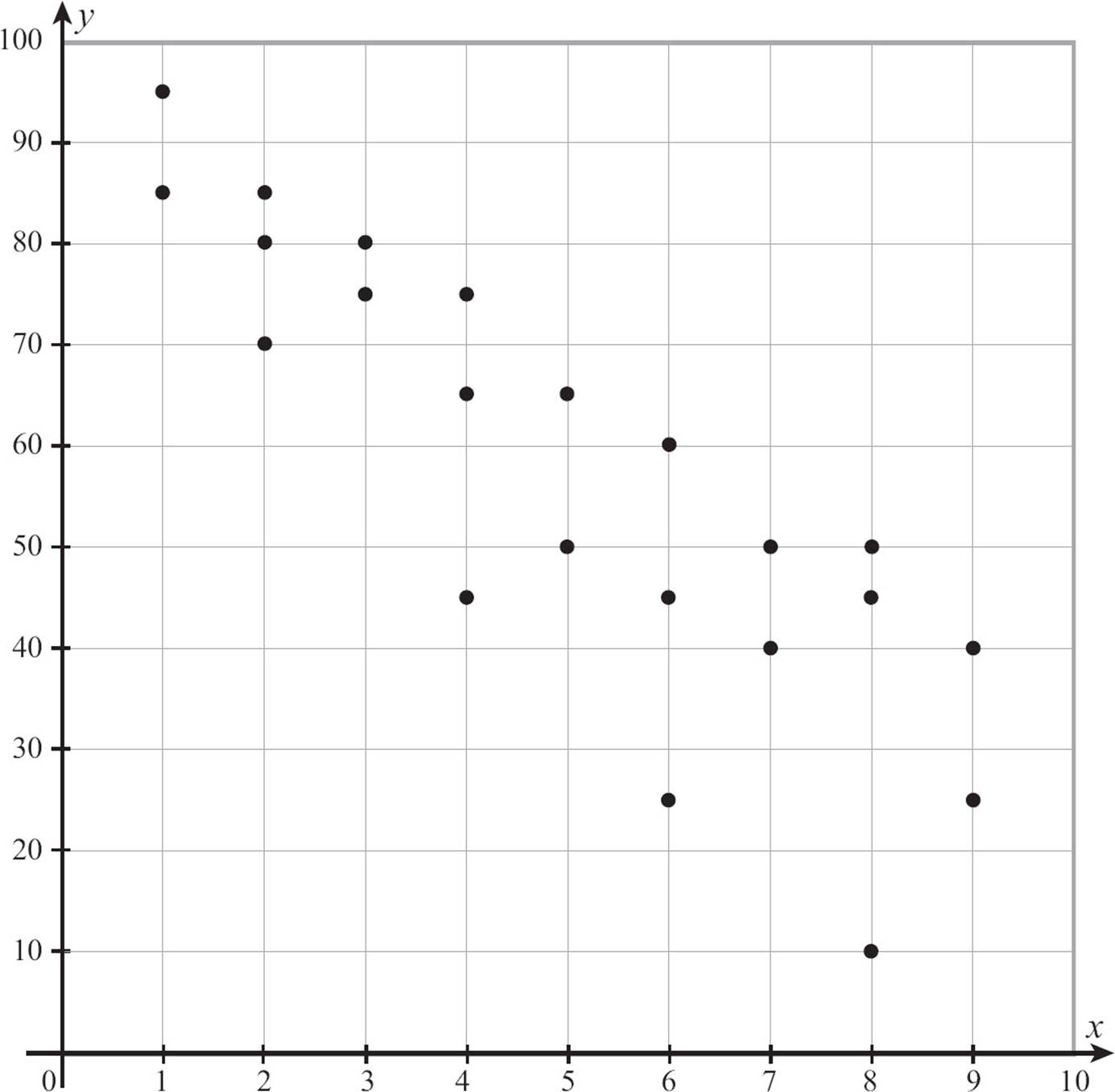
![]()
CHECK POINT
Use a vertical line test to determine whether each graph represents a function.
41. 
42. 
43. 
44. 
45. 
Construct a graph for each relationship below and use the vertical line test to determine if the relationship is a function.
46. 
47. 
48. y = 3x2 − 1
49. 2x + 3y = 12
50. 9x + y2 = 4
The Least You Need to Know
· A function is a pairing of numbers in which each input has only one output.
· The function notation f (x) tells you that you have a function, that its name is f, and that the variable x stands for its inputs.
· You can show a function by a list of pairs, a table of values, a graph, or a rule that tells you how to calculate outputs.
· A graph that shows a function will pass the vertical line test: no vertical line crosses it twice.
· f (3) means find the output of function f when the input is 3.