Idiot's Guides: Algebra I (2015)
Part II. Linear Relationships
Have you noticed that at the beginning of a detective story, the investigation seems to move along just fine? The detectives gather their evidence and seem to be on a straight simple path to closing the case. That won’t last, of course, but it always seems to start that way.
Algebra starts with a straight path, too. The beginning of algebra is a straight line study. We investigate functions whose graphs are lines, understand what makes an equation a linear function, and learn to solve linear equations and inequalities. That’s the plan for Part 2 of this book, so get in line, and let’s solve this case.
Chapter 4. Equations
In This Chapter
![]()
· Understanding equations
· Simplifying to make solving easier
· Solving one- and two-step equations
· Using equations to describe situations
A great writer can craft a beautiful phrase, a combination of words that is so true, so perfect, so pleasing, that it stops you in your tracks. But if all that author ever wrote were phrases, there wouldn’t be much of a story. No matter how beautiful the phrases are, eventually you have to put them together into sentences in order to communicate your thoughts.
Expressions, no matter how well they describe the mathematics you see happening, are just phrases. To truly communicate, you have to assemble expressions into mathematical sentences. In this chapter, we’ll look at the most common mathematical sentence, the equation, and see how we can use equations to help us find the value of the unknowns the variables represent.
The phrase “the product of –4 and a number x” becomes the expression −4x. The sentence “The product of –4 and a number x is –8” becomes the equation −4x = −8. The equal sign serves as the verb in the mathematical sentence. The expression is on the left side of the equation and the number –8 is on the right side.
![]()
TIP
The relationship of equality is symmetric, which means that if a = b, then b = a. What that means for you is that the equations −4x = −8 and −8 = −4x say exactly the same thing. Rewrite in whichever form you prefer.
Like expressions, equations vary from very simple to very complicated, but if you translate each phrase as you read it, you’ll get the right equation. The sentence “The product of 9 and a number x, decreased by 3, is 10 times the number” becomes 9x − 3 on the left side, the part before the “is” or equal sign, and 10x on the right. The equation is 9x − 3 = 10x. Translating “The difference of a and 3, multiplied by -5, is zero” requires parentheses. It becomes − 5(a − 3) = 0.
Simplifying Before Solving
When you approach an equation, you’re eager to get to the unknown, to find out what number that variable is standing for. But it wouldn’t make sense to try to get to the value of the variable without first stripping away some of the complications. In the case of equations, those complications take the form of expressions that can be simplified.
Before you begin to solve an equation, you want to simplify both sides of the equal sign as much as possible. Don’t even think of it as an equation yet. Just see it as two expressions, treat each side as a separate job, and do any simplifying you can. For equations without exponents or roots, your goal should be to have no more than two terms on either side: a variable term and a constant term.
The equation 2(x − 7) + 5 = 3x + 1 + 7x isn’t ready to solve. Focus on the left side, 2(x − 7) + 5. Distribute the 2, and 2(x − 7) + 5 becomes 2x − 14 + 5. Then combine the like terms -14 and +5, and the left side of the equation becomes 2x − 9. That’s two terms, one variable term, 2 x, and a constant term, -9, so that side is now simplified enough. Turn your attention to the right side, 3x + 1 + 7x. Combine the like terms, 3x and 7x, and the right side becomes 10x + 1. That’s two terms, a variable term and a constant term. The equation that started as 2(x − 7) + 5 = 3x + 1 + 7x has turned into 2x − 9 = 10x + 1. Each side has two terms, a variable term and a constant term. Now the equation is ready for solving. When you simplify, remember PEMDAS, the order of operations, and be sure to combine only like terms.
![]()
ALGEBRA TRAP
When you simplify, remember the order of operations. 6− 4(x + 1) is not 2(x + 1). The multiplication must be done before the subtraction. 6 − 4(x + 1) = 6 − 4x − 4 = 6 − 4 − 4x = 2 − 4x.
![]()
CHECK POINT
Simplify the expression on each side of the equation. Leave no more than two terms on any side.
1. x + (x + 1) + (x + 2) = 132
2. (2y − 5) + (y + 8) = 6 + (y − 3)
3. 4t − 2(t + 5) = 8 + t − 3
4. 2(x − 4) = 3x −(x + 1)
5. 16−(3a − 7) = (8a − 4) − 2(a + 5)
6. x + (x + 3) = 5(x + 2) − 7
7. 4(v − 3) = 6 − 2(v + 1)
8. 5(x − 3) − (x + 2) = (6x− 1) + 3(x + 8)
9. − 3(t + 5) + 9t = 5(t + 1) − (20 − t)
10. 4a − 7(a + 3) + 2 = 6 + 3(1 − a) − 5
Solving One-Step Equations
The most complicated equation you should try to solve is one that has a variable term and a constant term on each side. Anything more complicated than that should be simplified before you try to solve. Before you try to solve equations with two terms on each side, however, let’s start with a very simple equation that only takes one step to solve.
Every equation talks about what happened to an unknown number and what the result was. The equation 2y = 10 says an unknown number y was multiplied by 2 and the result was 10. Solving the equation means figuring out the value of the unknown number. What number, multiplied by 2, gives you 10?
For simple equations, your basic number sense or a bit of trial and error can usually answer that question, but it’s important to build a collection of skills that will get you to the answer when intuition isn’t enough. To solve the equation, you start with the result, 10, and undo the multiplication that was done to the unknown by performing the opposite or inverse operation. To find out what value of the variable y solves the equation 2y = 10, you can divide 10 by 2 to get back to y = 5. The variable was multiplied by 2 to get 10, so you divide 10 by 2 to get the value of the variable.
Multiplication and division are inverse operations. If the variable was multiplied by a number, you solve by dividing the result by that number. If the variable was divided by a number, multiply the result by that number. To solve 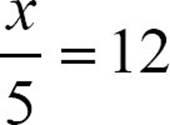 , multiply 12 by 5, to find that x = 60. Addition and subtraction are inverses. Solve the equation x + 7 = 22 by subtracting 7 from 22 to get 15. Solve t − 3 = 8 by adding 3 to 8, for a solution of 11.
, multiply 12 by 5, to find that x = 60. Addition and subtraction are inverses. Solve the equation x + 7 = 22 by subtracting 7 from 22 to get 15. Solve t − 3 = 8 by adding 3 to 8, for a solution of 11.
Now all that probably seems right. You can check that the answers are correct by asking “does 2 times 5 equal 10?” or “does 11 minus 3 equal 8?” But why does this “do the opposite” thinking work?
![]()
THINK ABOUT IT
Spending the time to understand why a particular process got you to the right answer guarantees that it wasn’t just a happy accident. If you can explain why it works, you can be confident it will work all the time.
An equation is like a balanced scale. The expressions on both sides of the equal sign have the same value. If you make a change on only one side, you’ll throw the scale out of balance. The expressions won’t be equal anymore. But if you make the exact same change to both sides, the scale will remain balanced.
When you solve x + 7 = 22, you don’t just subtract the 7 from the 22. You subtract 7 from both sides.
x + 7 = 22
x + 7 − 7 = 22 − 7
Doing the same thing on both sides keeps the scale balanced, and combining the like terms on each side gives you a simpler equation that tells you the value of the variable.
x + 7 = 22
x + 7 − 7 = 22 − 7
x = 15
Properties of the real numbers say that you can add the same number to both sides of an equation, subtract the same number from both sides, multiply or divide both sides by the same number, and the equation will stay balanced.
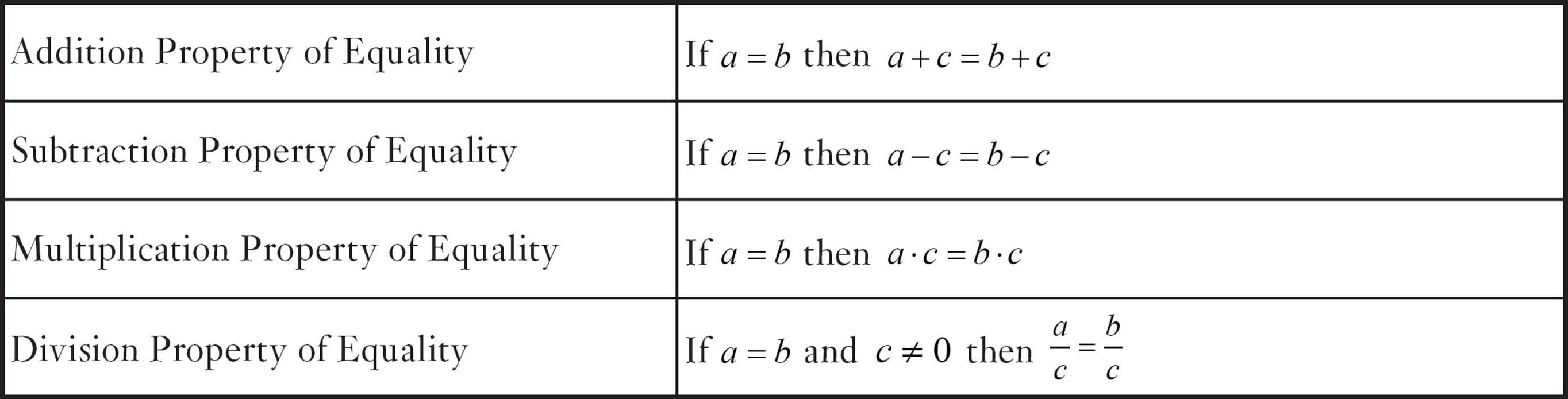
![]()
THINK ABOUT IT
The division property of equality has an extra bit that says the number you’re dividing by can’t be 0. Division by 0 is impossible. If you were asked to divide 12 by 3, you could think of it as breaking 12 into groups of 3, but if you try to divide 12 by 0, you can’t break 12 into groups of nothing. While multiplying by 0 is legal, it’s not useful either. It will give you 0 = 0, no matter what you started with.
When you solve 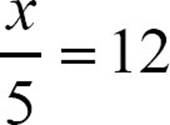 , this is what is really happening:
, this is what is really happening: 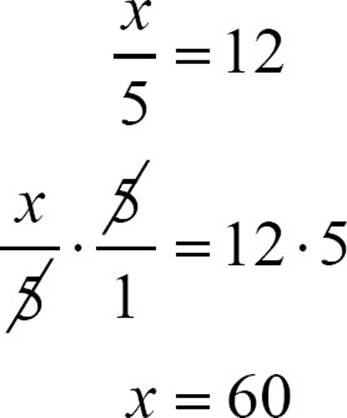
To solve an equation, perform the inverse operation on both sides. That reduces one side to just the variable and the other to original value of the variable. Remember your goal is to get the variable all alone on one side and a number all alone on the other side. Focus on eliminating anything on the variable side that isn’t the variable.
![]()
CHECK POINT
Solve each equation by performing the inverse operation.
11. 5x = 35
12. t − 3 = 17
13. y + 18 = 45
14. 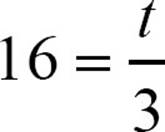
15. a + 39 = 14
16. w − 11 = 0
17. −8x = 72
18. t − 56 = 293
19. 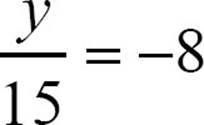
20. z + 91 = 91
Solving Two-Step Equations
To solve a one-step equation, you perform the opposite, or inverse, operation. Unfortunately, most equations you encounter involve more than one operation. The key will still be inverse operations, but which operation, and when?
To answer that question, you have to go back to the order of operations. An equation, like 3x − 5 = 16, says that a certain number, x, was multiplied by 3, and then 5 was subtracted from the result, and the final answer was 16. Starting with what the number x represents, the order of operations tells you to multiply first, and then subtract. We want to do the inverse, or opposite. We want to undo what was done.
![]()
THINK ABOUT IT
When you get dressed, you put on your socks, and then your shoes. When you undress, you take off your shoes before taking off your socks. Creating an expression is like getting the variable dressed. Solving an equation is undressing the variable. Inverse operations, opposite order.
Solving is going in the opposite direction, so you need to reverse the order of operations. The last thing that happened before arriving at the final answer of 16 was subtracting 5. Undo that part first by adding 5 to both sides of the equation.
3x − 5 = 16
3x − 5 + 5 = 16 + 5
3x = 21
Remember that an equation must be balanced. Each side of the equal sign must have the same value. In order to maintain that balance, you have to perform any operation you do to both sides.
Before that subtraction happened, but after the variable was multiplied by 3, you had 21. To get back to the original value of the variable, you need to undo that multiplication. You can do that by dividing both sides by 3.
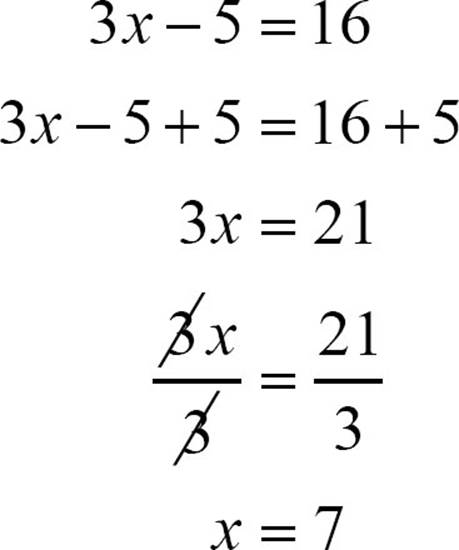
To solve a two-step equation, follow these steps.
1. Identify the two operations that have been performed on the variable, and the order in which they were performed.
2. Perform the inverse of the last operation, and simplify.
3. Perform the inverse of the remaining operation.
![]()
TIP
If you don’t like working with fractions, you can multiply both sides of the equation by the common denominator of the fractions. That will eliminate all the fractions. It may give you bigger numbers to work with, so choose wisely.
To solve −5x + 12 = 2, first note that x was multiplied by -5, and then 12 was added. Undo the addition first by subtracting 12 from both sides.
−5x + 12 = 2
−5x + 12 − 12 = 2 − 12
−5x = − 10
Undo the remaining multiplication by dividing both sides by -5.
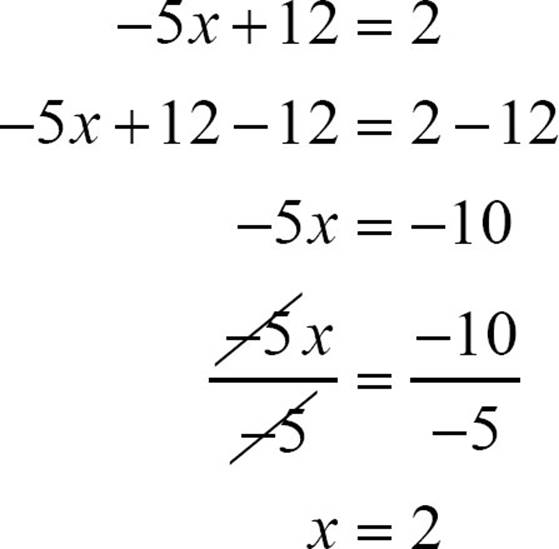
![]()
CHECK POINT
Solve each equation by performing inverse operations in reverse order.
21. 3a + 5 = 26
22. 2z − 7 = − 15
23. − 4n + 5 = 33
24. 11y − 9 = 2
25. 6t + 23 = − 7
26. 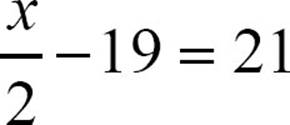
27. 3z − 2.5 = 5
28. − 19w − 72 = 4
29. 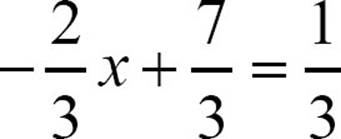
30. 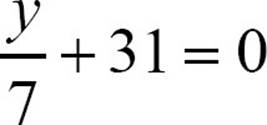
Equations with Variables on Both Sides
The simple skill you need to solve equations is do the opposite. Perform the inverse operation. If it’s a two-step equation, perform the inverse operations in reverse order. The key to making those simple rules work for you is simplifying each side of the equation before you start solving. You never want to start solving until you have simplified enough that there are no more than two terms on either side.
Thus far, the equations we’ve solved all had one side with only one term. What if there are two terms on both sides? Or if the side that has only one term has a variable term, not a constant? Your strategy is still focused on inverse operations with just a small adjustment.
If the equation has variable terms on both sides, eliminate one by adding or subtracting. If you need to solve 7a − 3 = 5a + 9, your first move is to eliminate one of the variable terms. You can choose either one to eliminate. Usually, we eliminate the smaller one, but it’s entirely up to you. Let’s eliminate the 5a by subtracting 5a from both sides.
7a − 3 = 5a + 9
7a − 3 − 5a = 5a + 9 − 5a
2a − 3 = 9
Once you’ve eliminated one of the variable terms, and there’s only a constant on one side, then you can follow the plan for a two-step equation. Add 3 to both sides, then divide both sides by 2.
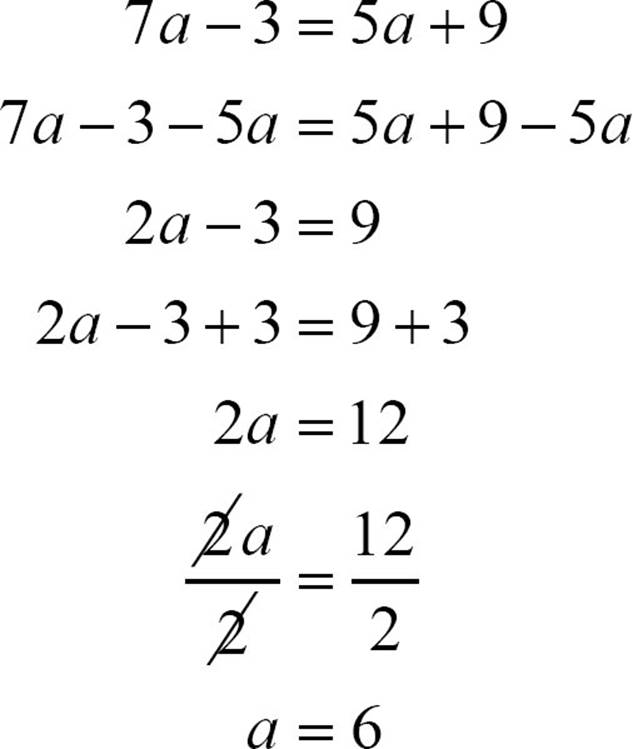
If you find yourself with an equation that has two terms on one side and one term on the other, but it’s a variable term, you can still choose to eliminate either variable term, but you’ll do less work if you eliminate the variable term on the two-term side. Suppose you need to solve 8x − 9 = 5x. You can eliminate the 5x or the 8x. If you choose to eliminate the 5x, it looks like this.
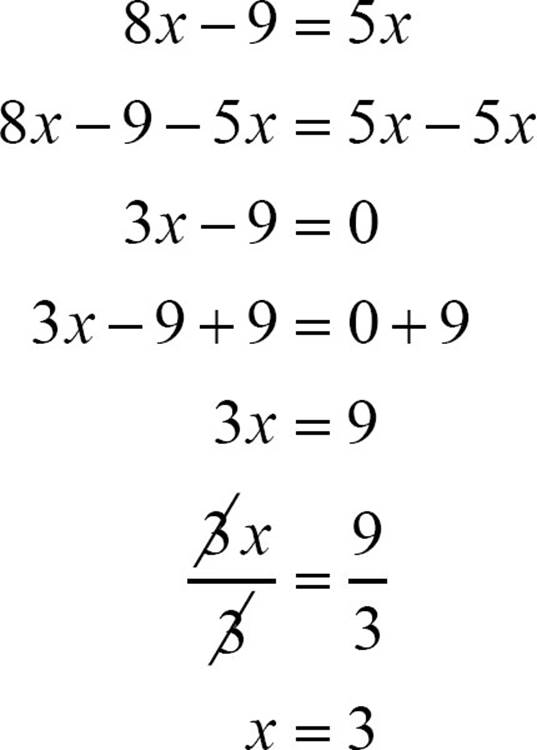
If you choose to eliminate the 8x, it’s a little shorter.
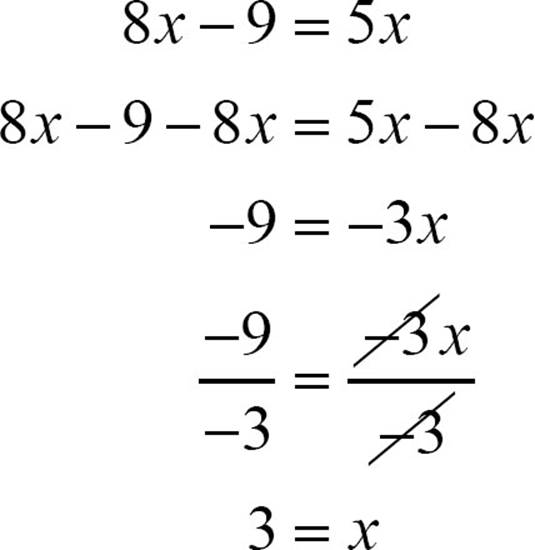
![]()
TIP
There is often more than one correct way to solve an equation. You could, for example, solve without simplifying first. It’s not “wrong.” It just takes longer and has more opportunities to make mistakes. Have a plan, a habit, of how you do things, and you’ll find your work is more accurate.
Some equations, like x = x + 1, have no solution. Sometimes you can see just by reading the equation that it makes no sense. A number can’t equal more than itself. When you try to solve, all the variables disappear and what’s left is a false statement.
x = x + 1
x −x = x + 1 − x
0 = 1
Zero clearly doesn’t equal 1. The equation has no solution.
There are also equations for which all the variables disappear, but the resulting statement is true. When you try to solve 5x − 7 = 3(x − 2) + 2x − 1, you find it simplifies to
5x − 7 = 3(x − 2) + 2x − 1
5x − 7 = 3x − 6 + 2x − 1
5x − 7 = 5x − 7
The fact that both sides are exactly the same tells you that any number could replace x and the equation would still balance. But if you didn’t realize that and went on to solve, look at what will happen.
5x − 7 = 3(x − 2) + 2x − 1
5x − 7 = 3x − 6 + 2x − 1
5x − 7 = 5x − 7
5x − 7 − 5x = 5x − 7 − 5x
− 7 = − 7
All the variables have disappeared and the remaining statement is true. That’s a sign that any real number will solve this equation. Equations that are true for any value of the variable are called identities.
![]()
TIP
You can always check a solution by plugging the value you found back into the equation and simplifying both sides. If both sides come out the same, your solution is correct. If not, first double-check your work in the check, and if that’s accurate, double-check your solution.
![]()
CHECK POINT
Solve each equation by performing inverse operations in reverse order.
31. 3x − 7 = 5x + 1
32. 2t + 5 = 3t − 2
33. 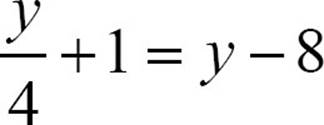
34. 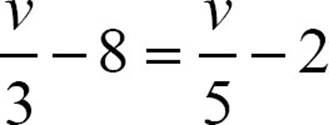
35. 11 + 8x = 12x − 17
36. −2(y − 7) = 4y − 6(y + 1)
37. 8(x + 5) = 2(x − 3) + 7(x − 1)
38. 2t− 3(t + 1) = (2− 1)− 5
39. (4z− 5) + (2z + 7) = (3z− 4) + 2(z + 3)
40. x − 13 = 5(x + 10) − 17
You now have all the skills needed to solve first degree, or linear, equations in one variable. All equations with a single variable, with no exponents or roots, and no variables in denominators, can be solved by simplifying each side of the equation, and then using inverse operations. Those are powerful tools, but only if you know when and how to use them.
If someone asks you to build a model of the Eiffel Tower or the Empire State Building, you understand that they want you to construct a smaller, simpler version of the landmark. When someone asks you to do some mathematical modeling, they’re suggesting that you use your math skills to write a clear compact mathematical sentence that describes what’s going on in a particular situation.
Modeling with Linear Equations
Modeling is finding a way to represent a situation using math. Right now, we’ll do that using algebra, specifically, linear equations. Sometimes the situation you’re trying to represent is described in language that translates directly into algebraic representations.
Find two numbers such that one number is 12 more than another and their sum is 42. You can represent one number with a variable, say x, and the other as x + 12. The word sum means addition, so x + x + 12 = 42. Combine like terms on the left side of the equation, and 2x + 12 = 42. Then solve the equation.
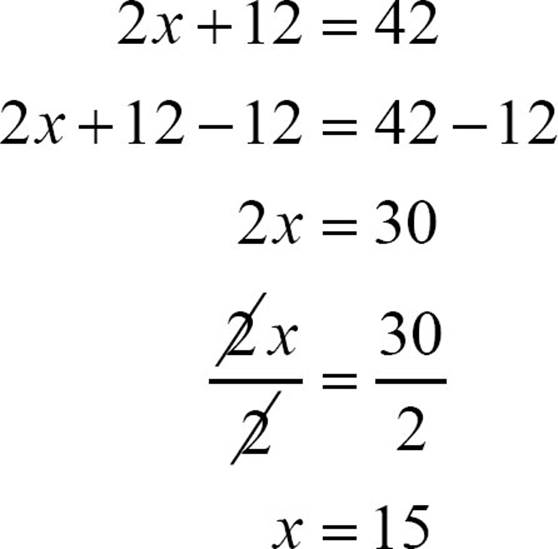
Don’t move on just yet, because you still need to put this solution in context. You were looking for two numbers, and you called one of them x. That number is actually 15. The other number is 12 more than that, so it must be 15 + 12, or 27. The two numbers are 15 and 27, and if you check, they do add to 42.
Much of the time, however, the situation you have to represent isn’t presented in a way that translates quite so easily to equations. George has a budget of $40 for school supplies. He has already spent $10.05 on folders and pens, but still needs to buy notebooks. The type of notebook he prefers sells for $5.99. How many notebooks can George purchase?
There are a lot of distractions from the simple this number plus that number equals the other number language of the previous example. It may help to begin by trying to state the situation in simpler terms. You might state this one as what George spends on folders and pens plus what he spends on notebooks equals $40, or in even simpler terms, folders plus notebooks equals $40.
![]()
TIP
Take the time to define your variable. It helps you understand what the question is asking, it helps your reader understand the solution you’re presenting, and it helps you reflect afterward on whether your answer makes sense. If n is the number of notebooks and you get n = −32.4, you know something went wrong.
Focus in on what you need to find out and define a variable. You need to find out how many notebooks George can buy, so let n = the number of notebooks. If George buys n notebooks, how much does he spend on notebooks? Each notebook costs $5.99, so he’ll spend 5.99n on notebooks, and he’s already spent $10.05 on folders and pens.
Organize the information.
Let n = the number of notebooks George can buy
Let 5.99n = the amount George spends on notebooks
Let 10.05 = the amount George spends on folders and pens
Let 40 = George’s budget
State the situation simply.
(amount for notebooks) + (amount for folders and pens) = 40.
Insert the symbols.
5.99n + 10.05 = 40
Now you have an equation you can solve.
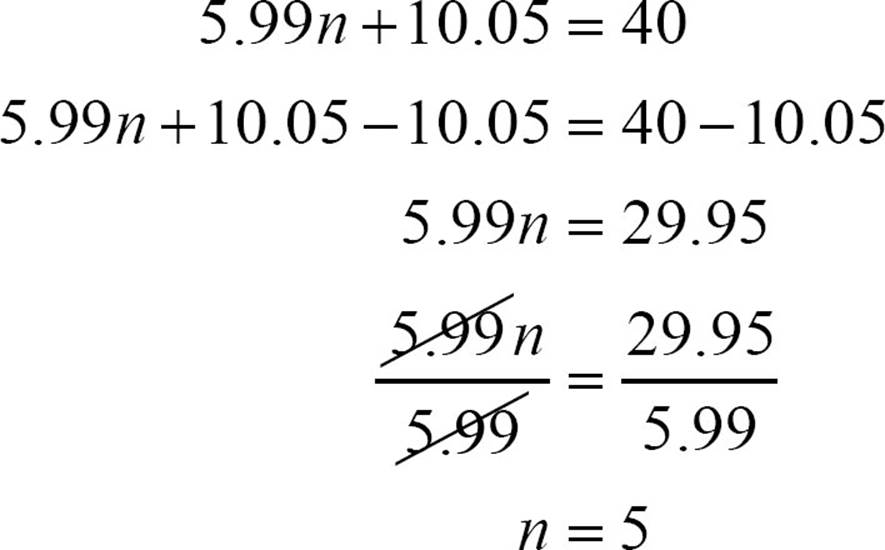
George can buy five notebooks. (Of course, even this isn’t a “real life” situation. In real life, there’d be tax to consider, and the solution probably wouldn’t be a tidy integer answer.)
When you’re trying to model a situation with an equation:
· Read the problem carefully.
· State the situation in the simplest possible language.
· Identify what you need to find.
· Define a variable, and any variable terms that represent elements of the situation.
· Translate the simple statement of the situation into an equation.
· Solve the equation.
· Interpret the solution in the context of the situation, and make sure it makes sense.
![]()
CHECK POINT
For each problem, define a variable, write an equation that describes the situation, and solve the equation.
41. Six more than three times a number is twenty-seven. Find the number.
42. Twice a number increased by 4 is 8 more than the number. Find the number.
43. The sum of two consecutive numbers is 53. Find the numbers.
44. The cost of manufacturing storage containers is $100 plus $0.18 per container. If the total cost of an order was $1,000, how many storage containers were manufactured?
45. Francesca built a garden 3 feet longer than it is wide. She needed 30 feet of fencing to enclose the garden. Find the dimensions of the garden.
46. Christopher bought 3 hot dogs and spent $1.50 for a drink. His total bill was $12. Find the price of a hot dog.
47. Carlos saves $12 each week. Dahlia has already saved $270 and each week she spends $15 of that savings. When will they both have the same amount in savings?
48. Alyssa received a $100 gift certificate for her birthday and used it to order 12 e-books. Afterward there was $5.32 left on the gift certificate. What was the average price per e-book?
49. When her community organized a fundraiser, Sophie was asked to contribute packages of snacks that could be sold at the event. She decided to package her secret spiced almonds for sale. She bought almonds for $9 per pound, and spent $2 for spices. The total bill was $56. How many pounds of almonds did she buy?
50. Six times the difference of 12 and a number exceeds the sum of 12 and the number by 4. Find the number.
The Least You Need to Know
· Equations are sentences that say two expressions have the same value.
· Always simplify each side of an equation before trying to solve.
· To solve equations, perform the inverse operations in the opposite order.
· If there are variable terms on both sides of the equation, eliminate one by adding or subtracting.
· Some equations have no solution, and some are true for all values of the variable.