Idiot's Guides: Algebra I (2015)
Part II. Linear Relationships
Chapter 7. The Equation of a Line
In This Chapter
![]()
· Converting from one form of a linear equation to another
· Understanding the advantages of each form
· Finding the equation of a line
· Finding the equation of a line parallel to or perpendicular to a given line
Linear equations and functions are an important part of algebra. Not only do linear functions model many different situations on their own, but we often deal with other types of functions by translating them into linear functions. It makes sense to know how to solve linear equations and graph linear functions. Sometimes, however, we find ourselves needing to work in a different direction.
Many times we have information from which we can construct a graph, and when the graph is done, we realize we’re looking at a linear relationship. What we need to figure out is the equation that describes that linear function. In this chapter, we’ll look at the different forms in which a linear equation can appear, and how we take the information we have and work our way to the equation of the linear relationship.
Forms of the Linear Equation
When you first looked at linear equations and functions, you learned that a linear function has a simple variable term and a constant term. Of course, things aren’t always that simple and straightforward. When written in function form, using f (x) notation, linear functions usually appear just that way, f (x) = mx + b. When you use y or another variable to describe the relationship, things can get rearranged and look a bit different. Sometimes that’s useful, but other times you just want to get back to that y = mx + b form.
![]()
THINK ABOUT IT
What’s the difference between a linear equation and a linear function? Linear equations, like 3x – 12 = 9, have one variable, with no exponents, and need to be solved by finding the value of the variable. Linear functions connect two variables, usually xand y, by showing how they’re related or defining one in terms of the other, like y = 2x – 7. The functions are the ones you’ll graph.
You can always check whether an equation is linear by checking on what’s not there. Linear equations won’t have exponents, and won’t have variables under radicals or in denominators. But you also want to get to know the three different forms in which we see linear functions presented.
Slope-Intercept Form
Slope-intercept form, commonly referred to as y = mx + b form, should be familiar to you now. The form takes its name from the fact that it lets you see at a glance the slope of the line, m, and its y-intercept, b. This makes it a favorite form for graphing. If you have to graph y = 2x − 7, you know immediately that the y-intercept is (0, -7) and the slope is ![]() . With that information, you can quickly sketch the graph.
. With that information, you can quickly sketch the graph.
![]()
DEFINITION
Slope-intercept form defines the output variable, y, in terms of a multiple of the input variable, x, and a constant, b. y = mx + b
If you’re facing an equation that isn’t in slope-intercept form, you can rearrange it by the same kind of algebraic operations that you use to solve an equation. In this case, you want to solve for y, or isolate y. The equation 5y − 3x − 3 = −9 is not in slope-intercept form, but if we can get the y all alone on one side, we can get it to slope-intercept form. To do that, follow these steps.
1. Move any term that does not contain a y to the side opposite the y term by adding or subtracting. You can do this in one step or several. Expect to end up with the y term on one side, and up to two terms, an x term and possibly a constant term, on the other.
5y + 3x − 3 = 9
5y + 3x − 3 + 3 = 9 + 3
5y + 3x = 12
5y + 3x − 3x = 12 − 3x
5y = 12 − 3x
2. Rearrange the x-term and constant term, if necessary. The commutative property lets you do this. Remember you can think of subtraction as adding a negative.
5y = 12 − 3x
5y = 12 + − 3x
5y = −3x + 12
3. Divide both sides by the coefficient of y.
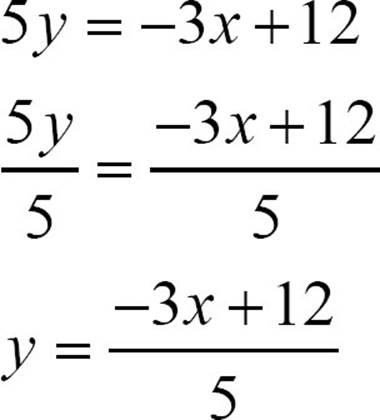
4. Simplify by dividing each term by the divisor. If the results of the division are not integers, fractions are more useful than decimals for slopes.
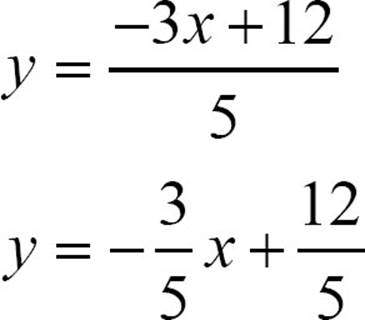
![]()
CHECK POINT
Put each equation in slope-intercept form.
1. 3x + 2y = 6
2. 6y − 3 = 12x
3. x + 5y = 10
4. 3x − y = 9
5. 4 − 2y = 8x
6. 4x − 8y = 16
7. 2y + 12x − 6 = 0
8. 
9. 4.5x + 3.5y + 31.5 = 0
10. 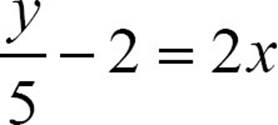
Standard Form
Another form in which you often see linear equations is called standard form. Standard form has an x term and a y term on the same side, and a constant on the other. This is the form you’d produce if you wanted to say that 4 hot dogs and 2 sodas cost $9. You’d write 4x + 2 y = 9. The x term and y term describing what you bought are added on the left side and the total cost is on the right side.
![]()
DEFINITION
Standard form is a way of writing an equation in which all the variable terms are on the same side, all the coefficients are integers, and the first coefficient is positive. ax + by = c
To put an equation in standard form, the basic step is to use addition or subtraction to move the variable terms to one side and the constant term to the other. There is more to the definition of standard form, however, that may add a step or two. Let’s look at the equation 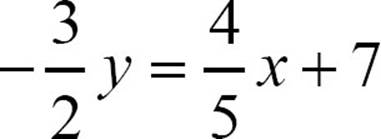 and put it in standard form.
and put it in standard form.
1. Get the variables on one side and the constant on the other by moving the x term to the side with the y term.
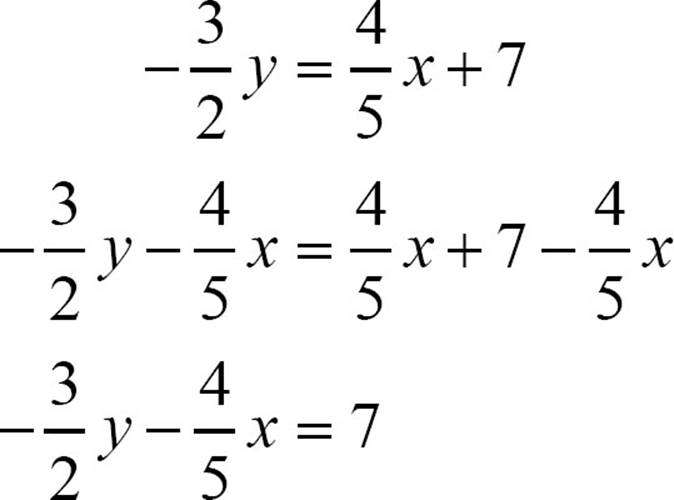
2. Rearrange the left side so the x term comes first.
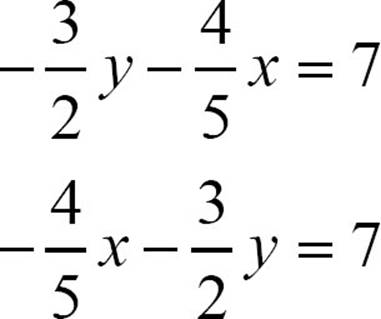
3. Change the coefficients to integers by multiplying both sides of the equation by the common denominator of all the fractions. In this case that’s 5·2 = 10.
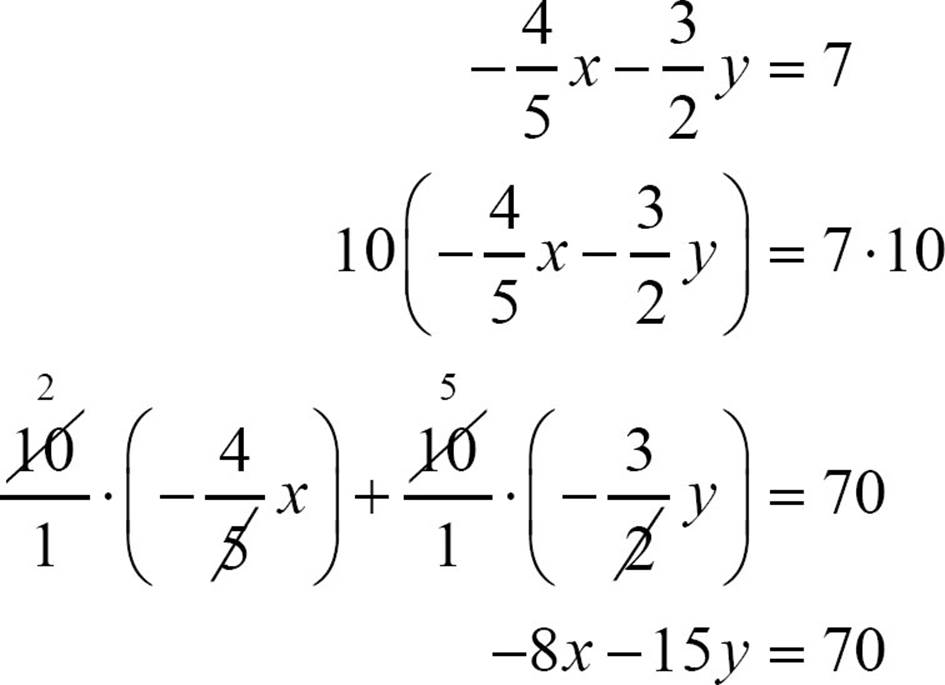
4. Make the first coefficient positive by multiplying both sides by -1.
−8x − 15y = 70
− 1(−8x − 15y) = 70·(−1)
−1(−8x) + (−1)(− 15y) = − 70
8x + 15y = − 70
Standard form, in addition to being tidy-looking, is a great form for graphing by intercept-intercept. If y = 0, solving 8x = −70 will give you the x-intercept, and if x = 0, solving 15y = −70 will give you the y-intercept.
![]()
CHECK POINT
Put each equation in standard form.
11. y = 6x − 7
12. y − 7 = 3(x + 2)
13. y = −3x + 5
14. y + 1 = −4(x − 3)
15. 4y = 8x − 32
16. 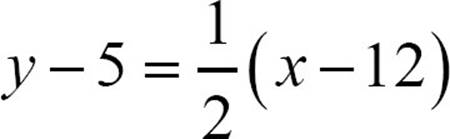
17. 5y = 3 − 4x
18. 2 y + 7 = −6 (x + 2)
19. 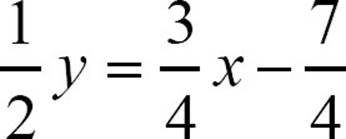
20. 5(y − 2) = −3(x − 6)
Point-Slope Form
The point-slope form is a powerful tool when you want to find the equation of a line, but you will rarely be asked to put an equation into this form. If a line has a slope, m, and passes through the point (x1, y1), the point-slope form of the line is y − y1 = m(x − x1). The equation of a line with a slope of -4 through the point (5, 2) is y − 2 = −4(x − 5).
![]()
DEFINITION
Point-slope form, y − y1 = m(x − x1), is a version of the linear function that defines the relationship between the variables x and y in terms of the slope of the line, m, and one point known to be on the line, (x1,y1). If a line with a slope of -3 passes through the point (4, -7), the equation of that line can be written as y − (−7) = − 3(x − 4).
![]()
CHECK POINT
Identify each equation as slope-intercept form, standard form, or point-slope form.
21. y − 7 = − 2 (x + 5)
22. 3x − 4y = 12
23. y = 2x − 6
24. x + y = 10
25. 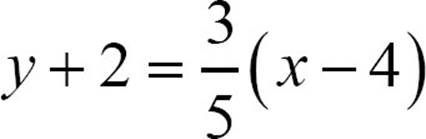
The slope-intercept form of a linear equation is perfect for graphing by slope and y-intercept. The standard form is useful for graphing by intercepts. The third form, point-slope form, could be used for graphing, but its real power is that it allows you to build the equation of a line from just a little bit of information about its graph.
Finding the Equation
There’s more than one way to find the equation of a line. The method you choose depends on what information you have. We’ll look at each possible situation.
Given the Slope and y-Intercept
If you know that a line has a slope of -3 and its y-intercept is (0, 7), you have very little work to do to find the equation of the line. Just use slope-intercept form, replace m with the slope and b with the y-intercept. y = mx + bbecomes y = − 3x + 7, and you are done.
![]()
CHECK POINT
Write the equation of the line with the given slope and y-intercept.
26. slope: -3, y-intercept: 0
27. slope: 5, y-intercept: -9
28. slope: ![]() , y-intercept: 5
, y-intercept: 5
29. slope: 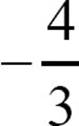 , y-intercept: -6
, y-intercept: -6
30. slope: 1, y-intercept: 3
Given the Slope and a Point
If you know the slope of the line and a point on the line, but that point is not the y-intercept, you’ll want to use point-slope form. This is exactly the situation for which the form is named. If you know that the slope of a line is ![]() and it passes through the point (3, 5), you can start with the point-slope form y − y1 = m(x − x1) and replace the appropriate pieces with numbers you know. The slope of
and it passes through the point (3, 5), you can start with the point-slope form y − y1 = m(x − x1) and replace the appropriate pieces with numbers you know. The slope of ![]() goes in place of the m, 3 in place of x1, and 5 in place of y1, and the form becomes
goes in place of the m, 3 in place of x1, and 5 in place of y1, and the form becomes 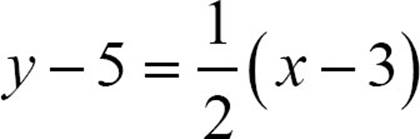 .
.
Technically, you’ve found the equation of the line at that point, but as mentioned earlier, point-slope isn’t really a form you work with. So let’s continue on to put this equation into slope-intercept form. (You could do standard form if you prefer.) Start by distributing the ![]() .
.
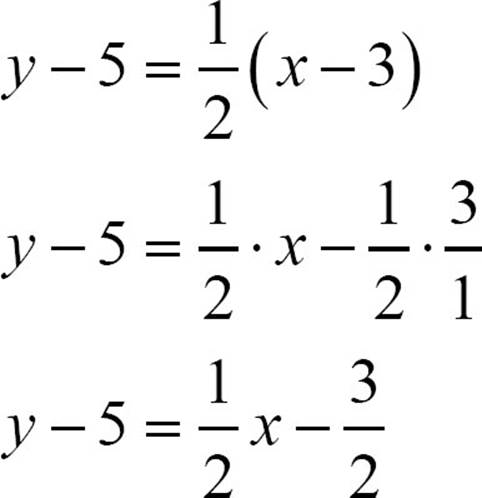
Then add 5 to both sides to isolate the y.
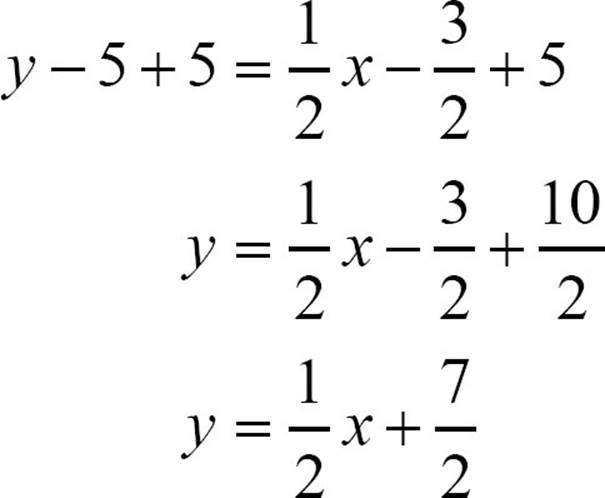
You might wonder why point-slope form is needed. If you can look at the graph to see the slope and a point, why not just look to see what the y-intercept is? The previous equation tells you what the problem might be. There’s no guarantee that the y-intercept will be an integer and if it’s not, estimating the fraction can be difficult. Point-slope form lets you use any convenient point.
![]()
CHECK POINT
Find the equation of the line with the given slope, passing through the given point. Put the equation in slope-intercept form.
31. Slope: -4, point: (-1, 7)
32. Slope: 5, point: (-2, 6)
33. Slope: ![]() , point: (9, 9)
, point: (9, 9)
34. Slope: 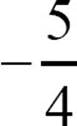 , point: (-8, 5)
, point: (-8, 5)
35. Slope: -1, point: (9, -4)
36. Slope: 2, point: (5, 7)
37. Slope: ![]() , point: (-8, 3)
, point: (-8, 3)
38. Slope: 1, point: (-4, -3)
39. Slope: ![]() , point: (-5, 1)
, point: (-5, 1)
40. Slope: 3, point: (6, -5)
If you know the slope and the y-intercept, use slope-intercept form. If you know a point and the slope, use point-slope form, and simplify. That seems fairly straightforward. But the information you have to work with isn’t always as tidy as that.
Suppose you have reason to believe that there is a linear relationship between an adult’s height and weight. You think that weight is a linear function of height, but you don’t have a rule for that relationship, and no one has conveniently told you the slope of the line. All you know is this particular adult weighed 120 pounds when she was 64 inches tall and 135 pounds when she was 67 inches tall. You have two points: (64, 120) and (67, 135). How do you find the equation of the line?
Given Two Points
If you know two points on a line, you have part of the information you need. You have a point; in fact, you have two. What you need is the slope. You could plot the two points you have on a graph, draw the line, and try to count the boxes to find the rise and run. Sometimes that’s a very efficient method, but in a case like this example, when the numbers are large, or if there are lots of fractions or decimals, it could be difficult.
![]()
TIP
The slope formula is usually given as 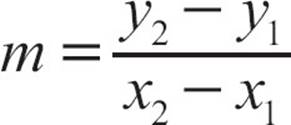 but if it’s more convenient, you can use
but if it’s more convenient, you can use 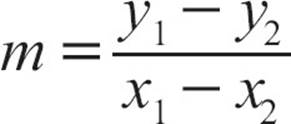 . It’s not important which point goes first, but it is important that you be consistent.
. It’s not important which point goes first, but it is important that you be consistent.
To find the slope of the line efficiently, you can calculate it using a formula. The slope of a line through the points (x1, y1) and (x2, y2) is 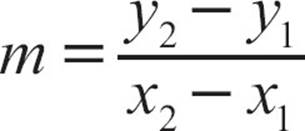 . The rise of the line can be found by subtracting the y-coordinates and the run by subtracting the x-coordinates. Then the slope is
. The rise of the line can be found by subtracting the y-coordinates and the run by subtracting the x-coordinates. Then the slope is 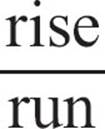 .
.
![]()
ALGEBRA TRAP
Be careful to keep the same order of subtraction in both the numerator and denominator. It doesn’t matter which point you call (x1, y1) and which you call (x2, y2), but if you switch the order from the numerator to the denominator, the sign of your slope will be wrong.
In the example, the points are (64, 120) and (67, 135). To find the slope of the line, you can use the formula 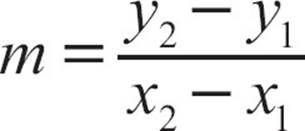 with (x1, y1) equal to (64, 120) and (x2, y2) equal to (67, 135). So the slope is
with (x1, y1) equal to (64, 120) and (x2, y2) equal to (67, 135). So the slope is
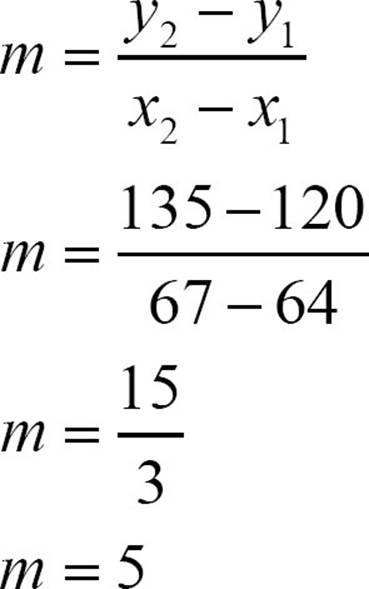
That’s saying each time the height increases by 1 inch, the weight increases 5 pounds.
Now you have a slope, m = 5, and your choice of either one of your two points, (64, 120) or (67, 135), which means you have enough information to use point-slope form to find the equation of the line. Start with the point-slope form, y − y1 = m(x − x1), and substitute 5 for the slope. y − y1 = 5(x − x1). Then choose one of the points—either one, but only one. Let’s use (64, 120). The 64 goes in place of x1 and the 120 goes in place of y1, so the form becomes y − 120 = 5(x − 64). All that’s left to do is simplify.
y − 120 = 5(x − 64)
y − 120 = 5x − 5·64
y − 120 = 5x − 320
y − 120 + 120 = 5x − 320 + 120
y = 5x − 200
You may think using the other point would give you a different equation, but that’s not the case. The equation will look different at first. If you used (67, 135) instead of (64, 120), you would start with y − 135 = 5(x − 67) instead of y− 120 = 5 (x − 64). That seems different, but when you simplify, it turns out to be the same equation.
y − 135 = 5(x − 67)
y − 135 = 5x − 335
y = 5x − 200
![]()
CHECK POINT
Find the slope of the line that passes through the two points given.
41. (6, 3) and (8, -7)
42. (-3, 5) and (1, 9)
43. (-4, -5) and (-1, -2)
44. (2, -4) and (-4, 8)
45. (7, 0) and (0, 7)
Find the equation of the line that passes through the two points given. Put the equation in point-slope form.
46. (5, -10) and (-5, 20)
47. (-4, -9) and (6, -4)
48. (4, -5) and (1, 7)
49. (3, 5) and (-3, 3)
50. 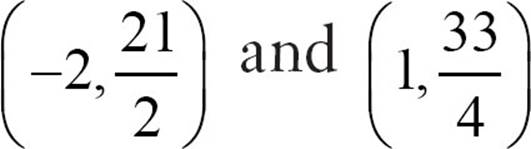
In a perfect world, you know the slope of your line and its y-intercept, drop them into slope-intercept form and you’re done. In a little less perfect world, you know the slope and a point, you plug them into point-slope form and simplify. But life is never perfect, so perhaps you only know two points, but you find the slope, plug a point and the slope into point-slope form and simplify. Ready for one last variant?
Parallel and Perpendicular Lines
Can you find the equation of a line parallel to y = 3x − 7? Remember, first of all, what parallel means. Two lines in a plane are parallel if they never intersect. They are always the same distance apart. In order for that to happen on a graph, the lines have to cross the plane at the same angle. They must have the same slope.
That’s actually helpful. If parallel lines have the same slope, a line parallel to y = 3x − 7 also has a slope of 3, but where is this line? You need to know some point to anchor the line. If you have a point for the line to pass through, and you can deduce that the lines have the same slope, a point and a slope are all the information you need.
So what’s the equation of a line that passes through (1, 1) and is parallel to y = 3x − 7? Parallel lines have the same slope so the slope is 3, and you can use point-slope form.
y − y1 = m(x − x1)
y − 1 = 3(x − 1)
y − 1 = 3x − 3
y = 3x − 2
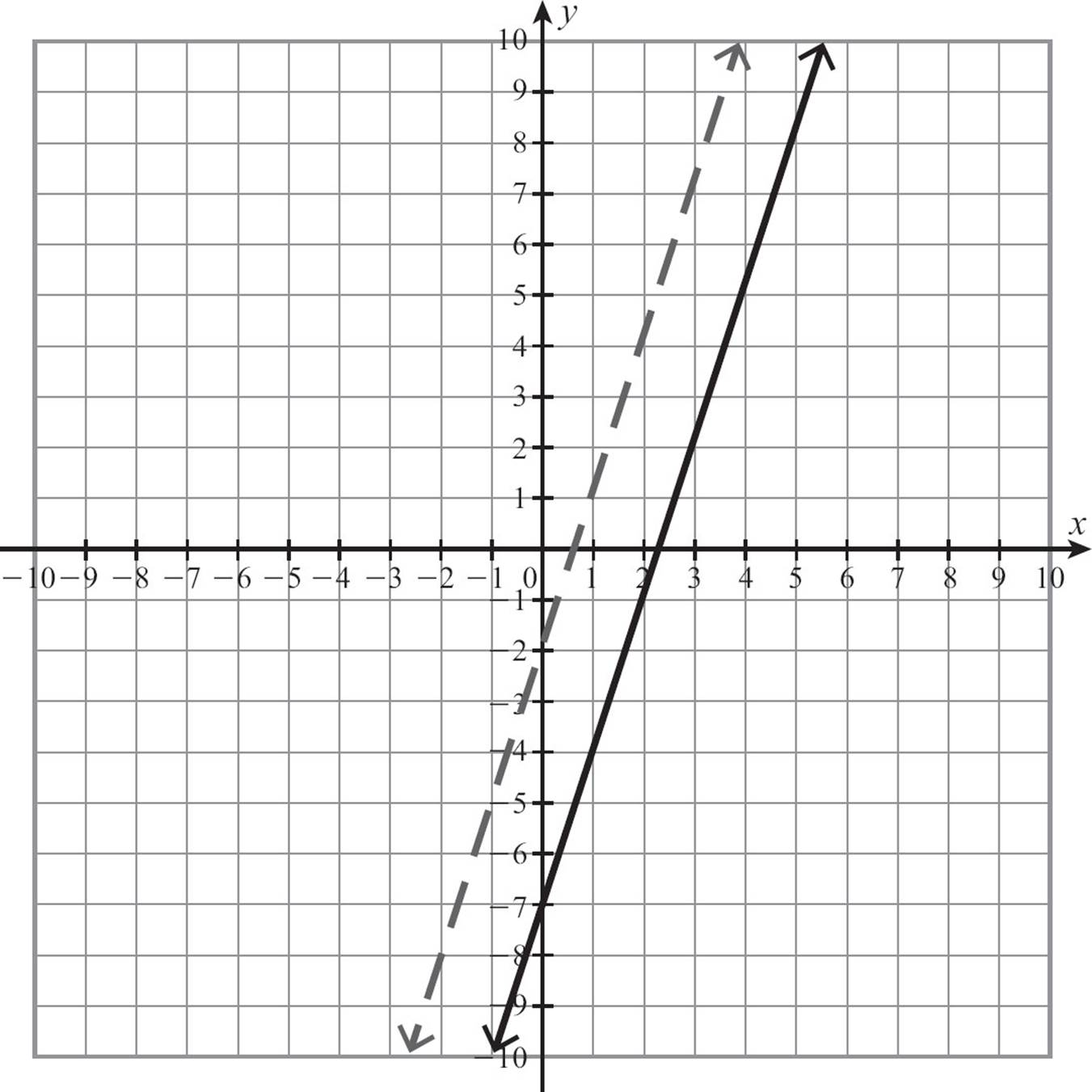
The line y = 3x − 2 passes through (1, 1) and is parallel to y = 3x − 7.
![]()
ALGEBRA TRAP
Parallel lines have the same slope, but before you decide what the slope of the given line is, be sure it’s in slope-intercept form. A line parallel to 2x − 3y = 6 doesn’t have a slope of 2, because 2x − 3y = 6 doesn’t have a slope of 2. When you put 2x − 3y = 6 in slope-intercept form, it becomes 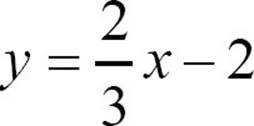 , and you can see the slope is really
, and you can see the slope is really ![]() .
.
How about a line perpendicular to y = −2x + 1? You’ll need a point to anchor this one, too. Let’s use (1, 1) again, but the slope isn’t quite so simple. Perpendicular lines, lines that meet at a right angle, don’t have the same slope. If they had the same slope, they’d be parallel and wouldn’t cross at all.
To create perpendicular lines, there would have to be one line that rises and one that falls, so the slopes would have to have opposite signs. The rises and runs have to be just right to get exactly a right angle. It turns out that perpendicular lines have slopes that are negative reciprocals. That means their slopes multiply to -1. If the slope of one line is 2, the slope of a line perpendicular to it is 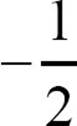 . If the slope of one line is
. If the slope of one line is 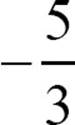 , a line perpendicular to it has a slope of
, a line perpendicular to it has a slope of ![]() .
.
![]()
Algebra Trap
If the slope of one line is 0, it’s impossible to find a negative reciprocal for the slope of the perpendicular, because division by 0 is impossible. But if the slope of one line is 0, the line is horizontal, and so a line perpendicular to it is vertical. The equation of a vertical line is x = a constant.
If you want a line that passes through (1, 1) and is perpendicular to y = −2x + 1, you can use a slope of ![]() and plug the point and the slope into point-slope form.
and plug the point and the slope into point-slope form.
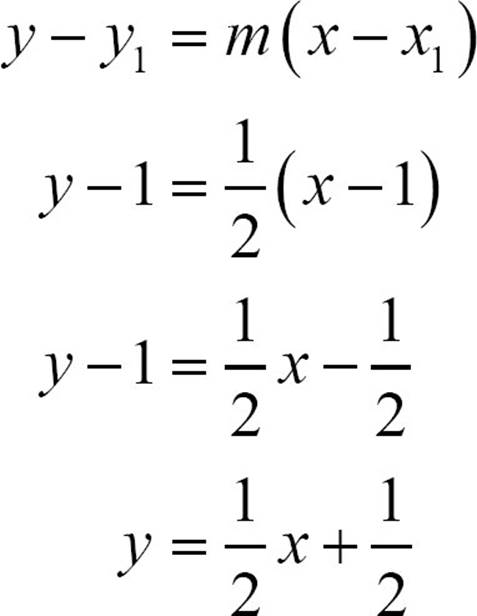
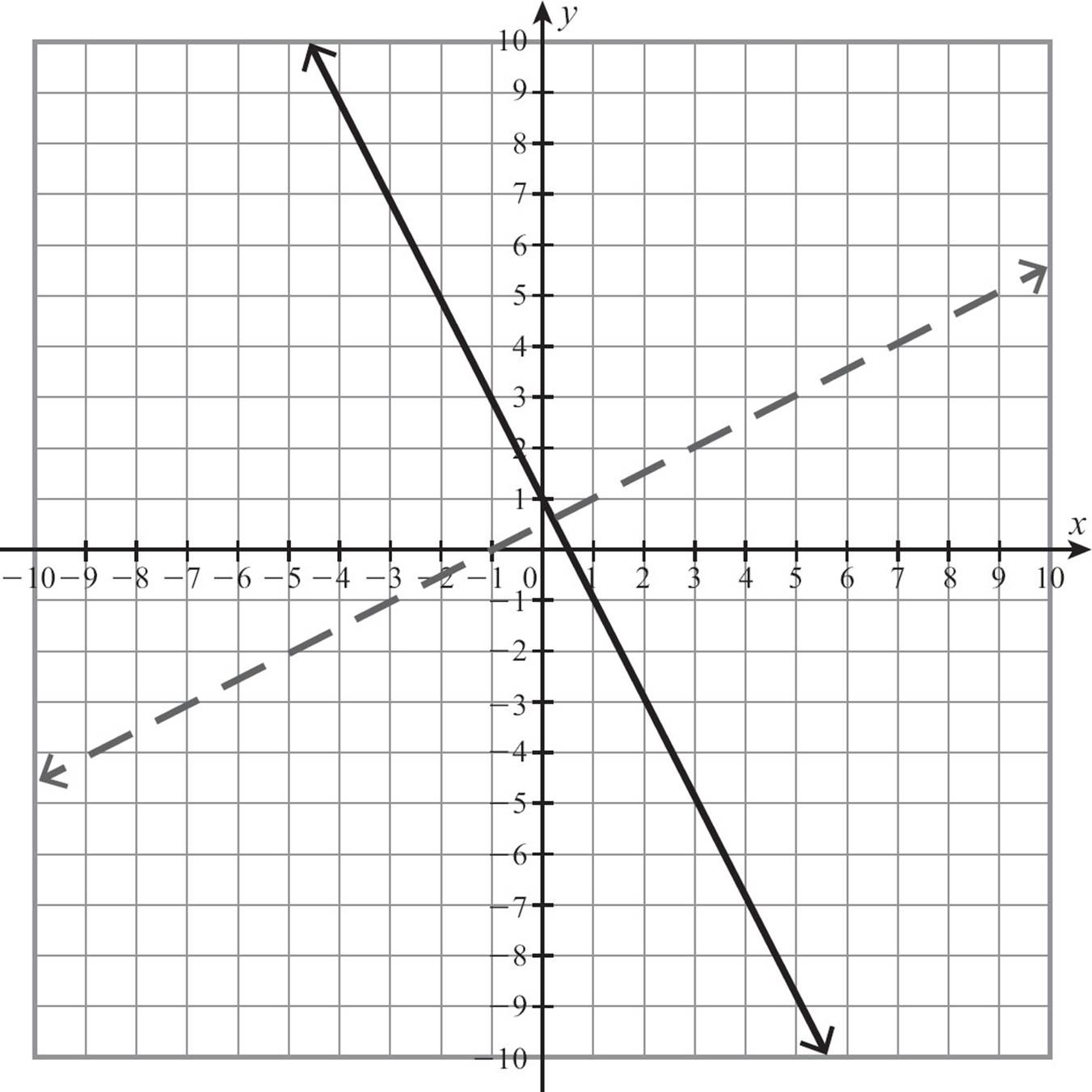
The line 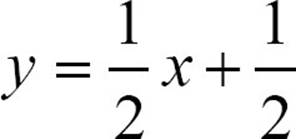 passes through (1, 1) and is perpendicular to y = −2x + 1.
passes through (1, 1) and is perpendicular to y = −2x + 1.
![]()
CHECK POINT
51. Find the equation of a line through the point (6, -3) parallel to y = 2x − 7.
52. Find the equation of a line through the point (-3, 2) parallel to 3y = x + 12.
53. Find the equation of a line through the point (-4, -3) parallel to y = 4x + 3.
54. Find the equation of a line through the point  parallel to y = −6x + 3.
parallel to y = −6x + 3.
55. Find the equation of a line through the point  parallel to
parallel to 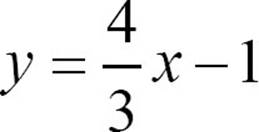 .
.
56. Find the equation of a line through the point (4, 7) perpendicular to y = 2x − 1.
57. Find the equation of a line through the point (6, -2) perpendicular to y = −3x + 5.
58. Find the equation of a line through the point (-1, 7) perpendicular to x − 2y = −12.
59. Find the equation of a line through the point 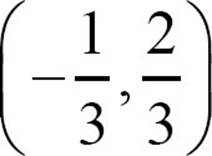 perpendicular to
perpendicular to 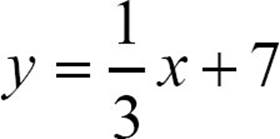 .
.
60. Find the equation of a line through the point (4, -3) perpendicular to y = x + 4.
The Least You Need to Know
· A linear equation can be written in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept, or in standard form, ax + by = c, where a, b, and c are integers and a is positive.
· Point-slope form, y − y1 = m(x − x1), can be used to create the equation of a line with slope m through point (x1,y1).
· If you know two points, (x1,y1) and (x2,y2), you can find the slope with the formula 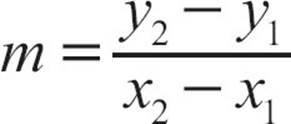 .
.
· Algebraic techniques can be used to change from one form to another.
· Parallel lines have the same slope. Perpendicular lines have slopes that are negative reciprocals.