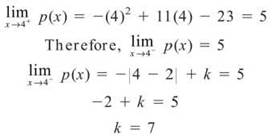Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 3. Limits and Continuity

CONTINUITY

I have had some bad experiences at the movies. Perhaps you have also—right at the good part of the film when everything’s getting exciting, the movie flickers off and the house lights come up. An usher informs the crowd that they are experiencing technical difficulties and that the movie should be up and running again in about 15 minutes. It ruins the whole experience, because the smooth, flowing, continuous stream of events in the film has been interrupted. In calculus, if a function experiences a break, then it, too, is said to be discontinuous. Any hole or jump in the graph of a function prevents the function from being classified as continuous. (Sometimes the sound in a theater prevents you from enjoying the film, but volume is not discussed until Chapter 9.)

NOTE. Classifying functions as continuous or discontinuous is important, because the continuity of a function is often a prerequisite for important calculus theorems.

Mathematically, a function f(x) is said to be continuous at x = a if all three of the following conditions are true:

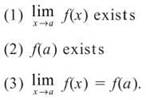
In other words, a function must be headed toward some height at x = a, and when you reach x = a, the function must actually exist at the height you expected.

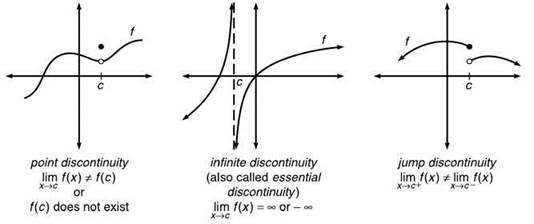
Three Types of Discontinuity

Example 4: On what intervals is continuous?

Solution: Visually, the graph is discontinuous at any hole or break, but a graphing calculator shows no obvious holes or breaks—it looks like a parabola. However, because g(x) is a rational (fractional) function, it will be undefined whenever the denominator equals 0. Thus, g(x) is discontinuous at x = —3, because g(—3) does not exist, and that breaks the second requirement for continuity. There must be a hole (or point discontinuity) in the graph at x = —3, even though it wasn’t obvious from the graph. So, the intervals of continuity for g(x) are (—∞,-3) ∪ (—3,∞). Note that x = —3 is the only discontinuity of the function—g is continuous at all other values of x.

In Example 4, it is still true that exists and is easily found (using the factoring method) to be 16, even though the function doesn’t exist there. What if you rewrote the function as follows?

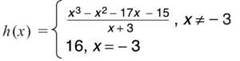
The new function, h, acts exactly as g did, except that h(—3) = 16. Redefining x = 3 “fixes” the discontinuity in g(x), satisfies the final two continuity conditions that g did not, and makes h a continuous function. Whenever you are able to redefine a finite number of points like this and make a discontinuous function continuous, the function is said to have had removable discontinuity. If it is not possible to “fix” the discontinuity by redefining a finite number of points, the function is said to be nonremovably discontinuous. If it is possible to “fix” the discontinuity, but you don’t feel like it, you are said to be a lazy bonehead.

Example 5: What type of discontinuity is exhibited by

Solution: Factor the denominator to get . Clearly, r is undefined for x = —2 and 2, and, hence, these are the discontinuities. Next, it is important to determine if and exist, because if a limit exists at a point of discontinuity, that discontinuity is removable. Remember: if no limit exists there, the discontinuity is nonremovable. Using the factoring method of evaluating limits,

TIP. Only point discontinuities are removable, because a limit exists.

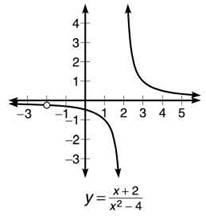
However, results in 1/0, which does not exist. Therefore, there is a point discontinuity at x = —2 and an infinite discontinuity at x = 2. The graph of the function verifies these conclusions.

TIP. Rational, polynomial, radical, exponential, trigonometric, and logarithmic functions are always continuous at all points in their domain. To help remember this, use the mnemonic device Red Parrots Continuously Repeat Everything They Learn.

Substitution is a shortcut method for classifying types of discontinuity of a function that typically works very well. In the previous example, you substituted x = 2 into r and got 1/0. In the shortcut, a number divided by zero suggests that a vertical asymptote exists there, making it an infinite (or essential) discontinuity (the two terms are interchangeable). Substituting x = —2 results in 0/0, which suggests point discontinuity.

Example 6: Find the value of k that makes f(x) continuous, given

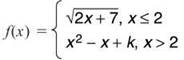
Solution: Because fix) is defined as a radical and a polynomial function, the two pieces of the graph will be continuous. The only possible discontinuity is at x = 2, where the graphs will have to meet. Otherwise, a jump discontinuity will exist. You know that f(2) = √11, according to the function. In order for a limit to exist at x = 2, the other rule in the function x² — x + k must also reach a height of √11 when x = 2.

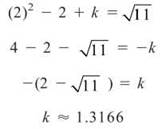
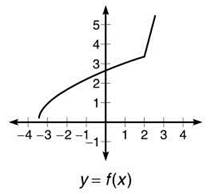
The graph below of f(x) visually verifies our result—no holes, gaps, or jumps when x = 2:

EXERCISE 3

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

DO NOT USE A GRAPHING CALCULATOR FOR ANY OF THESE PROBLEMS.

For problems 1 through 3, explain why each function is discontinuous and determine if the discontinuity is removable or nonremovable.

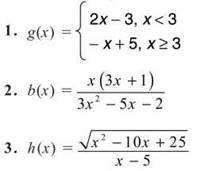
4. Describe the continuity of the 15 functions you were to memorize in Chapter 2 without consulting any notes.

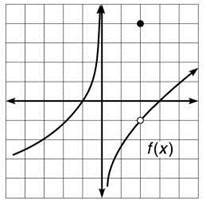
5. Draw the graph of a function, f(x), that satisfies each of the following conditions. Then, describe the continuity of the function:

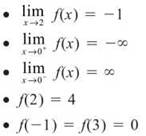
• f increases on its entire domain

6. Find the value of k that makes p continuous if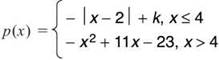

ANSWERS AND EXPLANATIONS

1. g is made up of two polynomial (linear) segments, both of which will be continuous everywhere. However, the graph has a jump discontinuity at x = 3. Notice that (you get this by plugging 3 into the x < 3 rule). The right-hand limit of g(x) at x = 3 is 2. Because the left- and right-hand limits are unequal, no general limit exists at x = 3, breaking the first condition of continuity. Furthermore, because no limit exists, the discontinuity is nonremovable.

2. Because b is rational, b will be continuous for all x in the domain. However, x = —1/3 and 2 are not in the domain. Using the factoring method of evaluating limits, you get that , so x = —1/3 is a removable discontinuity. No limit exists at x = 2, an essential discontinuity.

3. The numerator of the fraction is a perfect square, so simplify to get

Remember that the square root function has a positive range, so the numerator must be positive:

It helps to think about this graphically. After substituting some values of x into h, you get the following graph:

Thus, h has a jump discontinuity at x = 5.

4. y = x: continuous on (—∞,∞)

y = x²: continuous on (—∞,∞)

y = x³: continuous on (—∞,∞)

y = √x continuous on [0,∞)

y = |x|: continuous on (—∞,∞)

y = 1/x: continuous on (—∞,0) ∪ (0,∞)

y = [[x]]: continuous for all real numbers x, if x is not an integer

y = e^x: continuous on (—∞,∞)

y = ln x: continuous on (0,∞)

y = sin x: continuous on (—∞,∞)

y = cos x: continuous on (—∞,∞)

y = tan x: continuous for all real numbers x, if (which can also be written , when n is an integer)

y = cot x: continuous for all real numbers x if x ≠ ..., —π,0,π,... (which can also be written x ≠ nπ, when n is an integer)

y = sec x: continuous for all real numbers x, , when n is an integer

y = esc x: continuous for all real numbers x, x ≠ nπ, when n is an integer

5. There is some variation in the possible answer graphs, but your graph should match relatively closely.

6. Just like Number 1 in this problem set, the x < 4 rule evaluated at 4 represents , and the x > 4 rule evaluated at 4 represents . In order for p to be continuous, these limits must be equal.