Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 3. Limits and Continuity
HANDS-ON ACTIVITY 3.3: THE INTERMEDIATE VALUE THEOREM
Much like the Extreme Value Theorem guaranteed the existence of a maximum and minimum, the Intermediate Value Theorem guarantees values of a function but in a different fashion. Once again, continuity is a cornerstone of this theorem.
1. Consider a continuous function f(x), which contains points (1,-4) and (5,3). You are not given an equation that defines f(x)—only these points.
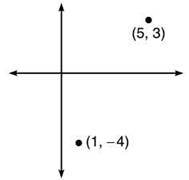
Draw one possible graph of f(x) on the axes above.
2. Decide which of the following must occur between x = 1 and x = 5. Justify your answer.
(A) maximum
(B) minimum
(C) root
(D) y-intercept
_____________________________________________________
_____________________________________________________
3. Which of the following height(s) is the function guaranteed to reach, and why?
(A) -5
(B) -1
(C) 2
(D) 5
_____________________________________________________
_____________________________________________________
4. Draw three different graphs off(x) that are discontinuous and, therefore, do not fulfill the conclusion you drew in Number 2.
5. Based on your work above and the diagram below, complete the Intermediate Value Theorem below.
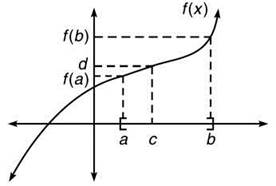
Intermediate Value Theorem: Given a function f(x) that is ______ on the interval ______, if d is between ______ and ______, then there exists a c between ______ and ______ such that f(c) = ______.
6. Rewrite the Intermediate Value Theorem in your own words to better illustrate its meaning.
_____________________________________________________
_____________________________________________________
7. Give one real-life example of the Intermediate Value Theorem’s guarantees.
_____________________________________________________
_____________________________________________________
ALERT! The Intermediate Value Theorem guarantees that I will hit each intermediate height at least once. Note that in my solution for problem 1, fhas 3 roots, although only 1 was guaranteed.
SOLUTIONS TO HANDS-ON ACTIVITY 3.3
1. There are many possible answers, but here’s one:
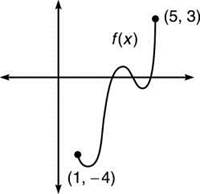
2. The correct answer is (C), root. If the function is continuous, it must cross the x-axis at some point in the interval. A continuous function will have both a minimum and maximum value. If the function begins with negative values at x = 1 but eventually has positive values at x = 5, the function had to equal zero (change from positive to negative) somewhere in [1,5].
3. Much like the function must reach a height of zero (as described in Number 2 above), the function must also reach all other heights between —4 and 3. Thus, the answer is both (B) and (C).
4. There are numerous ways to draw discontinuous functions that will not reach a height of zero. Below are three possible graphs. This highlights the importance of f(x) being continuous.
5. Given a function f(x) that is continuous on the interval [a,b], if d is between f(a) and f(b), then there exists a c between a and b such that f(c) = d.
6. If a continuous function begins at height f(a) when x = a and ends at height f(b) when x = b, then the function will cover every single height between f(a) and f(b) at some x between a and b.
7. If I am two feet tall when I am 18 months old and 6 feet tall when I am 27 years old, then at some age between 18 months and 27 years, I was 4 feet tall. (In fact, since height according to age is continuous—you don’t suddenly jump from 3 to 4 feet tall—I will cover all heights between 2 and 6 feet sometime in that time interval.)
EXERCISE 5
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
DO NOT USE A CALCULATOR FOR PROBLEMS 1 AND 2.
1. On what interval must the function g(x) = 2x2 + 7x — 1 intersect the line y = 7?
(A) [-8,-6]
(B) [-4,-1]
(C) [0,2]
(D) [6,9]
2. Given a function h(x) continuous on [3,7] with h(3) = 1 and h(7) = 9, which of the following must be true?
I. There exists a real number p such that h(p) = 5,1 < p < 9
II. h(5) = 5
III. h has a maximum and a minimum on [3,7]
(A) I only
(B) III only
(C) I and III
(D) I, II, and III
YOU MAY USE YOUR CALCULATOR FOR PROBLEM 3.
3. Given the continuous function f(x) = ln (—x) + cos x, prove that there exists a c ∈ [—π,—π/2] such that f(c) = .240 and find c.
ANSWERS AND EXPLANATIONS
1. This question is only the Intermediate Value Theorem (IVT) rephrased. Using the terminology of problem 5 from the hands-on exercise, 7 is the d value between g(a) and g(b). Each of the interval choices is a candidate for [a,b]. You should plug each pair into the function to see if the resulting pair f(a) and f(b) contains 7. Choice (C) results in f(a) = —1, f(b) = 21. Clearly, 7 falls between these numbers; this is not true for any of the other intervals.
2. It helps to draw the situation in order to visualize what’s being asked.
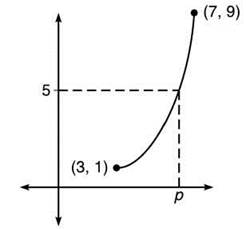
The correct answer is (C). Statement I is true. The IVT guarantees that p will exist on the interval [3,7]. So, if p exists on [3,7], p will definitely exist on [1,9], as [3,7] is merely a subset of [1,9]. Statement II is not always true; in fact, it’s not true in the representation of h in the diagram above. Statement III is true by the Extreme Value Theorem since h is continuous on a closed interval.
3. To apply the IVT (the prerequisites of the theorem are met as f is continuous on a closed interval), you note that f(—π) ≈ .1447 and f(—π/2) ≈ .4516. As .240 falls between these values, a c ∈ [—π,—π/2] such that f(c) = .240 is guaranteed. To find c, set f(x) = .240 and solve with your calculator; c = —2.0925.