Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 2. Calculus Prerequisites

OVERVIEW

• Functions and relations

• Function properties

• Inverse functions

• Hands-On Activity 2.1: Transforming functions

• Trigonometry

• Parametric equations (BC topic only)

• Polar equations (BC topic only)

• Vectors and vector equations (BC topic only)

• Technology: Solving equations with a graphing calculator

• Summing it up

This chapter is meant to help you review some of the mathematics that lead up to calculus. Of course, all mathematics (and your entire life, no doubt) up until this point has simply been a build-up to calculus, but these are the most important topics. Since the focus of this book must be the actual content of the AP test, this chapter is meant only to be a review and not an in-depth course of study. If you find yourself weak in any of these areas, make sure to review them and strengthen your understanding before you undertake calculus itself. Ideally, then, you should plod through this chapter early enough to address any of your weaknesses before it’s too late (read with a scary voice).

FUNCTIONS AND RELATIONS

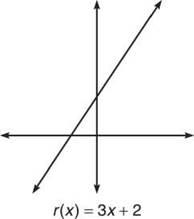
Calculus is rife with functions. It is unlikely that you can find a single page in your textbook that isn’t bursting with them, so it’s important that you understand what they are. A function is a special type of relation, much as, in geometry, a square is a special type of rectangle. So, in that case, what is a relation? Let’s begin with a simple relation called r. We will define r as follows: r(x) = 3x + 2. (This is read “r of x equals 3 times x plus 2.”) Our relation will accept some sort of input (x) and give us something in return. In the case of r, the relation will return a number that is two more than three times as large as your input. F or example, if you were to apply the rule called r to the number 10, the relation would return the number 32. Mathematically, this is written r(10) = 3(10) + 2 = 30 + 2 = 32. Thus, r(10) = 32. We say that the relation r has solution point (10,32), as an input of 10 has resulted in an output of 32.

Example 1: If g(x) = x² — 2x + 9, evaluate g(4) and g(—3).

Solution: Simply substitute 4 and —3 in for x, one at a time, to get the solutions:

g(4) = (4)² - 2(4) + 9 = 16 - 8 + 9 = 17

g(-3) = (-3)² - 2(-3) + 9 = 9 + 6 + 9 = 24

We call g and r relations because of the way they relate numbers together. Clearly, r related the input 10 to the output 32 in the same way that g related 4 to 17 and —3 to 24. It is conventional to express these relationships as ordered pairs, so we can say that g created the relationships (4,17) and (-3,24).

There are numerous ways to express relations. They don’t always have to be written as equations, though most of the time they are. Sometimes, relations are defined simply as the sets of ordered pairs that create them. Here, we have defined the relation k two ways that mean the same thing:

k: {(-3,9),(2,6),(5,-1),(7,12),(7,14)}

You can also express a relation as a graph of various ordered pairs that create it, in the form (x,y). Below we have graphed the function we defined earlier, r(x) = 3x + 2.

Sometimes, the rule for a relation changes depending on the input of the relation. These are called piecewise-defined relations or multi-ruled relations.

Example 2: Graph the piecewise-defined relation and evaluate h(—2), h(—1), h(0), h(2), h(2.5), and h(6).

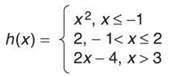
Solution: The graph begins as the parabola x², but once x = —1, the new rule takes over, and the graph becomes the horizontal line y = 2. This line stops, in turn, at x = 2. The function is undefined between x = 2 and x = 3, but for all x > 3, the line 2x - 4 gives the correct outputs.

Note: If you didn’t recognize that y = x² is a parabola, that’s OK (for now). Later in the chapter, we discuss how to recognize these graphs.

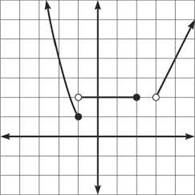
h(—2) = (—2)² = 4, since —2 falls within the definition of the first of the three rules.

h(— 1) = (—1)² = 1, for the same reason.

h(0) = 2, as 0 is between —1 and 2, the defined region for the second rule.

h(2) = 2, as it just falls within the definition of the second rule.

h(2.5) is not defined for this function—no inputs between 2 and 3 are allowed.

h(6) = 2(6) — 4 = 8, since 6 > 3, the defining restriction for the last rule.

So, a relation is, in essence, some type of rule that relates a set, or collection, of inputs to a set of outputs. The set of inputs for a relation is called the domain, whereas the set of outputs is called the range. Often, it helps to look at the graph of the relation to determine its domain and range, as the x values covered by a graph represent its domain, and the y values covered by a graph represent its range. Alternatively, you can think of the domain as the numbers covered by the “width” of the graph, and the range as the numbers covered by the “height” of the graph.

Example 3: Find the domain and range for the relations k and h, as already defined above.

Solution: Finding domain and range for k is quite easy. The domain is {—3,2,5,7} and the range is {—1,6,9,12,14}. The order of the numbers does not matter in these sets. The domain of h comes right from the relation—written in interval notation, the domain is (—∞,2] ∪ (3,∞). This is true because any number up to or including 2 is an input for the relation, as is any number greater than 3. The range is easily determined from the graph we created already. Look at the height or vertical span of the graph. Notice that it never dips below a height of 1, but above 1, every single number is covered. Even though there are holes in the graph at (—1,2) and (3,2), the height of 2 is covered by numerous other x values. Thus, the range of the graph is (1,∞).

Now that you know quite a bit about relations, it’s time to introduce functions. Functions are simply relations such that every input has a unique output. In other words, every element of the domain must result in only one output.

Example 4: Which of the relations, r, g, and k, as defined in the preceding examples, are functions?

Solution: Take r as an example. When you evaluated r(10), the result was 32. Is there any chance that something other than 32 could result? No. In a similar fashion, any number, when substituted for r, will result in only one output. Thus, r is a function. Similarly, g is a function. However, k is not a function, since k(7) = 12 and 14. Because the domain element 7 results in two range elements, 12 and 14, k is not a function. Consider what’s happening in function k graphically:

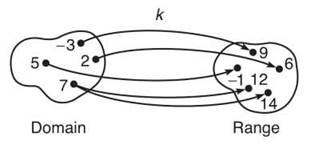
Graphically, the road (or map) from 7 in the domain to the range forks, whereas the inputs —3, 2, and 5 have only one path to follow. Because of this fork in the road from 7, k is not a function.

Often, it is unfruitful to ponder whether or not a relation is a function merely by remembering the definition. A shortcut to determining whether or not a given relation is a function is the vertical line test. To use this test, imagine vertical lines passing through the graph of the relation. If any vertical line you could possibly draw intersects the graph in more than one place, the relation is not a function. If any vertical line resembles former U.S. President James K. Polk, seek professional help.

Example 5: Explain why the relation described by the equation x² + y² = 9 is not a function.

Solution: First, you need to remember that x² + y² = 9 is the equation of a circle centered at the origin with radius 3. Look at the graph of the relation:

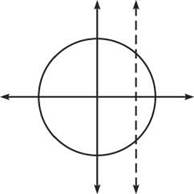
Notice the line x = 2 (one of many vertical lines you could imagine intersecting the graph) intersects the circle in two places. By substituting 2 for x in the equation, you can determine that the two points of intersection are (2,√5) and (2,—√5). Since x = 2 has two distinct outputs, this is not a function.

Even if you weren’t sure what a function was by definition, you undoubtedly know many functions already. You should know, at the minimum, 15 specific functions and their properties by heart. Nine of these are listed below with any important characteristics you should either memorize or be able to determine from the graph. The remaining six are presented later in this chapter. These functions and their defining characteristics need to become really familiar to you.

NOTE. The other six functions are given in the trigonometry section of this chapter.

ALERT. [[-4.9]] ≠ -4. The answer cannot be -4 since -4 is larger than -4.9, and the greatest integer function outputs the largest integer less than or equal to the input. [[-4.0]] = -5.

Important Functions to Memorize

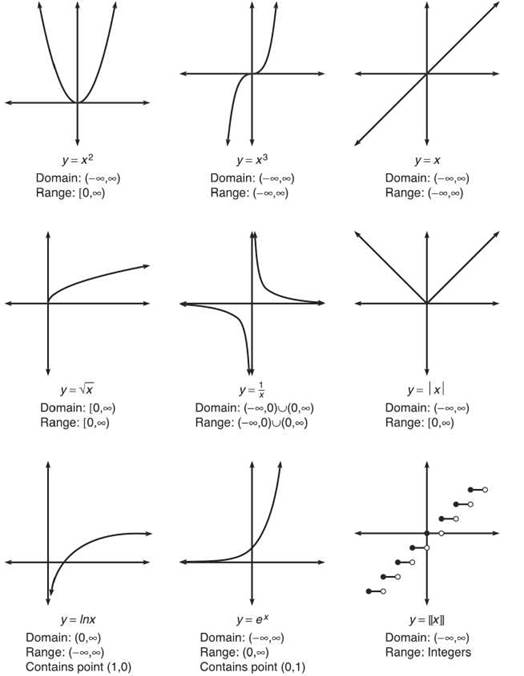
Among these functions, the strangest might be y = [[x]], called the greatest integer function. This function takes any real number input and returns the largest integer that is less than or equal to it. For example, [[5.3]] = 5 since among the integers that are less than or equal to 5.3 (5,4,3,2,1,0,—1,—2,...), the largest is 5. Likewise, [[4]] = 4. However, [[—3.6]] = —4, since among the integers less than —3.6 (—4,—5,—6,—7,...), —4 is the largest.

EXERCISE 1

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 3 THROUGH 6.

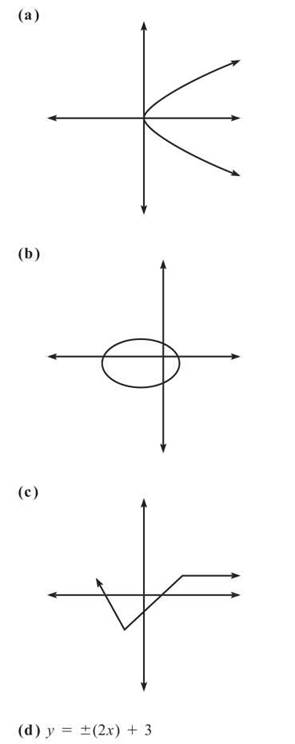
1. Which of the following relations are functions?

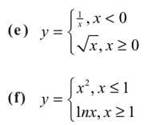
what is the domain of h?

find f(4) - g(3) + (fg)(0)

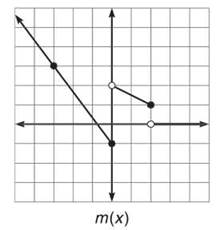
Write the function, m, whose graph is given below. Also, find the domain and range of m.

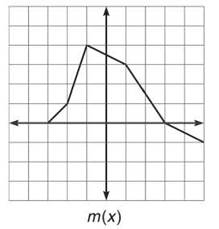
5. If m(x) is defined by the graph below, evaluate [[m(—3)]], [[m(0)]], and [[m(4)]].

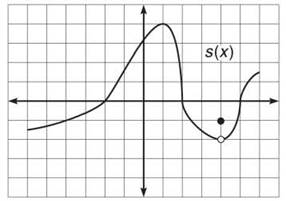
6. Graph some function s(x) such that

• s(1) = 4

• s(-2) = s(2) = s(5) = 0

• s is increasing on [—6 < x < 1 and 4 < x < 6]

• s has domain [—6,6] and range (—2,4]

ANSWERS AND EXPLANATIONS

1. Only c and e are functions. Notice that a, b, and f (when graphed) fail the vertical line test. In d, every input except zero will result in two outputs.

2. According to the problem, When the denominator is zero, the function is undefined (since it is illegal in this arm of the Milky Way to divide by zero). Factoring the denominator gives (x + 4)(x + 5), which means that function is undefined when x = —4 or x = —5. Thus, the domain of h is all real numbers except —4 and —5.

3. The function (fg)(x) is created by the product of f and g. Since Thus, or, approximately 5.218.

4. By examining the slopes and y-intercepts of these lines, it is not too hard to get the piecewise-defined function.

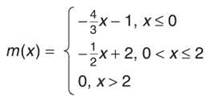
The domain of m(x) is (—∞,∞), and the range is (—1,∞).

5. From the graph, you can see that m(—3) = 0, m(0) = 3.5, and m(4) = —.5, so the greatest integer function values are not too difficult: [[m(—3)]] = 0, [[m(0)]] = 3, and [[m(4)]] = -1.

6. There are a number of solutions to the problem. One is given here: