Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 6. Applications of the Derivative

MOTION IN THE PLANE (BC TOPIC ONLY)

Although these questions are less frequent, the AP test sometimes contains questions concerning movement along a parametrically defined or vector path. Vector defined functions are quite easy to differentiate, making this topicrelatively simple in the grand scheme of BC topics. Before you read on, you should look back at the introduction to vector functions in Chapter 2.

In order to differentiate a vector function s = f(t)i + g(t)j, find the derivatives of the components separately:

Vector position equations work similarly to the position equations we just discussed. The velocity vector is given by the first derivative of the position equation, and the acceleration vector is given by the second.

Example 7: A particle moves in the plane such that the position vector from the origin to the particle is

s = (cos t sin 2t)i + (2t + 1)j, for all t on the interval [0,2π]

(a) Find the velocity and acceleration vectors for any time t.

To find the velocity vector, take the derivative of the x and y components separately:

v = (2cos t cos 2t - sin t sin 2t)i + 2j

In order to find the acceleration vector, take the derivative again:

a = (—4cos t sin 2t — 2sin t cos 2t — 2sin t cos 2t — cos t sin 2t)i

(b) What is the velocity vector when t = π/2, and what is the speed of the particle there?

Plug t = π/2 into the velocity vector to get the specific answer for that value of t:

v = (0 ∙ —1 — 1 ∙ 0)i + 2jv = 2j

The graph and its velocity vector at t = π/2 are shown below. The velocity vector has no horizontal component because the graph is changing direction at that point (kind of like a sideways extrema point).

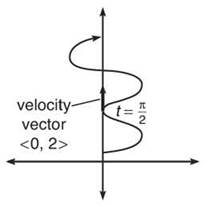
The speed of the particle is given by the norm of the velocity vector. Remember, you find the norm with the equation

In this case

EXERCISE 6

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

YOU MAY USE YOUR GRAPHING CALCULATOR FOR PART (B) OF PROBLEM 1 AND ALL OF PROBLEMS 2 AND 3.

1. A particle moves along the graph defined by x = cos t, y = cos 31, for t on the interval [0,2π].

(a) What is the velocity vector, v, when ?

(b) Draw the path of the particle on the coordinate plane, and indicate the direction the particle moves. Draw the velocity vector for .

(c) What is the magnitude of the acceleration when ?

2. A particle moves along a continuous and differentiable path that includes the coordinates (x,y) below for the corresponding values of t:

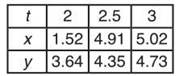
Approximate the speed of the particle at t = 3.

3. Create a position equation in vector form for a particle whose speed is 15 when t = 1.

ANSWERS AND EXPLANATIONS

1. (a) The general position vector is given by s = (cos t)i + (cos 3t)j. Therefore, the velocity vector will be v = (—sin t)i + (—3sin 3t)j. The velocity vector when will be since which is coterminal with 5π/4.

b)

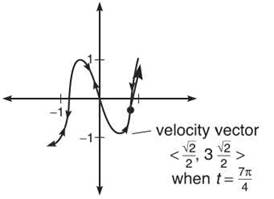
The graph proceeds from (1,1) to (-1,-1) on [0,π] and then returns to (1,1) on [π,2π].

(c) The magnitude of the acceleration is found by calculating the norm of the acceleration, much like the speed is the magnitude (norm) of the velocity. Therefore, you should begin by finding the acceleration vector by differentiating the velocity vector:

a = (—cos t)i + ( —9cos 3t)j

The magnitude of the acceleration is the norm of that vector, so calculate it when :

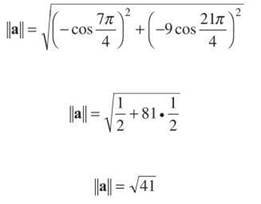
2. Recall the generic formula for speed as the norm of velocity: Because you do not have the position vector, you cannot find v. However, you can use slopes of secant lines to approximate dx/dt and dy/dt:

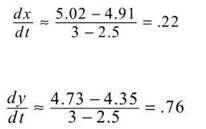
Therefore,

3. From the given information, we know that

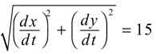
so therefore,

There are numerous approaches to take, but we will discuss the easiest. Because we can do anything we like (as long as it works), we’ll set dx/dt = 15 and dy/dt = 0. Notice that the sum of their squares equals our goal. Next, we need an expression for x whose derivative, evaluated at 1, is 15. What about x = 15/2t²? The trick is taking half of the number you want to end up with and using it as the coefficient, since the Power Rule dictates that you will multiply by 2: Clearly, this has a value of 15 when t = 1. You can use any constant for your y component, since its derivative will be 0. One possible answer for this problem, therefore, is Check it to convince yourself that it’s right.