Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 6. Applications of the Derivative

OPTIMIZATION

Optimization, like related rates, is one of the most useful topics in calculus because of its direct tie to real-world applications. However, just like related rates, it is one of the topics many students forget about by test time. There are many theories that could account for this forgetfulness in students. One theory is that related rates and optimization, unlike many other calculus topics, require students to follow a strict algorithm in order to arrive at a correct answer (you must proceed from one step to the next, and there are fewer alternative solutions possible than in other calculus topics).

Another less widely held theory is that the concepts of related rates and optimization are imprinted on smaller “memory molecules” than other calculus topics. These smaller molecules are, then, shaken loose from the brain and escape through small lesions in its surface every time you sneeze. I, myself, am torn as to which is actually true, but it does explain the common student phrase “Good luck on the AP Calculus test, and try not to sneeze,” which has puzzled scholars for decades.

NOTE. The entire concept of optimization is based on our ability to find max’s and min’s using critical numbers and wiggle graphs.

Optimization is the process of finding an optimal value, either maximum or minimum, under strict conditions. You may be asked to minimize area, maximize volume, minimize cost, or maximize profit, just to name a few applications. But, we will start out with a simpler example.

Example 8: What two positive real numbers give the smallest possible product if one number is two less than three times the other?

Solution: The first step in an optimization problem is to design an equation that represents what you are actually trying to optimize. In this case, you want the minimum product of two numbers.

We will set up the equation

P = xy

which simply means that some product P is equal to two different numbers, x and y, multiplied. We want a minimum value for P. One problem stands in our way. Optimization problems require a single variable in the expression. We have two variables, so we need to go back to the original problem for more information. There is another relationship between the variables: one (it doesn’t matter which) is two less than three times the other, so we can write:

y = 3x — 2

Now, substitute this y value into our original equation for P to get

P = x ∙ (3x — 2) = 3x² — 2x

We now have an equation for the product in a single variable! Do you realize how wonderful that is? We already know how to find a maximum or minimum—take the derivative and construct a wiggle graph:

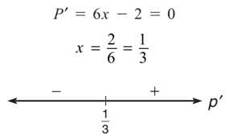
TIP. You can tell that this is an optimization problem because it asks for the “smallest possible” number. If the problem is asking for an extreme value (whether large or small), it’s an optimization problem.

From the wiggle graph, it is simple to see that the function P will have a minimum when x = 1/3. What is the corresponding v? Plug it back into our secondary equation y = 3x — 2:

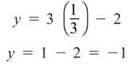
Therefore, the numbers —1 and 1/3 have the smallest possible product, given our initial defining condition of one being two less than three times the other (—1 is 2 less than 3 ∙ 1/3).

To be honest, this looks like a complicated process, but the method is really quite straightforward and repetitive.

3 Steps for Success with Optimization Problems

1. Write an equation that represents what you are trying to maximize or minimize (this is called the primary equation).

2. If more than one variable is present, use other information in the problem (in the form of secondary equations like y = 3x — 2 in Example 8) to eliminate the excess variables.

3. Find the derivative of your primary equation so that you can identify the critical numbers and draw a wiggle graph to find the answer.

If you remember these steps, you are well on your way to succeeding at optimization problems.

Example 9: What point on the graph of y = sin x is the closest to (0,1)?

Solution: You are trying to minimize distance, so use the distance formula as your primary equation:

ALERT! Because optimization problems have numerous steps, students sometimes stop too early and don’t actually answer the question posed to them. When you’re done, reread the question and make sure you’ve answered it.

Although it doesn’t matter which is which, we’ll set (x₁,y₁) equal to the stationary point (0,1) and set (x₂,y₂) equal to the point on the graph of sine (x, sin x). Substitute these points in to get

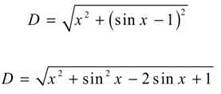
Time to find the derivative and set it equal to zero to find critical numbers:

The critical number will he x = .4787224241. You have to graph the derivative to find this value, so while you have D' on your calculator screen, notice that it is negative before the critical number and positive after. Therefore, x = .4787224241 is a minimum. (This is a quick calculator shortcut for constructing wiggle graphs without the tedious test point substitution.) In order to finish the problem, however, we need to give the coordinate that is closest to sin x, so plug x into sin x to get the y value. The final answer is (.479,.461).

NOTE. By the way, 100 in³ is a freakin’ lot of Schwop! In fact, there is so much beverage in each can that consumers have coined the phrase Schwop! buckets when referring to your product.

Example 10: You have invented a new and delicious beverage called Schwop!, which tastes inexplicably like cotton balls. Deemed the least refreshing drink in the known universe, it is nonetheless flying off the shelves. If you wish each cylindrical can of Schwop! to contain 100 in³ of beverage, what height must each can be to minimize the amount of aluminum you use to manufacture the cans?

Solution: Each can is made up of a rectangle and two circles (you can’t forget the top and bottom of the can!), as shown below:

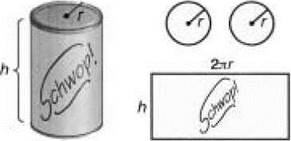
The construction of a can of Schwop!

You first need to write an equation representing what you want to minimize (aluminum), which in this case is the surface area of the can plus the area of the top and bottom of the can:

A = 2 πrh + 2 πr²

NOTE. The top of the Schwop! can has circumference 2πr, which is why the rectangle of aluminum has that as its length when the can is cut apart.

Danger! There are two variables present. To rectify this, use the other information given by the problem—the volume of Schwop! in each can:

V = πr²h = 100

You can solve this for h to eliminate that pesky extra variable:

Substitute back into the original equation to get

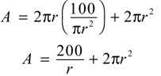
As is typical of optimization problems, the hardest part was finding the equation; now, find the derivative and set up a wiggle graph:

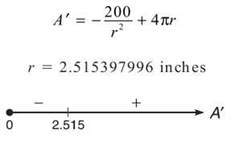
This is the radius of the smallest possible can. Be careful—the problem does not ask for this value. It asks for the height that corresponds to it. That height is

EXERCISE 7

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 2 THROUGH 4.

1. (A classic maximization problem) Farmer Rogendoger breeds cows that can’t swim. “Nonbuoyant cows just taste better, dadgum it, ”he insists (and it’s best not to question him further). Because the cows are landlocked, it saves him fence costs. If Rogendoger sets up a rectangular pasture that is bordered on one side by a river (which requires no fence, for obvious reasons), what is the maximum area he can enclose with 1,000 feet of fence? (Food for thought: Flow does he prevent cattle theft by riverboat-riding marauders?)

2. What point(s) on the graph of y = cot x is closest to the coordinate pair (π,0)?

3. Find the maximum area of a rectangle that has two vertices on the x-axis and two vertices on the graph of y = x² — 8.

4. To celebrate our first anniversary, I am commissioning the construction of a four-inch-tall box made of precious metals to give to my bride, Lisa. The jewelry box will have rectangular sides and an open top. The longer sides of the box will be made of gold, at a cost of $300/in²; the shorter sides will be made of platinum, at a cost of $550/in². (Let’s call it practical, not cheap, that the shorter sides are more expensive). The bottom will be made of plywood, at a cost of $.02/in². What dimensions provide me with the lowest cost if I am adamant that the box have a volume of 50 in³?

ANSWERS AND EXPLANATIONS

1. You should begin this problem with a diagram, including all relevant information, like so:

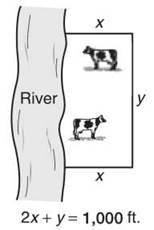
You want to maximize the area, so your primary equation must be the area of the rectangle: A = xy. However, there are two variables, so consider the secondary equation based on the limited amount of fence: 2x + y = 1,000 (it’s not 2x + 2y because you don’t need to fence the river). Solve the secondary equation for y to get y = 1,000 — 2x and substitute that into the area equation:

A = x(1,000 - 2x) = 1,000x - 2x²

Now, find the maximum of this equation through the usual channels:

The optimum value for x is 250, and the corresponding y will be

y = 1,000 - 2(250) = 500

Therefore, the maximum area is 500 ∙ 250 = 125,000 ft². As far as the riverboat marauders, answers may vary.

2. This is similar to Example 9, so there’s no need to go into a great deal of detail here. Use the same process with points (π,0) and (x, cot x):

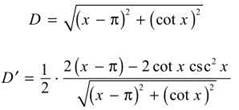
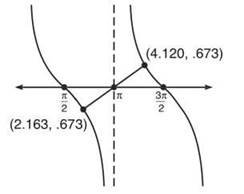
There are two critical numbers to worry about, since only two of them are close to (π,0): 2.163306396 and 4.119878911. (Don’t forget that π is also a critical number since cot x is undefined there.)

In order to figure out which is closer, you’ll need to plug them both into the distance formula. Remember, we have designed this formula to tell us how far away something is from (π,0) merely by substituting in the x value. It turns out that they both are a distance of 1.187534573 units away, so both are correct answers. The problem does ask for points however, so plug both x values (don’t round until the very end!) into cot x to get your final answer of (2.163, —.673) and (4.120,.673), shown below.

3. You should again begin by drawing a picture:

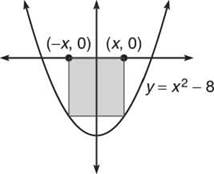
Because the parabola is y-symmetric, our rectangle should be, too, in order to maximize area. The width of the rectangle in the diagram is 2x, and its length is —f(x), if we set/(x) = x² — 8. This is because /(x) will be negative, and you don’t want a negative length. Your overall goal is to maximize area, so your equation should be the area of a rectangle:

A = l ∙ w

A = -(x² - 8)(2x) = -2x³ + 16x

Only one variable is in the equation, so proceed as planned, and critically wiggle:

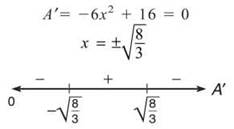
Therefore, is the optimum value for x, so the maximum width of the rectangle is The corresponding length will be 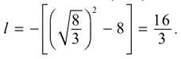Finally, the maximum area will be

4. Below is a graphic representation of the box in question:

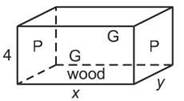
As drawn, the side toward you and in the back are the larger, gold sides, and the left and right sides are the smaller, platinum sides. In addition, x represents the length of the gold side and y represents the length of the platinum side. As stated in the problem, the height of the box is 4 inches. Remember that your overall goal is to find the minimum cost, so you need to design a cost equation based on how expensive the box will be to create. To do so, find the area of each side of the box, and multiply it by how expensive the materials would be for that side. For example, the side facing you is made of gold and has an area of 4*. Therefore, the cost of the side will be 4x ∙ 300. There are two of those sides, so you multiply by two to get 2,400x. Finally, add in the platinum sides and the bottom to get

C = 2,400x + 4,400y + xy(.02)

Something’s wrong—there are two variables. Time to use the last bit of information from the problem: the box must have a volume of 50 in³. That is written as 4xy = 50. If you solve for y, you get y = 25/2x. Substitute this back into the cost equation to get

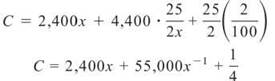
Take the derivative and do the wiggle thing:

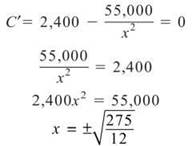
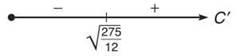
Only the positive answer makes sense (your box cannot have a negative length without ripping apart time and space, creating a black hole, and swallowing everyone within 2 light years in its diabolical gaping open top).

Therefore, the optimal value for * will be 4.787135539, which makes the optimal value for y

Therefore, the dimensions providing the lowest cost are 4.787 in x 2.611 in x 4 in. (By the way, the lowest cost will be nearly $23,000. Do you think I still need to buy a card?)