Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 6. Applications of the Derivative

TECHNOLOGY: MODELING A PARTICLES MOVEMENT WITH A GRAPHING CALCULATOR

The TI-83 includes a neat feature that allows you to view particle motion problems quite simply. If you are an AB student, you’ll need to delve into the world of parametric equations (just for a second, and it won’t hurt a bit—I promise). Although a lot of information can be gathered from a particle’s position equation, nothing beats seeing the particle running back and forth across the x-axis, working up particle sweat and checking its particle pulse. Let’s revisit Example 6 from our not-too-distant past to see how this works.

Example 11: If a particle moves along the x-axis according to position equation s(t) = t³ — 10t² + 25t, how many times does the particle change direction for t ≥ 0?

Solution: Switch your calculator to parametric mode. This is done by pressing [Mode], arrowing down to the “Par” option, and pressing [Enter], Notice that the “Y=” screen has changed; every equation now requires an x and a y component to graph. In the “_X1T =” line, type the position equation, pressing [x,t,0] for each variable. In the “Y_1T = ”line, type 0—this ensures that the particle will always have a height of 0 and never leave the x-axis. Finally, use the arrows to make your way to the little “\” symbol next to “X_1T” =. This chooses what the graph will look like. Pressing [Enter] twice on this symbol changes it to “—O”. Your calculator screen should look like the graphic below before you continue:

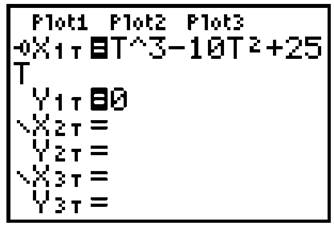
Now, press the [Window] button. Make sure your “Tmin” value is 0, since the problem requires that t ≥ 0. A good value for “Tmax” is 10. Now, press [Graph], The little particle should zip off to the right, turn around, and then move off to the right again—this time forever. Thus, it changed direction twice. If the particle moved off the screen, you can always increase the “Xmin” and “Xmax” values of the graph.

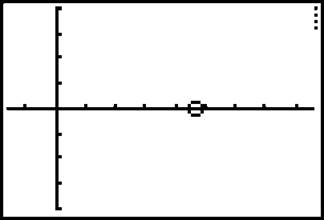
You may be wondering how mind-bogglingly useful this trick is in the grand scheme of things. The answer is “not very.” However, if you’ve had difficulty imagining the movement of a particle on a horizontal axis, this exercise can be very enlightening. If the particle is moving on the y-axis, reverse the values you typed, making the “X_1T” value 0 and the “Y_1T” the equation. If the particle’s movement is not restricted to a line, the process is even easier, as demonstrated in the next example.

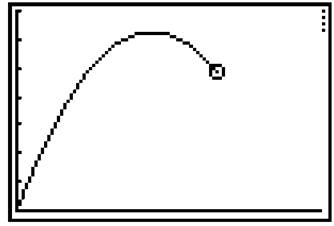
Example 12: Cleverly instruct your calculator to model the motion of a cannonball whose position equation is s(t) = —16t² + 20t.

Solution: Set your calculator back to “Func” mode by pressing the [Mode] button and type the above equation on the “Y=” screen. (This time, the variables will be x’s instead of fs, but that won’t affect the graph one bit.) Make sure to arrow over to the “\” symbol, and change it to a “—O”. Go ahead and [Graph] the equation. You may want to adjust the window a little bit. The graph below (with the cannonball in mid-air) has the following settings: Xmin = 0, Xmax = 1.5, Ymin = 0, Ymax = 7.

EXERCISE 8

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 7 THROUGH 12.

1. Draw the graph of a function, g, that satisfies the following conditions: g has domain [—5,8], g has relative minima at x = —3 and x = 4, g has relative maxima at x = —1 and x = 6, g has its absolute maximum at x = —5, and g’s absolute minimum occurs at x = 4.

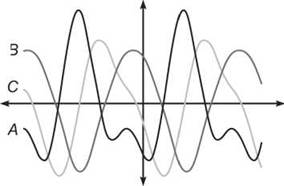
2. The graphs of h(x), h’(x), and h"(x) are given below. Determine which graph is which, and justify your answer.

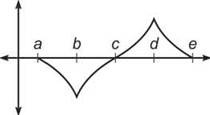
3. Draw the graph of f(x) based on the following chart of the signs of f’s derivatives, given that f is continuous, a < b < c < d < e, and f(a) = f(e) = 0. (Note: DNE means “does not exist.”)

4. Below is a graph of a car’s velocity. Answer the following questions based on the graph.

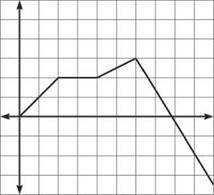
(a) On what intervals is the car moving forward?

(b) When is the car’s speed the greatest?

(c) When is the car decelerating?

5. A particle moves along the y-axis according to the continuous, differentiable curve s(t), which contains the values given in the table below.

What is the approximate velocity of the particle at t = 5?

6. Below is a graph of h"(x). Answer the following questions based on the graph.

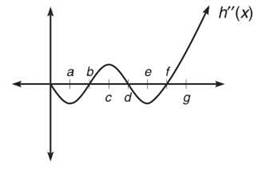
(a) On what intervals is h concave up?

(b) On what intervals is h' concave down?

(c) What are the inflection points of h'?

7. If a particle moves along the v-axis according to the position equation s(t) = t⁴ — 4t² + 3 (for t ≥ 0). If s is measured in feet and t in seconds, answer the following questions:

(a) What is the value of t guaranteed by the Mean Value Theorem for the interval [0,3]?

(b) What is the particle’s velocity and acceleration when t = 3?

(c) When is the particle moving forward?

8. (For fans of the movie Willie Wonka and the Chocolate Factory): Naughty children. No one will listen to Mr. Wonka’s instructions. Now Violet has gone and chewed the three-course-meal gum, and she’s begun to turn blue. In fact, she’s swelling to the size of a giant blueberry! If her torso swells such that her radius is increasing at a constant rate of 2 in/sec, at what rate is the surface area of her berry body increasing when her radius is 36 feet?

9. What is the volume of the largest right circular cylinder that can be inscribed in a sphere of radius 4 feet?

10. Two cars move on straight roads that are at a 50° angle to each other, as pictured below.

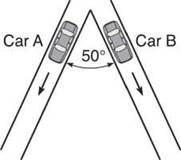
If car A moves at a constant rate of 40 mph, car B moves at a constant rate of 35 mph, and they started from the intersection at the same time, what is the rate of change of the distance between the cars once car A has traveled 25 miles? (Hint: the Law of Cosines)

*11. A particle moves along the path defined by x = cos t, y = sin 2t.

(a) Find the acceleration vector for the particle at t = 7π/6.

(b) When is the speed of the particle 1/2?

12. James’ Diabolical Challenge: You are contracted to build an animal cage for the Discovery Channel. One of the sides of the cage will be a river, with the remaining boundaries being constructed of fencing. You are given 400 feet of fence and are required to incorporate at least 100 feet of coastline. You can build either a rectangular fence or a semicircular one. Find the dimensions of the cage that give the greatest area, and justify your answer mathematically. ^*

*a BC-only problem

ANSWERS AND EXPLANATIONS

1. There are numerous possible solutions to this problem, but they all look very similar. Remember, relative extrema are little “hills and valleys” in the graph, and absolute extrema (guaranteed by the Extreme Value Theorem) are the highest and lowest points on a closed interval. Also, remember that absolute extrema must occur either at a relative extrema (like x = 4) or at an endpoint (like x = —5).

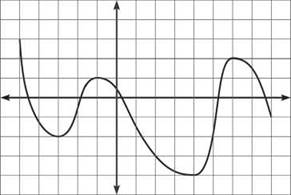
2. Graph B is h(x), graph C is h'(x), and graph A is h"(x). Notice that C has a value of 0 each time B has a relative extrema point. Furthermore, C is positive whenever B is increasing and negative when B is decreasing. Notice that A is negative whenever B is concave down and positive whenever B is concave up. (Therefore, A has a value of 0, or an x-intercept, each time B has an inflection point, and each time C has an extrema point.) You don’t need to apply every one of these connections—-just enough to differentiate (no pun intended) among the three.

3. Let’s take the interval a < x < b as an example. On that interval, both f'(x) and f"(x) are negative. Therefore, f(x) will be decreasing and concave down. There’s only one way to draw such a curve, and it looks like the following:

You know that/is continuous, but no derivative exists at x = b and x = d. As you draw the graph, you can tell that no derivative exists because both values of x result in a cusp. A correct graph looks something like the following:

4. (a) The car’s moving forward whenever its velocity is positive. We are given the graph of velocity, and it is positive on (0,8). The car’s velocity is clearly decreasing on (6,10), but the velocity is not negative until t > 8.

(b) Because speed is the absolute value of velocity, the direction of the car is irrelevant. Therefore, the speed of the car is greatest at t = 10. The speed there is a little more than 3, whereas the top speed the car reached while traveling forward was at t = 6, when the speed and velocity were both 3.

(c) Acceleration is based on the second derivative. The car will decelerate when the position function is concave down and when the velocity function is decreasing. Therefore, the car is decelerating on (6,10). This may confuse you, since the car is traveling its fastest at t = 10. The magnitude (absolute value) of the car’s acceleration there is actually pretty high, but the car still is traveling backward, so the acceleration is becoming more and more negative (technically decelerating).

5. The question is asking you to approximate s'(5). To do so, calculate the slope of the secant line connecting the points (3,9) and (5,11)—this is the best approximation we can use. Therefore, s'(5) ≈ 1.

6. (a) h is concave up whenever h" is positive, so the answer is (b,d) ∪ (f,∞).

(b) In order to determine the concavity of h', you need to move “down” two derivatives to h"' (since the signs of the second derivative of a function describe its concavity). You also know that the signs of h'" will describe the direction of h". The question is essentially asking you where h'" is negative, and that will happen wherever h" is decreasing. Therefore, the answer is (0,a) ∪ (c,e).

(c) The inflection points of h' occur whenever h'" equals 0 and the concavity actually changes (much like an extrema point is where the derivative equals 0 and the direction changes). You also know that h'" describes the direction of h". Therefore, whenever h" changes direction, h' will have an inflection point: x = a, x = c, and x = e.

7. (a) The Mean Value Theorem states that there exists some c on the interval such that

In other words, there exists a tangent line at some c that has the same slope as the secant line over the entire interval.

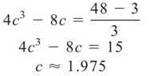
The velocity is the first derivative of position, and acceleration is the second:

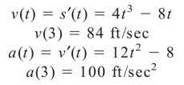
(c) The particle is moving forward whenever its first derivative is positive, so construct a wiggle graph for v:

v(t) = 4t³ - 8t = 0

4t(t² - 2) = 0

Critical numbers: t = 0, ±√2

According to the wiggle graph, the particle is moving forward on the interval (√2,∞). Don’t forget that the original problem stipulates t ≥ 0. Without that restriction, the answer would also have included (-√2,0).

8. This is a related rates problem. Begin with the formula for surface area of a sphere, and take the derivative with respect to time:

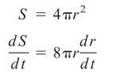
Now, plug in the given information to solve for dS/dt:

9. Your ultimate goal is to maximize the volume of a cylinder, so your primary equation should be the following formula:

V = πr²h

However, you have two variables, and it’s going to require some cleverness to eliminate one of them. Below is a diagram of our situation. On it is drawn a triangle, which connects the center of the sphere to the intersection point of the cylinder and sphere to a point on the cylinder at height h/2.

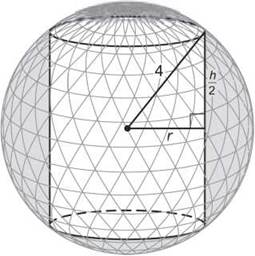
By the Pythagorean Theorem, you have

Solve this equation for r² to eliminate the r² in the primary equation:

Substitute this into the primary equation, and you can use the familiar methods to maximize the volume:

The wiggle graph verifies that 4.618802154 is the maximum height. The corresponding radius will be

so the maximum volume is V = πr²h ≈ 154.778 ft³.

10. The first question to be answered in this related rates dilemma is how much time has passed if the first car has traveled 25 miles. A simple proportion helps you to figure this out. If a car travels 40 miles in an hour (60 minutes), then how many minutes, m, does it require to travel 25 miles?

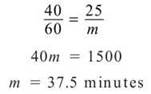
Now you can figure out how far car B has traveled using the same method:

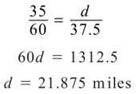
With all this fabulous information, you can construct the diagram below.

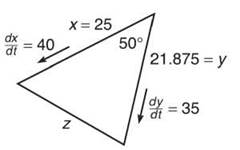
It is quite easy to figure out z using the Law of Cosines:

z² = 25² + 21.875² - 2(25)(21.875)cos 50

z = 20.01166352 miles

To tie this problem up into a nice bundle, you should use the Law of Cosines (since the triangle is oblique—not a right triangle) and derive with respect to t:

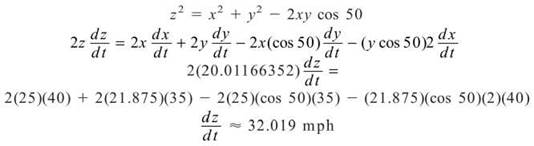
11. (a) The position vector is given by s = (cos t)i + (sin 2t)j. Take two derivatives to get the acceleration vector: a = (—cos t)i + (—4sin 2t)j. The acceleration vector at t = 7π/6 will be

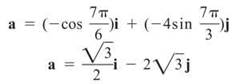
(b) First, find the velocity vector by taking the derivative of position:

v = (-sin t)i + (2cos 2t)j

The speed of the particle is given by the norm of the velocity vector, so set its norm equal to 1/2 and solve for t:

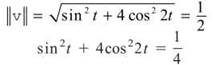
If you try to solve this equation by graphing, you’ll see that the graph never crosses the v-axis, so there are no solutions. The particle never travels at a speed of 1/2.

12. This problem asks you to find the maximum area, with the condition that a non-fenced coastline be used (ignore the 100 feet of coastline requirement for now). Below are the two cages whose area you want to maximize:

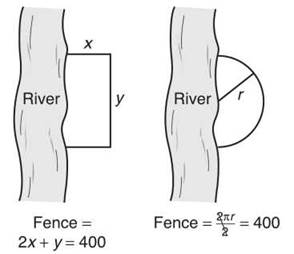
Here are the optimization problems, one at a time:

Rectangular cage:

You want to maximize area, so it is your primary equation:

A = xy

You also know that 2x + y = 400, so use that information to eliminate a variable by solving for x or y:

2x + y = 400

y = 400 - 2x

Now, substitute back into the area equation to find the maximum:

A = x(400 - 2x)

A = 400x - 2x²

A' = 400 - 4x = 0

x = 100

y = 400 - 2(100) = 200

Therefore, the maximum dimensions of the rectangular cage are 100 ft x 200 ft, for an area of 20,000 ft². (By the way, this meets the 100 ft coastline requirement without any trouble at all. See? I told you not to worry about it!)

Semicircular fence:

This problem does not require the process of optimization at all. If you know that the circumference of the semicircle is 400, then πr = 400 and r = 400/π. Therefore, the enclosed area will be

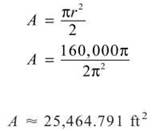
You should definitely go with the semicircular fence. You get more than 5,000 ft² extra space.

SUMMING IT UP

• If something is decreasing or becoming smaller, the rate of change will be negative.

• You can only insert a constant into your primary equation in related rates if that constant cannot change throughout the problem.

• Some students confuse the Mean Value Theorem with the Intermediate Value Theorem. They are similar only in that they are both existence theorems, in that they guarantee the existence of something.

• Two of the major characteristics used to describe graphs are direction and concavity.

• Optimization is the process of finding an optimal value, either maximum or minimum, under strict conditions. You may be asked to minimize area, maximize volume, minimize cost, or maximize profit, just to name a few applications.