Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 7. Integration

HANDS-ON ACTIVITY 7.2: ACCUMULATION FUNCTIONS

Accumulation functions are a new emphasis on the AP test. Not all books refer to them by this name, but the leaders in calculus reform have begun to use this terminology. Therefore, I will bend to peer pressure and use it as well. Accumulation functions are natural (and neato) extensions to definite integrals.

1. Given a function and the function g(t) defined by the graph

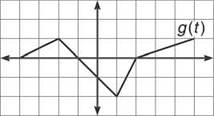
Evaluate f(1). Plug 1 into f(x), even though it may feel strange, and evaluate the definite integral.

_____________________________________________________

_____________________________________________________

2. How did the function f get its value?

_____________________________________________________

_____________________________________________________

3. Evaluate f(—1). Why is your answer positive?

_____________________________________________________

_____________________________________________________

4. For what integral value(s) of c does f(c) = —1? Complete the chart below to decide.

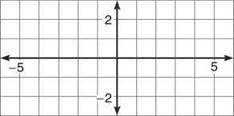
5. Based on the table you created in number 4, graph f(x).

6. Find f'(x), and justify your answer.

_____________________________________________________

_____________________________________________________

7. What relationship do you notice between f(x) and g(x), and why?

_____________________________________________________

_____________________________________________________

8. Evaluate f"(—3).

_____________________________________________________

_____________________________________________________

SOLUTIONS TO HANDS-ON ACTIVITY 7.2

1. In other words, f(1) is the area beneath g(t) on the interval [0,1]. That area is a small trapezoid with height 1 and bases of length 1 and 2. (You could also calculate the area as the sum of the square and triangle that make up the trapezoid.) Either way, the signed area is —3/2 (negative because it is below the x-axis).

2. f got its value from the amount of area “above” g(t) on the interval 0 to whatever the input was (in this case, 1). In other words, by accumulating signed area, f is an accumulation function.

3. Notice that the lower number is on top, which is weird, since it is usually on the bottom. Therefore, you should change it so that the lower limit of integration is on the bottom, but remember that doing so makes the definite integral its opposite, since

The triangle between —1 and 0 is below the v-axis, so it should have area —1/2 so the integral equals:

4. Use geometric formulas to calculate the areas. Don’t forget that which is all of the accumulated area from x = 0 to x = 4. The area from x = 0 to x = 1 is —3/2, as we’ve said. The area from x = 1 to x = 2 is a right triangle of area —1. The area from x = 2 to x = 4 is a right triangle with base 2 and height 2/3 (since the slope of the line from x = 2 to x = 5 is 1/3). Therefore, all of the accumulated area from x = 0 to x = 4 is

The correct answers are c = —4 and 5.

5.

6. according to Fundamental Theorem Part Two. Don’t miss the importance of this: the graph of f’(x) is the graph you were given in the first place, g(t). (The fact that there’s a t instead of an x makes no difference in the graph, but you should use g(x) to keep your notation consistent.)

7. The graph of g(x) acts like any first derivative graph. g(x) is positive when f(x) is increasing (look at the interval (-4,-1) on each). g(x) is 0 whenever f(x) has a relative extrema point (look at x = —1 and —2).

8. f"(—3) is the slope of the tangent line to f'(x) at x = —3. Since g(x) is f'(x), you are trying to find the slope of the tangent line to g(x) at x = —3. Luckily, g(x) is linear at x = —3, and the slope of the line segment is 1/2. Remember, the slope of a tangent line to a linear graph is simply the slope of that linear graph. Therefore, f"(—3) = 1/2.

EXERCISE 5

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

DO NOT USE A GRAPHING CALCULATOR FOR ANY OF THESE PROBLEMS.

1. If why is/not an accumulation function?

2. One famous function gets its value by accumulating area beneath the graph of y = 1/x.

(a) If we call the famous function f(x) and define it as find f(2).

(b) What is the name of the famous function?

(c) Evaluate f(10), and verify that the result matches the output of the famous function.

3. If evaluate g(3π), g'(3π), and g"(3π).

4. If h(t) is defined by the below graph and

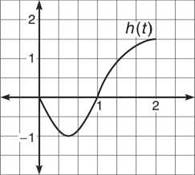
(a) Approximate m(3/2).

(b) Evaluate m’(2).

(c) Describe the concavity of m(x) for [0,2].

(d) Write the following function values in order from least to greatest: m(1/2), m(1) and m(2).

ANSWERS AND EXPLANATIONS

1. An accumulation function has an x in its limits of integration.

2. (a) You know that the integral of 1/t is ln |t| , so you get

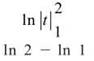
and since ln 1 = 0, the answer is In 2. Notice, f(2) = ln 2.

(b) The name of this famous function is the natural logarithm! f(x) = ln x. It makes sense since f’(x) = 1/x.

(c) So,

f(10) = ln 10 - ln 1 = ln 10

This works every time, since the lower limit of integration is always 1 and ln 1 is 0.

3. Let’s do one at a time and start with g(3π).

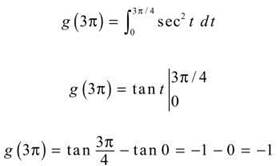
According to Fundamental Theorem Part Two, (Don’t forget to multiply by the derivative of the upper limit of integration, which is 1/4.) Therefore,

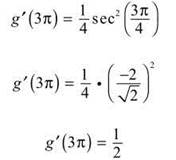
Finally, use the Chain Rule to find g"(x):

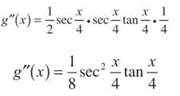
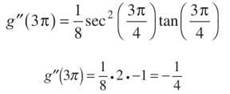
NOTE. Counting boxes to approximate area may feel inaccurate, but it’s often more accurate than Riemann sums and, since you’d be approximating function values to use the Trapezoidal Rule in this case anyway, why bother? Sure it’s a guess, but the directions do say approximate.

4. (a) Because there is no function, you cannot find this exact area. However, you do know that the area from x = 1/2 to x = 1 is negative, and the area from x = 1 to x = 3/2 is positive. You could use Riemann sums or the Trapezoidal Rule to approximate; however, these methods are mostly used when you happen to know the function. Since there is no function, why not make it a total approximation and count boxes of area? Each box on the graph of the function is one square unit. Therefore, the negative area is approximately — 1.9 (your answer may be different but should be relatively close), and the positive area should be 2.

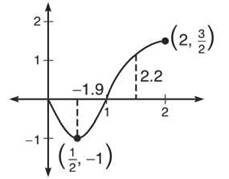
Therefore, m(3/2) ≈ 0.3

(b) According to Fundamental Theorem Part Two, m'(x) = h(x). Therefore, m’(2) = h(2) = 3/2, according to its graph.

(c) The concavity of m(x) is described by the signs of m"(x). In addition, m"(x)’s signs describe the direction of m'(x), or h(x). Therefore, whenever h(x) is increasing, m"(x) will be positive and vice versa. To summarize, m(x) will be concave up whenever h(x) is increasing: (1/2,2), and m(x) will be concave down wherever h(x) is decreasing: (0,1/2).

(d) Using the method of counting boxes, we have already determined that m(1) ≈ —1.9. We also said that m(3/2) ≈ .3, so it makes sense to say that m(2) > m(3/2), since m accumulates a lot of additional positive area from x = 3/2 to x = 2. Therefore, we know that m(2) is positive (if you count boxes, m(2) ≈ 4). Finally, m(1/2) is 0, since (according to a property of definite integrals). With all this in mind, we know that m(1) < m(1/2) < m(2).