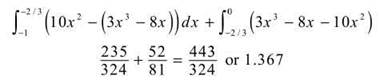Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 9. Applications of Integration

OVERVIEW

• Hands-On Activity 9.1: Area between curves

• The disk and washer methods

• The shell method

• Finding the volume of regions with known cross sections

• Arc length (BC topic only)

• Polar area (BC topic only)

• Technology: Using your calculator efficiently

• Summing it up

Learning how to integrate, although a fun adventure in and of itself (yeah right), is just the beginning. Just as derivatives had keen applications such as related rates and optimization, integrating has its own applications, which are primarily concerned with finding area and volume generated by graphs. These topics always remind me of one thing—getting close to the AP test! Although BC students have an extra chapter (and what a fun chapter that is), AB students are nearing the home stretch for the AP test. Don’t give up, and keep your focus—you’re almost done.

HANDS-ON ACTIVITY 9.1: AREA BETWEEN CURVES

You can already find the area between a curve and the x-axis (thanks to the Fundamental Theorem). Now, you will learn how to find the area between any two integrable curves. I can tell that you’re excited. Let’s get right to it.

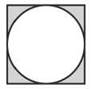
1. If a circle is inscribed in a square whose side length is 9, find the area of the shaded region.

__________________________________________________

__________________________________________________

2. Describe the technique you used to complete problem 1.

__________________________________________________

__________________________________________________

3. Below are the graphs of y = 4 and y = x² in the first quadrant. Where do these two graphs intersect?

__________________________________________________

4. Evaluate the definite integrals and Using those two integrals, how can you find the shaded area? (Use a technique similar to the circle and square problem from number 1.)

__________________________________________________

__________________________________________________

__________________________________________________

NOTE. The fact that some of the area is below the x-axis will not matter. The area between curves will always be positive—it is not signed area. If you get a negative answer, you subtracted in the wrong order.

5. Fill in the blanks below to complete the statement:

When finding the area enclosed by two curves that contain x variables, you are adding the sum of the areas of an infinite number of vertical __________s. In practice, you subtract the definite integral of the __________ from the definite integral of the __________. The limits of integration for those integrals should be the x-values of the __________.

6. Graph the curves y = 2 — x² and y = x² — 3. Lightly shade the total area between the curves (not just in the first quadrant this time). Set up the integral that represents the area, but do not integrate it.

__________________________________________________

__________________________________________________

7. If your functions both contain y’s, how will your technique for finding the area between them differ?

__________________________________________________

__________________________________________________

8. Fill in the blanks below to complete the statement:

When finding the area enclosed by two curves that contain y variables, you are adding the sum of the areas of an infinite number of __________. In practice, you subtract the definite integral of the __________ from the definite integral of the __________. The limits of integration for those integrals should be the __________.

9. Find the area in the first quadrant enclosed by the curves x = y² and x = √y.

__________________________________________________

__________________________________________________

SELECTED SOLUTIONS TO HANDS-ON ACTIVITY 9.1

1. The radius of the circle must be 9/2 since its diameter is the same as the side of the square. The shaded area is

2. You find the area of the square and subtract the area of the circle.

3. You can find this answer by setting them equal to one another.

x² = 4

x = ±2

They intersect at the point (2,4).

4. and as shown in the following diagrams.

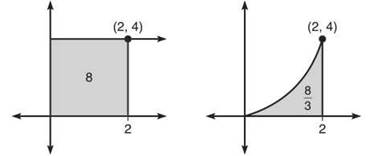
Notice that the left area minus the right area equals the shaded area in the problem. Therefore, the answer is

5. When finding the area enclosed by two curves that contain v variables, you are adding the sum of the areas of an infinite number of vertical rectangles. In practice, you subtract the definite integral of the lower curve from the definite integral of the higher curve. The limits of integration for those integrals should be the .x-values of the intersection points.

6.

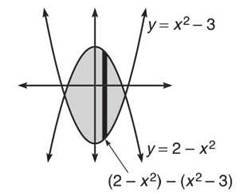
The diagram contains a single, dark vertical rectangle, which is one of the infinite number of rectangles that make up the shaded area. This makes it easy to see that you will integrate the top curve minus the bottom curve, or (2 — x²) — (x² — 3), as that is the length of the rectangle.

Find the intersection values by setting the functions equal.

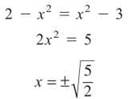
Therefore, the area is given by

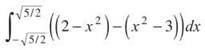
7. When functions contain y’s instead of x’s, the rightmost function is the greater instead of the higher function. Also, you would use the y-coordinate of the intersection point rather than the x-coordinate.

8. horizontal rectangles, leftmost curve, rightmost curve, y-coordinates of the points of intersection.

9.

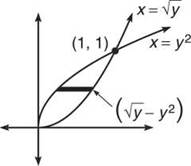
TIP. If you have problems drawing functions of y, plot points to construct the graph.

Because these functions both contain y’s, you are using horizontal rectangles of length (right — left) = √y — y². The functions intersect at (1,1) and (0,0). Don’t forget that you have to use the y-coordinate (even though it’s the same as the x in this case).

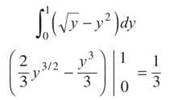
EXERCISE 1

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

DO NOT USE A GRAPHING CALCULATOR FOR PROBLEMS 1 AND 4.

TIP. Remember that vertical rectangles relate to x variables and horizontal rectangles relate to y variables. This will help you immensely in the next section.

1. Calculate the area bounded by f(x) = x⁵ — 5x³ and the x-axis. What important conclusion can be drawn from this problem?

2. Calculate the area bounded by y = x³ — 4x and y = (x + 2)² in the second quadrant.

3. Calculate the area in the first quadrant bounded by x = 5 and y = x² + 2 twice—once with horizontal rectangles and once with vertical ones.

4. Calculate the area bounded by x = y + 4y — 5 and y = —1/2x + 1.

5. Calculate the area bounded by y = 3x³ — 8x, y = 10x², x = 0, and x = —1.

ANSWERS AND EXPLANATIONS

1. First, you need to find the points of intersection of the graphs by setting them equal.

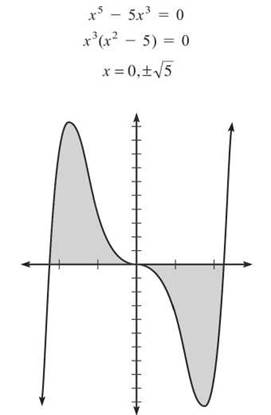
This problem must be split into two separate integrals. On [-√5,0], f(x) is the “top” function, whereas on [0,-√5], the x-axis (y = 0) is the “top” function. However, you only need to calculate one of these regions since f(x) is odd and therefore origin-symmetric (both of the regions will have the same area).

We will calculate the area of the region on [0,-√5]. Don’t forget that y = 0 is the “top” function.

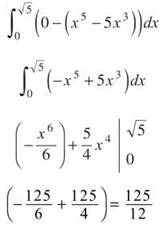
Therefore, the entire region between the two curves is The important conclusion to be drawn? The Fundamental Theorem of Calculus is just an extension of this method. (Before, our unstated lower curve was always 0, since upper curve — 0 = upper curve.)

2. These are both functions of x, so you use x-boundaries and integrate top — bottom . (You also use vertical rectangles with x functions.) Graph them to see which is which.

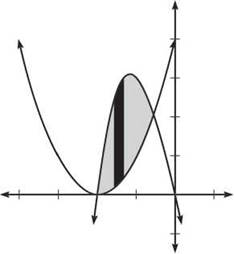
The top function is x³ — 4x. Now, find the intersection points of the graphs.

x³ — 4x = x² + 4x + 4

x³ — x² — 8x — 4 = 0

Solve this equation using your calculator to get x = —2 and —.5615528128 (the other solution corresponds to an intersection point in the first quadrant). The area will be

The area is approximately 2.402 square units.

3. Using vertical rectangles is much easier in this problem, although both give you the same solution.

Vertical rectangles (using x‘s):

The area of the region is found using the Fundamental Theorem.

NOTE. Remember, you should use right-left with horizontal rectangles, and the limits of integration are y’s.

Horizontal rectangles (using y’s):

From y = 0 to y = 2, the right-hand function is x = 5, and the left-hand function is x = 0. In fact, that area is simply a rectangle of area 10.

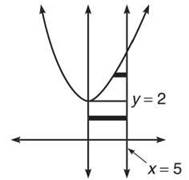
How do you find that upper intersection point? You cannot just set the equations equal, because one is an equation in terms of x. If you want to use horizontal rectangles, you have to go whole hog and change everything to y’s.

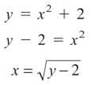
Now you can set the two equal to find the boundaries.

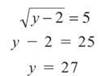
NOTE. The reason we had to split the problem into two integrals was the change of bound a ries at y = 2. With vertical rectangles, the bound a ries stayed the same the whole time. That’s why it was easier.

The intersection point is (5,27). Notice that the horizontal rectangles from y = 2 to y = 27 have a right-hand boundary of x = 5 and a left-hand boundary of . Since we already know the lower rectangular area is 10, let’s find the other area.

The total area is and the answer matches our vertical rectangle answer.

4. You have to use horizontal rectangles here. One of the functions is in terms of y, and there is no changing that one into terms of x easily. Therefore, you need to change the other and put it in terms of y also.

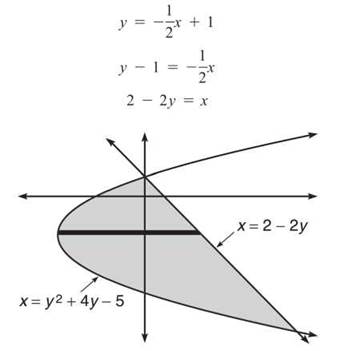
The intersection points will be

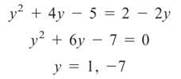
On the entire interval from y = 1 to y = —7, the line forms the right-hand boundary, so the area between the curves will be

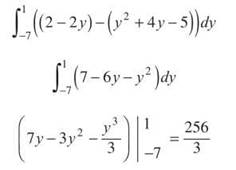
5. Both of these functions are in terms of x, so you should use vertical rectangles and v boundaries for integration.

This graph is stretched to feature the area in question.

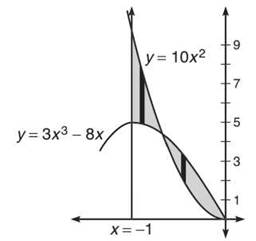
These graphs intersect in the interval [—1,0]. Find that point.

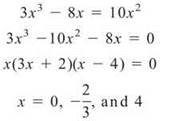
Clearly, —2/3 is the value we need. However, we will need two separate integrals. On the interval [—1,—2/3], the quadratic function is on top. However, on [—2/3,0], the cubic function is on top. Therefore, the total area is