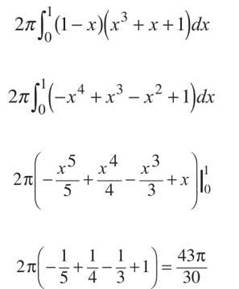Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 9. Applications of Integration
THE SHELL METHOD
NOTE. There are no places on the AP test in which you have to apply the Shell Method, according to the College Board. However, the Shell Method can save you time, so it’s good to know.
I must confess: I really don’t like baseball all that much. I used to love playing baseball, but watching it on television (or even in the stadium, I am sad to say) just doesn’t cut it for me. A bunch of guys standing around in tight pants sounds like Broadway musical tryouts. At least in football, the guys in tight pants are trying to hurt one another, so we can forgive the “nothing left to the imagination” attire.
One of the more interesting pieces of minutiae in baseball (which is far from trivial to the avid fan) is the designated hitter rule. You see, the American League allows coaches to replace the pitchers (who are generally very poor batters) with other players, whose only job is to hit for the pitcher in the lineup. It’s a good concept: allow one person good at something to stand in for someone else.
The Shell Method is the designated hitter for calculus, and there’s no debate about whether or not it is good for baseball. When the Disk or Washer Method is hard (or even impossible) to use, the Shell Method steps in and hits one out of the park. The Shell Method doesn’t even care if the rotational solid has a hole in it or not (whereas that scares the Disk Method off). The Shell Method uses rectangles that are parallel to the rotational axis, so it can even save you time with variable conversions. The rule itself is a little bizarre, though. I find it difficult to visualize, so spend more time on memorizing and applying it than trying to figure out its place in the cosmos.
The Shell Method: If a region is rotated about a horizontal or vertical axis on an interval [a,b], the resulting volume is given by
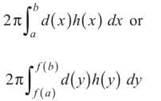
Now, you probably see why I call this the Designated Hitter; it helps you memorize the formula. But what do the two functions stand for?
d(x) is the distance from the rotational axis to a rectangle in the region.
h(x) is the height of that rectangle.
TIP. Remember, in the Shell Method, the rectangles will be parallel to the rotational axis.
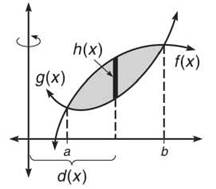
Example 4: Consider the following region, bounded by functions f(x) and g(x), that intersect at x = a and x = b. What is the volume of this region if rotated about the y-axis?
NOTE. You do not have to adjust the Shell Method at all if the rotational solid has a hole in it. The method remains exactly the same.
Solution: The key to the Shell Method is drawing the darkened rectangle in the region (which is parallel to the rotational axis). The function d(x) represents how far that rectangle is from the y-axis. We could have drawn that rectangle anywhere on the interval, and we can’t be sure exactly where it is, so we will say that it is a distance of v away. Thus, d(x) = x. Secondly, what is the height of that rectangle? You find it the same way you have all chapter: top — bottom. This is how h(x) gets its value, so h(x) = f(x) — g(x). Therefore, the volume of the indicated region is
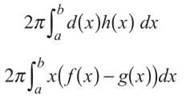
Sometimes, students are confused about how to find d(x). It’s not complicated, so don’t get frustrated. Think about it this way: If you are given the graph below and asked to give the coordinates of the point, how would you respond?
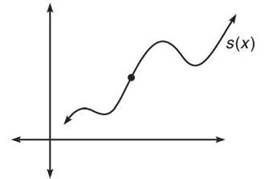
The only correct response would be very generic: (x,s(x)). In this instance, you assign an unknown horizontal distance a value of x. That’s all you’re doing with the Shell Method. However, d(x) is not always just x (or y), as you’ll see in the next example.
Example 5: What volume results if you rotate the region in the first quadrant bounded by y = x2 + 1, x = 1, and y = 1 about the line y = 1/2?
NOTE. You can use the Washer Method to solve Example 5, but we’ll use the Shell Method, since that’s the name of this section.
Solution: To begin, breathe deeply, and draw the region. Then, draw a dark rectangle in the region parallel to the rotational axis.
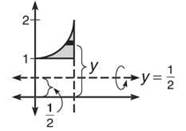
All of the rectangles are horizontal now, so all of the equations must be in terms of y. Therefore, you must rewrite y = x2 + 1 as 
How far is that darkened rectangle from the x-axis? Because you don’t know exactly, you must say that it is y units away. However, that’s not d(y). To find it, we need to know how far the rectangle is from the rotational axis. Because the rectangle is y units above the x-axis and the rotational axis is 1/2 unit above the x-axis, d(y) = y — 1/2. This is much easier to visualize than to explain; look at the graph above for help. All you have left to do is to determine the value of h(y), the height (or length) of the rectangle. Its length is given by right — left and is 
Therefore, the volume will be
You can multiply this out and integrate each separately, but let’s embrace calculator technology for the time being. The answer is approximately 1.676.
This is the same answer you get using the Washer Method. If you don’t believe me, I’ll show you. The outer radius will be R(x) = (x2 + 1) — 1/2, and the inner radius is r(x) = 1/2. Therefore, the volume is
EXERCISE 3
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY NOT USE A GRAPHING CALCULATOR FOR THESE PROBLEMS
1. Find the volume generated by rotating the area in the first quadrant bounded by y = x2 and x = 2 about the line x = —2. Use the Shell Method.
2. Find the volume generated by rotating the area bounded by 
and y = 2 about the x-axis. Use the most appropriate method.
3. Find the volume generated by rotating the area bounded by y = √x, x = 4, and y = 0 about the line y = —3 using the
(a) Shell Method.
(b) Washer Method.
4. Find the volume generated by rotating the area bounded by y = x3 + x + 1, y = 0, and x = 1 about the line x = 1, and explain why the Shell Method must be used.
ANSWERS AND EXPLANATIONS
1. First, graph the region and draw your rectangle.
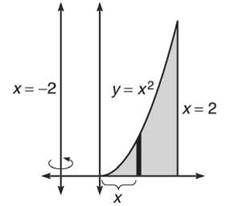
In this case, d(x) is more than just x; in fact, it is exactly two units more, so d(x) = x + 2. Even easier, h(x) = x2. Therefore, the volume is
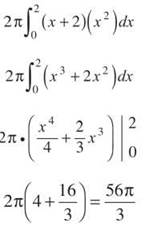
2. The Shell Method is not your best bet in this problem. You’d have to use horizontal rectangles, so the function would have to be put in terms of v, and the problem would only get more complicated from there.
Because the rotational solid will have a hole, you’ll need to use the Washer Method (which requires perpendicular rectangles; in this case, x’s). First, you need to find the intersection points of the graphs.
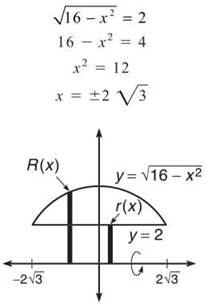
and r(x) = 2; therefore, the volume is
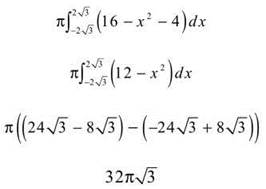
3. (a) The Shell Method will use horizontal rectangles and requires that you rewrite y = √x as x = y2.
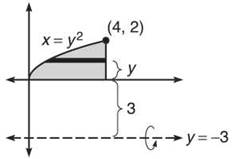
Based on the diagram, d(y) = y + 3 and h(y) = 4 — y2. Therefore, the volume is
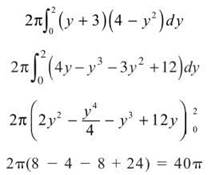
(b) The Washer Method uses vertical rectangles and the function in terms of x.
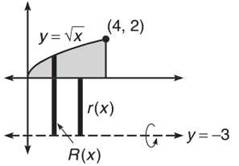
The outer radius is R(x) = √x — (—3) and the inner radius is r(x) = 0 — (—3). Therefore, the volume is
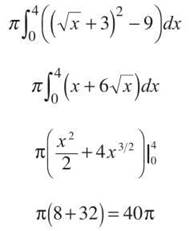
4. Even though the solid of revolution will have no hole in it, you cannot use the Disk Method. To do so, you would have to use horizontal rectangles and put the y = x3 + x + 1 in terms of y, which is impossible (you cannot solve that equation for x). Therefore, the Shell Method is the only way to go (since that requires vertical rectangles).
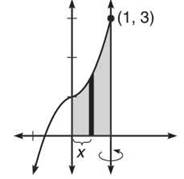
The distance from the axis of revolution to the rectangle in the region is 1 — x, and the height of the rectangle is x3 + x + 1. So, the volume generated will be
