Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 9. Applications of Integration
TECHNOLOGY: USING YOUR CALCULATOR EFFICIENTLY
By now, you know the four major calculator proficiencies you need for the AP test: graphing, finding roots (solving equations), evaluating numeric derivatives, and evaluating definite integrals. However, you may not be using all of the calculator’s features. Remember, the AP test is a high-stress situation and is governed by strict time constraints—you want the calculator to do as much as possible for you.
Take, for instance, problem 5 from the last problem set. (Even though it is a BC problem, the skills apply to AB students as well.) You should be using your calculator to serve two major purposes: finding the point of intersection and then evaluating three definite integrals. You already know how to find the solutions to the equation
3 — 2sin θ — 4cos θ = 0
but here’s a good tip. Once you find a root, press [Clear] twice to return to the home screen (you can also use [2nd] → [Mode], which is the [Quit] button). If you press [X,T,θ] and [Enter], the calculator gives you the root and shows more decimal places than it did on the graph screen. Now press [Sto→] and then [Alpha] → [Math] (the [A] button).
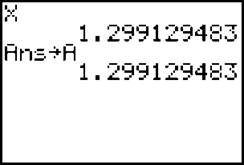
This stores that root as the variable A in the calculator’s memory; this way, any time you need that number, you can simply use A instead of typing it out. Follow the process again, and store the other root to B.
Now, let’s shorten the process of constantly typing the equations in as we find definite integrals. If you haven’t already, switch to polar mode and graph the two equations: r1 = 3 — 2sin θ and r2 = 4cos θ. Look how much easier it is to evaluate the second, troublesome integral from that problem when you use calculator shortcuts:
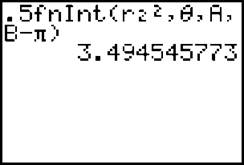
Instead of typing the limits of integration, just use the variables we defined. Instead of typing (4cos θ)2, just use r22. Once you type an equation into the “Y=” (or “r=”) screen, you can access those equations by pressing [Vars] → “Y-vars”. To get r2, you then select “Polar...” → “r2”. If you are an AB student, you will use only the “Y=” screen, and all these equations are found under [Vars] → “Y-vars” → “Function...”.
Look how much time you save when calculating the final integral if you employ all these shortcuts:
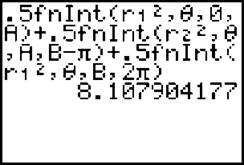
These methods help eliminate the errors of mistyping and help you concentrate on the business at hand—passing that AP test.
EXERCISE 7
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 4 THROUGH 6.
1. If region A is bounded by y = 3/x and y = — x + 4, find
(a) the area of A.
(b) the volume generated when A is rotated about the y-axis using both the Washer and Shell Methods.
(c) the volume of the solid with base A that has isosceles right triangular cross sections with hypotenuses perpendicular to the x-axis.
2. Prove that the volume of a sphere with radius r is 4/3πr3.
3. If region B is bounded by y = —√x + 2 and y = 1, find
(a) the area of B.
(b) the volume generated by rotating B about the y-axis.
(c) the volume generated when B is rotated about the line y = —1 using both the Washer and Shell Methods.
*4. If region C is bounded by the polar curve r = sin θ cos θ, find
(a) the area of C.
(b) the perimeter of C.
*5. Find the perimeter of the region bounded by x = y2 — y — 2 and the y-axis.
6. James’ Diabolical Challenge: A machine part is made from an alloy that costs $130 per cm3. The base of the part is bounded by the area between the functions y = x and y = x2 (x is measured in cm). The part can be made using either semicircular or equilateral triangular cross sections (perpendicular to the x-axis). Which method is less expensive?
*a BC-only question
ANSWERS AND EXPLANATIONS
1. (a) The area is the definite integral of top — bottom with x-boundaries reflecting their intersection.
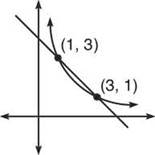
The area will be
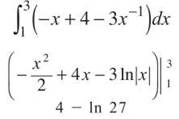
(b) Shell Method: Because you are rotating about a vertical axis, you use vertical rectangles with the Shell Method. No variables need to be converted—you use x’s.
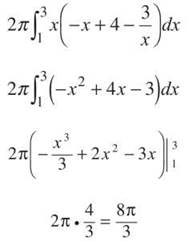
Washer Method: You need to convert the equations so that they are in terms of y: x = 4 — y, x = 3/y. The boundaries of integration are now the y-boundaries of the intersection, which are exactly the same as the x’s. The outer radius will be R(x) = (4 — y), and the inner radius is r(x) = 3/y.
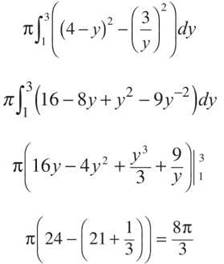
(c) In the problem set for known cross sections, we found that the area of an isosceles right triangle is h2/4, if h is the hypotenuse. The length of each hypotenuse will be h = —x + 4 — 3x-1. Therefore, the volume is
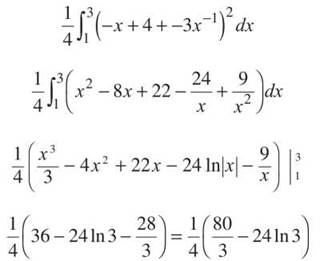
2. To create a sphere of your very own, you need to rotate a semicircle. A circle centered at the origin has equation x2 + y2 = r2. Solving for y gives you a semicircle equation of 
When rotated about the x-axis, this graph produces a sphere.
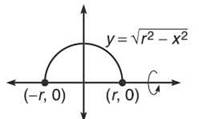
Use the Disk Method to find the volume.
Remember that r is a constant, so treat it as you would any number as you complete the problem.
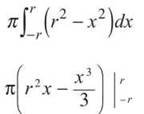
Now, plug r and —r into the expression in place of x (just as you have always done with the Fundamental Theorem).
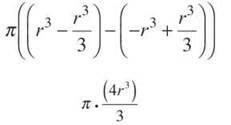
3. (a) The area is top — bottom with x-boundary limits.
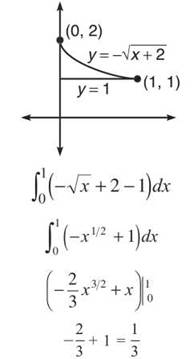
(b) There is no hole in the rotational solid, so you can use the Disk Method. To do so, however, you have to put everything in terms ofy, since the Disk Method requires horizontal rectangles in this case. (You can use the Shell Method, and you will get the same thing.)
Now that the equation is in terms of y, use y boundaries and complete the integration to find volume.
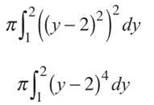
Set u = y — 2, and this is a simple u-substitution problem.
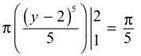
(c) Shell Method: You must use horizontal rectangles (since they are parallel to y = —1), and everything must be in terms of y.
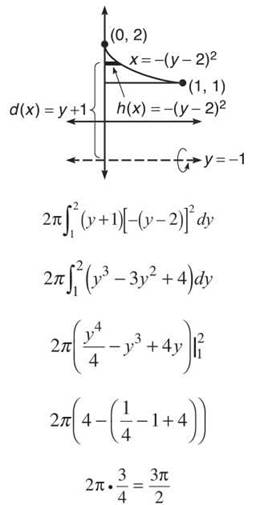
Washer Method: The washers will be in terms of x (since horizontal rectangles are perpendicular to the vertical axis of rotation).
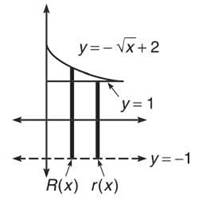
The outer radius is R(x) = —√x + 3, and the inner radius is r(x) = 2.
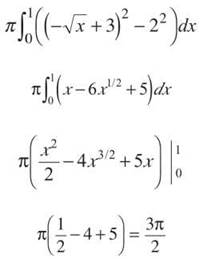
4. (a) This graph has four distinct petals that are framed by radial lines θ = 0, θ = π/2, θ = π, θ = 3π/2, and θ = 2π.
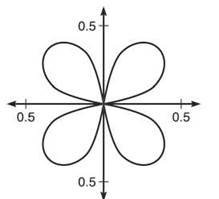
Because of the graph’s symmetry, we can find the area of the petal in the first quadrant and multiply it by 4.
The area of the single petal is .0981747704, so the total area is approximately .393.
(b) When finding the perimeter of the region, you are technically finding the arc length of its bounding function. To find polar arc length, you must first convert to parametric form by using x = r cos θ and y = r sin θ:
x = cos2θ sin 0, y = sin2θ cos θ
Now, take the derivative of each with respect to the parameter (which is θ instead of t in this problem.)
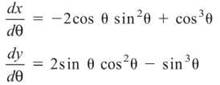
Now, plug these both into the formula
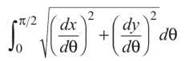
You’re crazy if you don’t use your calculator. Type it in very carefully. Here’s what it should look like:
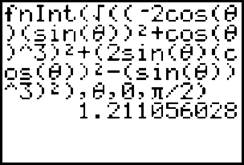
The total perimeter is four times that answer, which is approximately 4.844.
5. Again, you find the perimeter by calculating the arc length of the boundaries.
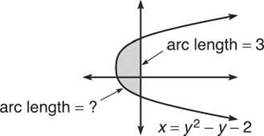
To find the length of the left boundary, you have to use the formula
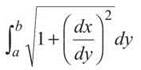
The derivative (with respect toy, since the expression is in terms of y) is x’ = 2y — 1. Therefore, the arc length is
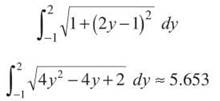
Therefore, the total perimeter is 5.653 + 3 = 8.653.
6. Begin by drawing the bounded region and a darkened rectangle on it perpendicular to the x-axis.
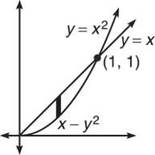
The length of the rectangle is x — x2, and the region has v-boundaries 0 and 1. Use this information to find the cross-sectional volumes separately.
Semicircle cross sections
The area of a semicircle is πr2/2 , and the dark rectangle would represent a diameter of the semicircle. Therefore, 
would be its radius. Now, integrate the formula for the area of a semicircle, substituting in the radius.
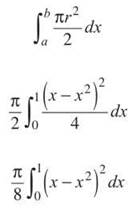
The volume is .0130899694, so the cost of the part would be approximately $1.70.
Equilateral triangle cross sections
The area of an equilateral triangle is 
so the volume of this machine part will be
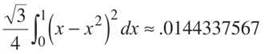
The resultant cost for the part is $1.87. Therefore, the part with the semicircle cross sections is cheaper.
SUMMING IT UP
• Just as derivatives have applications such as related rates and optimization, integrating has its own application, which is primarily concerned with finding area and volume generated by graphs.
• Remember, in the Shell Method, the rectangles will be parallel to the rotational axis.
• The best method to use in rotational solid volumes is one that requires the least amount of conversion.
• The four major calculator proficiencies you need for the test are
• Graphing
• Finding roots (solving equations)
• Evaluating numeric derivatives
• Evaluating definite integrals