Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 11. Sequences and Series (BC Topics Only)

CONVERGENCE TESTS FOR INFINITE SERIES

Your major focus in infinite series will be in determining whether or not the series converge; in some rare instances, you will also be able to provide the sum at which the series converge. Each of these tests works best for certain kinds of series, so make sure to learn the series characteristics that indicate which tests to use as well as how to apply the tests themselves. So, don’t just learn one or two and expect to be able to apply them in all situations; you need to know them all. I know, no rest for the wicked....

Geometric Series

TIP. Just as promised, the first term of the expansion is the a term of the geometric series.

Geometric series have the easiest test for convergence of them all, but first you need to know what a geometric series is. Every geometric series has the form

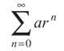
where a is a constant that can be factored out of each term and r is the ratio, the identical portion of each term raised to an increasing power as the terms increase. The major difference between this series and most other infinite series is that geometric series begin with n = 0 and not n = 1. However, that makes the a term very easy to find; the a term will be the first term in the geometric series when expanded, since it is multiplied by r⁰, which is just 1. Let’s expand the geometric series 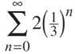to get a feel for these puppies:

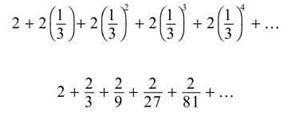
Not only will you be able to tell if this series actually adds up to something (converges), but we can actually find out exactly what the sum of the series is.

Geometric Series: The geometric series will diverge for |r| ≥ 1. It will only converge if 0 < |r|< 1. If the series does converge, it will converge to the sum Therefore, the series converges since the ratio, 1/3, is between 0 and 1. Furthermore, the sum of the series will be

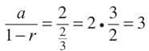
Example 4: Determine whether or not the following series converge; if they do, find the sum of the series.

(a)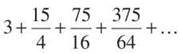

The first term is a, so a = 3. You also know that each term of the series contains a, so factor it out to determine r:

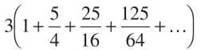
So, the n = 0 term is 1, the n = 1 term is 5/4, and the n = 2 term is 25/16. The numerators are powers of 5, and the denominators are powers of 4. This is just the series 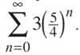However, 5/4 ≥ 1, so the series diverges. n=0

(b)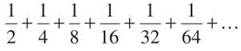

Recognize this problem? We have already decided that the answer must be 1, so let’s finally prove it. First of all, a = 1/2, so factor that out of everything:

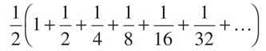
The ratio is definitely (1/2), making the series Therefore, the sum will be

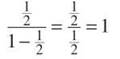
just as we thought it would be.

(c)

NOTE. Dividing the other terms by 1/4 is the same as multiplying them by 4.

Again, since a is the first term, 1/4, divide it out of all the other terms.

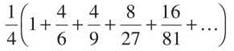
The 4/6 term can be reduced to 2/3, and the series in parentheses has ratio 2/3. Thus, the series converges (since 2/3 is between 0 and 1), and it has sum

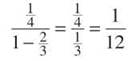
The Integral Test and P-Series

To help you remember the necessary conditions that must exist in order to apply the integral test, memorize the following phrase: In prison, dogs curse. The mneumonic device reinforces that in order to apply the Integral Test, the function must be positive, decreasing, and continuous. In essence, the Integral Test shows that an infinite series and an integral with an infinite upper bound have a lot in common: either they will both converge or both diverge.

The Integral Test: If a_n = f(n) is a positive, decreasing, continuous function, then and either both converge or both diverge. As an example, consider the harmonic series. We already know that the sequence converges, but does the infinite series converge? According to the Integral Test, it will if the integral does. Therefore, try to evaluate this improper integral:

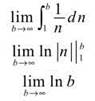
NOTE. It makes sense that p must be positive. If p = -2, that creates the series which definitely has an infinite height as x approaches infinity.

As x approaches infinity, ln x will approach a height of infinity; the graph has no horizontal asymptote or limiting value and will increase forever (although more slowly than many other graphs). Therefore, the integral diverges, and the infinite series must diverge, too.

The justification for the Integral Test lies in geometry. Remember that an integral is really the sum of an infinite number of rectangle areas; the above series was an infinite sum of numbers. If a function creates rectangles whose areas grow and result in divergence, then that same function will create outputs whose sums grow too much and also create divergence.

This leads us back to a brief discussion we began in the Improper Integrals section of Chapter 8. At that time, we discussed the set of improper integrals of the form We said that this integral will diverge for any p ≤ 1 but will converge for p > 1. We can now apply this fact to infinite series.

NOTE. The fact that I have not peppered this discussion on p-series with low-brow humor is a testament to my self-control.

P-series: A p-series is a series of the form 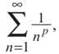where p is a positive number. A p-series will converge if p > 1 but will diverge if p ≤ 1. In the case of the harmonic series 1/n, p = 1, so it will diverge; you don’t have to apply the Integral Test as we did above, but if you do, it will become very clear exactly why the harmonic series diverges.

Example 5: Determine whether or not the following series converge, and explain how you arrived at your answer:

(a)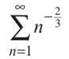

If you rewrite the series as 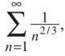it is a p-series with p = 3/2. Since 2/3 ≤ 1, the series will diverge.

(b)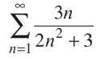

According to the Integral Test, the convergence of this series is correlated with the convergence of the related improper integral. Therefore, try to integrate:

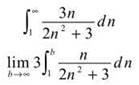
You should use u-substitution, with u = 2n² + 3. Don’t forget to replace 1 and b with u-boundaries.

This integral definitely grows infinitely large as x approaches infinity, so both it and the series will diverge.

The Comparison Test

NOTE. The Comparison Test is also called the Direct Comparison Test.

This test is useful when the series at hand looks similar to a series for which you already know—or can easily determine—the convergence. Now that you know how to apply the integral, geometric, and p-series tests, you can use them in conjunction with the Comparison Test in order to determine the convergence of series that are almost (but not quite) geometric or p-series or that are nearly (but not quite) integrable. As was the case with the Integral Test, all the terms of the series involved must be positive to apply the Comparison Test.

ALERT! If a_n ≤ b_n, and b_n is divergent or a_n is convergent, you can draw no conclusions about the other series.

The Comparison Test: If ∑a_n and ∑b_n are both positive series and every term of ∑a_n is less than or equal to the corresponding ∑b_n term,

(1) if ∑b_n converges, then ∑a_n converges.

(2) if ∑a_n diverges, then ∑b_n diverges.

Consider the following diagram of the first few terms of each sequence. Notice that a_n < b_n for all n. The figure also contains the functions a(x) and b(x) from which the terms of the series get their value.

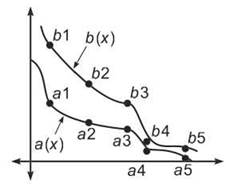
If converges, then according to the Integral Test, is finite. In other words, there is a number that represents the area trapped between b(x) and the x-axis. Since the area beneath a(x) must be less than the area beneath b(x) (since all the function values for a are less than or equal to b's values), then the area beneath a(x) must also be finite. How can an area less than a finite area be infinite? Similarly, if diverges, then the area must be infinite. If b has larger values than this divergent integral, then b_n must be divergent, too.

NOTE. The trickiest part of the Comparison Test is deciding what to compare the given series to. Most of the time, you pick a series that is close to, but simpler than, the given series.

This test works just like the restriction signs for kiddie rides at theme parks: “You cannot be taller than this to ride this ride.” I am too tall to ride kids’ rides, but Papa Smurf can ride any of them. If an individual comes along who is taller than I am, then he will not be able to ride either (the divergence part of the rule). However, if someone shorter than Papa Smurf strolls up, then he will be able to ride (the convergence part of the rule).

Example 6: Use the Comparison Test to determine the convergence of the following series:

a)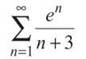

Compare this to the series Without a doubt, the numerator eⁿ is much larger than the other numerator, 1. Therefore, each term of the series will be larger than the comparsion series, However, using the Integral Test, it is easy to see that is divergent. Because is larger than a divergent series, it must also be divergent by the Comparison Test.

(b)

Compare this to the series 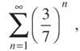which is a convergent geometric series (since r = 3/7, which is less than 1). Since each of the denominators of are greater than the corresponding denominators in the geometric series 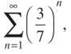that will result in a smaller overall value for each term (in the same way that 1/6 < 1/5, even though 6 > 5). Therefore, is smaller than a convergent series, so it must be convergent, too.

The Limit Comparison Test

TIP. When choosing the comparison series, use only the highest powers of n in the numerator and denominator of the original series.

This test operates in a slightly different way from previous tests but has many of the same characteristics as the Comparison Test. For one thing, you’ll need to invent a comparison series, and both your original and the new series must contain positive terms. In practice, the Limit Comparison Test allows you to take ugly series and compare them to very simple p-series to determine their convergence. There is even good news, pessimistic mathematician: It’s very easy to pick a comparison series with this test. When you’ve stopped cheering, you may continue reading.

The Limit Comparison Test: If ∑a_n and ∑b_n are positive series, and

(where N is a positive number), then both series either converge or diverge. If the limit does not equal a finite number, you can draw no conclusion from this test.

Translation: To determine whether or not a series ∑a_n converges, you will first invent a comparison series ∑b_n. Then, find the limit at infinity of the quotient a_n/b_n. If that limit exists (in other words, if the limit is a finite number), then either both series will converge or both will diverge. Because of this, you should choose a ∑b_n that is obviously convergent or divergent to cut down on your work.

Just like the Comparison Test, the convergence or divergence of the series, a_n, is dependent upon the convergence of the series to which it is compared, b_n. Although a bit strange, the Limit Comparison Test is more straightforward than its predecessor and is, in practice, easier to use.

Example 7: Use the Limit Comparison Test to determine whether or not the following series converge:

a)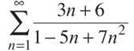

As the tip above explains, use the highest powers of n in the numerator and denominator to create a comparison series of n/n² or 1/N.

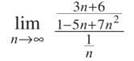
Multiply the numerator and denominator of this mega fraction by n/1 to get

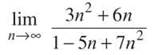
Because this is a rational function with equal degrees in the numerator and denominator, the limit is the ratio of the leading coefficients: 3/7. Therefore, both series will either converge or diverge; so which is it? We already know that ∑1/n diverges, so both series diverge. If you forgot that it was a harmonic series, you still know that ∑1/n is a divergent p-series (since p = 1).

(b)

This one is trickier. You’re supposed to use the highest powers of n only, so what do you do with the 4ⁿ? Answer: include it also—with an n power, it has to be important. Therefore, the comparison series is or

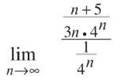
CAUTION. A limit of 1/3 does not mean that either series has a sum of 1/3. All that’s important is that 1/3 is a finite number (not ∞).

Multiply the top and bottom of that giant fraction by 4ⁿ to get

We got the number we needed—now, to determine if the series converge or not. The comparison series can be rewritten as which is a convergent geometric series (since r = 1/4 < 1). Therefore, both of the series must be convergent.

The Ratio Test

Yet again, this test works only for series with positive terms. (The next series test will finally address series with positive and negative terms.) The Ratio Test works best for series that contain things that grow extremely large as n increases, like powers of n or factorials involving n. In essence, you take the limit at infinity of the ratio of a generic series term a_n and the next consecutive generic term a_n+1; you can determine the convergence of the series based on what happens after you find the limit.

The Ratio Test: If ∑a_n is a series whose terms are positive, and

(where A is a real number), then

(1) ∑a_n converges if N < 1.

(2) ∑a_n diverges if N > 1.

(3) If N = 1, we don’t know diddly squat: the series could converge or diverge, but to determine which, we’ll have to use a different test; the Ratio Test doesn’t help.

Example 8: Use the Ratio Test to determine whether or not the following series converge:

a)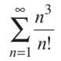

Your best bet is the Ratio Test because of the factorial in the series. In this case, a_n = n³/n!; to get a_n+1, substitute (n + 1) for n:

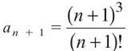
Now you can set up the limit that is the heart of the Ratio Test:

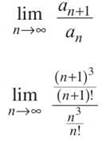
To simplify the fraction, multiply the numerator and denominator by the reciprocal of the denominator. (This is always the second step.)

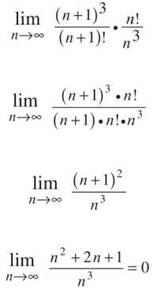
The limit at infinity is 0; since 0 < 1, the series converges according to the Ratio Test.

(b)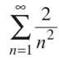

This doesn’t have anything that grows so large as to make the Ratio Test our first choice, but we have to follow directions.

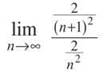
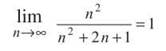
Since the limit equals 1, no conclusion can be drawn using the Ratio Test. So, let’s try something else even though the directions don’t tell us to—we’re rebels! Notice that 2/n² is almost a p-series, so the better bet would have been the Limit Comparison Test. A good comparison series is 1/n²:

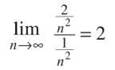
Because 2 is a finite number (and 1/n² is a convergent p-series) both series converge according to the Limit Comparison Test.

The Alternating Series Test

Until now, you have determined convergence for lots of different series. Most of those tests required the terms of the series to be positive. Finally (exhale here), the Alternating Series Test (inhale nervously here) allows you to consider series with negative terms. However, these series must alternate back and forth between positive and negative terms. For example, 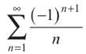is an alternating series:

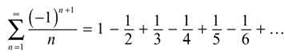
The series has a positive term, then a negative term, then a positive term, etc. In contrast, the series

is not an alternating series. Not only do the signs have to alternate, but they also have to alternate every other term.

The Alternating Series Test: If ∑a_n is an alternating series; each term, a_n+1, is smaller than the preceding term a_n; and then ∑a_n converges.

Translation: In order for an alternating series to converge, (1) the terms must decrease as n increases (in fact, each term has to be smaller than the term before it), and (2) the series must pass the nth Term Divergence Test—the nth term must have a limit of 0. If both conditions are satisfied, the alternating series converges.

TIP. Once you know a series is alternating, you can ignore the negative signs as you proceed through the test.

Example 9: Determine whether or not the following series converge using the Alternating Series Test:

(a)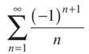

It’s the alternating series form of a harmonic series. You may want to answer “divergent” as a reflex. Let’s see what happens. If we write out a few terms

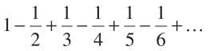
it’s clear that this is an alternating series and that each term is smaller than the previous one. Don’t worry about the positive and negative signs. Clearly, etc. That satisfies the first requirement of the test. The second requirement involves the following limit:

The limit is very easy to find, and we again ignore the possibility of a negative sign when evaluating the limit. The test takes care of the negative sign without our having to worry about it. Because both conditions are satisfied, this series converges.

b)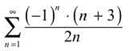

To begin, let’s write out a few terms of the series:

The series is definitely alternating, and (ignoring the signs) each term is less than the term preceding it. However,

Therefore, this series fails the second condition of the Alternating Series Test. In fact, this series outright fails the nth Term Divergence Test and therefore diverges. Even though it’s an alternating series, it (like all series) m list pass the nth Term Divergence Test in order to converge.

In some series, the alternating series test will not apply, even though we want it to so badly. Let’s take, for example, The series definitely alternates; that’s not the problem. If we write a few terms out, we get

The terms (at least in this small sample) definitely don’t seem to be getting uniformly smaller. They will later, but at first, things are pretty weird. Furthermore, let’s try to find the required limit for the Alternating Series Test:

This is the indeterminate form ∞/∞, so our natural instinct would be to use L’Hopital’s Rule. How do we find the derivative of (n!)? Things are looking ugly—the Alternating Series Test isn’t cutting the mustard. In cases such as these, we will look for absolute convergence. It will allow us to ignore the pesky negative signs and still determine if the alternating series converges.

Absolute Convergence: If ∑│a_n│ converges, then ∑a_n is said to converge absolutely, and the original series, ∑a_n, automatically converges. If ∑│a_n│ diverges but ∑a_n converges, the series is said to converge conditionally.

Example 10: Does converge?

Solution: Because the Alternating Series Test doesn’t work, as we showed above, we will test to see if

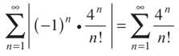
converges instead. Because of the large quantities involved, the Ratio Test is your best bet.

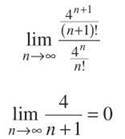
Because 0 < 1, this series converges by the Ratio Test. Here’s the great part: Because the absolute value of the series converged, the series converges absolutely, and converges automatically! Handy, eh?

You may wonder why absolute convergence works. In essence, it says to ignore all negative terms in a series and make them positive. If that all-positive series still converges to a single number, then allowing some of those terms to be negative will not cause that sum to get any larger and possibly diverge. In fact, the inclusion of negative terms will make that sum smaller.

The final important characteristic of alternating series is the error-bound that they can report. Like most other series tests (excluding geometric), you cannot find the sum of the infinite series. You still can’t with Alternating Series (Booooo!), but you can tell approximately how close your partial sum approximation is. Here’s the important factoid to remember: The error inherent in an alternating series ’partial sum S_n is less than the absolute value of the next term, a_n+1. This may sound tricky, but it’s really easy!

Example 11: Find the interval in which the actual sum of 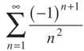is contained if S₅ is used to approximate it.

Solution: S₅ is the partial sum that includes only the first five terms of the series. So, this problem is approximating the sum of the series by adding only those terms together:

Although that’s not the sum of the infinite series, we will soon be able to tell just how close of an approximation it is. The maximum possible error will be the absolute value of the next term, The actual infinite sum for the series will fall within .027777 of .838611. Therefore, the actual sum is somewhere in the interval

(.838611 - .027777,.838611 + .027777)

(.810833,.866388)

Conclusion

After learning all of these tests for series convergence, most students think that it will be a miracle if they can simply remember them all on a test—I agree. However, it is a miracle that helps me remember all the tests. Whenever you face an ugly, squirming, gross series problem, remember Moses parting the Red Sea. Not only is it relaxing, it also forms a mnemonic phrase to help you remember all the series you’ve learned:

PARTING C

(Okay, I had to be a little creative with “C,” but cut me some slack.) Each letter represents one of the tests you just learned. As you attempt each of the problems in the Problem Set, use the Moses phrase to help decide which test to use:

P P-series: Is the series in the form

A Alternating series: Does the series alternate? If it does, are the terms getting smaller, and is the nth term 0?

R Ratio Test: Does the series contain things that grow very large as n increases?

T Telescoping series: Will all but a couple of the terms in the series cancel out?

I Integral Test: Can you easily integrate the expression that defines the series?

N Nth Term Divergence Test: Is the nth term something other than 0?

G Geometric series: Is the series of the form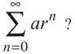

C Comparison Tests: Is the series almost another kind of series (e.g., p-series or geometric series)? Which would be better to use: the Comparison or the Limit Comparison Test?

Just think of it: Moses was fleeing from the Egyptians and captivity. You’ve probably never had to part anything larger than your hair. Unless you are a member of the ’80s band Poison, the tasks aren’t even comparable.

EXERCISE 2

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

DO NOT USE A GRAPHING CALCULATOR FOR ANY OF THESE PROBLEMS.

For 1 through 12, determine whether or not the series converge using the appropriate convergence test (there may be more than one applicable test). If possible, give the sum of the series.

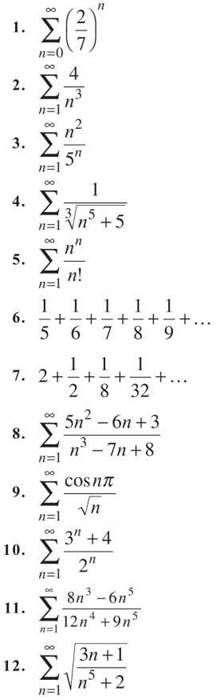
13. Determine if the series 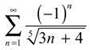converges absolutely, converges conditionally, or diverges.

ANSWERS AND EXPLANATIONS

1. This is a geometric series with a = 1 and r = 2/7. Because 0 < 2/7 < 1, the series will converge, and it will converge to

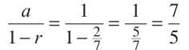
2. This looks like a p-series with p = 3. However, the 4 makes it a little different. Because the 4 will be multiplied by every term in the series, we can rewrite the series as

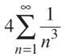
(You can pull out the constant, just like you did with definite integrals.) Therefore, the 4 does not affect the series at all. Since p > 1, the series converges.

3. This series is a good candidate for the Ratio Test because of 5ⁿ; this quantity will grow large quickly as n increases.

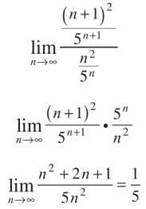
Because 1/5 < 1, this series converges according to the Ratio Test. (Remember, 1/5 just tells you that the series converges—it does not mean that the sum of the series is 1/5.)

4. Compare this to the series 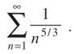The original series has denominators that are slightly greater than each corresponding denominator in the second series. A larger denominator means a smaller value. Therefore, each term of 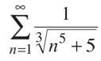will be smaller than the corresponding term of Notice that 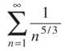is a simple p-series, and since p = 5/3 > 1, it converges. Because 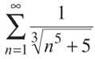is smaller than a convergent series, it must converge by the Comparison Test, too.

5. The Ratio Test is our best bet, as nⁿ and n! will grow large quickly as n increases.

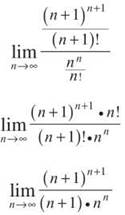
You can cancel an (n + 1) term out of the top and bottom, leaving you with

Here’s the tricky part: If you rewrite this limit, you get

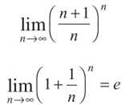
Remember that limit you memorized a long time ago? There it is again. Since e > 1 (e is approximately 2.718), the series diverges.

6. This is actually the series 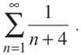Use the Integral Test to see if it converges.

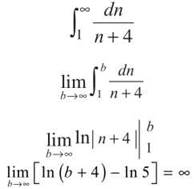
Therefore, both the integral and the series diverge.

7. This is a geometric series with a = 2. F actor 2 out of all the terms in the series to get the following ratio:

The denominators are consecutive powers of 4, so the ratio is r = 1/4, and the series is 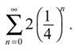The series converges since 1/4 is between 0 and 1, and it has sum

8. This is a Limit Comparison problem. Take the highest powers of the numerator and denominator to create the comparison series

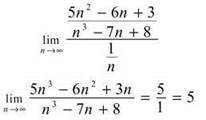
Since 1/n is a divergent p-series, and the above limit exists, both series diverge by the Limit Comparison Test.

9. Although this series looks funky, it’s just an alternating series. The numerators will be cos π, cos 2π, cos 3π, cos 4π, etc., which are just the numbers 1, —1, 1, —1, etc. Each successive term will definitely get smaller (since the denominators will grow steadily). Therefore, all that’s left in the Alternating Series Test is the limit:

The limit does equal zero (consider the graph). Therefore, this alternating series converges by the Alternating Series Test.

10. Each term of this series is greater than each corresponding term of the 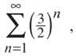which is a divergent geometric series. Because 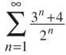is greater than a divergent series, it must diverge by the Comparison Test, too.

11. Although this problem may look complicated, it is actually quite easy. This series diverges by the nth Term Divergence Test. Notice that

Because the limit at infinity of the nth term is not 0, this series cannot converge (you will eventually be adding —2/3 forever).

12. If you rewrite the series as

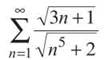
you can use the Limit Comparison Test. Take the highest powers of n in the numerator and denominator to create the comparison series

(If you leave unsimplified, it’s more obvious to multiply the radicals together.)

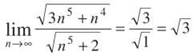
Because is a convergent p-series, both series must converge.

13. First of all, test the absolute convergence by ignoring the (—1)ⁿ. This gives the series This is similar to the p-series so use the Limit Comparison Test:

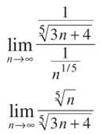
Because this is a rational function with equal powers in both parts of the fraction, the limit is Because that is a finite number, both series diverge according to the Limit Comparison Test. The conclusion? This series does not converge absolutely. Next, we need to determine whether or not the series converges conditionally by leaving the (—1)ⁿ in place.

The series is definitely alternating, and, because the denominators will grow steadily, the terms will lessen in value as n increases. Now, to test the nth term (the last hurdle in the Alternating Series Test):

According to the Alternating Series Test, this series converges but only conditionally, since the absolute value of the series diverged.