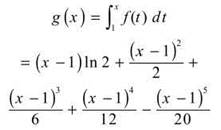Master AP Calculus AB & BC

Part III. FOUR PRACTICE TESTS

ANSWER KEY AND EXPLANATIONS

Section I, Part A

1. The correct answer is (D). This is a straight-forward u-substitution integration problem. If we let u = sinx, then du = cosx dx and

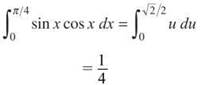
2. The correct answer is (D). Remember that 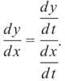First, we’ll find

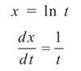
Now, we’ll find

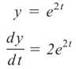
So,

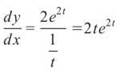
3. The correct answer is (A). To find the local minimum, we need to determine when the derivative changes from negative to positive. First, we determine the derivative:

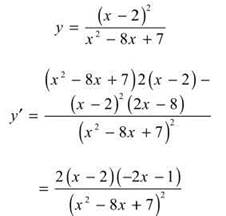
If we set y' = 0 and solve for x, we see that x = —1/2 and x = 2 are zeros of the derivative. By examining the wiggle graph below, we can see that the local minimum occurs at x = —1/2.

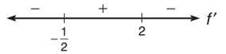
4. The correct answer is (D), This problem calls for the product rule. We must differentiate each term with respect to x.

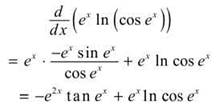
5. The correct answer is (C). Here, we use the quotient rule to determine the derivative; then, evaluate it at x = π.

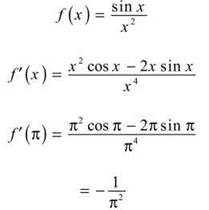
6. The correct answer is (A). The graph of h(x) is concave down for all x < 0 and concave up for all x > 0. This implies that the second derivative is negative for all x < 0 and positive for all x > 0. Choice (A) is the only graph that meets this requirement.

7. The correct answer is (D). To write the equation of a tangent line, we need a point and the slope. The point is given to us: (3,2). The slope is merely they-coordinate that corresponds to x = 3 on the graph of f'. Since f'(3) = —2, then the slope of the tangent line is —2. In point-slope form, the equation of the tangent line is

y — 2 = —2(x — 3)

8. The correct answer is (D). This is an area accumulation problem. We can see that the accumulated area is least when x = 4.

9. The correct answer is (B). Points of inflection on the graph of a function correspond to horizontal tangents on the graph of the derivative. Since there are three, the function has three points of inflection.

10. The correct answer is (B). This is an implicit differentiation problem. Remember, we need to use the product rule to differentiate 2xy².

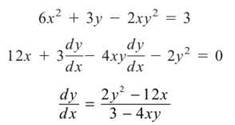
Now, we determine the corresponding y value by substituting x = 0 into the original equation.

0 + 3y - 0 = 3

y = 1

Finally, we substitute x = 0 and y = 1 into dy/dx.

11. The correct answer is (B). For an improper integral, we first change it to a limit of a definite integral.

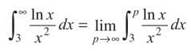
Now, we have to address that tricky integrand. We do integration by parts and let u = ln x and dv = x^-2dx. So,

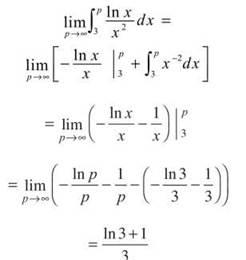
Note: by L’Hopital’s rule.

12. The correct answer is (D). This is an example of a straightforward integration-by-parts problem. We let u = x and dv = sec²x dx.

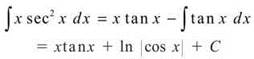
13. The correct answer is (A). If we try to evaluate this limit using direct substitution, we will get an indeterminate form: 0/0. So, we can use L’Hopital’s rule and take the derivative of the numerator and denominator; then, evaluate the limit.

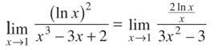
If we evaluate the limit now, we still get 0/0. So, we try L’Hopital’s rule again.

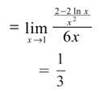
14. The correct answer is (A), cosx centered at x = 0 is one Taylor polynomial that we should be able to generate from memory. It goes like this:

To find the value for cos2, we substitute 2 for x:

15. The correct answer is (D). Both I. and II. converge to 0, while III. is divergent.

16. The correct answer is (A). Since acceleration is associated with the second derivative of position, we must determine the second derivative for each of these parametric equations and evaluate them at x = 2.

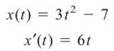
Rewrite y(t) as

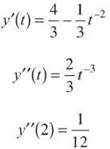
The acceleration vector of the particle at x = 2 is

17. The correct answer is (B). Notice that all of the slopes on the line y = x are zero.

18. The correct answer is (B). This is a well-disguised application of L’Hopital’s rule. We should take the derivative of the numerator and the derivative of the denominator and then evaluate the limit.

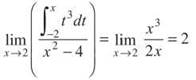
Notice we use the Fundamental Theorem, Part Two to determine the derivative of the numerator.

19. The correct answer is (D). When integrating a rational expression with a numerator of greater degree than the denominator, we first divide and then integrate.

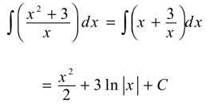
20. The correct answer is (C). We will determine the derivative of this function by using both the power and chain rules. Then, we will evaluate it at x = π/3.

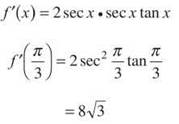
21. The correct answer is (B). This is asking for the derivative of the derivative when x = 3. So, we need the second derivative of the function.

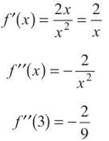
22. The correct answer is (E). Since the degree of the numerator is greater than the degree of the denominator, the limit as x approaches infinity does not exist because it is infinite.

23. The correct answer is (D). The trick to this problem is to recognize that

So now all we need to find is the derivative of secx²cosx², which is equal to 1. The derivative of 1 is 0.

24. The correct answer is (D). Remember the trapezoidal rule:

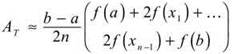
Applying this to the function y = x² — 2x + 1 over [0,4] with n = 4 yields

25. The correct answer is (D). This function is We integrate this from x = 0 to x = 2.

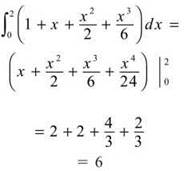
26. The correct answer is (B). By reading the graph, we can tell that f(2) < 0. Since there is a horizontal tangent line at x = 2, f'(2) = 0. f"(2) > 0 because the curve is concave up at x = 2. Therefore, f(2) < f'(2) < f"(2).

27. The correct answer is (C). This is a rather complicated w-substitution integration problem. If we let u = √x, then

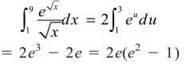
28. The correct answer is (C). We need to determine dx/dt and dy/dt first.

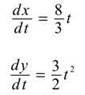
Now, we integrate from x = 0 to x = 2 the square root of the sum of the squares of dx/dt and dy/dt.

Section I, Part B

29. The correct answer is (A). If we let k = 2, the first series becomes 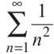and converges since it is a p-series with p > 1. If k = 2, the second series becomes 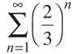and converges since it is a geometric series with R < 1.

30. The correct answer is (D). Begin by drawing a diagram.

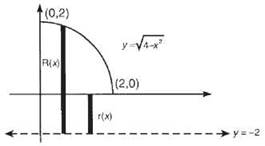
You could use the shell method, but well use the washer method. Use vertical rectangles, since they are perpendicular to the horizontal axis of rotation. R(x) is the outer radius, and R(x) is the inner radius.

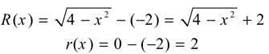
Now, apply the washer method:

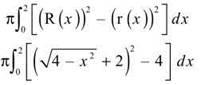
Use your graphing calculator to evaluate the integral. The volume will be 56.234.

31. The correct answer is (B). We must determine the second derivative for each component:

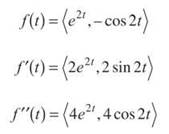
32. The correct answer is (A). This is an integration by parts with a twist toward the end. Let’s let u = sinx and dv = e^x dx, so

We need to integrate by parts again. Well let u = cosx and dv = e^x dx, continuing:

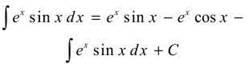
Here’s the twist. We are going to add ∫(e^xsinx) dx to both sides of the equation:

To solve for ∫(e^xsinx) dx, we will divide both sides by 2:

33. The correct answer is (B). In order to succeed with this problem, we must readily recognize slight variations of series that we have memorized previously. Remember the Maclaurin series for cosx:

The series in this problem is the Maclaurin series for cos2x. So, we are being asked to determine at what x value the graphs of y = cos2x and y = 3x³ — 2x² + 7 intersect. Our calculators will tell us that happens when x = —1.180.

34. The correct answer is (B). We are going to determine the antiderivative of each component of the acceleration vector, solve for the constants of integration, and plug and chug to determine the velocity vector when t = 1. First, we deal with the x component:

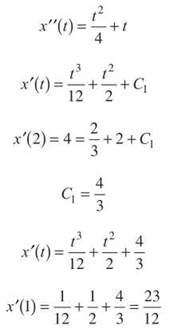
Now, we do it all again for y:

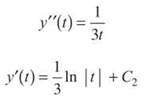
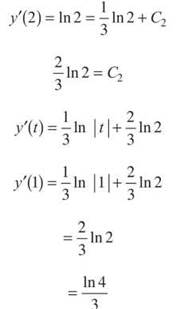
Note that (by log properties).

Finally, the velocity vector of the particle when t = 1 is

35. The correct answer is (B). To find the average rate of change of a function over an interval, we need the slope of the secant line over that interval.

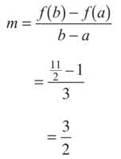
36. The correct answer is (E). We need to find the equation for the tangent line of the graph at x = 2 and use our calculator to determine where that line crosses the x-axis. Remember, to write an equation for a tangent line, we need a point on the line and the slope of the line. Since f(2) = 4, (2,4) is on the line. The slope is

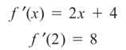
Using point-slope form,

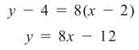
Using the calculator (or maybe your head), x = 1.5 is a zero of y = 8x - 12.

37. The correct answer is (A). We have to use the method of partial fractions in order to get the integrand into a form that is integrable. To start, since the degrees of the numerator and denominator are equal, we use polynomial long division. So,

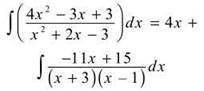
To integrate use partial fractions:

Multiply through by (x + 3)(x—1) to get

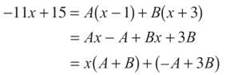
This gives you the system of equations A + B = —11 and —A + 3B = 15. Solving simultaneously, we get:

A = —12 and B = 1

The integral can now take the easier form

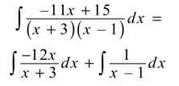
Continuing with the integration from above:

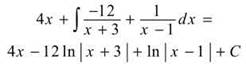
38. The correct answer is (C). For this problem, we need to realize that profits = revenue — cost. So, to find profits,

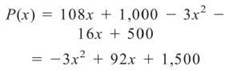
The derivative is P'(x) = —6x + 92. Set this equal to zero, and we find that P(x) is maximized at

39. The correct answer is (D). To determine the interval of convergence, we take the limit of the ratio test.

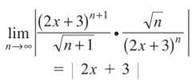
│2x + 3│ converges if it is less than 1.

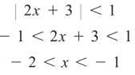
By testing the endpoints, we find that the series converges when x = —2 and diverges when x = —1. So the interval of convergence is —2 ≤ x < —1.

40. The correct answer is (C). In order for the limit to exist, the left- and right-hand limits have to exist and be equal to each other. Since both of these are equal to 2,

41. The correct answer is (C). Because we get 0/0 when we try to evaluate by direct substitution, we need to use L’Hopital’s rule on this limit.

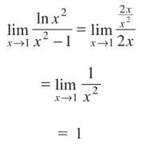
42. The correct answer is (A). The quickest and easiest way to attack this problem is by graphing it. Which v-value makes both the first and second derivatives negative?

43. The correct answer is (B). Whenever the rate of a function increasing or decreasing is proportional to itself, it must be an exponential function of the form P(t) = Ne^kt. N is the initial value, so in this case, N = 40. We use P(1) = 48.856 to determine the value of k.

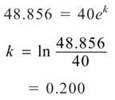
To determine how long it will take the population to double,

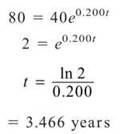
44. The correct answer is (B). Rolle’s theorem deals with the idea that if the function passes through the same y-coordinate twice, it must have a zero derivative somewhere between these two points.

45. The correct answer is (B). Since the velocity is positive, the position function must be increasing. Since the velocity is increasing, the position function must be concave up. The only choice to meet both of these requirements is choice (B).

Section II, Part A

1. (a)

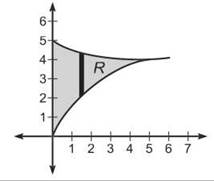
(b)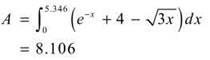

(c) We use the washer method to determine the volume:

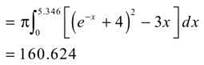
(d) It would be good to know that the area of an equilateral triangle with side 5 is given by So, the volume of this solid would be given by

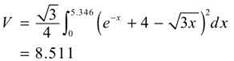
2. (a) Since the rate of decrease is proportional to the function itself, we have an exponential function of the following form:

A(t) = Ne^kt

Since the tire initially had 1,500 cubic inches of air, C = 1500. We are given that A(1) = 1,400:

1,400 = 1500e^k

Solving for k,

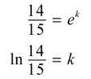
Substituting this expression for k yields

(b) Since 2/3 of 1,500 is 1,000, we can substitute 1,000 into the formula for A (t) and solve for t:

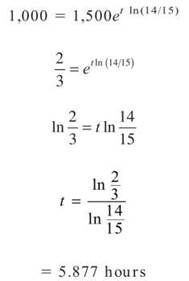
3. (a) We have to use implicit differentiation and differentiate with respect to x:

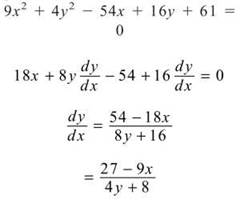
(b) Vertical tangent lines exist wherever the denominator of the derivative equals zero, and the numerator does not. So, we determine where the denominator is equal to zero.

4y + 8 = 0

y = -2

Since we are writing the equation for one or more vertical lines, we really need to know the corresponding x-coordinate(s). To this end, we will substitute y = —2 into the original equation and solve for x.

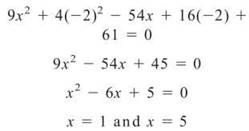
So, the equations for the vertical tangent lines are x = 1 and x = 5.

(c) We will first find the slope, write the equation in point-slope form, and then convert to slope-intercept form.

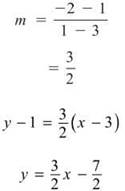
(d) Since the lines are parallel, they have equal slopes. So, the slope of the tangent line is 3/2. Now, we need the point(s) on the curve where the derivative is equal to 3/2. To determine this, we set the derivative equal to 3/2, solve for y, substitute back into the original equation, and solve for x.

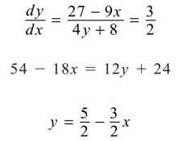
Substituting this expression for y into the original equation and solving for x gives us

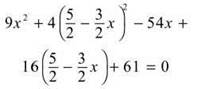
With help from our calculators, x = 1.586 and x = 4.414. By substituting these x-values into , we get the corresponding y-values to be y = 0.121 and y = —4.121, respectively. So, there are two tangent lines parallel to the line from part C; they have the following equations:

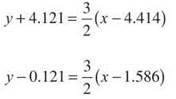
Section II, Part B

4. (a) The bug changes directions at t = 3 and t = 5. This is true because the velocity changes from positive to negative and negative to positive, respectively.

(b) The bug is farthest from its starting point at time t = 3. The bug is moving in the positive direction (away from the starting point) from t = 0 to t = 3. Then, the bug turns around and moves toward the starting point for two seconds before changing directions again. By examining the area under the curve, we can see that the bug is closer to the starting point at t = 6 then it was at t = 3.

(c) “Slowing down” means decreasing speed, not velocity. So, we need to include not only where the velocity is positive and decreasing, but also where the velocity is negative and increasing. The velocity is positive and decreasing over the interval (1.5,3), and it is negative and increasing over the interval (4,5). So, the bug is slowing down over these two intervals.

5. (a) We want to try to isolate and in order to use the identity sin²x + cos²x = 1. Looking at the x component of the curve, we first square both sides:

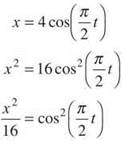
And now for the y component:

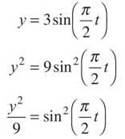
By combining these equations, we get:

(b) Using implicit differentiation,

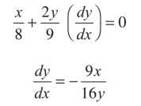
(c)

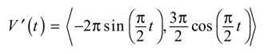
(d) From part C:

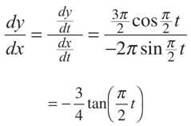
From part B:

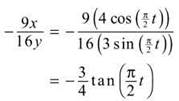
(e) We will use the formula for arc length:

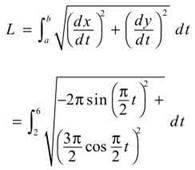
6. (a) Recall the formula for a Taylor polynomial centered at x = 1:

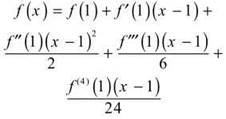
This implies that f(1) = ln 2 and f⁴(1) = -6.

(b)

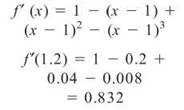
(c)