Calculus AB and Calculus BC
CHAPTER 2 Limits and Continuity
Concepts and Skills
In this chapter, you will review
• general properties of limits;
• how to find limits using algebraic expressions, tables, and graphs;
• horizontal and vertical asymptotes;
• continuity;
• removable, jump, and infinite discontinuities;
• and some important theorems, including the Squeeze Theorem, the Extreme Value Theorem, and the Intermediate Value Theorem.
A. DEFINITIONS AND EXAMPLES
The number L is the limit of the function f (x) as x approaches c if, as the values of x get arbitrarily close (but not equal) to c, the values of f (x) approach (or equal) L. We write
![]()
In order for ![]() to exist, the values of f must tend to the same number L as x approaches c from either the left or the right. We write
to exist, the values of f must tend to the same number L as x approaches c from either the left or the right. We write
One-sided limits
![]()
for the left-hand limit of f at c (as x approaches c through values less than c), and
![]()
for the right-hand limit of f at c (as x approaches c through values greater than c).
EXAMPLE 1
The greatest-integer function g(x) = [x], shown in Figure N2–1, has different left-hand and right-hand limits at every integer. For example,
![]()
This function, therefore, does not have a limit at x = 1 or, by the same reasoning, at any other integer.
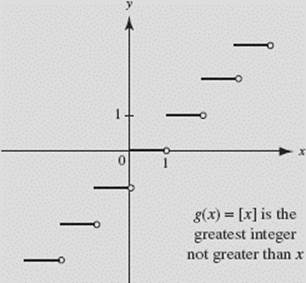
FIGURE N2–1
However, [x] does have a limit at every nonintegral real number. For example,
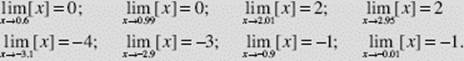
EXAMPLE 2
Suppose the function y = f (x), graphed in Figure N2–2, is defined as follows:
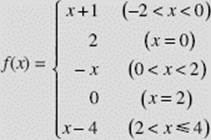
Determine whether limits of f, if any, exist at
(a) x = −2,
(b) x = 0,
(c) x = 2,
(d) x = 4.
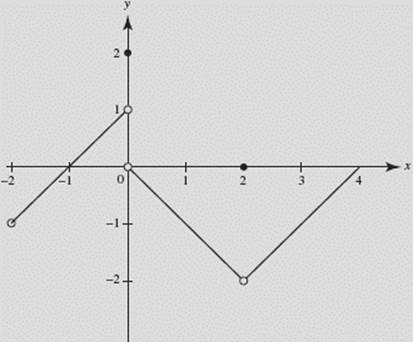
FIGURE N2–2
SOLUTIONS:
(a) ![]() so the right-hand limit exists at x = −2, even though f is not defined at x = −2.
so the right-hand limit exists at x = −2, even though f is not defined at x = −2.
(b) ![]() does not exist. Although f is defined at x = 0 (f (0) = 2), we observe that
does not exist. Although f is defined at x = 0 (f (0) = 2), we observe that ![]() whereas
whereas ![]() For the limit to exist at a point, the left-hand and right-hand limits must be the same.
For the limit to exist at a point, the left-hand and right-hand limits must be the same.
(c) ![]() This limit exists because
This limit exists because ![]() Indeed, the limit exists at x = 2 even though it is different from the value of f at 2 (f (2) = 0).
Indeed, the limit exists at x = 2 even though it is different from the value of f at 2 (f (2) = 0).
(d) ![]() so the left-hand limit exists at x = 4.
so the left-hand limit exists at x = 4.
EXAMPLE 3
Prove that ![]()
SOLUTION: The graph of |x| is shown in Figure N2–3.
We examine both left- and right-hand limits of the absolute-value function as x → 0. Since
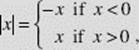
it follows that ![]()
Since the left-hand and right-hand limits both equal 0, ![]()
Note that ![]() if c > 0 but equals −c if c < 0.
if c > 0 but equals −c if c < 0.
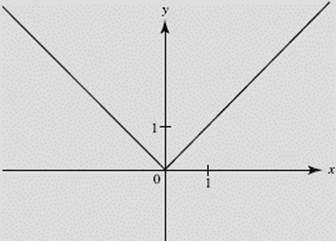
FIGURE N2–3
DEFINITION
The function f (x) is said to become infinite (positively or negatively) as x approaches c if f (x) can be made arbitrarily large (positively or negatively) by taking x sufficiently close to c. We write
![]()
Since for the limit to exist it must be a finite number, neither of the preceding limits exists.
This definition can be extended to include x approaching c from the left or from the right. The following examples illustrate these definitions.
EXAMPLE 4
Describe the behavior of ![]() near x = 0 using limits.
near x = 0 using limits.
SOLUTION: The graph (Figure N2–4) shows that:
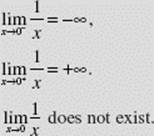
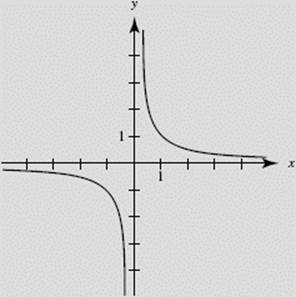
FIGURE N2–4
EXAMPLE 5
Describe the behavior of ![]() near x = 1 using limits.
near x = 1 using limits.
SOLUTION: The graph (Figure N2–5) shows that:
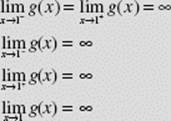
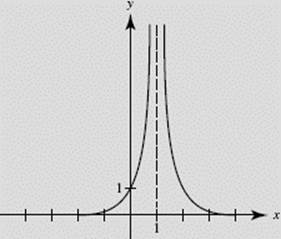
FIGURE N2–5
Remember that none of the limits in Examples 4 and 5 exists!
DEFINITION
We write
![]()
if the difference between f (x) and L can be made arbitrarily small by making x sufficiently large positively (or negatively).
In Examples 4 and 5, note that ![]()
EXAMPLE 6
From the graph of ![]() (Figure N2–6), describe the behavior of h using limits.
(Figure N2–6), describe the behavior of h using limits.
SOLUTION:
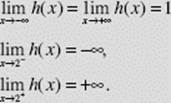
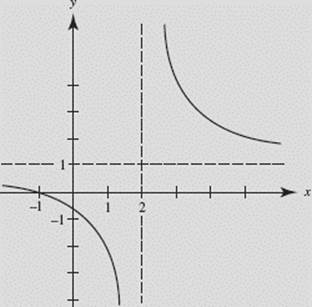
FIGURE N2–6
DEFINITION
The theorems that follow in §C of this chapter confirm the conjectures made about limits of functions from their graphs.
Finally, if the function f (x) becomes infinite as x becomes infinite, then one or more of the following may hold:
![]()
END BEHAVIOR OF POLYNOMIALS
Every polynomial whose degree is greater than or equal to 1 becomes infinite as x does. It becomes positively or negatively infinite, depending only on the sign of the leading coefficient and the degree of the polynomial.
EXAMPLE 7
For each function given below, describe ![]()
(a) f (x) = x3 − 3x2 + 7x + 2
SOLUTION: ![]()
(b) g(x) = −4x4 + 1,000,000x3 + 100
SOLUTION: ![]()
(c) h(x) = −5x3 + 3x2 −4π + 8
SOLUTION: ![]()
(d) k(x) = π − 0.001x
SOLUTION: ![]()
It’s easy to write rules for the behavior of a polynomial as x becomes infinite!