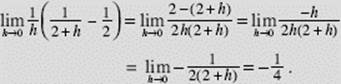Calculus AB and Calculus BC
CHAPTER 2 Limits and Continuity
C. THEOREMS ON LIMITS
If lim f (x) and lim g(x) are finite numbers, then:
(1) lim kf (x) = k lim f (x).
(2) lim[f (x) + g(x)] = lim f (x) + lim g(x).
(3) lim f (x)g(x) = (lim f (x))(lim g(x)).
(4) 
(if lim g(x) ≠ 0).
(5) 
(6) THE SQUEEZE OR SANDWICH THEOREM. If f (x) ≤ g(x) ≤ h(x) and if 
Figure N2–8 illustrates this theorem.
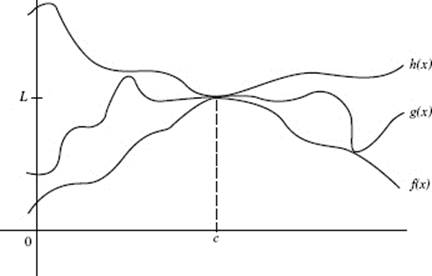
FIGURE N2–8
Squeezing function g between functions f and h forces g to have the same limit L at x = c as do f and g.
EXAMPLE 9
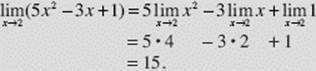
EXAMPLE 10
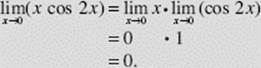
EXAMPLE 11
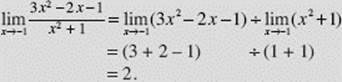
EXAMPLE 12
since, by the definition of 
in §A, x must be different from 3 as x → 3, the factor x − 3 may be removed before taking the limit.
EXAMPLE 13
EXAMPLE 14
the numerator approaches 1 while the denominator approaches 0; the limit does not exist.
EXAMPLE 15
EXAMPLE 16
EXAMPLE 17
