Calculus AB and Calculus BC

CHAPTER 3 Differentiation

Concepts and Skills

In this chapter, you will review

• derivatives as instantaneous rates of change;

• estimating derivatives using graphs and tables;

• derivatives of basic functions;

• the product, quotient, and chain rules;

• implicit differentiation;

• derivatives of inverse functions;

• Rolle’s Theorem and the Mean Value Theorem.

In addition, BC Calculus students will review

• derivatives of parametrically defined functions;

• L’Hôpital’s Rule for evaluating limits of indeterminate forms.

A. DEFINITION OF DERIVATIVE

At any x in the domain of the function y = f (x), the derivative is defined as

The function is said to be differentiable at every x for which this limit exists, and its derivative may be denoted by f ′(x), y ′, or D_x y. Frequently Δx is replaced by h or some other symbol.

The derivative of y = f (x) at x = a, denoted by f ′(a) or y ′(a), may be defined as follows:

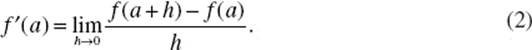
• Difference quotient

• Average rate of change

• Instantaneous rate of change

• Slope of a curve

The fraction is called the difference quotient for f at a and represents the average rate of change of f from a to a + h. Geometrically, it is the slope of the secant PQ to the curve y = f (x) through the points P(a, f (a)) and Q(a + h, f (a + h)). The limit, f ′(a), of the difference quotient is the (instantaneous) rate of change of f at point a. Geometrically, the derivative f ′(a) is the limit of the slope of secant PQ as Q approaches P; that is, as h approaches zero. This limit is the slope of the curve at P. The tangent to the curve at P is the line through P with this slope.

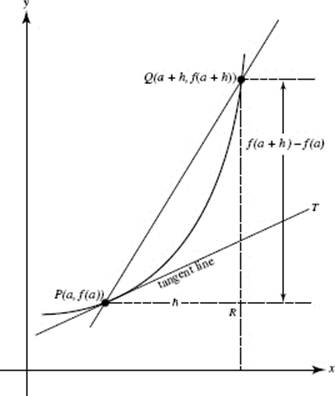
FIGURE N3–1a

In Figure N3–1a, PQ is the secant line through (a, f (a)) and (a + h, f (a + h)). The average rate of change from a to a + h equals which is the slope of secant PQ.

PT is the tangent to the curve at P. As h approaches zero, point Q approaches point P along the curve, PQ approaches PT, and the slope of PQ approaches the slope of PT, which equals f ′(a).

If we replace (a + h) by x, in (2) above, so that h = x − a, we get the equivalent expression

See Figure N3–1b.

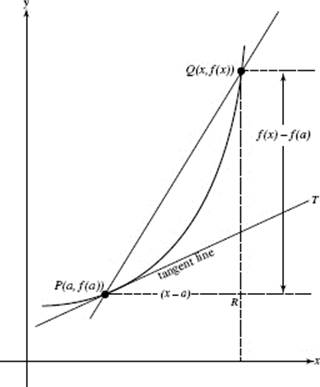
FIGURE N3–1b

The second derivative, denoted by f ″(x) or or y ″, is the (first) derivative of f ′(x). Also, f ″(a) is the second derivative of f (x) at x = a.