Calculus AB and Calculus BC
CHAPTER 3 Differentiation
F. DERIVATIVES OF PARAMETRICALLY DEFINED FUNCTIONS
Parametric equations were defined previously in Chapter 1.
If x = f (t) and y = g(t) are differentiable functions of t, then
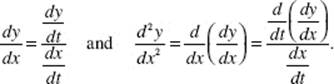
EXAMPLE 24
If x = 2 sin θ and y = cos 2θ, find ![]()
SOLUTION: 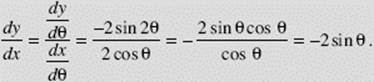
Also,
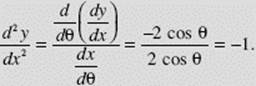
EXAMPLE 25
Find the equation of the tangent to the curve in Example 24 for ![]()
SOLUTION:
When ![]() the slope of the tangent,
the slope of the tangent, ![]() equals −2 sin
equals −2 sin ![]() = −1. Since
= −1. Since ![]() the equation is
the equation is
![]()
EXAMPLE 26
Suppose two objects are moving in a plane during the time interval 0 ≤ t ≤ 4. Their positions at time t are described by the parametric equations
x1 = 2t, y1 = 4t − t2 and x2 = t + 1, y2 = 4 − t.
(a) Find all collision points. Justify your answer.
(b) Use a calculator to help you sketch the paths of the objects, indicating the direction in which each object travels.
BC ONLY
SOLUTION:
(a) Equating x1 and x2 yields t = 1. When t = 1, both y1 and y2 equal 3. So t = 1 yields a true collision point (not just an intersection point) at (2,3). (An intersection point is any point that is on both curves, but not necessarily at the same time.)
(b) Using parametric mode, we graph both curves with t in [0,4], in the window [0,8] × [0,4] as shown in Figure N3–7.
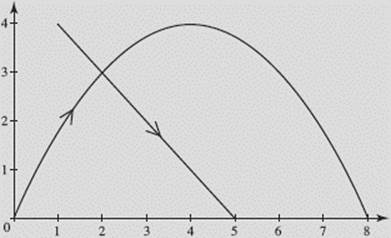
FIGURE N3–7
We’ve inserted arrows to indicate the direction of motion.
Note that if we draw the curves in simultaneous graphing mode, we can watch the objects as they move, seeing that they do indeed pass through the intersection point at the same time.