Calculus AB and Calculus BC
CHAPTER 3 Differentiation
H. DERIVATIVE OF THE INVERSE OF A FUNCTION
Suppose f and g are inverse functions. What is the relationship between their derivatives? Recall that the graphs of inverse functions are the reflections of each other in the line y = x, and that at corresponding points their x- and y-coordinates are interchanged.
Figure N3–8 shows a function f passing through point (a,b) and the line tangent to f at that point. The slope of the curve there, f ′(a), is represented by the ratio of the legs of the triangle, ![]() When this figure is reflected across the line y = x, we obtain the graph of f −1, passing through point (b,a), with the horizontal and vertical sides of the slope triangle interchanged. Note that the slope of the line tangent to the graph of f −1 at x = b is represented by
When this figure is reflected across the line y = x, we obtain the graph of f −1, passing through point (b,a), with the horizontal and vertical sides of the slope triangle interchanged. Note that the slope of the line tangent to the graph of f −1 at x = b is represented by ![]() the reciprocal of the slope of f at x = a. We have, therefore,
the reciprocal of the slope of f at x = a. We have, therefore,
![]()
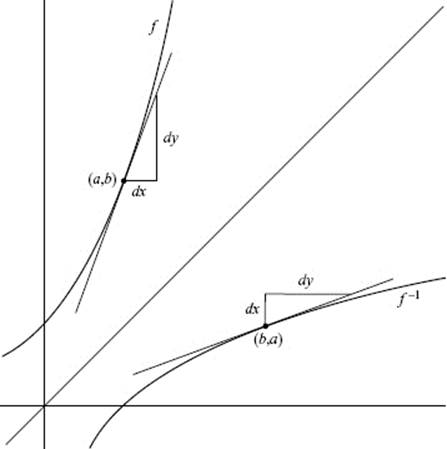
FIGURE N3–8
Simply put, the derivative of the inverse of a function at a point is the reciprocal of the derivative of the function at the corresponding point.
EXAMPLE 32
If f (3) = 8 and f ′(3) = 5, what do we know about f −1?
SOLUTION: Since f passes through the point (3,8), f −1 must pass through the point (8,3). Furthermore, since the graph of f has slope 5 at (3,8), the graph of f −1 must have slope ![]() at (8,3).
at (8,3).
EXAMPLE 33
A function f and its derivative take on the values shown in the table. If g is the inverse of f, find g ′(6).
SOLUTION: To find the slope of g at the point where x = 6, we must look at the point on f where y = 6, namely, (2,6). Since f ′(2) = ![]() g ′(6) = 3.
g ′(6) = 3.
|
x |
f (x) |
f ′(x) |
|
2 |
6 |
|
|
6 |
8 |
|
EXAMPLE 34
Let y = f (x) = x3 + x − 2, and let g be the inverse function. Evaluate g ′(0).
SOLUTION: Since ![]() To find x when y = 0, we must solve the equation x3 + x − 2 = 0. Note by inspection that x = 1, so
To find x when y = 0, we must solve the equation x3 + x − 2 = 0. Note by inspection that x = 1, so
![]()
EXAMPLE 35
Where is the tangent to the curve 4x2 + 9y2 = 36 vertical?
SOLUTION: We differentiate the equation implicitly to get ![]() so
so ![]() Since the tangent line to a curve is vertical when
Since the tangent line to a curve is vertical when ![]() we conclude that
we conclude that ![]() must equal zero; that is, y must equal zero. When we substitute y = 0 in the original equation, we get x = ±3. The points (±3,0) are the ends of the major axis of the ellipse, where the tangents are indeed vertical.
must equal zero; that is, y must equal zero. When we substitute y = 0 in the original equation, we get x = ±3. The points (±3,0) are the ends of the major axis of the ellipse, where the tangents are indeed vertical.