Calculus AB and Calculus BC

CHAPTER 3 Differentiation

I. THE MEAN VALUE THEOREM

If the function f (x) is continuous at each point on the closed interval a ≤ x ≤ b and has a derivative at each point on the open interval a < x < b, then there is at least one number c, a < c <b, such that This important theorem, which relates average rate of change and instantaneous rate of change, is illustrated in Figure N3–9. For the function sketched in the figure there are two numbers, c₁ and c₂, between a and b where the slope of the curve equals the slope of the chord PQ (i.e., where the tangent to the curve is parallel to the secant line).

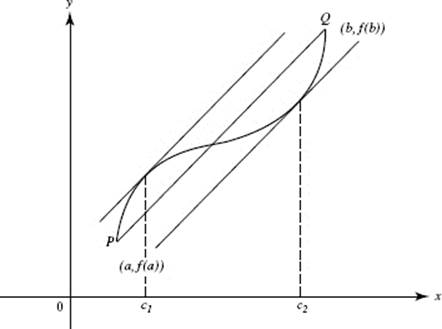
FIGURE N3–9

Rolle’s Theorem

We will often refer to the Mean Value Theorem by its initials, MVT.

If, in addition to the hypotheses of the MVT, it is given that f (a) = f (b) = k, then there is a number, c, between a and b such that f ′(c) = 0. This special case of the MVT is called Rolle’s Theorem, as seen in Figure N3–10 for k = 0.

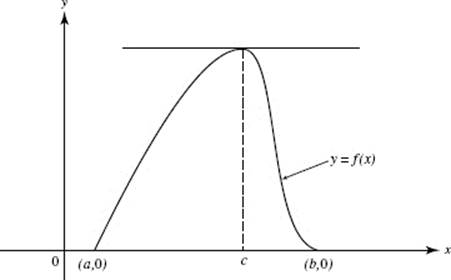
FIGURE N3–10

The Mean Value Theorem is one of the most useful laws when properly applied.

EXAMPLE 36

You left home one morning and drove to a cousin’s house 300 miles away, arriving 6 hours later. What does the Mean Value Theorem say about your speed along the way?

SOLUTION: Your journey was continuous, with an average speed (the average rate of change of distance traveled) given by

Furthermore, the derivative (your instantaneous speed) existed everywhere along your trip. The MVT, then, guarantees that at least at one point your instantaneous speed was equal to your average speed for the entire 6-hour interval. Hence, your car’s speedometer must have read exactly 50 mph at least once on your way to your cousin’s house.

EXAMPLE 37

Demonstrate Rolle’s Theorem using f (x) = x sin x on the interval [0,π].

SOLUTION: First, we check that the conditions of Rolle’s Theorem are met:

(1) f (x) = x sin x is continuous on <0, π > and exists for all x in [0,π].

(2) f ′(x) = x cos x + sin x exists for all x in <0,π >.

(3) f (0) = 0 sin 0 = 0 and f (π) = π sin π = 0.

Hence there must be a point, x = c, in the interval 0 < x < π where f ′(c) = 0. Using the calculator to solve x cos x + sin x = 0, we find c = 2.029 (to three decimal places). As predicted by Rolle’s Theorem, 0 ≤ c ≤ π.

Note that this result indicates that at x = c the line tangent to f is horizontal. The MVT (here as Rolle’s Theorem) tells us that any function that is continuous and differentiable must have at least one turning point between any two roots.