Calculus AB and Calculus BC

CHAPTER 3 Differentiation

J.* INDETERMINATE FORMS AND L’HÔPITAL’S RULE

BC ONLY

Limits of the following forms are called indeterminate:

To find the limit of an indeterminate form of the type we apply L’Hôpital’s Rule, which involves taking derivatives of the functions in the numerator and denominator. In the following, a is a finite number. The rule has several parts:

(a) If and if exists^†, then

if does not exist, then L’Hôpital’s Rule cannot be applied.

^* Although this a required topic only for BC students, AB students will find L’Hôpital’s Rule very helpful.

^† The limit can be finite or infinite (+∞ or −∞).

(b) If the same consequences follow as in case (a). The rules in (a) and (b) both hold for one-sided limits.

(c) If exists, then

if does not exist, then L’Hôpital’s Rule cannot be applied. (Here the notation “x → ∞” represents either “x → + ∞” or “x → −∞.”)

(d) If the same consequences follow as in case (c).

In applying any of the above rules, if we obtain again, we can apply the rule once more, repeating the process until the form we obtain is no longer indeterminate.

Examples 38–43 are BC ONLY.

EXAMPLE 38

is of type and thus equals

(Compare with Example 12 from Chapter 1.)

EXAMPLE 39

is of type and therefore equals

EXAMPLE 40

(Example 13) is of type and thus equals as before. Note that is not the limit of an indeterminate form!

EXAMPLE 41

is of type and therefore equals

EXAMPLE 42

(Example 20) is of type so that it equals which is again of type Apply L’Hôpital’s Rule twice more:

For this problem, it is easier and faster to apply the Rational Function Theorem!

EXAMPLE 43

Find

SOLUTION: is of type and equals

EXAMPLE 44

Find

SOLUTION:

BEWARE: L’Hôpital’s Rule applies only to indeterminate forms Trying to use it in other situations leads to incorrect results, like this:

L’Hôpital’s Rule can be applied also to indeterminate forms of the types 0 · ∞ and ∞ − ∞, if the forms can be transformed to either

EXAMPLE 45

Find

SOLUTION: is of the type ∞ · 0. Since x and, as x → ∞, the latter is the indeterminate form we see that

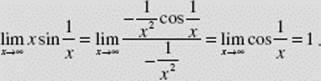
(Note the easier solution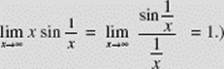

Other indeterminate forms, such as 0⁰, 1^∞ and ∞⁰, may be resolved by taking the natural logarithm and then applying L’Hôpital’s Rule.

BC ONLY

EXAMPLE 46

Find

SOLUTION: is of type 1^∞. Let y = (1 + x)^1/x, so that

ln ln (1 + x). Then ln which is of type Thus,

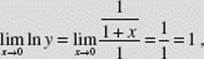
and since ln y = 1, y = e¹ = e.

EXAMPLE 47

Find

SOLUTION: is of type ∞⁰. Let y = x^1/x, so that ln

(which, as x → ∞, is of type ). Then ln and y = e⁰ = 1.

For more practice, redo the Practice Exercises, applying L’Hôpital’s Rule wherever possible.