Calculus AB and Calculus BC

CHAPTER 3 Differentiation

Practice Exercises

Part A. Directions: Answer these questions without using your calculator.

In each of Questions 1–20 a function is given. Choose the alternative that is the derivative, of the function.

1. y = x⁵ tan x

(A) 5x⁴ tan x

(B) x⁵ sec² x

(C) 5x⁴ sec² x

(D) 5x⁴ + sec² x

(E) 5x⁴ tan x + x⁵ sec² x

2.

(A)

(B)

(C)

(D)

(E)

3.

(A)

(B)

(C)

(D)

(E)

4.

(A)

(B) −30(5x + 1)⁻⁴

(C)

(D)

(E)

5. y = 3x^2/3 − 4x^1/2 − 2

(A) 2x^1/3 − 2x^−1/2

(B) 3x^−1/3 − 2x^−1/2

(C)

(D)

(E) 2x^−1/3 − 2x^−1/2

6.

(A)

(B) x^−1/2 + x^−3/2

(C)

(D)

(E)

7.

(A)

(B) 4y(x + 1)

(C)

(D)

(E) none of these

8.

(A)

(B)

(C)

(D)

(E)

9.

(A)

(B)

(C)

(D) 0

(E)

10. y = tan⁻¹

(A)

(B)

(C)

(D)

(E)

11. y = ln (sec x + tan x)

(A) sec x

(B)

(C)

(D)

(E)

12.

(A) 0

(B) 1

(C)

(D)

(E)

13.

(A)

(B)

(C)

(D)

(E)

14.

(A)

(B)

(C)

(D)

(E) cos (ln x)

15.

(A) −csc 2x cot 2x

(B)

(C) −4 csc 2x cot 2x

(D)

(E) −csc² 2x

16. y = e^−x cos 2x

(A) −e^−x (cos 2x + 2 sin 2x)

(B) e^−x (sin 2x − cos 2x)

(C) 2e^−x sin 2x

(D) −e^−x (cos 2x + sin 2x)

(E) −e^−x sin 2x

17. y = sec² (x)

(A) 2 sec x

(B) 2 sec x tan x

(C) 2 sec² x tan x

(D) sec² x tan² x

(E) tan x

18. y = x ln³ x

(A)

(B) 3 ln² x

(C) 3x ln² x + ln³ x

(D) 3(ln x + 1)

(E) none of these

19.

(A)

(B)

(C)

(D)

(E)

20. y = sin⁻¹

(A)

(B)

(C)

(D)

(E)

In each of Questions 21–24, y is a differentiable function of x. Choose the alternative that is the derivative

21. x³ − y³ = 1

(A) x

(B) 3x²

(C)

(D)

(E)

22. x + cos(x + y) = 0

(A) csc(x + y) − 1

(B) csc(x + y)

(C)

(D)

(E)

23. sin x − cos y − 2 = 0

(A) −cot x

(B) −cot y

(C)

(D) −csc y cos x

(E)

24. 3x² − 2xy + 5y² = 1

(A)

(B)

(C) 3x + 5y

(D)

(E) none of these

25. If x = t² + 1 and y = 2t³, then

(A) 3t

(B) 6t²

(C)

(D)

(E)

BC ONLY

26. If f (x) = x⁴ − 4x³ + 4x² − 1, then the set of values of x for which the derivative equals zero is

(A) {1,2}

(B) {0,−1,−2}

(C) {−1, + 2}

(D) {0}

(E) {0,1,2}

27. If f (x) = then f ″(4) is equal to

(A) −32

(B) −16

(C) −4

(D) −2

(E)

28. If f (x) = ln x³ then f ″(3) is

(A)

(B) −1

(C) −3

(D) 1

(E) none of these

29. If a point moves on the curve x² + y² = 25, then, at (0,5), is

(A) 0

(B)

(C) −5

(D)

(E) nonexistent

30. If x = t² − 1 and y = t⁴ − 2t³, then, when t = 1, is

(A) 1

(B) −1

(C) 0

(D) 3

(E)

BC ONLY

31. If f (x) = 5^x and 5^1.002 5.016, which is closest to f ′(1)?

(A) 0.016

(B) 1.0

(C) 5.0

(D) 8.0

(E) 32.0

32. If y = e^x (x − 1), then y ″(0) equals

(A) −2

(B) −1

(C) 0

(D) 1

(E) none of these

33. If x = e^θ cos θ and y = e^θ sin θ, then, when is

(A) 1

(B) 0

(C) e^π/2

(D) nonexistent

(E) −1

BC ONLY

34. If x = cos t and y = cos 2t, then is

(A) 4 cos t

(B) 4

(C)

(D) −4

(E) −4 cot t

BC ONLY

35.

(A) 0

(B) 1

(C) 6

(D) ∞

(E) nonexistent

36.

(A) 0

(B)

(C) 1

(D) 192

(E) ∞

37.

(A) 0

(B)

(C) 1

(D) e

(E) nonexistent

38.

(A) −1

(B) 0

(C) 1

(D) ∞

(E) none of these

39. 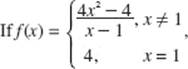which of these statements are true?

I. exists.

II. f is continuous at x = 1.

III. f is differentiable at x = 1.

(A) none

(B) I only

(C) I and II only

(D) I and III only

(E) I, II, and III

40. which of these statements are true?

I. exists.

II. g is continuous at x = 3.

III. g is differentiable at x = 3.

(A) I only

(B) II only

(C) III only

(D) I and II only

(E) I, II, and III

41. The function f (x) = x^2/3 on [−8, 8] does not satisfy the conditions of the Mean Value Theorem because

(A) f (0) is not defined

(B) f (x) is not continuous on [−8, 8]

(C) f ′(−1) does not exist

(D) f (x) is not defined for x < 0

(E) f ′(0) does not exist

42. If f (x) = 2x³ − 6x, at what point on the interval 0 ≤ x ≤ if any, is the tangent to the curve parallel to the secant line on that interval?

(A) 1

(B) −1

(C)

(D) 0

(E) nowhere

43. If h is the inverse function of f and if then h ′(3) =

(A) −9

(B)

(C)

(D) 3

(E) 9

44. equals

(A) 0

(B) 1

(C)

(D) ∞

(E) none of these

BC ONLY

45. If sin(xy) = x, then

(A) sec(xy)

(B)

(C)

(D)

(E) sec(xy) − 1

46.

(A) 1

(B) 2

(C)

(D) 0

(E) ∞

47.

(A) 1

(B)

(C)

(D) 0

(E) nonexistent

48.

(A) nonexistent

(B) 1

(C) 2

(D) ∞

(E) none of these

49.

(A)

(B) 0

(C) 1

(D) π

(E) ∞

50.

(A) is 1

(B) is 0

(C) is ∞

(D) oscillates between −1 and 1

(E) is none of these

51. The graph in the xy-plane represented by x = 3 + 2 sin t and y = 2 cos t − 1, for −π ≤ t ≤ π, is

(A) a semicircle

(B) a circle

(C) an ellipse

(D) half of an ellipse

(E) a hyperbola

BC ONLY

52. equals

(A) 0

(B)

(C) 1

(D) 2

(E) none of these

In each of Questions 53–56 a pair of equations that represent a curve parametrically is given. Choose the alternative that is the derivative

53. x = t − sin t and y = 1 − cos t

(A)

(B)

(C)

(D)

(E)

BC ONLY

54. x = cos³ θ and y = sin³ θ

(A) tan³ θ

(B) −cot θ

(C) cot θ

(D) −tan θ

(E) −tan² θ

BC ONLY

55. x = 1 − e^−t and y = t + e^−t

(A)

(B) e^−t − 1

(C) e^t + 1

(D) e^t − e^−2t

(E) e^t − 1

56. and y = 1 − ln(1 − t) (t < 1)

(A)

(B) t − 1

(C)

(D)

(E) 1 + ln x

Part B. Directions: Some of the following questions require the use of a graphing calculator.

In Questions 57–64, differentiable functions f and g have the values shown in the table.

57. If A = f + 2g, then A ′(3) =

(A) −2

(B) 2

(C) 7

(D) 8

(E) 10

58. If B = f · g, then B ′(2) =

(A) −20

(B) −7

(C) −6

(D) −1

(E) 13

59. If then D ′(1) =

(A)

(B)

(C)

(D)

(E)

60. If H(x) = then H ′(3) =

(A)

(B)

(C) 2

(D)

(E)

61. If K(x) = then K ′(0) =

(A)

(B)

(C)

(D)

(E)

62. If M(x) = f (g(x)), then M ′(1) =

(A) −12

(B) −6

(C) 4

(D) 6

(E) 12

63. If P(x) = f (x³), then P ′(1) =

(A) 2

(B) 6

(C) 8

(D) 12

(E) 54

64. If S(x) = f ⁻¹(x), then S ′(3) =

(A) −2

(B)

(C)

(D)

(E) 2

65. The graph of g ′ is shown here. Which of the following statements is (are) true of g at x = a ?

I. g is continuous.

II. g is differentiable.

III. g is increasing.

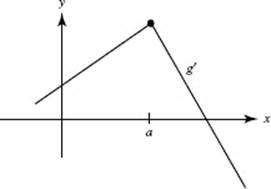
(A) I only

(B) III only

(C) I and III only

(D) II and III only

(E) I, II, and III

66. A function f has the derivative shown. Which of the following statements must be false?

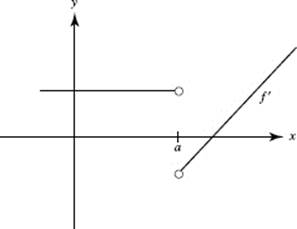
(A) f is continuous at x = a.

(B) f (a) = 0.

(C) f has a vertical asymptote at x = a.

(D) f has a jump discontinuity at x = a.

(E) f has a removable discontinuity at x = a.

67. The function f whose graph is shown has f ′ = 0 at x =

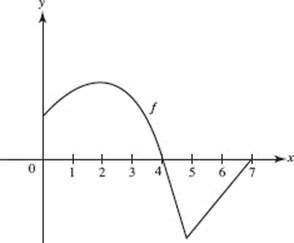
(A) 2 only

(B) 2 and 5

(C) 4 and 7

(D) 2, 4, and 7

(E) 2, 4, 5, and 7

68. A differentiable function f has the values shown. Estimate f ′(1.5).

(A) 8

(B) 12

(C) 18

(D) 40

(E) 80

69. Water is poured into a conical reservoir at a constant rate. If h(t) is the rate of change of the depth of the water, then h is

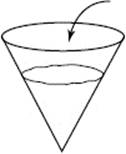
(A) constant

(B) linear and increasing

(C) linear and decreasing

(D) nonlinear and increasing

(E) nonlinear and decreasing

Use the figure to answer Questions 70–72. The graph of f consists of two line segments and a semicircle.

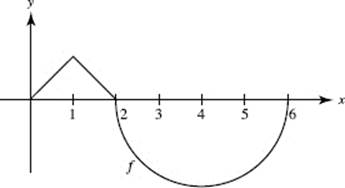
70. f ′(x) = 0 for x =

(A) 1 only

(B) 2 only

(C) 4 only

(D) 1 and 4

(E) 2 and 6

71. f ′(x) does not exist for x =

(A) 1 only

(B) 2 only

(C) 1 and 2

(D) 2 and 6

(E) 1, 2, and 6

72. f ′(5) =

(A)

(B)

(C) 1

(D) 2

(E)

73. At how many points on the interval [−5,5] is a tangent to y = x + cos x parallel to the secant line?

(A) none

(B) 1

(C) 2

(D) 3

(E) more than 3

74. From the values of f shown, estimate f ′(2).

(A) −0.10

(B) −0.20

(C) −5

(D) −10

(E) −25

75. Using the values shown in the table for Question 74, estimate (f ⁻¹) ′(4).

(A) −0.2

(B) −0.1

(C) −5

(D) −10

(E) −25

76. The “left half” of the parabola defined by y = x² − 8x + 10 for x ≤ 4 is a one-to-one function; therefore its inverse is also a function. Call that inverse g. Find g ′(3).

(A)

(B)

(C)

(D)

(E)

77. The table below shows some points on a function f that is both continuous and differentiable on the closed interval [2,10].

Which must be true?

(A) f (x) > 0 for 2 < x < 10

(B) f ′(6) = 0

(C) f ′(8) > 0

(D) The maximum value of f on the interval [2,10] is 30.

(E) For some value of x on the interval [2,10] f ′(x) = 0.

78. If f is differentiable and difference quotients overestimate the slope of f at x = a for all h > 0, which must be true?

(A) f ′(a) > 0

(B) f ′(a) < 0

(C) f ″(a) > 0

(D) f ″(a) < 0

(E) none of these

79. If f (u) = sin u and u = g(x) = x² − 9, then (f ° g) ′(3) equals

(A) 0

(B) 1

(C) 6

(D) 9

(E) none of these

80. If then the set of x’s for which f ′(x) exists is

(A) all reals

(B) all reals except x = 1 and x = −1

(C) all reals except x = −1

(D) all reals except and x = −1

(E) all reals except x = 1

81. If then the derivative of y² with respect to x² is

(A) 1

(B)

(C)

(D)

(E)

BC ONLY

82. If y = x² + x, then the derivative of y with respect to is

(A) (2x + 1)(x − 1)²

(B)

(C) 2x + 1

(D)

(E) none of these

BC ONLY

83. If and g(x) = then the derivative of f (g(x)) is

(A)

(B) −(x + 1)⁻²

(C)

(D)

(E)

84. If f (a) = f (b) = 0 and f (x) is continuous on [a, b], then

(A) f (x) must be identically zero

(B) f ′(x) may be different from zero for all x on [a, b]

(C) there exists at least one number c, a < c < b, such that f ′(c) = 0

(D) f ′(x) must exist for every x on (a, b)

(E) none of the preceding is true

85. Suppose y = f (x) = 2x³ − 3x. If h(x) is the inverse function of f, then h ′(−1) =

(A) −1

(B)

(C)

(D) 1

(E) 3

86. Suppose f (1) = 2, f ′(1) = 3, and f ′(2) = 4. Then (f ⁻¹) ′(2)

(A) equals

(B) equals

(C) equals

(D) equals

(E) cannot be determined

87. If f (x) = x³ − 3x² + 8x + 5 and g(x) = f ⁻¹(x), then g ′(5) =

(A) 8

(B)

(C) 1

(D)

(E) 53

88. Suppose It follows necessarily that

(A) g is not defined at x = 0

(B) g is not continuous at x = 0

(C) the limit of g(x) as x approaches 0 equals 1

(D) g ′(0) = 1

(E) g ′(1) = 0

Use this graph of y = f (x) for Questions 89 and 90.

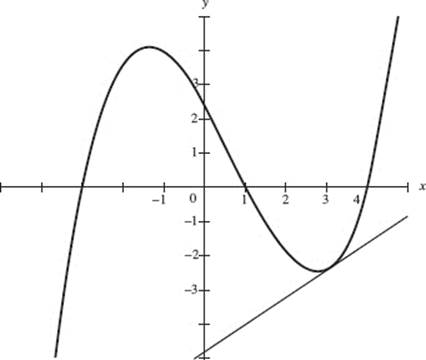
89. f ′(3) is most closely approximated by

(A) 0.3

(B) 0.8

(C) 1.5

(D) 1.8

(E) 2

90. The rate of change of f (x) is least at x

(A) −3

(B) −1.3

(C) 0

(D) 0.7

(E) 2.7

Use the following definition of the symmetric difference quotient for f ′ (x₀) for Questions 91–93: For small values of h,

91. For f (x) = 5^x, what is the estimate of f ′(2) obtained by using the symmetric difference quotient with h = 0.03?

(A) 25.029

(B) 40.236

(C) 40.252

(D) 41.223

(E) 80.503

92. To how many places is the symmetric difference quotient accurate when it is used to approximate f ′(0) for f (x) = 4^x and h = 0.08?

(A) 1

(B) 2

(C) 3

(D) 4

(E) more than 4

93. To how many places is f ′(x₀) accurate when it is used to approximate f ′(0) for f (x) = 4^x and h = 0.001?

(A) 1

(B) 2

(C) 3

(D) 4

(E) more than 4

94. The value of f ′(0) obtained using the symmetric difference quotient with f (x) = |x| and h = 0.001 is

(A) −1

(B) 0

(C) ±1

(D) 1

(E) indeterminate

95. If and h(x) = sin x, then equals

(A) g(sin x)

(B) cos x · g(x)

(C) g ′(x)

(D) cos x · g (sin x)

(E) sin x · g(sin x)

96. Let f (x) = 3^x − x³. The tangent to the curve is parallel to the secant through (0,1) and (3,0) for x =

(A) 0.984 only

(B) 1.244 only

(C) 2.727 only

(D) 0.984 and 2.804 only

(E) 1.244 and 2.727 only

Questions 97–101 are based on the following graph of f (x), sketched on −6 ≤ x ≤ 7. Assume the horizontal and vertical grid lines are equally spaced at unit intervals.

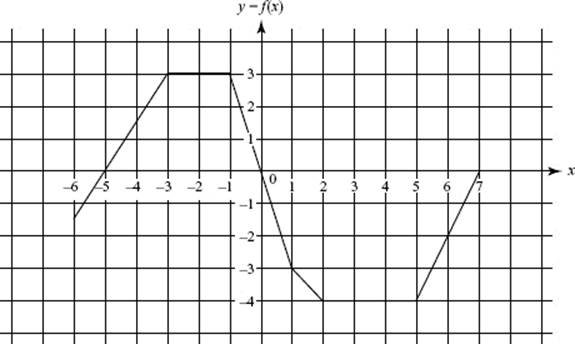
97. On the interval 1 < x < 2, f (x) equals

(A) −x − 2

(B) −x − 3

(C) −x − 4

(D) −x + 2

(E) x − 2

98. Over which of the following intervals does f ′(x) equal zero?

I. (−6,−3)

II. (−3,−1)

III. (2,5)

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) II and III only

99. How many points of discontinuity does f ′(x) have on the interval −6 < x < 7?

(A) none

(B) 2

(C) 3

(D) 4

(E) 5

100. For −6 < x < −3, f ′(x) equals

(A)

(B) −1

(C) 1

(D)

(E) 2

101. Which of the following statements about the graph of f ′(x) is false?

(A) It consists of six horizontal segments.

(B) It has four jump discontinuities.

(C) f ′(x) is discontinuous at each x in the set {−3,−1,1,2,5}.

(D) f ′(x) ranges from −3 to 2.

(E) On the interval −1 < x < 1, f ′(x) = −3.

102. The table gives the values of a function f that is differentiable on the interval [0,1]:

According to this table, the best approximation of f ′(0.10) is

(A) 0.12

(B) 1.08

(C) 1.17

(D) 1.77

(E) 2.88

103. At how many points on the interval [a, b] does the function graphed satisfy the Mean Value Theorem?

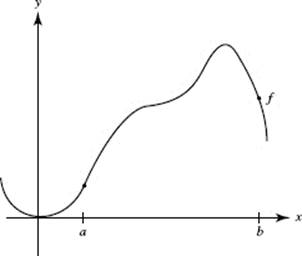
(A) none

(B) 1

(C) 2

(D) 3

(E) 4