Calculus AB and Calculus BC

CHAPTER 1 Functions

Concepts and Skills

In this chapter you will review precalculus topics. Although these topics are not directly tested on the AP exam, reviewing them will reinforce some basic principles:

• general properties of functions: domain, range, composition, inverse;

• special functions: absolute value, greatest integer; polynomial, rational, trigonometric, exponential, and logarithmic;

and the BC topics,

• parametrically defined curves • polar curves

Function

Domain

Range

A. DEFINITIONS

A1. A function f is a correspondence that associates with each element a of a set called the domain one and only one element b of a set called the range. We write

f (a) = b

to indicate that b is the value of f at a. The elements in the domain are called inputs, and those in the range are called outputs.

A function is often represented by an equation, a graph, or a table.

A vertical line cuts the graph of a function in at most one point.

EXAMPLE 1

The domain of f (x) = x² − 2 is the set of all real numbers; its range is the set of all reals greater than or equal to −2. Note that

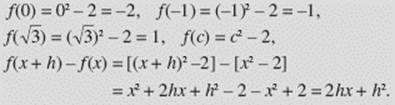
EXAMPLE 2

Find the domains of:

SOLUTIONS:

(a) The domain of is the set of all reals except x = 1 (which we shorten to “x ≠ 1”).

(b) The domain of

(c) The domain of is x 4, x ≠ 0 (which is a short way of writing {x | x is real, x < 0 or 0 < x 4}).

A2. Two functions f and g with the same domain may be combined to yield their sum and difference: f (x) + g(x) and f (x) − g(x), also written as (f + g) (x) and (f − g) (x), respectively; or their product and quotient: f (x)g(x) and f (x)/g(x), also written as (fg)(x) and (f/g) (x), respectively. The quotient is defined for all x in the shared domain except those values for which g(x), the denominator, equals zero.

EXAMPLE 3

If f (x) = x² − 4x and g(x) = x + 1, then find

SOLUTIONS: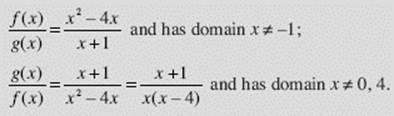

Composition

A3. The composition (or composite) of f with g, written as f (g(x)) and read as “f of g of x,” is the function obtained by replacing x wherever it occurs in f (x) by g(x). We also write (f ο g) (x) for f (g(x)). The domain of (f ο g) (x) is the set of all x in the domain of g for which g(x) is in the domain of f.

EXAMPLE 4A

If f (x) = 2x − 1 and g(x) = x², then does f (g(x)) = g(f (x))?

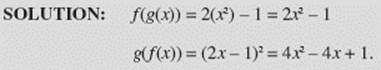
In general, f (g(x)) ≠ g(f (x)).

EXAMPLE 4B

If f (x) = 4x² − 1 and g(x) = find f (g(x)) and g(f (x)).

SOLUTIONS: f (g(x)) = 4x − 1 (x ≥ 0);

Symmetry

A4. A function f is if, for all x in the domain of f,

The graph of an odd function is symmetric about the origin; the graph of an even function is symmetric about the y-axis.

EXAMPLE 5

The graphs of x³ and g(x) = 3x² − 1 are shown in Figure N1–1; f (x) is odd, g(x) even.

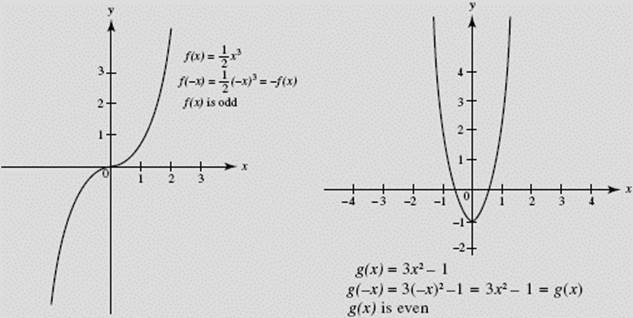
FIGURE N1–1

A5. If a function f yields a single output for each input and also yields a single input for every output, then f is said to be one-to-one. Geometrically, this means that any horizontal line cuts the graph of f in at most one point. The function sketched at the left in Figure N1–1 is one-to-one; the function sketched at the right is not. A function that is increasing (or decreasing) on an interval I is one-to-one on that interval.

A6. If f is one-to-one with domain X and range Y, then there is a function f ⁻¹, with domain Y and range X, such that

f ⁻¹(y₀) = x₀ if and only if f (x₀) = y₀.

The function f ⁻¹ is the inverse of f. It can be shown that f ⁻¹ is also one-to-one and that its inverse is f. The graphs of a function and its inverse are symmetric with respect to the line y = x.

EXAMPLE 6

Find the inverse of the one-to-one function f (x) = x³ − 1.

SOLUTION: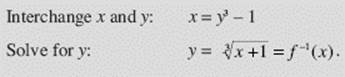

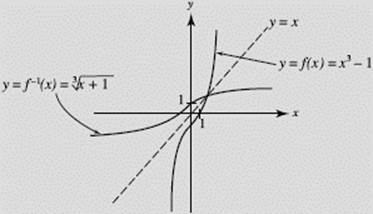
FIGURE N1–2

Note that the graphs of f and f ⁻¹ in Figure N1–2 are mirror images, with the line y = x as the mirror.

A7. The zeros of a function f are the values of x for which f (x) = 0; they are the x-intercepts of the graph of y = f (x).

EXAMPLE 7

Find zeros of f (x) = x⁴ − 2x².

SOLUTION: The zeros are the x’s for which x⁴ − 2x² = 0. The function has three zeros, since x⁴ − 2x² = x² (x² − 2) equals zero if x = 0, , or