Calculus AB and Calculus BC

CHAPTER 5 Antidifferentiation

Practice Exercises

Directions: Answer these questions without using your calculator.

1.

(A) x³ − x² + C

(B) 3x³ − x² + 3x + C

(C) x³ − x² + 3x + C

(D)

(E) none of these

2.

(A)

(B)

(C)

(D)

(E) none of these

3.

(A)

(B)

(C)

(D)

(E)

4.

(A)

(B)

(C)

(D)

(E) none of these

5.

(A)

(B)

(C)

(D)

(E)

6.

(A)

(B)

(C)

(D)

(E)

7.

(A)

(B)

(C) 2 ln|1 + 3u|+ C

(D)

(E) none of these

8.

(A)

(B)

(C)

(D)

(E)

9.

(A) 3 sin 3x + C

(B) −sin 3x + C

(C)

(D)

(E)

10.

(A)

(B)

(C)

(D)

(E)

11.

(A) tan⁻¹ (2x) + C

(B)

(C)

(D)

(E)

12.

(A)

(B)

(C)

(D)

(E)

13.

(A)

(B)

(C)

(D)

(E)

14.

(A)

(B)

(C)

(D)

(E)

15.

(A)

(B)

(C)

(D)

(E)

16.

(A)

(B)

(C) x + 2 ln |x| + C

(D) x + ln |2x| + C

(E)

17.

(A)

(B)

(C)

(D)

(E) none of these

18.

(A)

(B)

(C)

(D)

(E)

19.

(A) 3x^4/3 − 2x^5/2 − 2x^1/2 + C

(B) 3x^4/3 − 2x^5/2 + 2x^1/2 + C

(C)

(D)

(E) none of these

20.

(A)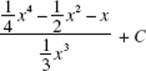

(B)

(C)

(D)

(E)

21.

(A)

(B)

(C)

(D)

(E)

22.

(A)

(B)

(C)

(D)

(E)

23.

(A)

(B)

(C)

(D)

(E) cos 2θ + C

24.

(A) −2 cos^1/2 x + C

(B)

(C)

(D)

(E)

25.

(A)

(B)

(C)

(D)

(E) none of these

26.

(A)

(B)

(C)

(D)

(E)

27.

(A)

(B) −2 cos 2θ + C

(C) −sin² θ + C

(D) cos² θ + C

(E)

28.

(A) x sin x + C

(B) x sin x + cos x + C

(C) x sin x − cos x + C

(D) cos x − x sin x + C

(E)

BC ONLY

29.

(A)

(B) tan 3u + C

(C)

(D)

(E)

30.

(A)

(B)

(C)

(D) ln |1 + sin x| + C

(E)

31.

(A) 2ln sin|θ − 1| + C

(B) −csc(θ − 1) + C

(C)

(D) − cot(θ − 1) + C

(E) csc (θ − 1) + C

32.

(A)

(B)

(C)

(D) ln |sec t + tan t| + C

(E)

33.

(A)

(B)

(C)

(D)

(E) 2 ln |sin x| + C

34.

(A)

(B)

(C) sec^3/2 x + C

(D)

(E) none of these

35.

(A) −ln|sec θ| + C

(B) sec² θ + C

(C) ln|sin θ| + C

(D) sec θ + C

(E) −ln|cos θ| + C

36.

(A)

(B)

(C)

(D) −cot x + C

(E) −csc 2x + C

37.

(A) sec⁻¹ y + C

(B) (tan⁻¹ y)² + C

(C) ln (1 + y²) + C

(D) ln (tan⁻¹ y) + C

(E) none of these

38.

(A)

(B)

(C) sin² θ cos θ + C

(D) cos³ θ + C

(E) none of these

39.

(A)

(B) −ln |1 − cos2t| + C

(C)

(D)

(E) 2 ln |1 − cos 2t| + C

40.

(A) ln |sin u| + C

(B)

(C)

(D) −sec 2u + C

(E) 2 ln |sin 2u| + C

41.

(A) x + ln |e^x − 1| + C

(B) x − e^x + C

(C)

(D)

(E) ln |e^x − 1| + C

42.

(A)

(B)

(C) ln|x − 2| + ln|x| + C

(D)

(E) none of these

BC ONLY

43.

(A)

(B) e^x2 (2x² + 1) + C

(C) 2e^x2 + C

(D) e^x2 + C

(E)

44.

(A) e^{sinθ + 1} + C

(B) e^{sin θ} + C

(C) −e^{sin θ} + C

(D) e^{cos θ} + C

(E) e^{sin θ} (cos θ − sin θ) + C

45.

(A) cos e^2θ + C

(B) 2e^4θ (cos e^2θ + sin e^2θ) + C

(C)

(D) −2 cos e^2θ + C

(E) none of these

46.

(A)

(B)

(C)

(D)

(E) none of these

47.

(A) e^−x (1 − x) + C

(B)

(C) −e^−x (x + 1) + C

(D)

(E) e^−x (x + 1) + C

BC ONLY

48.

(A) e^x (x² + 2x) + C

(B) e^x (x² − 2x − 2) + C

(C) e^x (x² − 2x + 2) + C

(D) e^x (x − 1)² + C

(E) e^x (x + 1)² + C

BC ONLY

49.

(A) x − ln|e^x − e^−x | + C

(B) x + 2 ln|e^x − e^−x | + C

(C)

(D) ln|e^x − e^−x | + C

(E) ln (e^x + e^−x) + C

50.

(A) tan⁻¹ e^x + C

(B)

(C) ln (1 + e^2x) + C

(D)

(E) 2 tan⁻¹ e^x + C

51.

(A) ln|ln v| + C

(B)

(C)

(D) 2 ln v + C

(E)

52.

(A)

(B) ln² x + C

(C)

(D)

(E)

53.

(A) x² (3 ln x + 1) + C

(B)

(C)

(D)

(E) none of these

BC ONLY

54.

(A)

(B) (ln − 1) + C

(C)

(D) ln ( − 1) + C

(E) ln + + C

BC ONLY

55.

(A)

(B) 3x (ln x − 1) + C

(C) 3 ln x(x − 1) + C

(D)

(E) none of these

BC ONLY

56.

(A)

(B)

(C)

(D)

(E)

BC ONLY

57.

(A)

(B)

(C) −ln|ln v| + C

(D)

(E) ln|ln v| + C

BC ONLY

58.

(A) y − 2 ln|y + 1| + C

(B)

(C)

(D) 1 − 2 ln |y + 1| + C

(E)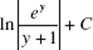

59.

(A) ln (x² + 2x + 2) + C

(B) ln |x + 1| + C

(C) arctan(x + 1) + C

(D)

(E)

60.

(A) 2(x^3/2 − x) + C

(B)

(C)

(D)

(E)

61.

(A) e^θ (cos θ − sin θ) + C

(B) e^θ sin θ + C

(C)

(D) 2 e^θ (sin θ + cos θ) + C

(E)

BC ONLY

62.

(A)

(B) ln t − 2 ln² t + ln³ t + C

(C) −2(1 − ln t) + C

(D)

(E)

63.

(A) u tan u + ln|cos u| + C

(B)

(C)

(D) u tan u − ln|sin u| + C

(E) u sec u − ln|sec u + tan u| + C

BC ONLY

64.

(A) ln (x² + 4) + C

(B)

(C)

(D)

(E) none of these

65.

(A)

(B) sin⁻¹ x + C

(C)

(D)

(E)

66.

(A)

(B) sin⁻¹ (1 − 2x) + C

(C)

(D)

(E)

67.

(A) tan⁻¹ e^x + C

(B) e^x − ln (1 + e^x) + C

(C) e^x − x + ln|1 + e^x | + C

(D)

(E) none of these

68.

(A) sec θ tan θ + C

(B) sin θ − csc θ + C

(C) ln (1 + sin² θ) + C

(D) tan⁻¹ (sin θ) + C

(E)

69.

(A) arc tan x + C

(B) x arc tan x − ln (1 + x²) + C

(C) x arc tan x + ln (1 + x²) + C

(D)

(E)

BC ONLY

70.

(A) −ln|1 − e^x | + C

(B) x − ln|1 − e^x | + C

(C)

(D) e^−x ln |1 + e^x | + C

(E) none of these

71.

(A)

(B)

(C) ln |y| − y + 2y² + C

(D)

(E) none of these

72.

(A)

(B) e^u3/3 + C

(C)

(D)

(E) e^{1 + 2 lnu} + C

73.

(A)

(B)

(C)

(D) tan⁻¹ (ln|y|) + C

(E) none of these

74.

(A) sec θ + θ + 2 ln|cosθ| + C

(B) tan θ + 2 ln|cos θ| + C

(C) tan θ − 2 sec² θ + C

(D) sec θ + θ − tan² θ + C

(E) tan θ − 2 ln|cosθ| + C

75.

(A) sec θ − tan θ + C

(B) ln (1 + sin θ) + C

(C) ln |sec θ + tan θ| + C

(D) θ + ln|csc θ − cot θ| + C

(E) none of these

76. A particle starting at rest at t = 0 moves along a line so that its acceleration at time t is 12t ft/sec². How much distance does the particle cover during the first 3 sec?

(A) 16 ft

(B) 32 ft

(C) 48 ft

(D) 54 ft

(E) 108 ft

77. The equation of the curve whose slope at point (x, y) is x² − 2 and which contains the point (1, −3) is

(A)

(B) y = 2x − 1

(C)

(D)

(E) 3y = x³ − 10

78. A particle moves along a line with acceleration 2 + 6t at time t. When t = 0, its velocity equals 3 and it is at position s = 2. When t = 1, it is at position s =

(A) 2

(B) 5

(C) 6

(D) 7

(E) 8

79. Find the acceleration (in ft/sec²) needed to bring a particle moving with a velocity of 75 ft/sec to a stop in 5 sec.

(A) −3

(B) −6

(C) −15

(D) −25

(E) −30

80.

(A)

(B) ln|x² − 1| + C

(C) x + tan⁻¹ x + C

(D)

(E)

BC ONLY