Calculus AB and Calculus BC

CHAPTER 6 Definite Integrals

C. INTEGRALS INVOLVING PARAMETRICALLY DEFINED FUNCTIONS

The techniques are illustrated in Examples 22 and 23.

BC ONLY

EXAMPLE 22

Evaluate where x = 2 sin θ and y = 2 cos θ.

SOLUTION: Note that dx = 2 cos θ dθ, that when x = −2, and that when x = 2.

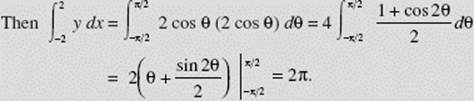
When using parametric equations we must be sure to express everything in terms of the parameter. In Example 22 we replaced in terms of θ: (1) the integrand, (2) dx, and (3) both limits. Remember that we have defined dx as x ′(θ) dθ.

EXAMPLE 23

Express xy dx in terms of t if x = ln t and y = t³.

SOLUTION:

We see that We now find limits of integration in terms of t:

For x = 0, we solve ln t = 0 to get t = 1.

For x = 1, we solve ln t = 1 to get t = e.