Calculus AB and Calculus BC
CHAPTER 7 Applications of Integration to Geometry
Practice Exercises
Part A. Directions: Answer these questions without using your calculator.
AREA
In Questions 1–11, choose the alternative that gives the area of the region whose boundaries are given.
1. The curve of y = x2, y = 0, x = −1, and x = 2.
(A) 
(B) 
(C) 3
(D) 5
(E) none of these
2. The parabola y = x2 − 3 and the line y = 1.
(A) 
(B) 32
(C) 
(D) 
(E) none of these
3. The curve of x = y2 − 1 and the y-axis.
(A) 
(B) 
(C) 
(D) 
(E) none of these
4. The parabola y2 = x and the line x + y = 2.
(A) 
(B) 
(C) 
(D) 
(E) 
5. The curve of 
the x-axis, and the vertical lines x = −2 and x = 2.
(A) 
(B) 
(C) 2π
(D) π
(E) none of these
6. The parabolas x = y2 − 5y and x = 3y − y2.
(A) 
(B) 
(C) 
(D) 
(E) none of these
7. The curve of 
and x + y = 3.
(A) 
(B) 
(C) 
(D) 
(E) 
8. In the first quadrant, bounded below by the x-axis and above by the curves of y = sin x and y = cos x.
(A) 
(B) 
(C) 2
(D) 
(E) 
9. Bounded above by the curve y = sin x and below by y = cos x from 
(A) 
(B) 
(C) 
(D) 
(E) 
10. The curve y = cot x, the line 
and the x-axis.
(A) ln 2
(B) 
(C) 1
(D) 
(E) 2
11. The curve of y = x3 − 2x2 − 3x and the x-axis.
(A) 
(B) 
(C) 
(D) 
(E) none of these
12. The total area bounded by the cubic x = y3 − y and the line x = 3y is equal to
(A) 4
(B) 
(C) 8
(D) 
(E) 16
13. The area bounded by y = ex, y = 2, and the y-axis is equal to
(A) 3 − e
(B) e2 − 1
(C) e2 + 1
(D) 2 ln 2 − 1
(E) 2 ln 2 − 3
14. The area enclosed by the ellipse with parametric equations x = 2 cos θ and y = 3 sin θ equals
(A) 6π
(B) 
(C) 3π
(D) 
(E) none of these
BC ONLY
15. The area enclosed by one arch of the cycloid with parametric equations x = θ − sin θ and y = 1 − cos θ equals
(A) 
(B) 3π
(C) 2π
(D) 6π
(E) none of these
BC ONLY
16. The area enclosed by the curve y2 = x(1 − x) is given by
(A) 
(B) 
(C) 
(D) π
(E) 2π
BC ONLY
17. The figure below shows part of the curve of y = x3 and a rectangle with two vertices at (0,0) and (c, 0). What is the ratio of the area of the rectangle to the shaded part of it above the cubic?
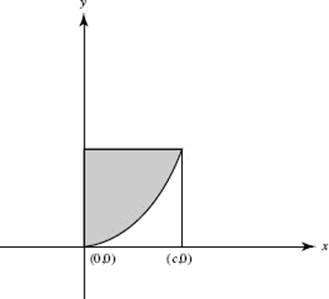
(A) 3:4
(B) 5:4
(C) 4:3
(D) 3:1
(E) 2:1
VOLUME
In Questions 18–24 the region whose boundaries are given is rotated about the line indicated. Choose the alternative that gives the volume of the solid generated.
18. y = x2, x = 2, and y = 0; about the x-axis.
(A) 
(B) 8π
(C) 
(D) 
(E) 
19. y = x2, x = 2, and y = 0; about the y-axis.
(A) 
(B) 4π
(C) 
(D) 8π
(E)
20. The first quadrant region bounded by y = x2, the y-axis, and y = 4; about the y-axis.
(A) 8π
(B) 4π
(C) 
(D) 
(E) 
21. y = x2 and y = 4; about the x-axis.
(A) 
(B) 
(C) 
(D) 
(E) none of these
22. y = x2 and y = 4; about the line y = 4.
(A) 
(B) 
(C) 
(D) 
(E)
23. An arch of y = sin x and the x-axis; about the x-axis.
(A) 
(B) 
(C) 
(D) π2
(E) π(π − 1)
24. A trapezoid with vertices at (2,0), (2, 2), (4,0), and (4,4); about the x-axis.
(A) 
(B) 
(C) 
(D) 
(E) none of these
25. The base of a solid is a circle of radius a, and every plane section perpendicular to a diameter is a square. The solid has volume
(A) 
(B) 2πa3
(C) 4πa3
(D) 
(E) 
26. The base of a solid is the region bounded by the parabola x2 = 8y and the line y = 4, and each plane section perpendicular to the y-axis is an equilateral triangle. The volume of the solid is
(A) 
(B) 
(C) 
(D) 32
(E) none of these
27. The base of a solid is the region bounded by y = e−x, the x-axis, the y-axis, and the line x = 1. Each cross section perpendicular to the x-axis is a square. The volume of the solid is
(A) 
(B) e2 − 1
(C) 
(D) 
(E) 
ARC LENGTH
28. The length of the arc of the curve y2 = x3 cut off by the line x = 4 is
(A) 
(B) 
(C) 
(D) 
(E) none of these
BC ONLY
29. The length of the arc of y = ln cos x from 
equals
(A) 
(B) 2
(C) 
(D) 
(E) 
BC ONLY
IMPROPER INTEGRALS
30. 
(A) 1
(B) 
(C) −1
(D) 
(E) none of these
31. 
(A) 1
(B)
(C) 
(D) −1
(E) none of these
32. 
(A) 
(B) 
(C) 3
(D) 1
(E) none of these
33. 
(A) 6
(B) 
(C)
(D) 0
(E) none of these
34. 
(A) 2
(B) −2
(C) 0
(D)
(E) none of these
35. 
(A) −2
(B)
(C) 2
(D)
(E) none of these
BC ONLY
In Questions 36–40, choose the alternative that gives the area, if it exists, of the region described.
36. In the first quadrant under the curve of y = e−x.
(A) 1
(B) e
(C) 
(D) 2
(E) none of these
37. In the first quadrant under the curve of y = xe−x2.
(A) 2
(B) 
(C)
(D) 
(E) none of these
38. In the first quadrant above y = 1, between the y-axis and the curve xy = 1.
(A) 1
(B) 2
(C)
(D) 4
(E) none of these
39. Between the curve 
and the x-axis.
(A) 2π
(B) 4π
(C) 8π
(D) π
(E) none of these
40. Above the x-axis, between the curve 
and its asymptotes.
(A) 
(B) π
(C) 2π
(D) 4π
(E) none of these
In Questions 41 and 42, choose the alternative that gives the volume, if it exists, of the solid generated.
41. 
at the left by x = 1, and below by y = 0; about the x-axis.
(A) 
(B) π
(C) 2π
(D) 4π
(E) none of these
42. The first-quadrant region under y = e−x ; about the x-axis.
(A)
(B) π
(C) 2π
(D) 4π
(E) none of these
Part B. Directions: Some of the following questions require the use of a graphing calculator.
AREA
In Questions 43–47, choose the alternative that gives the area of the region whose boundaries are given.
43. The area bounded by the parabola y = 2 − x2 and the line y = x − 4 is given by
(A) 
(B) 
(C) 
(D) 
(E) none of these
BC ONLY
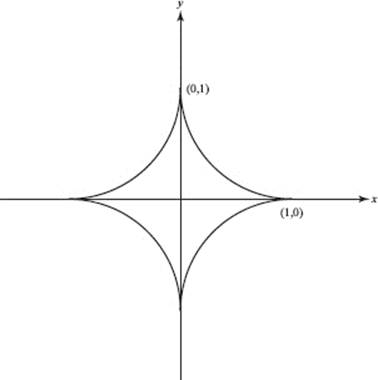
44. The area enclosed by the hypocycloid with parametric equations x = cos3 t and y = sin3 t as shown in the above diagram is
(A) 
(B) 
(C) 
(D) 
(E) none of these
BC ONLY
45. Suppose the following is a table of ordinates for y = f (x), given that f is continuous on [1, 5]:
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
1.62 |
4.15 |
7.5 |
9.0 |
12.13 |
If a trapezoid sum in used, with n = 4, then the area under the curve, from x = 1 to x = 5, is equal, to two decimal places, to
(A) 6.88
(B) 13.76
(C) 20.30
(D) 25.73
(E) 27.53
46. The area A enclosed by the four-leaved rose r = cos 2θ equals, to three decimal places,
(A) 0.785
(B) 1.571
(C) 2.071
(D) 3.142
(E) 6.283
BC ONLY
47. The area bounded by the small loop of the limaçon r = 1 − 2 sin θ is given by the definite integral
(A) 
(B) 
(C) 
(D) 
(E) 
BC ONLY
VOLUME
In Questions 48–54 the region whose boundaries are given is rotated about the line indicated. Choose the alternative that gives the volume of the solid generated.
48. y = x2 and y = 4; about the line y = −1.
(A) 
(B) 
(C) 
(D) 
(E) none of these
49. y = 3x − x2 and y = 0; about the x-axis.
(A) 
(B) 
(C) 
(D) 
(E) 
50. y = 3x − x2 and y = x; about the x-axis.
(A) 
(B) 
(C) 
(D) 
(E) 
51. y = ln x, y = 0, x = e; about the line x = e.
(A) 
(B) 
(C) 
(D) 
(E) none of these
52. The curve with parametric equations x = tan θ, y = cos2 θ, and the lines x = 0, x = 1, and y = 0; about the x-axis.
(A) 
(B) 
(C) 
(D) 
(E) 
BC ONLY
53. A sphere of radius r is divided into two parts by a plane at distance h (0 < h < r) from the center. The volume of the smaller part equals
(A) 
(B) 
(C) 
(D) 
(E) none of these
CHALLENGE
54. If the curves of f (x) and g(x) intersect for x = a and x = b and if f (x) > g(x) > 0 for all x on (a, b), then the volume obtained when the region bounded by the curves is rotated about the x-axis is equal to
(A) 
(B) 
(C) 
(D) 
(E) none of these
ARC LENGTH
55. The length of one arch of the cycloid 
equals
(A) 
(B) 
(C) 
(D) 
(E) 
BC ONLY
56. The length of the arc of the parabola 4x = y2 cut off by the line x = 2 is given by the integral
(A) 
(B) 
(C) 
(D) 
(E) none of these
BC ONLY
57. The length of x = et cos t, y = et sin t from t = 2 to t = 3 is equal to
(A) 
(B) 
(C) 2(e3 − e2)
(D) e3 (cos 3 + sin 3) − e2 (cos 2 + sin 2)
(E) none of these
CHALLENGE
IMPROPER INTEGRALS
58. Which one of the following is an improper integral?
(A) 
(B) 
(C) 
(D) 
(E) none of these
59. Which one of the following improper integrals diverges?
(A) 
(B) 
(C) 
(D) 
(E) none of these
60. Which one of the following improper integrals diverges?
(A) 
(B) 
(C) 
(D) 
(E) 