Calculus AB and Calculus BC

CHAPTER 1 Functions

D. TRIGONOMETRIC FUNCTIONS

The fundamental trigonometric identities, graphs, and reduction formulas are given in the Appendix.

D1. Periodicity and Amplitude.

The trigonometric functions are periodic. A function f is periodic if there is a positive number p such that f (x + p) = f (x) for each x in the domain of f. The smallest such p is called the period of f. The graph of f repeats every p units along the x-axis. The functions sin x, cos x, csc x, and sec xhave period 2π; tan x and cot x have period π.

The function f (x) = A sin bx has amplitude A and period g(x) = tan cx has period

EXAMPLE 10

Consider the function f (x) = cos (kx).

(a) For what value of k does f have period 2?

(b) What is the amplitude of f for this k ?

SOLUTIONS:

(a) Function f has period since this must equal 2, we solve the equation getting k = π.

(b) It follows that the amplitude of f that equals has a value of

EXAMPLE 11

Consider the function

Find (a) the period and (b) the maximum value of f.

(c) What is the smallest positive x for which f is a maximum?

(d) Sketch the graph.

SOLUTIONS:

(a) The period of f is or 6.

(b) Since the maximum value of −sin x is −(−1) or +1, the maximum value of f is 3 + 1 or 4.

(c) equals +1 when that is, when Solving yields

(d) We graph in [−5,8] × [0,5]:

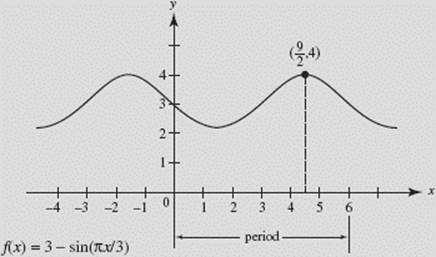
FIGURE N1–6

D2. Inverses.

Inverse trig functions

We obtain inverses of the trigonometric functions by limiting the domains of the latter so each trigonometric function is one-to-one over its restricted domain. For example, we restrict

The graphs of f (x) = sin x on and of its inverse f ⁻¹(x) = sin⁻¹ x are shown in Figure N1–7. The inverse trigonometric function sin⁻¹ x is also commonly denoted by arcsin x, which denotes the angle whose sine is x. The graph of sin⁻¹ x is, of course, the reflection of the graph of sin x in the line y = x.

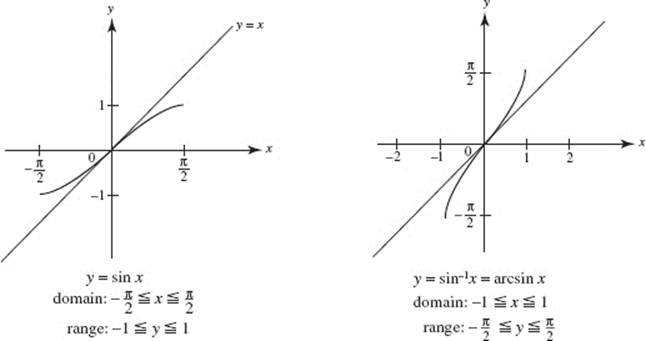
FIGURE N1–7

Also, for other inverse trigonometric functions,

y = cos⁻¹ x (or arccos x) has domain −1 x 1 and range 0 y π;

y = tan⁻¹ x (or arctan x) has domain the set of reals and range

Note also that