Calculus AB and Calculus BC

AB Practice Examination 1

SECTION I

Part A TIME: 55 MINUTES

The use of calculators is not permitted for this part of the examination. There are 28 questions in Part A, for which 55 minutes are allowed. Because there is no deduction for wrong answers, you should answer every question, even if you need to guess.

Directions: Choose the best answer for each question.

1.

(A) −5

(B) ∞

(C) 0

(D) 5

(E) 1

2.

(A) 0

(B) ln 2

(C)

(D)

(E) ∞

3. If y = e^−x2, then y ″ (0) equals

(A) 2

(B) −2

(C)

(D) 0

(E) −4

Questions 4 and 5. Use the following table, which shows the values of the differentiable functions f and g.

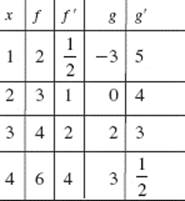
4. The average rate of change of function f on [1,4] is

(A) 7/6

(B) 4/3

(C) 15/8

(D) 9/4

(E) 8/3

5. If h(x) = g(f (x)) then h ′(3) =

(A) 1/2

(B) 1

(C) 4

(D) 6

(E) 9

6. The derivative of a function f is given for all x by

f ′(x) = x²(x + 1)³(x − 4)².

The set of x values for which f is a relative maximum is

(A) {0, −1, 4}

(B) {−1}

(C) {0,4}

(D) {1}

(E) none of these

7. If equals

(A)

(B)

(C)

(D)

(E)

8. The maximum value of the function f (x) = xe ^−x is

(A)

(B) e

(C) 1

(D) −1

(E) none of these

9. Which equation has the slope field shown below?

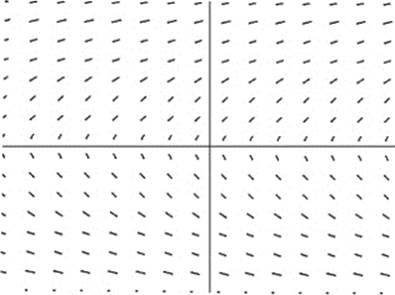
(A)

(B)

(C)

(D)

(E)

Questions 10–12. The graph below shows the velocity of an object moving along a line, for 0 ≤ t ≤ 9.

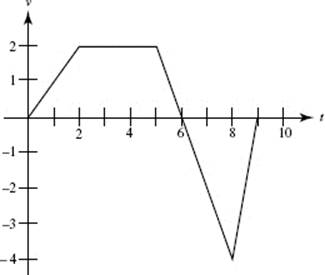
10. At what time does the object attain its maximum acceleration?

(A) 2 < t < 5

(B) 5 < t < 8

(C) t = 6

(D) t = 8

(E) 8 < t < 9

11. The object is farthest from the starting point at t =

(A) 2

(B) 5

(C) 6

(D) 8

(E) 9

12. At t = 8, the object was at position x = 10. At t = 5, the object’s position was x =

(A) −5

(B) 5

(C) 7

(D) 13

(E) 15

13. α cos α dα is equal to

(A)

(B)

(C)

(D)

(E)

14. equals

(A) 3 ln (e − 3)

(B) 1

(C)

(D)

(E) none of these

15. A differentiable function has the values shown in this table:

Estimate f ′(2.1).

(A) 0.34

(B) 0.59

(C) 1.56

(D) 1.70

(E) 1.91

16. If A = is approximated using Riemann sums and the same number of subdivisions, and if L, R, and T denote, respectively left, right, and trapezoid sums, then it follows that

(A) R ≤ A ≤ T ≤ L

(B) R ≤ T ≤ A ≤ L

(C) L ≤ T ≤ A ≤ R

(D) L ≤ A ≤ T ≤ R

(E) None of these is true.

17. The number of vertical tangents to the graph of y² = x − x³ is

(A) 4

(B) 3

(C) 2

(D) 1

(E) 0

18.

(A)

(B)

(C)

(D)

(E)

19. The equation of the curve shown below is What does the area of the shaded region equal?

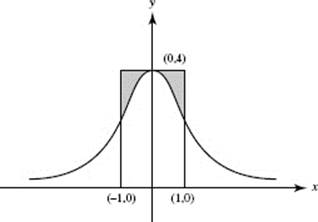
(A)

(B) 8 − 2π

(C) 8 − π

(D)

(E) 2π − 4

20. Over the interval 0 ≤ x ≤ 10, the average value of the function f shown below

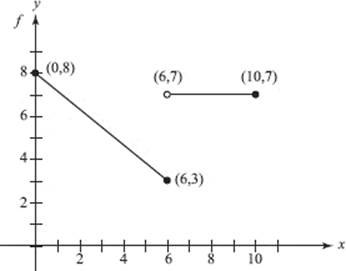
(A) is 6.00.

(B) is 6.10.

(C) is 6.25.

(D) does not exist, because f is not continuous.

(E) does not exist, because f is not integrable.

21. If f ′(x) = 2f (x) and f (2) = 1, then f (x) =

(A) e^{2x − 4}

(B) e^2x + 1 − e⁴

(C) e^4−2x

(D) e^{2x + 1}

(E) e^{x − 2}

22. The table below shows values of f ″(x) for various values of x:

The function f could be

(A) a linear function

(B) a quadratic function

(C) a cubic function

(D) a fourth-degree function

(E) an exponential function

23. The curve x³ + x tan y = 27 passes through (3,0). Use the tangent line there to estimate the value of y at x = 3.1. The value is

(A) −2.7

(B) −0.9

(C) 0

(D) 0.1

(E) 3.0

24. At what value of h is the rate of increase of twice the rate of increase of h ?

(A)

(B)

(C) 1

(D) 2

(E) 4

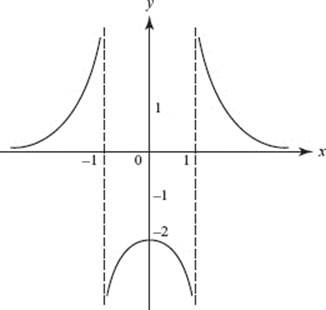
25. The graph of a function y = f (x) is shown above. Which is true?

(A)

(B)

(C)

(D)

(E)

26. A function f (x) equals for all x except x = 1. For the function to be continuous at x = 1, the value of f (1) must be

(A) 0

(B) 1

(C) 2

(D) ∞

(E) none of these

27. The number of inflection points on the graph of f (x) = 3x⁵ − 10x³ is

(A) 4

(B) 3

(C) 2

(D) 1

(E) 0

28. Suppose It follows that

(A) f increases for all x

(B) f increases only if x < −4

(C) f has a local min at x = −4

(D) f has a local max at x = −4

(E) f has no critical points

Part B TIME: 50 MINUTES

Some questions in this part of the examination require the use of a graphing calculator. There are 17 questions in Part B, for which 50 minutes are allowed. Because there is no deduction for wrong answers, you should answer every question, even if you need to guess.

Directions: Choose the best answer for each question. If the exact numerical value of the correct answer is not listed as a choice, select the choice that is closest to the exact numerical answer.

29. Let G(x) = [f (x)]². At x = a, the graph of f is increasing and concave downward, while G is decreasing. Which describes the graph of G at x = a ?

(A) concave downward

(B) concave upward

(C) linear

(D) point of inflection

(E) none of these

30. The value of c for which has a local minimum at x = 3 is

(A) −9

(B) −6

(C) −3

(D) 6

(E) 9

31. An object moving along a line has velocity v (t) = t cos t − ln (t + 2), where 0 ≤ t ≤ 10. The object achieves its maximum speed when t is approximately

(A) 3.7

(B) 5.1

(C) 6.4

(D) 7.6

(E) 9.5

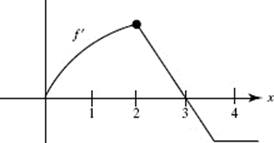
32. The graph of f ′, which consists of a quarter-circle and two line segments, is shown above. At x = 2, which of the following statements is true?

(A) f is not continuous.

(B) f is continuous but not differentiable.

(C) f has a relative maximum.

(D) The graph of f has a point of inflection.

(E) none of these

33. Let where f is the function whose graph appears below.

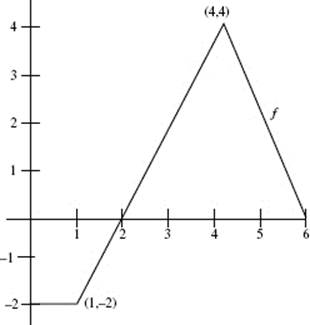
The local linearization of H(x) near x = 3 is H(x)

(A) −2x + 8

(B) 2x − 4

(C) −2x + 4

(D) 2x − 8

(E) 2x − 2

34. The table shows the speed of an object, in feet per second, at various times during a 12-second interval.

Estimate the distance the object travels, using the midpoint method with 3 subintervals.

(A) 100 ft

(B) 101 ft

(C) 111 ft

(D) 112 ft

(E) 150 ft

35. In a marathon, when the winner crosses the finish line many runners are still on the course, some quite far behind. If the density of runners x miles from the finish line is given by R(x) = 20[1 − cos(1 + 0.03x²)] runners per mile, how many are within 8 miles of the finish line?

(A) 30

(B) 145

(C) 157

(D) 166

(E) 195

36. Which best describes the behavior of the function at x = 1?

(A) It has a jump discontinuity.

(B) It has an infinite discontinuity.

(C) It has a removable discontinuity.

(D) It is both continuous and differentiable.

(E) It is continuous but not differentiable.

37. If then f ′(t) equals

(A)

(B)

(C)

(D)

(E) tan⁻¹ t²

38.

(A)

(B)

(C)

(D)

(E)

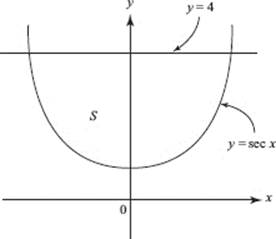
39. The region S in the figure shown above is bounded by y = sec x and y = 4. What is the volume of the solid formed when S is rotated about the x-axis?

(A) 0.304

(B) 39.867

(C) 53.126

(D) 54.088

(E) 108.177

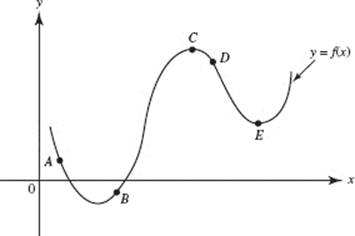
40. At which point on the graph of y = f (x) shown above is f ′(x) < 0 and f ″(x) > 0?

(A) A

(B) B

(C) C

(D) D

(E) E

41. Let f (x) = x⁵ + 1, and let g be the inverse function of f. What is the value of g ′(0)?

(A) −1

(B)

(C) 1

(D) g ′(0) does not exist.

(E) g ′(0) cannot be determined from the given information.

42. The hypotenuse AB of a right triangle ABC is 5 feet, and one leg, AC, is decreasing at the rate of 2 feet per second. The rate, in square feet per second, at which the area is changing when AC = 3 is

(A)

(B)

(C)

(D)

(E)

43. At how many points on the interval [0,π] does f (x) = 2 sin x + sin 4x satisfy the Mean Value Theorem?

(A) none

(B) 1

(C) 2

(D) 3

(E) 4

44. If the radius r of a sphere is increasing at a constant rate, then the rate of increase of the volume of the sphere is

(A) constant

(B) increasing

(C) decreasing

(D) increasing for r < 1 and decreasing for r > 1

(E) decreasing for r < 1 and increasing for r > 1

45. The rate at which a purification process can remove contaminants from a tank of water is proportional to the amount of contaminant remaining. If 20% of the contaminant can be removed during the first minute of the process and 98% must be removed to make the water safe, approximately how long will the decontamination process take?

(A) 2 min

(B) 5 min

(C) 18 min

(D) 20 min

(E) 40 min

SECTION II

Part A TIME: 30 MINUTES
2 PROBLEMS

A graphing calculator is required for some of these problems.
See instructions

1. A function f is defined on the interval [0,4], and its derivative is f ′(x) = e^{sin x} − 2 cos 3x.

(a) Sketch f ′ in the window [0,4] × [−2,5].

(Note that the following questions refer to f.)

(b) On what interval is f increasing? Justify your answer.

(c) At what value(s) of x does f have local maxima? Justify your answer.

(d) How many points of inflection does the graph of f have? Justify your answer.

2. The rate of sales of a new software product is given by S(t), where S is measured in hundreds of units per month and t is measured in months from the initial release date of January 1, 2012. The software company recorded these sales data:

(a) Using a trapezoidal approximation, estimate the number of units the company sold during the second quarter (April 1, 2012, through June 30, 2012).

(b) After looking at these sales figures, a manager suggests that the rate of sales can be modeled by assuming the rate to be initially 120 units/month and to double every 3 months. Write an equation for S based on this model.

(c) Compare the model’s prediction for total second quarter sales with your estimate from part a.

(d) Use the model to predict the average value of S(t) for the entire first year. Explain what your answer means.

Part B TIME: 60 MINUTES
4 PROBLEMS

No calculator is allowed for any of these problems.
If you finish Part B before time has expired, you may return to work on Part A, but you may not use a calculator.

3. The graph of function y = f (x) passes through point (2, 5) and satisfies the differential equation

(a) Write an equation of the line tangent to f at (2, 5).

(b) Using this tangent line, estimate f (2.1).

(c) Solve the differential equation, expressing f as a function of x.

(d) Using your answer to part (c), find f (2.1).

4. Let R represent the first-quadrant region bounded by the y-axis and the curves y = 2^x and as shown in the graph.

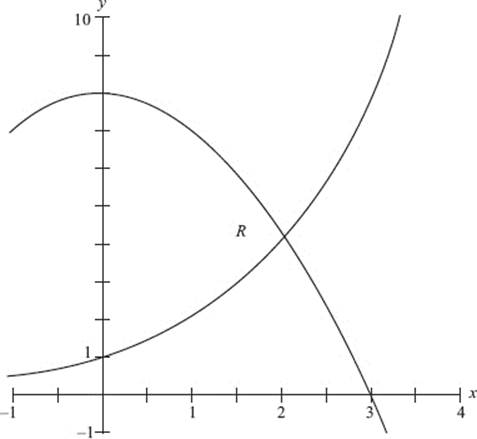
(a) Find the area of region R.

(b) Set up, but do not evaluate, integrals in terms of a single variable for:

(i) the volume of the solid formed when R is rotated around the x-axis,

(ii) the volume of the solid whose base is R, if all cross sections in planes perpendicular to the x-axis are squares.

5. Given the function f (x) = e^2x(x² − 2):

(a) For what values of x is f decreasing?

(b) Does this decreasing arc reach a local or a global minimum? Justify your answer.

(c) Does f have a global maximum? Justify your answer.

6. (a) A spherical snowball melts so that its surface area shrinks at the constant rate of 10 square centimeters per minute. What is the rate of change of volume when the snowball is 12 centimeters in diameter?

(b) The snowball is packed most densely nearest the center. Suppose that, when it is 12 centimeters in diameter, its density x centimeters from the center is given by grams per cubic centimeter. Set up an integral for the total number of grams (mass) of the snowball then. Do not evaluate.